Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
The king wants to marry off his daughter. Three suitors apply -- a logician, politician and a lawyer. The king may ask two of them a yes/no question, for which the suitor must know the answer. The logician always tells the truth. The politician always lies. The lawyer says either randomly. The three men know each other. The king seeks only to avoid choosing the lawyer for his daughter. What question should he ask of the two suitors?
Here is something easier.
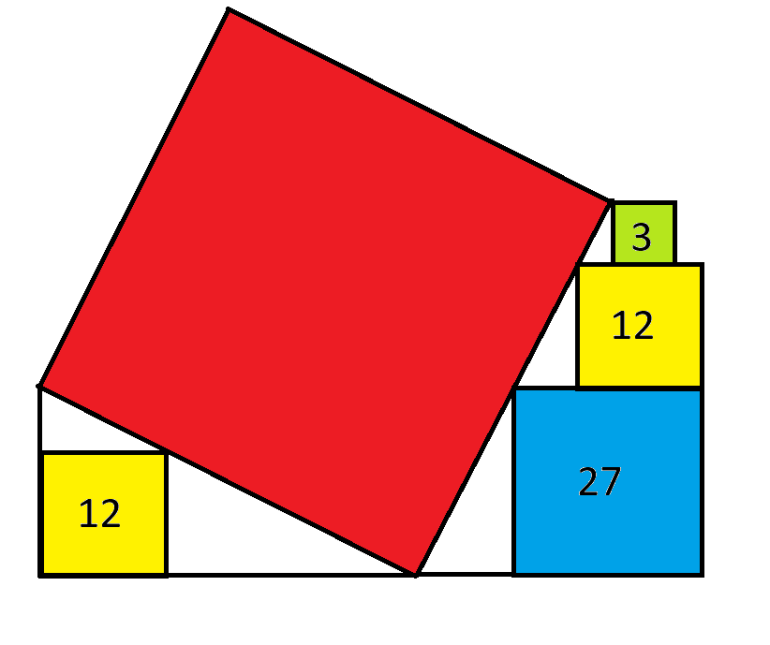
Find the area of the red square.
You don't need the yellow square on the left. In fact, a harder problem might have been to calculate that square's area.
The lengths of the sides of the squares on the right are: green, sqrt(3); yellow, 2 sqrt(3); blue, 3 sqrt(3)
The three white triangles formed by the red square and the three other squares are similar.
Since the white triangle next to the yellow square has height 2 sqrt(3) and base length (3 sqrt(3) - 2 sqrt(3)) = sqrt(3), its hypotenuse is sqrt(15).
Since the white triangles are similar, and the height of the top one = 1/2 the height of the middle one, the hypotenuse of the top one = 1/2 the hypotenuse of the middle one = sqrt(15) / 2.
Also, since the height of the bottom one = 3/2 the height of the middle one, the hypotenuse of the middle one = 3/2 the hypotenuse of the middle one = 3/2 sqrt(15).
The length of the side of the red square = the sum of the lengths of the hypotenuses of the three white triangles = 3 sqrt(15), so the area is the square of that, or 135.
Assumption - all coloured boxes are square.
Solution:
Let the length of the side of the red square = x.
The length of the sides of the green, yellow and blue boxes are the sq. root of their respective areas.
Green Box: sq. root 3
Yellow Box: sq. root 12 = 2* sq. root 3
Blue Box: sq. root 27 = 3* sq. root 3
By deduction the base lengths of the three white triangles are:
Green Box: (sq. root 3)/2
Yellow Box: sq. root 3
Blue Box: 1.5*(sq. root 3)
The sum of the lengths of the hypotenuses of the three triangles equals the length of the side of the red square.
x = sq. root[(6*sq. root 3)² + (3*sq. root 3)²]
= sq. root 135
The area of the red square is 135 sq. units.
Not exactly a math puzzle, but here goes!
In a standard game of Monopoly:
1. How can you go bankrupt by bankrupting another player?
2. How can you legally avoid going bankrupt in that situation?
Here is a link to a PDF with the Monopoly rules:
https://www.hasbro.com/common/instruct/monins.pdf
Dog Hand
P.S. My favorite Monopoly token is, naturally, the dog.
Quote: WizardI love Monopoly, but I don't quite understand what you're asking.
link to original post
Wiz,
I am asking under what circumstances when you bankrupt a player, you yourself also go bankrupt immediately.
Dog Hand
However I think the puzzle uses the rule that when you go bankrupt you hand everything over, including mortgaged properties, and the receiver now has to pay 10% or unmortgage those, and thus also goes bankrupt. This can probably only happen with Player B owning Old Kent Road and Player A having mortgaged Mayfair, and neither player has money. Player A must have drawn the "Return to Old Kent Road" card (otherwise would have £200). Player A hasn't passed Go to get there but has to pay £2. Player B receives mortgaged Mayfair but can't raise the £40, even by mortgaging Old Kent Road; so also goes bankrupt.
As Player B, your correct tactic should have been to mortgage Old Kent Road at the end of the last move.
Quote: charliepatrickI can't remember all the cards you can draw but there used to be one where you got $10/£10 from every player. So It's possible you can bankrupt a player from your move.
However I think the puzzle uses the rule that when you go bankrupt you hand everything over, including mortgaged properties, and the receiver now has to pay 10% or unmortgage those, and thus also goes bankrupt. This can probably only happen with Player B owning Old Kent Road and Player A having mortgaged Mayfair, and neither player has money. Player A must have drawn the "Return to Old Kent Road" card (otherwise would have £200). Player A hasn't passed Go to get there but has to pay £2. Player B receives mortgaged Mayfair but can't raise the £40, even by mortgaging Old Kent Road; so also goes bankrupt.
As Player B, your correct tactic should have been to mortgage Old Kent Road at the end of the last move.
link to original post
Ding! Full credit for first question, but only partial credit for the second.
Dog Hand
Thanks - I had forgotten about the second question.Quote: DogHand...Ding! Full credit for first question, but only partial credit for the second...
Quote: charliepatrickThanks - I had forgotten about the second question.Quote: DogHand...Ding! Full credit for first question, but only partial credit for the second...
You could always fail to ask for the rent, although the rules are ambiguous if you own the set (the other property would already have been mortgaged in this case), or you could just mortgage Old Kent Road "at any time", say just after the dice had been rolled/card picked and shown, but before any movement.
link to original post
Ding! Ding! We have a winner.
Well done, charliepatrick.
Dog Hand
What is the expected number of rolls of a 6-sided die needed before a 6 is rolled, if you only consider sets of rolls where all of the numbers are even?
Clarification:
If you roll a 2, then a 5, you ignore both of those rolls and "start over." A sequence of 2, 5, 4, 4, 6 counts as a single sequence of 3 rolls (4, 4, 6), not of 5 rolls.
"Well, since you are ignoring sets of rolls with odd numbers, and each even number has a 1/3 chance of being rolled each time, this is the same as the expected number of rolls of a 3-sided die with 2, 4, and 6 on the sides, which is 3."
First, determine the expected number using the original probabilities:
P(1 roll) = 1/6
P(2 rolls) = 1/3 x 1/6, since the first roll must be 2 or 4
P(3 rolls) = (1/3)^2 x 1/6, since the first two rolls must be 2 or 4
...
P(n rolls) = (1/3)^(n-1) x 1/6
The expected number = 1 x 1/6 + 2 x 1/3 x 1/6 + 3 x (1/3)^2 x 1/6 + ...
= 1/6 x (1 + 2 x 1/3 + 3 x (1/3)^2 + ...)
= 1/6 x (1 + 1/3 + (1/3)^2 + ...)^2
Now, calculate the probability that one of these actually happened
This is 1/6 x (1 + 1/3 + (1/3)^2 + ...)
Divide the first by the second to get the actual expected number
This is (1 + 1/3 + (1/3)^2 + ...) = 3/2
On the front: "On the back of this shirt is a true statement."
On the back: "On the front of this shirt is a false statement."
Which sides were true?

Quote: WizardIn the movie Saturday Night, the character of George Carlin wears a shirt that says as follows:
On the front: "On the back of this shirt is a true statement."
On the back: "On the front of this shirt is a false statement."
Which sides were true?
link to original post
The in-side. George Carlin probably never lied to us.
Quote: AutomaticMonkeyQuote: WizardIn the movie Saturday Night, the character of George Carlin wears a shirt that says as follows:
On the front: "On the back of this shirt is a true statement."
On the back: "On the front of this shirt is a false statement."
Which sides were true?
link to original post
The in-side. George Carlin probably never lied to us.
link to original post
For all we know, the inside had the statement, "This statement is false."
- 4 - 10 = 9 - 15
- Add 25/4 to each side: 4 - 10 + 25/4 = 9 - 15 + 25/4
- Factor both sides: (2 - 5/2)^2 = (3-5/2)^2
- Take square root of both sides: (2 - 5/2) = (3-5/2)
- Add 5/2 to both sides: 2 = 3
Where is the error?
Quote: ThatDonGuyIn step 4: a^2 = b^2 does not imply a = b. Otherwise, x = -x for all real x.
link to original post
I agree.
To be honest this is more of a, can you write a simple program to work it out, as I couldn't see a "simple" trial and error method. (I did see a manual method but felt it would take too long.)
You have to pick all different digits from 1-9, say A B C D E and F, and work out SQRT(ABC)-SQRT(DE)-SQRT(F) to be as close to zero as possible.
The answer I got was 0.xxx xxx 789 383 679 669... where, by coincidence xxx xxx was a square!
Quote: charliepatrickI saw this puzzle on facebook, but by the time I looked at it, I couldn't get back to the puzzle to see if my answer was theirs.
To be honest this is more of a, can you write a simple program to work it out, as I couldn't see a "simple" trial and error method. (I did see a manual method but felt it would take too long.)
You have to pick all different digits from 1-9, say A B C D E and F, and work out SQRT(ABC)-SQRT(DE)-SQRT(F) to be as close to zero as possible.
The answer I got was 0.xxx xxx 789 383 679 669... where, by coincidence xxx xxx was a square!
link to original post
I get the same answer with brute force computing:
Quote: WizardNew Question! I bolded the differences from the previous one.
The king wants to marry off his daughter. Three suitors apply -- a logician, politician and a lawyer. The king may ask two of them a yes/no question, for which the suitor must know the answer. The logician always tells the truth. The politician always lies. The lawyer says either randomly. The three men know each other. The king seeks only to avoid choosing the lawyer for his daughter. What question should he ask of the two suitors?
link to original post
ďIf I asked you ĎIs the other man the lawyer?í would you say yes?Ē
1) The game starts by Alan putting one bullet in the revolver, spinning the cylinder, putting the gun to his head and then pulling the trigger once. After that (assuming Alan survives), the game can continue in any format. A player's turn can consist of any number of spins, pulls or bullets
2) There must be between one and five bullets in the revolver at all times
3) Game decisions are made by a player pulling the trigger with the gun to his own head. There are no other ways to use the gun (or any other device) as a randomizer
4) When a player makes a pull, there must be >0 probability of survival
5) First player to shoot himself loses. Surviving player wins
Problem: Format the game so that Alan and Bob have an even chance of winning
After Alan's first turn, add a second bullet. From this point on, there will always be two bullets in the gun, and each turn consists of a spin and pull.
The probability that Alan wins is 5/6 (the probability of not shooting himself on the first turn) times the sum of:
1/3 (Bob shoots himself)
(2/3)^2 x 1/3 (both players draw empty chambers, then Bob shoots himself)
(2/3)^4 x 1/3 (both players draw empty chambers twice, then Bob shoots himself)
(2/3)^6 x 1/3 (both players draw empty chambers three times, then Bob shoots himself)
...
This is 5/6 x 1/3 x (1 + 4/9 + (4/9)^2 + (4/9)^3 + ...)
= 5/18 x (1 / (1 - 4/9))
= 5/18 x 9/5
= 1/2.
Quote: ThatDonGuy
After Alan's first turn, add a second bullet. From this point on, there will always be two bullets in the gun, and each turn consists of a spin and pull.
The probability that Alan wins is 5/6 (the probability of not shooting himself on the first turn) times the sum of:
1/3 (Bob shoots himself)
(2/3)^2 x 1/3 (both players draw empty chambers, then Bob shoots himself)
(2/3)^4 x 1/3 (both players draw empty chambers twice, then Bob shoots himself)
(2/3)^6 x 1/3 (both players draw empty chambers three times, then Bob shoots himself)
...
This is 5/6 x 1/3 x (1 + 4/9 + (4/9)^2 + (4/9)^3 + ...)
= 5/18 x (1 / (1 - 4/9))
= 5/18 x 9/5
= 1/2.
link to original post
I agree with that answer
There are many solutions to this problem. So far I've come up with
1) After making first pull with one bullet in chamber, Alan pulls again without respinning. Then it's Bob's turn...with three bullets in he spins once and pulls once. Then game restarts. Note: pulling twice with one bullet (no respin) is same chance of survival as pulling once with two bullets in
2) Alan spins and makes first pull with one bullet. The gun then passes from player to player who each make one pull without respinning. Technically this format can continue to sixth pull and be fair, but for sixth pull it's no longer a game since Bob would have 100% chance of death. Therefore, the game must restart after either the second pull or the fourth pull
These are both very simple solutions since the probability of winning is even after only two iterations.
1. Two bullets are put in the chamber in consecutive positions.
2. Chamber is spun.
3. Alan pulls.
4. If Alan survives he pulls again.
5. If he still survives, he passes the gun to Bob who must pull four more times without spinning, ensuring Bob loses.
Quote: WizardMaybe this violates the rules but here is my answer.
1. Two bullets are put in the chamber in consecutive positions.
2. Chamber is spun.
3. Alan pulls.
4. If Alan survives he pulls again.
5. If he still survives, he passes the gun to Bob who must pull four more times without spinning, ensuring Bob loses.
link to original post
Rule #1 is that Alan starts with one bullet in cylinder, then spins and pulls. So you canít start the game with two bullets in the cylinder
Rule #4 is that every pull must have a >0 chance of survival. Ensuring a player loses is not allowed
Incidentally, there is no way Bob could pull four times since his death is guaranteed after three pulls using your format
Quote: Ace2
...Rule #4 is that every pull must have a >0 chance of survival. Ensuring a player loses is not allowed
Incidentally, there is no way Bob could pull four times since his death is guaranteed after three pulls using your format
link to original post
That's a little ambiguous to me being a handgun shot to the head is only 90% fatal. So even if the gun fires there is still a >0 chance of survival.
Alan makes first spin/pull with one bullet
Bob adds two bullets, spins, then pulls once
Alan adds one more bullet, spins, then pulls once
Then the game continues like that with Bob making a single spin/pull with three bullets in cylinder and Alan making a single pull/spin with four bullets in the cylinder
Alanís chance of winning is 5/6 * 1/2 * ((1/6)^0 + (1/6)^1 + (1/6)^2Ö.) = 1/2
The logician always tells the truth.
The politician always lies.
The lawyer lies or tells the truth randomly.
They make the following statements:
Alex: Charlie is the politician.
Bob: Alex is the logician.
Charlie: I am the lawyer.
Who has what profession?
Quote: WizardAlex, Bob and Charlie are, in no particular order, a logician, politician and lawyer.
The logician always tells the truth.
The politician always lies.
The lawyer lies or tells the truth randomly.
The make the following statements:
Alex: Charlie is the politician.
Bob: Alex is the logician.
Charlies: I am the lawyer.
Who has what profession?
link to original post
Assuming Charles and Charlie are the same person...
Thus, Alex's statement is true, Charles' is false, and Bob's is true.
Dog Hand
Therefore, Alex is the logician, which means "Charlie is the politician" is true.
Alex is the logician; Bob is the lawyer; Charlie is the politician
Check:
Alex's "Charlie is the politician" is true
Charlie's "I am the lawyer" is false
A bat and a ball cost $1.10 in total. The bat costs $1.00 more than the ball. How much does the ball cost?
I got it wrong.
Quote: MichaelBluejayFrom CNBC.
A bat and a ball cost $1.10 in total. The bat costs $1.00 more than the ball. How much does the ball cost?
I got it wrong.If the ball costs 10 cents, then the bat would cost $1.10, which would bring the total to $1.20. The correct answer is the ball costs 5 cents and the bat $1.05.
link to original post
Let "ball" be the price of the ball in cents
Ball + (Ball + 100) = 110
2 Ball = 10, so the ball costs 5 cents and the bat costs $1.05
Quote: MichaelBluejayFrom CNBC.
A bat and a ball cost $1.10 in total. The bat costs $1.00 more than the ball. How much does the ball cost?
I got it wrong.
this is why we always use equations.

since ball is x, then ball is 0.05. bat is 1+x, so bat is 1.05.
check:
1+x+x = 1.1
1+0.05+0.05 = 1.1 ✓
What's the price of a ball in dollars?
Assume prices can be stated to any number of decimal places. For full credit, you must answer the problem without doing any calculations
Let phi = 1 / ball; phi - 1 = 1 / phi
The only number that is 1 more than its reciprocal is the "golden ratio" of (sqrt(5) + 1) / 2 (not coincidentally, usually represented by the Greek letter phi), so the price of the ball is 2 / (sqrt(5) + 1) = (sqrt(5) - 1) / 2.
Quote: Ace2The price of a used bat at Goodwill is $1. The price of a bat divided by the price of a ball is equal to the total price of a bat & ball divided by the price of a bat
What's the price of a ball in dollars?
Assume prices can be stated to any number of decimal places. For full credit, you must answer the problem without doing any calculations
link to original post
I donít see the path to full credit
To answer without calculations, you should recognize that the price ratios are the golden ratio(Φ): bat to ball is the same as total to bat. Knowing that you can give the answer as:
Φ - 1 dollars
Alan and Bob decide to play Russian Roulette using a revolver with six chambers. Rules:
- There must be between one and five bullets in the revolver at all times.
- The gun must pass back and forth after every pull of the trigger.
Problem: Format the game so that Alan and Bob have an even chance of winning
Use any format you like. Flip a fair coin to determine who goes firstQuote: WizardHere is an easy variant of Ace2's Russian roulette puzzle.
Alan and Bob decide to play Russian Roulette using a revolver with six chambers. Rules:
- There must be between one and five bullets in the revolver at all times.
- The gun must pass back and forth after every turn.
Problem: Format the game so that Alan and Bob have an even chance of winning
link to original post
Quote: WizardHere is an easy variant of Ace2's Russian roulette puzzle.
Alan and Bob decide to play Russian Roulette using a revolver with six chambers. Rules:
- There must be between one and five bullets in the revolver at all times.
- The gun must pass back and forth after every turn.
Problem: Format the game so that Alan and Bob have an even chance of winning
link to original post
I think my answer to Ace2's version applies here as well
Assuming you're a $100 flat bettor, what's your total expected wager on this hand?
Quote: Ace2Use any format you like. Flip a fair coin to determine who goes first
link to original post
I think it was implied other randomization methods are not allowed.
Quote: Ace2Playing blackjack, you are dealt a pair of 2s against a dealer 3. You play basic strategy which means you split 2s and double down with 9-11 against a dealer 3. This is an infinite deck game with no limit on resplitting or doubles
Assuming you're a $100 flat bettor, what's your total expected wager on this hand?
link to original post
Note: edited 4/8/25 6:41 AM


