Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
[[{(38/18)^(5+1) - 1} / {(38/18) - 1}] - 1] / 2 =~ 38.9 spins
Quote: ThatDonGuyQuote: WizardWhat is the expected number of spins in double-zero roulette to see five reds or five blacks in a row? The previous spin landed on 0.
link to original post
Let E(n) be the expected number after having n consecutive of a color; E(5) = 0
Let p be the probability of getting a particular color, and r = 1 - 2p = the probability that it comes up green
E(4) = 1 + p E(1) + r E(0)
E(3) = 1 + p E(1) + r E(0) + p E(4)
= 1 + p E(1) + r E(0) + p (1 + p E(1) + r E(0))
= 1 + p + (p + p^2) E(1) + (r + pr) E(0)
E(2) = 1 + p E(1) + r E(0) + p E(3)
= 1 + p E(1) + r E(0) + p (1 + p + (p + p^2) E(1) + (r + pr) E(0))
= (1 + p + p^2) + p (1 + p + p^2) E(1) + r (1 + p + p^2) E(0)
E(1) = 1 + p E(1) + r E(0) + p E(3)
= (1 + p + p^2 + p^3) + p (1 + p + p^2 + p^3) E(1) + r (1 + p + p^2 + p^3) E(0)
(1 - p - p^2 - p^3 - p^4) E(1) = (1 + p + p^2 + p^3) + (1 - 2p) (1 + p + p^2 + p^3) E(0)
E(1) = (1 + p + p^2 + p^3) / (1 - p - p^2 - p^3 - p^4) + ((1 - 2p) (1 + p + p^2 + p^3) / (1 - p - p^2 - p^3 - p^4)) E(0)
E(0) = 1 + (1 - 2p) E(0) + 2p E(1)
E(0) = 1 / 2p + E(1)
E(0) = 1 / 2p + (1 + p + p^2 + p^3) / (1 - p - p^2 - p^3 - p^4) + ((1 - 2p) (1 + p + p^2 + p^3) / (1 - p - p^2 - p^3 - p^4)) E(0)
(1 - (1 - 2p) (1 + p + p^2 + p^3) / (1 - p - p^2 - p^3 - p^4)) E(0) = 1 / 2p + (1 + p + p^2 + p^3) / (1 - p - p^2 - p^3 - p^4)
E(0) = (1 / 2p + (1 + p + p^2 + p^3) / (1 - p - p^2 - p^3 - p^4)) x (1 - p - p^2 - p^3 - p^4) / p^4
E(0) = (1 - p - p^2 - p^3 - p^4) / (2 p^5) + (1 + p + p^2 + p^3) / p^4
E(0) = (1 - p - p^2 - p^3 - p^4) / (2 p^5) + (2p + 2p^2 + 2p^3 + 2p^4) / (2p^5)
= (1 + p + p^2 + p^3 + p^4) / (2p^5)
= (1 - p^5) / (2 p^5 (1 - p))
For p = 9/19, this is 4,592,395 / 118,098, or about 38.8863
link to original post
I agree! That one is beer worthy.
Eliot's approximation was correct to the four significant digits given. Of course, an exact expression is required for the beer.
Ace is also correct and extra credit for the formula for n spins.
The answer is, of course, (36/38)*(18/38)^4*(20/38) = 0.025103 or 1-in-39.836. I find it odd that this is even close to the other question Mike asked (the expected number of spins to get a sequence Red or Black of length 5). I was almost going to go with 39.836 as my answer.
With the last spin being zero, the chance of getting five black or five red in the next five spins is (18/38)^5 * 2 or about 1 in 21. Not close to the answerQuote: teliotWhat I finds odd about this problem is this related problem: what are the chances that starting with the present spin you get a sequence of exactly 5 reds or 5 blacks?
The answer is, of course, (36/38)*(18/38)^4*(20/38) = 0.025103 or 1-in-39.836. I find it odd that this is even close to the other question Mike asked (the expected number of spins to get a sequence Red or Black of length 5). I was almost going to go with 39.836 as my answer.
link to original post
Look at it this way. The chance of you getting two consecutive heads in the next two rolls is 1 in 4, but the expected waiting time to see two consecutive heads is six. Red/black is not much different from heads/tails…would be identical without those dang two zeroes on the wheel
I'm just saying that two unrelated questions about five in a row have surprisingly close answers.
Mathematician 1 gets 1% of the cake.
Mathematician 2 gets 2% of the remaining cake.
Mathematician 3 gets 3% of the remaining cake.
Mathematician 4 gets 4% of the remaining cake.
This continues until the last mathematician gets 100% of what is left.
Which mathematician gets the most cake?
No calculators allowed!
For full credit, I need an explanation why your answer is right.
I also hate to keep saying this, but please don't just throw out a link to a video that solves the problem *ahem*. Let's have some fun and try to learn something.
When N=10 the 10th person gets 10% and the 11th person get 11% of 90% = 9.9%. Similarly the 9th person gets 9% and the 10th person gets 10% of 91% = 9.1%. Confirming the 10th person gets the most.
Quote: charliepatrickPerson N gets N/100 of what's left. In which case person (N+1) gets (N+1)/100*(100-N)/100. This means 100N=100N+100-N2-N which means N2+N-100=0. Using N=-b2+/-SQRT(etc) gives -1+-SQRT(1+400)/2 which is about 10.
When N=10 the 10th person gets 10% and the 11th person get 11% of 90% = 9.9%. Similarly the 9th person gets 9% and the 10th person gets 10% of 91% = 9.1%. Confirming the 10th person gets the most.
link to original post
Agreed. Full credit for a similar solution as mine.
𝗻𝘂𝗺𝗯𝗲𝗿 𝟵, 𝗻𝘂𝗺𝗯𝗲𝗿 𝟵, 𝗻𝘂𝗺𝗯𝗲𝗿 𝟵, 𝗻𝘂𝗺𝗯𝗲𝗿 𝟵, 𝗻𝘂𝗺𝗯𝗲𝗿 𝟵___________________that is part of the lyrics from the Beatles song "Revolution"
the 9 times mystery:
at least it's a mystery to me..............I'm sure some here can explain it - an easy puzzle I'm sure for some - but not for me
I haven't got a clue
nothing similar happens with any other digits that I know about
here we go:
9*5=45.......................add up the digits - 4+5=9
9*8=72.......................add up the digits - 7+2=9
9*7=63.......................add up the digits - 6+3=9
9*17=153...................add up the digits - 1+5+3 =9
9*77=693...................add up the digits - 6+9+3 and get 18............then add up those digits..............1+8=9
9*4,796=43,164..........add up the digits 4+3+1+6+4 and get 18......then add up those digits...............1+8=9
9*104,675 = 942,075.........add up the digits..........9+4+2+0+7+5 and get 27...........then add up those digits..............2+7=9
9*5,327,894 = 47,951,046...........add up the digits .........4+7+9+5+1+0+4+6 and get 36............then add up those digits.................3+6=9
𝗻𝘂𝗺𝗯𝗲𝗿 𝟵, 𝗻𝘂𝗺𝗯𝗲𝗿 𝟵, 𝗻𝘂𝗺𝗯𝗲𝗿 𝟵, 𝗻𝘂𝗺𝗯𝗲𝗿 𝟵, 𝗻𝘂𝗺𝗯𝗲𝗿 𝟵
.
For two digits numbers the number can be expressed as 10a+b, where as the total of the digits is a+b. This if a+b=9, then 9a+a+b is also a multiple of 9, and this is 10a+b.
For three digits use 100a+10b+c and observe that 99a+9b+(a+b+c) is also divisible by 9 if (a+b+c) is. If a+b+c is greater than 9 then repeat the process, and note the same logic applies for the number formed by a+b+c.
For larger numbers you can see that each power of 10 can be considered as (99..99+1) so the number breaks down to 9*something+(a+b+.....+z). So you can see the pattern applies for all numbers.
btw the same applies to numbers divisible by 3, the total wil always reduce to 3 6 or 9.
It takes Alice and Cindy 4 hours to paint a house.
It takes Bill and Cindy 5 hours to paint a house.
How long does it take if they all paint?
Quote: WizardIt takes Alice and Bill 3 hours to paint a house.
It takes Alice and Cindy 4 hours to paint a house.
It takes Bill and Cindy 5 hours to paint a house.
How long does it take if they all paint?
link to original post
Let A, B, and C be the amount of the house Alice, Bill, and Cindy can paint in an hour
A + B = 1/3
A + C = 1/4
B + C = 1/5
2 (A + B + C) = 1/3 + 1/4 + 1/5 = 47/60
A + B + C = 47/120
It takes all three 120/47, or 2 26/47, hours
Quote: WizardIt takes Alice and Bill 3 hours to paint a house.
It takes Alice and Cindy 4 hours to paint a house.
It takes Bill and Cindy 5 hours to paint a house.
How long does it take if they all paint?
link to original post
3A+3B=4A+4C=5B+5C=size of house
3A=2B+5C
4A=5B+C
8B+20C=15B+3C
17C=7B
Let B=17 C=7 gives A=23
This has A+B=40, A+C=30, B+C=24
So if this is how many rooms they can each paint, then the house has 120 rooms.
So the time for all of them to paint house is 120/47 = 2h33:11.489s
Quote: ThatDonGuy
Let A, B, and C be the amount of the house Alice, Bill, and Cindy can paint in an hour
A + B = 1/3
A + C = 1/4
B + C = 1/5
2 (A + B + C) = 1/3 + 1/4 + 1/5 = 47/60
A + B + C = 47/120
It takes all three 120/47, or 2 26/47, hours
link to original post
I agree! Charlie was right too, but five minutes behind you.
It takes Alice 3 hours to paint a house.
It takes Bill 4 hours to paint a house.
It takes Cindy 5 hours to paint a house.
How long does it take if they all paint?
Also, I hope I can hire any of them at a normal hourly rate for a painter, because their throughput is phenomenal.
Flip the triangle upside-down by moving only 3 balls.
⬤⬤⬤⬤
⬤⬤⬤
⬤⬤
⬤
Then move the single ball at the bottom to the very top.
Quote: MichaelBluejayHow about a variant?
It takes Alice 3 hours to paint a house.
It takes Bill 4 hours to paint a house.
It takes Cindy 5 hours to paint a house.
How long does it take if they all paint?
Also, I hope I can hire any of them at a normal hourly rate for a painter, because their throughput is phenomenal.
link to original post
In one hour, Alice paints 1/3 of a house, Bill paints 1/4 of a house, and Cindy paints 1/5 of a house
Togethger, they paint 1/3 + 1/4 + 1/5 = 47 / 60 of a house in an hour.
They can paint one house in 60 / 47 hours
Quote: MichaelBluejayThis is from my local weekly newspaper's math column. I didn't get this one, because I'm not good with spatial concepts.
Flip the triangle upside-down by moving only 3 balls.⬤⬤⬤⬤
⬤⬤⬤
⬤⬤
⬤Move the top-left and top-right balls down to the row of 2, making it a row of 4.
Then move the single ball at the bottom to the very top.
link to original post
This solution is a little confusing. To be clearer, I would say, move the top-left and top-right balls 2 rows down making it the bottom row.
Move top row, two on left to 3rd row left.
Move bottom to new top row on right.
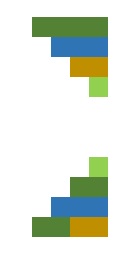
That wouldn't be clearer, because it would be wrong. The two balls move down to the penultimate row, not the bottom row.Quote: acesideThis solution is a little confusing. To be clearer, I would say, move the top-left and top-right balls 2 rows down making it the bottom row.
Also, you've revealed part of the solution outside the spoiler, but I guess the ball is out of the bag now.
Quote: MichaelBluejayThis is from my local weekly newspaper's math column. I didn't get this one, because I'm not good with spatial concepts.
Flip the triangle upside-down by moving only 3 balls.⬤⬤⬤⬤
⬤⬤⬤
⬤⬤
⬤
link to original post
Here is another way of putting the solution.
The color-coding is exceptionally clear.Quote: WizardHere is another way of putting the solution.
I was sitting in a local cafe earlier this week and noticed that all the chairs were either red, black or white. Also each table had four seats. It got me thinking if all the tables had been circular (i.e. a seating arrangement RRBW is the same as RBWR etc.) and every table had four chairs with a different arrangement from any other table, what would be the largest possibe cafe size.
In other words how many possible ways are there to arrange four chairs, each being either Red, Black or White, around a circular table.
I think it's fair to say that the answer is bigger than the number of tables my local cafe actually has!!
Quote: charliepatrickSeats in a Cafe
I was sitting in a local cafe earlier this week and noticed that all the chairs were either red, black or white. Also each table had four seats. It got me thinking if all the tables had been circular (i.e. a seating arrangement RRBW is the same as RBWR etc.) and every table had four chairs with a different arrangement from any other table, what would be the largest possibe cafe size.
In other words how many possible ways are there to arrange four chairs, each being either Red, Black or White, around a circular table.
I think it's fair to say that the answer is bigger than the number of tables my local cafe actually has!!
link to original post
The possible sets of chairs:
4,0,0: 3 (colors) x 1 (permutation) = 3
RRRR, WWWW, BBBB
3,1,0: 3 (colors for the 3) x 2 (colors for the 1) x 1 (permutation) = 6
RRRW, RRRB
BBBR, BBBW
WWWR, WWWB
2,2,0: 3 (pairs of colors) x 2 (permutations) = 6
RRBB, RBRB
RRWW, RWRW
BBWW, BWBW
2,1,1: 3 (colors for the pair) x 3 (permutations) = 9
RRBW, RRWB, RWRB
BBWR, BBRW, BWBR
WWRB, WWBR, WBWR
Total = 3 + 6 + 6 + 9 = 24 tables

Suppose you have a partially full bottle of pancake syrup in an unusually shaped bottle.
The bottle is 12" high.
When the cap it at the top, the syrup makes it to 7" point.
When the bottle is turned upside down, the syrup makes it to the 9" point.
What ratio of the bottle is full?
Quote: MichaelBluejayUm, 2/3? Is it as simple as taking the average of 7 and 9, and dividing by 12?
link to original post
I started to write a post why your answer was wrong, but in the process I think I find that there isn't enough information given to solve it.
I request we change the shape of the bottle to a wine bottle, where the vast majority is shaped like a cylinder.
All due apologies for the bad question.
My guess assuming the bottom 7 inches are all cylindrical....
Turn it upside down and the first 5" is what was above the previous 7" of wine.
The next 4" are what would have been the top 4" of the previous 7" of wine.
So the first 5" (when inverted) must be the same volume as the bottom 3" when right side up.
So if just a cylinder, it would be 3" + 4" (original 7") + 3" (the equivalent of the 5" inverted)
So original is 7/10 = 70%
But then again I don't like wine, so what do I know.
Quote: chevy
My guess assuming the bottom 7 inches are all cylindrical....
Turn it upside down and the first 5" is what was above the previous 7" of wine.
The next 4" are what would have been the top 4" of the previous 7" of wine.
So the first 5" (when inverted) must be the same volume as the bottom 3" when right side up.
So if just a cylinder, it would be 3" + 4" (original 7") + 3" (the equivalent of the 5" inverted)
So original is 7/10 = 70%
But then again I don't like wine, so what do I know.
link to original post
I agree!
Quote: WizardSuppose you have a partially full bottle of pancake syrup in an unusually shaped bottle.
The bottle is 12" high.
When the cap it at the top, the syrup makes it to 7" point.
When the bottle is turned upside down, the syrup makes it to the 9" point.
What ratio of the bottle is full?
link to original post
Assume the bottle is in the shape of two cylinders, one of height 7 and base area 1, and the other of height 5 and base area B.
When the base 1 cylinder is on the bottom, the liquid fills it, but there is no excess that goes into the base B cylinder
The volume = 7 x 1 = 7
When the base B cylinder is on the bottom, the liquid fills it, and there is an excess that partially fills the base 1 cylinder to a height of 4
The volume = B x 5 + 1 x 4 = 4 + 5B
Since the volume of the liquid is the same in both cases, 4 + 5B = 7, or B = 3/5
The total volume of the bottle = 7 x 1 + 5 x 3/5 = 10
The ratio that is full in this case is 7 / 10
1. Express each of the integers from 1 to 28 in the form:
A # B # C # D
where A, B, C, D are some permutation of 1, 2, 3, 4, and each # is either the addition, subtraction, or multiplication operators, but not division (they do not have to be the same operator - e.g. 1 can be 2 x 3 - 4 - 1); you may use parentheses, but there must be an operator between each pair of adjacent numbers rather than using "implied multiplication."
You also cannot use exponentiation (e.g. 23) or concatenating two digits (e.g. using 2 and 4 to make 42).
2. Express each of the integers from 1 to 15 the same way, but without parentheses, and using standard precedence.
Oh, wait; you can't - but you can do it for all but one of them.
Which one? You tell me - then express that one without parentheses if you are allowed to include the division operator.
1 | 3x2-4-1 |
2 | 3+2+1-4 |
3 | 3x2-4+1 |
4 | 4x2-3-1 |
5 | 4x1+3-2 |
6 | 4x2-3+1 |
7 | 3x(4-2)+1 |
7 | 3x4/2-1 |
8 | 4+3+2-1 |
9 | 4+3+2x1 |
10 | 4+3+2+1 |
11 | 4x3-2+1` |
12 | 4x2+3+1 |
13 | 4x3+2-1 |
14 | 4x3+2x1 |
15 | 4x3+2+1 |
16 | 4x(3+2-1) |
17 | (4+2)x3-1 |
18 | (4+2)x3x1 |
19 | (4+2)x3+1 |
20 | (3+2)x4x1 |
21 | (4+2+1)x3 |
22 | (4x3-1)x2 |
23 | 4x3x2-1 |
24 | 4x3x2x1 |
25 | 4x3x2+1 |
26 | (4x3+1)x2 |
27 | 3x(4x2+1) |
28 | 4x(3x2+1) |
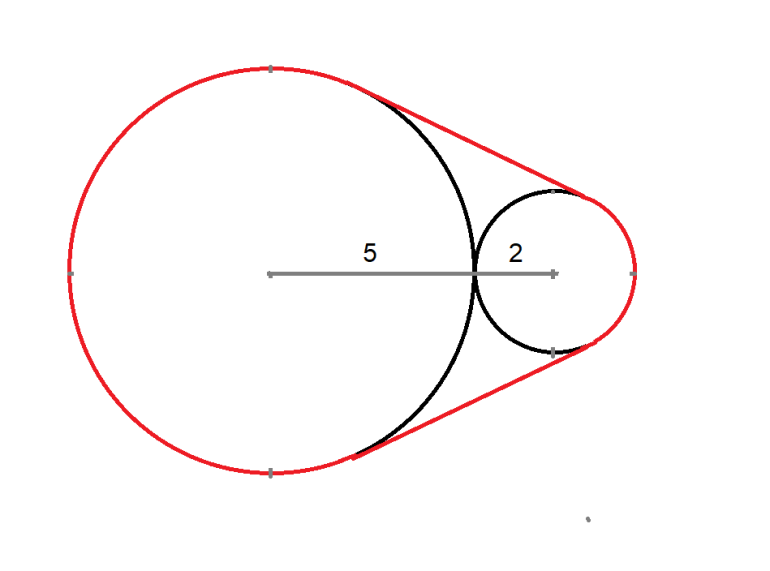
A rubber band is wrapped around two circles. The large circle has radius 5. The small circle has radius 2.
What is the distance of the rubber band?
For purposes of discussion, feel free to use...
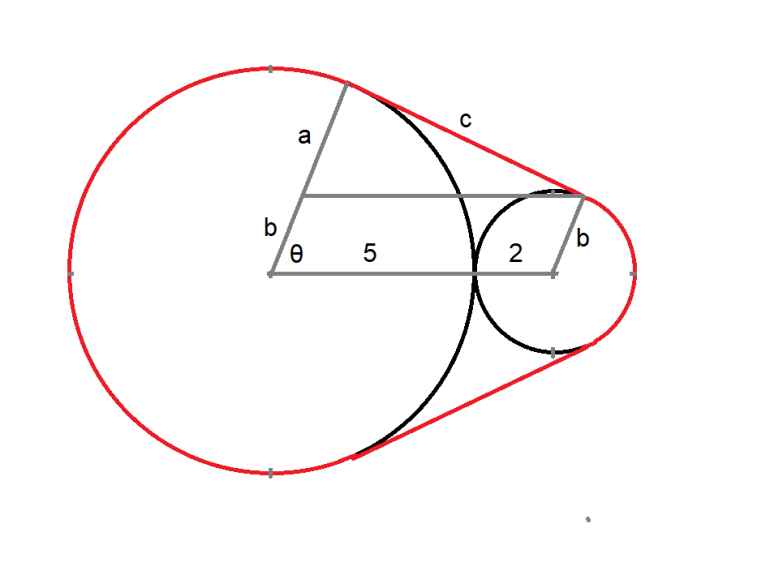
θ is an angle.
Quote: Wizard
A rubber band is wrapped around two circles. The large circle has radius 5. The small circle has radius 2.
What is the distance of the rubber band?
For purposes of discussion, feel free to use...
θ is an angle.
link to original post
mine based on your original drawing and labels.....
d = b = 2
a+b = 5+2 = 7
d+e = 2+e = 5 .... so e = 3
So c^2 = 7^2 - 3^2 = 40.....c=sqrt(40)=2sqrt(10)
There are 2 "c" legs for rubber band
Angle t = arccos(3/7) (in radians)
So angle of rubber stretched on big circle = (2pi - 2t)
So length of rubber band around big circle = (2pi-2t)*5 = 10pi - 10arccos(3/7)
small angle in Wiz's triangle is arcsin(3/7) (in radians)
So angle of rubber stretched on small circle = 2pi - 2*(pi/2 + arcsin(3/7)) = pi-2arcsin(3/7)
So length of rubber band around small circle = (pi-2arcsin(3/7))*2
total = 4sqrt(10) + (10pi-10arccos(3/7)) + (2pi - 4arcsin(3/7))
= 4 sqrt(10) + 12pi - 10arccos(3/7) - 4arcsin(3/7)
(+/- typos....and if you need something without arches or arcsin....I wave the red flag of submission)
Quote: chevy
mine based on your original drawing and labels.....
d = b = 2
a+b = 5+2 = 7
d+e = 2+e = 5 .... so e = 3
So c^2 = 7^2 - 3^2 = 40.....c=sqrt(40)=2sqrt(10)
There are 2 "c" legs for rubber band
Angle t = arccos(3/7) (in radians)
So angle of rubber stretched on big circle = (2pi - 2t)
So length of rubber band around big circle = (2pi-2t)*5 = 10pi - 10arccos(3/7)
small angle in Wiz's triangle is arcsin(3/7) (in radians)
So angle of rubber stretched on small circle = 2pi - 2*(pi/2 + arcsin(3/7)) = pi-2arcsin(3/7)
So length of rubber band around small circle = (pi-2arcsin(3/7))*2
total = 4sqrt(10) + (10pi-10arccos(3/7)) + (2pi - 4arcsin(3/7))
= 4 sqrt(10) + 12pi - 10arccos(3/7) - 4arcsin(3/7)
(+/- typos....and if you need something without arches or arcsin....I wave the red flag of submission)
link to original post
I agree! I couldn't express is more simply than that, so full credit!
Consider a game of rock-paper-scissors where:
- If rock beats scissors, scissors pays rock $1
- If scissors beats paper, paper pays scissors $2
- If paper beats rock, rock pays paper $3
- No money changes hands on a tie
Assume two logicians are playing. What is the optimal strategy for each?
Quote: WizardThis one is probably not "easy," so all due apologies for putting it here.
Consider a game of rock-paper-scissors where:
- If rock beats scissors, scissors pays rock $1
- If scissors beats paper, paper pays scissors $2
- If paper beats rock, rock pays paper $3
- No money changes hands on a tie
Assume two logicians are playing. What is the optimal strategy for each?
link to original post
Let p be the probability of playing paper, and s the probability of playing scissors; (1 - p - s) is the probability of playing rock
Expected values of the strategy, if the opponent plays:
Rock: 3p - s
Paper: 2s - 3(1 - p - s) = 5s + 3p - 3
Scissors: (1 - p - s) - 2p = 1 - s - 3p
Assuming an equilibrium (i.e. all EVs = 0):
5s + 3p - 3 = 3p - s -> s = 1/2
1 - s - 3p = 3p - s -> p = 1/6
Check:
Rock = 3p - s = 0
Paper = 5s + 3p - 3 = 0
Scissors = 1 - s - 3p = 0
Each player rolls a 6-sided die, and plays scissors on 1-3, rock on 4-5, and paper on 6
Quote: ThatDonGuy
Let p be the probability of playing paper, and s the probability of playing scissors; (1 - p - s) is the probability of playing rock
Expected values of the strategy, if the opponent plays:
Rock: 3p - s
Paper: 2s - 3(1 - p - s) = 5s + 3p - 3
Scissors: (1 - p - s) - 2p = 1 - s - 3p
Assuming an equilibrium (i.e. all EVs = 0):
5s + 3p - 3 = 3p - s -> s = 1/2
1 - s - 3p = 3p - s -> p = 1/6
Check:
Rock = 3p - s = 0
Paper = 5s + 3p - 3 = 0
Scissors = 1 - s - 3p = 0
Each player rolls a 6-sided die, and plays scissors on 1-3, rock on 4-5, and paper on 6
link to original post
I agree! Not only the correct answer, but the solution was very simply and elegantly stated.
That one is beer worthy!
The expected value based on each of the opponent's plays is:
Rock: q P - (1 - p - q) R = p R + q (P + R) - R
Paper: (1 - p - q) S - p P = S - p (P + S) - q S
Scissors: p R - q S
Assuming a Nash Equilibrium, EV(Rock) = EV(Scissors) when:
p R + q (P + R) - R = p R - q S
q = R / (R + P + S)
EV(Paper) = EV(Scissors) when:
S - p (P + S) - q S = p R - q S
p = S / (R + P + S)
1 - q - p = P / (R + P + S)
Check:
Rock: p R + q (P + R) - R = RS / (R + P + S) + R (P + R) / (R + P + S) - R = 0
Paper: S - p (P + S) - q S = S - (P + S) S / (R + P + S) - RS / (R + P + S) = 0
Scissors: RS / (R + P + S) - SR / (R + P + S) = 0
Play Rock, Paper, Scissors in the proportion S, R, P
i.e. play each in proportion to what the move that this move beats would collect if it was the winning move
Quote: acesideI recently played a 6-deck automatic-shuffle blackjack game. Everything was normal except one thing, that is, 3 of the 6 decks of cards had a red back and the remaining 3 decks of cards had a blue back. Can a player gain some EV edge from this game by taking into account the card back color information?
link to original post
If it wasn't automatic shuffle, I would say yes - for example, if you have seen all 12 blue-backed Aces come out and the next card is blue, then you know it's not an Ace - although I doubt you could get much better information than by straight card counting, especially as you would have to keep track of simultaneous red and blue counts and you can't be certain what the color of the cards after the next one will be.
However, with automatic shuffle, it may depend on how long it takes for a dealt card to make its way back into the shuffler. My gut answer is, "Not without either going to great pains to maintain counts." You could try counting just the blue cards, although the problem is the same as before - you have no idea what the backs of the cards after the next one out, if that, are going to be.
Here is what I think about this. To play this game, we need to adjust the basic strategy, especially on the hand of 16vs10. If all the exposed cards are of the same back color, we hit if the next card has the same back color, but we stand if the next card has a different back color.
Quote: acesideI recently played a 6-deck automatic-shuffle blackjack game. Everything was normal except one thing, that is, 3 of the 6 decks of cards had a red back and the remaining 3 decks of cards had a blue back. Can a player gain some EV edge from this game by taking into account the card back color information?
link to original post
A small benefit could be gained by keeping separate blue and red counts. I would only do this with a confederate, one counting each color, and communicating the information. However, I don't think the gain in EV would be enough to warrant the bother. I think more money could be made with both counters at separate tables.
By the way, I think you should have made a separate thread for this. I like to keep this thread on just fun math and logic puzzles. I'll split this discussion off it engenders more than 2 or 3 more posts.
A prisoner is presented with three closed doors, labeled A, B, and C. The warden explains that behind two doors is freedom and behind one is immediate death. The prisoner may point to one door and ask one yes/no question of the warden.
If the prisoner points towards a door leading to freedom, the warden will answer truthfully. If the prisoner points towards a door leading to death, the warden will answer yes or no randomly.
What should the prisoner do?
I thought this question sounded familiar so I used the search function here. You asked it March of last year. It is on page 262 of this thread. It is still a good question thoughQuote: WizardI apologize if I've asked this before.
A prisoner is presented with three closed doors, labeled A, B, and C. The warden explains that behind two doors is freedom and behind one is immediate death. The prisoner may point to one door and ask one yes/no question of the warden.
If the prisoner points towards a door leading to freedom, the warden will answer truthfully. If the prisoner points towards a door leading to death, the warden will answer yes or no randomly.
What should the prisoner do?
link to original post
Quote: avianrandyI thought this question sounded familiar so I used the search function here. You asked it March of last year. It is on page 262 of this thread. It is still a good question though
link to original post
Good memory!


