Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
--------------------------
Roll #11 ⚂ ⚀ ⚅ ⚀ ⚃
What is the value?
2
ThatDonGuy has risen from the ranks of the initiates and become a Potentate of the Rose. Congratulations!
The doors to the Temple of the Rose have closed.
Hail the new Potentates Dieter & ThatDonGuy!!!
----------------------------------------------------
----------------------------------------------------
Still in play...
Quote: charliepatrickSods' law!
Here is a really easy puzzle based on my experience this afternoon waiting for a bus. There are two buses (U1C and 1) that regularly go into town from where I live. For mathematical purposes they depart from their depots (University or Winchester) every 10 minutes or every 15 minutes during the daytime. However as you don't know how bad the traffic is that day you can't tell for sure when they will arrive, just that they are always 10 and 15 minutes apart. What is the chances you have to wait 9 minutes or more for the next bus into town!!
I'll be repeating this experiment later this evening to go to the pub!
link to original post
Quote: ThatDonGuyToughie Tuesday is the word for it - I don't think there's a "direct" way to solve it, as I end up with a polynomial of degree 5, which has no general solution.
link to original post
Actually, it turns out that there is a "direct" way to do it in this case.
The solution is 3 N^5 - 52 N^4 + 65 N^3 - 26 N^2 + 10 N > 0
This is N (N-1) (3 N^3 - 49 N^2 + 16 N - 10) > 0
There is a single N > 1 where this = 0, but I think it is of the form (a + sqrt(a^2 + b^2))^(1/3) + (a - sqrt(a^2 + b^2))^(1/3) + c.
Quote: charliepatrickSods' law!
Here is a really easy puzzle based on my experience this afternoon waiting for a bus. There are two buses (U1C and 1) that regularly go into town from where I live. For mathematical purposes they depart from their depots (University or Winchester) every 10 minutes or every 15 minutes during the daytime. However as you don't know how bad the traffic is that day you can't tell for sure when they will arrive, just that they are always 10 and 15 minutes apart. What is the chances you have to wait 9 minutes or more for the next bus into town!!
I'll be repeating this experiment later this evening to go to the pub!
link to original post
Let the two routes be Route 10, which runs every 10 minutes, and Route 15, which runs every 15 minutes
Assume the Route 10 bus runs at time 0, 10, 20, 30, 40, and so on
We do not know the "stagger" between the routes; assume Route 15 runs at time N, N + 15, N + 30, N + 45, and so on, with 0 <= N < 15.
If N <= 5, then the only times the wait time will be 9 minutes or more are:
(a) between time 20 and time 21
(b) if N < 1, between 0 and N
(c) if N > 4, between 10 and N + 5
If you graph the arrival time against N, the area where the wait time >= (1 x 5) + (1/2 x 1) + (1/2 x 1) = 6
Using similar reasoning, the areas for 5 < N <= 10 and 10 < N <= 15 are also each 6, so the total area is 18.
Since N is from 0 to 15 and your arrival time is from 0 to 30, the total area of the graph = 450, so the probability of a long wait is 18 / 450 = 1 / 25.
The probability that you don't arrive within 9 minutes of a 15-minute bus is 2/5.
Since the buses run independently, and you have no idea what the "stagger" of the 15-minute buses is, the probability that you don't arrive within 9 minutes of either one is 1/10 x 2/5 = 1/25.
Quote: ThatDonGuyQuote: ThatDonGuyToughie Tuesday is the word for it - I don't think there's a "direct" way to solve it, as I end up with a polynomial of degree 5, which has no general solution.
link to original post
Actually, it turns out that there is a "direct" way to do it in this case.The solution is 3 N^5 - 52 N^4 + 65 N^3 - 26 N^2 + 10 N > 0
This is N (N-1) (3 N^3 - 49 N^2 + 16 N - 10) > 0
There is a single N > 1 where this = 0, but I think it is of the form (a + sqrt(a^2 + b^2))^(1/3) + (a - sqrt(a^2 + b^2))^(1/3) + c.
link to original post
And it turns out...
N = ( (108,280 + 27 sqrt(311,783))^(1/3) + (108,280 - 27 sqrt(311,783))^(1/3)) + 49 ) / 9
Courtesy of the Wolfram Aplha Cubic Equation Solver
Quote: Ace2So what�s the expected waiting time for the next bus to arrive?
link to original post
I don't have the time to generate an image with math symbols, so you might have a little trouble reading the solution.
Let the intervals be A and B, where A < B.
The expected time = (INTEGRAL(0, A) (INTEGRAL(0, B) min(x, y) dy) dx) / (AB)
= (INTEGRAL(0, A) (INTEGRAL(0, x) y dy + INTEGRAL(x, B) x dy) dx) /.(AB)
= INTEGRAL(0, A) (x^2 / 2 + B x - x^2) dx / (AB)
= INTEGRAL(0, A) (B x - x^2) dx / (AB)
= (A^2 B / 2 - A^3 / 6) / AB
= A / 2 - A^2 / (6B)
In the problem, A = 10 and B = 15, so the expected time = 5 - 100/90 = 35/9
The first ten numbers in a sequence of positive integers are:
1, 2, 3, 130, 131, 132, 133, 120, 121, 122
What is the 100th number in the sequence?
Impressive. It clearly must be less than five minutes since that�s the average wait for the more frequent busQuote: ThatDonGuyQuote: Ace2So what�s the expected waiting time for the next bus to arrive?
link to original post
I don't have the time to generate an image with math symbols, so you might have a little trouble reading the solution.General solution:
Let the intervals be A and B, where A < B.
The expected time = (INTEGRAL(0, A) (INTEGRAL(0, B) min(x, y) dy) dx) / (AB)
= (INTEGRAL(0, A) (INTEGRAL(0, x) y dy + INTEGRAL(x, B) x dy) dx) /.(AB)
= INTEGRAL(0, A) (x^2 / 2 + B x - x^2) dx / (AB)
= INTEGRAL(0, A) (B x - x^2) dx / (AB)
= (A^2 B / 2 - A^3 / 6) / AB
= A / 2 - A^2 / (6B)
In the problem, A = 10 and B = 15, so the expected time = 5 - 100/90 = 35/9
link to original post
Quote: ThatDonGuyQuote: Ace2So what�s the expected waiting time for the next bus to arrive?
link to original post
I don't have the time to generate an image with math symbols, so you might have a little trouble reading the solution.
link to original post
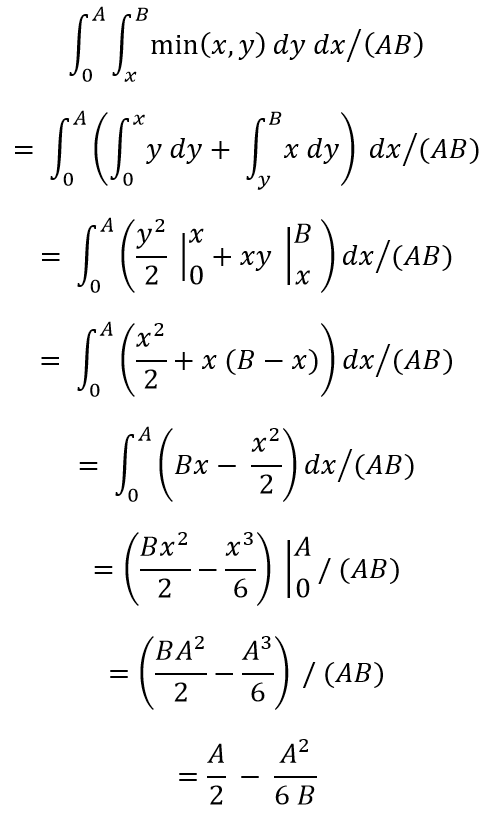
In this case, A = 10 and B = 15, so the solution is 5 - 100 / 90 = 35 / 9 minutes.
Quote: charliepatrick
Here is a really easy puzzle based on my experience this afternoon waiting for a bus. There are two buses (U1C and 1) that regularly go into town from where I live. For mathematical purposes they depart from their depots (University or Winchester) every 10 minutes or every 15 minutes during the daytime. However as you don't know how bad the traffic is that day you can't tell for sure when they will arrive, just that they are always 10 and 15 minutes apart. What is the chances you have to wait 9 minutes or more for the next bus into town!!
link to original post
Sorry for the late arrival.
Quote: ThatDonGuyAnd here's my next problem:
The first ten numbers in a sequence of positive integers are:
1, 2, 3, 130, 131, 132, 133, 120, 121, 122
What is the 100th number in the sequence?
link to original post
No takers yet?
Quote: charliepatrick
Here is a really easy puzzle based on my experience this afternoon waiting for a bus. There are two buses (U1C and 1) that regularly go into town from where I live. For mathematical purposes they depart from their depots (University or Winchester) every 10 minutes or every 15 minutes during the daytime. However as you don't know how bad the traffic is that day you can't tell for sure when they will arrive, just that they are always 10 and 15 minutes apart. What is the chances you have to wait 9 minutes or more for the next bus into town!!
link to original post
I know this one is old news, but I asked in my latest Ask the Wizard column. I changed the times to 30 and 45 minutes. Here is my solution.
Quote: ThatDonGuyQuote: ThatDonGuyAnd here's my next problem:
The first ten numbers in a sequence of positive integers are:
1, 2, 3, 130, 131, 132, 133, 120, 121, 122
What is the 100th number in the sequence?
link to original post
No takers yet?The next 10 are 123, 110, 111, 112, 113, 100, 101, 102, 103, and 230.
link to original post
I guess 330.
Quote: acesideQuote: ThatDonGuyQuote: ThatDonGuyAnd here's my next problem:
The first ten numbers in a sequence of positive integers are:
1, 2, 3, 130, 131, 132, 133, 120, 121, 122
What is the 100th number in the sequence?
link to original post
No takers yet?The next 10 are 123, 110, 111, 112, 113, 100, 101, 102, 103, and 230.
link to original post
I guess 330.
link to original post
Quote: Ace2I thought I had it until I saw 230. Must be something in base 4
link to original post
Both wrong, but at least one of you is on the right track.
Remember, I want the 100th number in the sequence.
Quote: ThatDonGuy...Both wrong, but at least one of you is on the right track.
Remember, I want the 100th number in the sequence.
Quote: charliepatrickQuote: ThatDonGuy...Both wrong, but at least one of you is on the right track.
Remember, I want the 100th number in the sequence.I did spot it had something to do with base and then had a play using a base of -4. This gives 10010=13330-4.
link to original post
That is correct!
For example, 20 = 2 x (-4)^2 + 3 x (-4) + 0 x 1, so it is 230 in base -4.
1 x (-4)^4 + 3 x (-4)^3 + 3 x (-4)^2 + 3 x (-4)^1 + 0 x 1 = 256 - 192 + 48 - 12 = 100, so 100 converted to base -4 is 13330.
I don�t see -4 as a valid counting base. The problem uses some, but not all, of the required properties of a valid base
I know how the system works and also that:Quote: charliepatrickIf you think about a base then the numbers 1, 2, 3 etc will always mean 1, 2, 3 until one reaches 10. That is because it is the Units column, so says how many units there are. When you get to 10 then that means 1 x Base + 0 x Units. This is why, in this case, you need the Hundreds to add more before the Base hits in. Interesting 13 would be what you are looking for to go the other way!
link to original post
A system that uses digits 0-9 is base 10
A system that uses digits 0-5 is base 6
A system that uses digits 0-3 is base 4
A system that uses digits 0-3 is NOT base -4
DisagreeQuote: ThatDonGuyQuote: charliepatrickQuote: ThatDonGuy...Both wrong, but at least one of you is on the right track.
Remember, I want the 100th number in the sequence.I did spot it had something to do with base and then had a play using a base of -4. This gives 10010=13330-4.
link to original post
That is correct!The numbers are 1, 2, 3, and so on in "base -4" - that is, the rightmost digit is the 1s digit, the second from the right is multiplied by -4, the third from the right is multiplied by (-4)^2 = 16, the fourth by (-4)^3 = -64, and so on.
For example, 20 = 2 x (-4)^2 + 3 x (-4) + 0 x 1, so it is 230 in base -4.
1 x (-4)^4 + 3 x (-4)^3 + 3 x (-4)^2 + 3 x (-4)^1 + 0 x 1 = 256 - 192 + 48 - 12 = 100, so 100 converted to base -4 is 13330.
link to original post
Incidentally, I just tried to get the logarithm of 100 using -4 as the base. Excel gave the answer of #NUM!, not 13330
I�m fairly certain that all valid counting bases are also valid logarithmic bases.
Quote: WizardQuote: charliepatrick
Here is a really easy puzzle based on my experience this afternoon waiting for a bus. There are two buses (U1C and 1) that regularly go into town from where I live. For mathematical purposes they depart from their depots (University or Winchester) every 10 minutes or every 15 minutes during the daytime. However as you don't know how bad the traffic is that day you can't tell for sure when they will arrive, just that they are always 10 and 15 minutes apart. What is the chances you have to wait 9 minutes or more for the next bus into town!!
link to original post
I know this one is old news, but I asked in my latest Ask the Wizard column. I changed the times to 30 and 45 minutes. Here is my solution.
link to original post
There's a way to solve this without calculus, using your graph (well, if you add a line to it)
The yellow section is a pyramid whose base is along the x = 1/2 line; its volume = 1/3 x (1/2 x (1/2 x 1/2)) x 1/2 = 1/48.
Draw a red line at y = 1/2 to separate the blue area into two sections - a triangle, and a rectangle.
The blue triangle is a pyramid that is the same as the yellow one, but rotated 90 degrees; its volume is also 1/48.
The blue rectangle is a prism with length 1/4 and base area 1/2 x (1/2 x (1/2 x 1/2)) = 1/16.
The total volume = 1/48 + 1/48 + 1/16 = 7/48.
The mean height = (7/48) / (1/2 x 3/4) = 7/36.
This one took me a while; I kept calculating the blue rectangle as if it was the time for the second bus to arrive.
Quote:
I'm trying to calculate the curve so I can sew a stuffed ball for a child, the surface of which consists of six sections as of an orange..
If (for example) the circumference of the sphere is 24 inches, then each section would be 12" long, and 4 " at its widest point. What equation would give the right width?
So, assume the sphere has circumference 24 inches and she is sewing six sections, each of length 12. What is the equation for the width of the section as a function of the number of inches, call it x, from the top of the section?
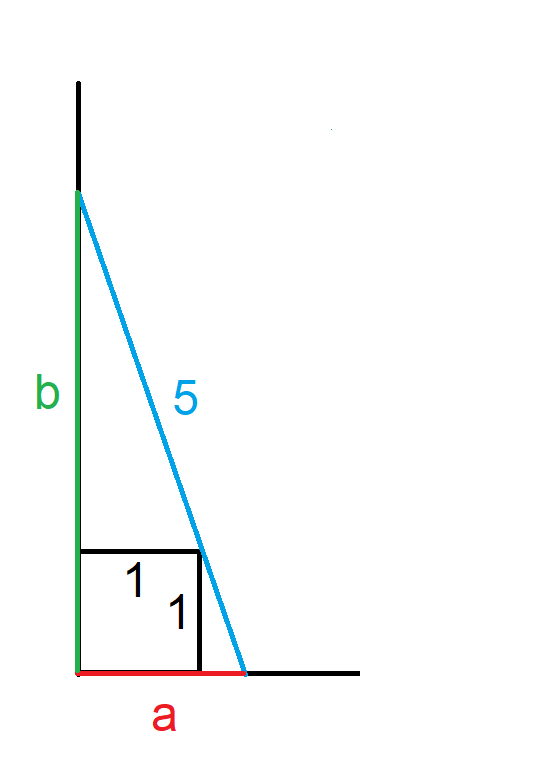
You have a 5' ladder. You wish to lean it against a wall as high as possible. However, there is a 1x1x1 cubic foot box you must put the ladder over. No, you can't move the box. What is the maximum height the top of the ladder can reach?
Quote: WizardYou have a 5' ladder. You wish to lean it against a wall as high as possible. However, there is a 1x1x1 cubic foot box you must put the ladder over. No, you can't move the box. What is the maximum height the top of the ladder can reach?
link to original post
I have a feeling there's more of a closed-form solution, but here's the closest I could come up with:
The solution is when the ladder is touching an edge of the box
The triangle with the right side of the square as one leg and the one with the top of the square as one leg are similar
(a - 1) / 1 = 1 / (b - 1)
a = 1 / (b - 1) + 1 = b / (b - 1)
Pythagorean Theorem: 5^2 = a^2 + b^2 = (b / (b - 1))^2 + b^2
25 (b - 1)^2 = b^2 + b^2 (b - 1)^2
b^4 - 2 b^3 - 23 b^2 + 50 b - 25 = 0
A little help from Excel shows that the largest solution < 5 is about 4.8385
Quote: ThatDonGuy
I have a feeling there's more of a closed-form solution, but here's the closest I could come up with:
The solution is when the ladder is touching an edge of the box
The triangle with the right side of the square as one leg and the one with the top of the square as one leg are similar
(a - 1) / 1 = 1 / (b - 1)
a = 1 / (b - 1) + 1 = b / (b - 1)
Pythagorean Theorem: 5^2 = a^2 + b^2 = (b / (b - 1))^2 + b^2
25 (b - 1)^2 = b^2 + b^2 (b - 1)^2
b^4 - 2 b^3 - 23 b^2 + 50 b - 25 = 0
A little help from Excel shows that the largest solution < 5 is about 4.8385
link to original post
I agree with the answer to four decimal places. Half a point to you. The first closed form solution gets the other half point.
Quote: WizardQuote: ThatDonGuy
I have a feeling there's more of a closed-form solution, but here's the closest I could come up with:
The solution is when the ladder is touching an edge of the box
The triangle with the right side of the square as one leg and the one with the top of the square as one leg are similar
(a - 1) / 1 = 1 / (b - 1)
a = 1 / (b - 1) + 1 = b / (b - 1)
Pythagorean Theorem: 5^2 = a^2 + b^2 = (b / (b - 1))^2 + b^2
25 (b - 1)^2 = b^2 + b^2 (b - 1)^2
b^4 - 2 b^3 - 23 b^2 + 50 b - 25 = 0
A little help from Excel shows that the largest solution < 5 is about 4.8385
link to original post
I agree with the answer to four decimal places. Half a point to you. The first closed form solution gets the other half point.
link to original post
b = (1 / 2) * {1 + sqrt(26) + sqrt[23 - 2*sqrt(26)]}
I simplified the equation to a quartic equation that I couldn't solve without numerical methods, so I had wolframalpha give me the solution in closed form.


Quote: Wizard
You have a 5' ladder. You wish to lean it against a wall as high as possible. However, there is a 1x1x1 cubic foot box you must put the ladder over. No, you can't move the box. What is the maximum height the top of the ladder can reach?
link to original post
You never said the ladder had to touch the floor! ;-)
Seriously:
POLYMATH Results
05-03-2023, Rev5.1.225
NLES Solution
Variable Value f(x) Ini Guess
a 1.2605183 -1.066E-14 0.1
b 4.8385012 1.776E-15 2
c 3.9666222 -7.883E-15 3
NLES Report (constrained)
Nonlinear equations
[1] f(a) = 5^2-a^2-b^2 = 0
[2] f(b) = c^2-(b-1)^2-1^2 = 0
[3] f(c) = (5-c)^2-(a-1)^2-1^2 = 0
Conditions for solution
[1] a : Absolutely Positive
[2] b : Absolutely Positive
[3] c : Absolutely Positive
Settings
Convergence tolerance = 0.0000001
Maxumum # of iterations = 150
# of iterations used = 25
General
number of implicit equations: 3
number of explicit equations: 0
So the height is b = 4.8385012 ft
Dog Hand
Nice! Wolfram Alpha solves it in closed form, if you are interested.Quote: ThatDonGuyQuote: WizardYou have a 5' ladder. You wish to lean it against a wall as high as possible. However, there is a 1x1x1 cubic foot box you must put the ladder over. No, you can't move the box. What is the maximum height the top of the ladder can reach?
link to original post
I have a feeling there's more of a closed-form solution, but here's the closest I could come up with:
The solution is when the ladder is touching an edge of the box
The triangle with the right side of the square as one leg and the one with the top of the square as one leg are similar
(a - 1) / 1 = 1 / (b - 1)
a = 1 / (b - 1) + 1 = b / (b - 1)
Pythagorean Theorem: 5^2 = a^2 + b^2 = (b / (b - 1))^2 + b^2
25 (b - 1)^2 = b^2 + b^2 (b - 1)^2
b^4 - 2 b^3 - 23 b^2 + 50 b - 25 = 0
A little help from Excel shows that the largest solution < 5 is about 4.8385
link to original post
a2 - bc = 5
b2 - ac = 7
c2 - ab = 9
Solve for a, b, and c.
p.s. This was puzzle was inspired by a similar one on YouTube. I'll post a link to it later. If you've already seen the video, please recuse yourself from the discussion, for now, and let everyone else enjoy it.
Rule: Each of four cards has a letter on one side and a number on the opposite side
You are shown these four cards:
Card A = E
Card B = G
Card C = 2
Card D = 3
You are told of an hypothesis that every card with a vowel on one side has an even number on the opposite side. Which card or cards must you turn over to check whether the hypothesis is true?
Please put answers in spoiler boxes.
x = -19/(3 sqrt(7)) ∧; y = 2/(3 sqrt(7)) ; z = 23/(3 sqrt(7))
x = 19/(3 sqrt(7)) ∧; y = -2/(3 sqrt(7)) ; z = -23/(3 sqrt(7))
Quote: gordonm888Here's an easier puzzle to chew on.
Rule: Each of four cards has a letter on one side and a number on the opposite side
You are shown these four cards:
Card A = E
Card B = G
Card C = 2
Card D = 3
You are told of an hypothesis that every card with a vowel on one side has an even number on the opposite side. Which card or cards must you turn over to check whether the hypothesis is true?
Please put answers in spoiler boxes.
link to original post
My, quite possibly incorrect, answer is A and D only.
If A is odd, we have disproven the hypothesis and are done.
If D has a vowel, we have disproven the hypothesis and are done.
B doesn't have a vowel, so wouldn't lend evidence either way, whatever was on the other side.
If A and D have conformed to the theory, turning over C could either conform to the theory or be a consonant and not help either way.
Quote: acesideUsing an online equation solver, I got
x = -19/(3 sqrt(7)) ∧; y = 2/(3 sqrt(7)) ; z = 23/(3 sqrt(7))
x = 19/(3 sqrt(7)) ∧; y = -2/(3 sqrt(7)) ; z = -23/(3 sqrt(7))
link to original post
I agree with the answer, however zero credit for using an equation solver.
Quote: WizardIt's Toughie Tuesday! This simple problem is surprisingly tricky to solve.
a2 - bc = 5
b2 - ac = 7
c2 - ab = 9
Solve for a, b, and c.
link to original post
Subtract the first equation from the second:
(b^2 - a^2) + (b - a) c = 2
(b - a) (a + b + c) = 2
Subtract the second equation from the third:
(c^2 - b^2) + (c - b) a = 2
(c - b) (a + b + c) = 2
Since the products are nonzero, none of the terms are zero, so b - a = c - b = 2 / (a + b + c)
Substitute b - x for a, and b + x for c:
In the second equation:
b^2 - (b + x)(b - x) = 7
x = sqrt(7)
Now, substitute for a and c in the first equation:
(b - sqrt(7))^2 - b (b + sqrt(7)) = 5
b^2 - 2 sqrt(7) b + 7 - b^2 - sqrt(7) b = 5
- 3 sqrt(7) b = -2
b = 2 / (3 sqrt(7)) = 2 sqrt(7) / 21
a = b - x = (2 sqrt(7) - 21 sqrt(7)) / 21 = -19 sqrt(7) / 21
c = b + x = (2 sqrt(7) + 21 sqrt(7)) / 21 = 23 sqrt(7) / 21
Quote: WizardQuote: acesideUsing an online equation solver, I got
x = -19/(3 sqrt(7)) ∧; y = 2/(3 sqrt(7)) ; z = 23/(3 sqrt(7))
x = 19/(3 sqrt(7)) ∧; y = -2/(3 sqrt(7)) ; z = -23/(3 sqrt(7))
link to original post
I agree with the answer, however zero credit for using an equation solver.
link to original post
Eq1-Eq2 = (a-b)(a+b+c) =-2;
Eq2-Eq3 = (b-c)(a+b+c) =-2;
Therefore, we have
a-b =b-c.
Solving this, we have b =(a+c)/2 and plug it into Eq2,
[(a+c)/2]^2 - a*c =7.
Simplifing this, we have a =c + 2 Sqrt(7); or a =c - 2 Sqrt(7);
We plug a =c + 2 Sqrt(7) into Eq3 to get
c =-23/[3 sqrt(7)];
Then we will get a and b easily.
Quote: WizardQuote: gordonm888Here's an easier puzzle to chew on.
Rule: Each of four cards has a letter on one side and a number on the opposite side
You are shown these four cards:
Card A = E
Card B = G
Card C = 2
Card D = 3
You are told of an hypothesis that every card with a vowel on one side has an even number on the opposite side. Which card or cards must you turn over to check whether the hypothesis is true?
Please put answers in spoiler boxes.
link to original post
My, quite possibly incorrect, answer is A and D only.
If A is odd, we have disproven the hypothesis and are done.
If D has a vowel, we have disproven the hypothesis and are done.
B doesn't have a vowel, so wouldn't lend evidence either way, whatever was on the other side.
If A and D have conformed to the theory, turning over C could either conform to the theory or be a consonant and not help either way.
link to original post
Wizard and Aceside both gave correct answers.
In tests conducted by psychologists, only 4% of subjects gave the correct answer.
The key to the question is to carefully read the problem statement and to apply the criterion precisely, which is a skill that almost everyone on this thread seems to have developed.
This problem is discussed in the book: 'Symmetry' by Marcus du Sautoy, p.278
Quote: WizardWhat is the expected number of spins in double-zero roulette to see five reds or five blacks in a row? The previous spin landed on 0.
link to original post
Quote: EdCollinsQuote: WizardWhat is the expected number of spins in double-zero roulette to see five reds or five blacks in a row? The previous spin landed on 0.
link to original postI'll go ahead and take a stab at it and say the expected number of spins is 14.93.
link to original post
That's not what I get, but maybe I'm wrong.
Quote: WizardQuote: EdCollinsQuote: WizardWhat is the expected number of spins in double-zero roulette to see five reds or five blacks in a row? The previous spin landed on 0.
link to original postI'll go ahead and take a stab at it and say the expected number of spins is 14.93.
link to original post
That's not what I get, but maybe I'm wrong.
link to original post
Quote: WizardWhat is the expected number of spins in double-zero roulette to see five reds or five blacks in a row? The previous spin landed on 0.
link to original post
Let E(n) be the expected number after having n consecutive of a color; E(5) = 0
Let p be the probability of getting a particular color, and r = 1 - 2p = the probability that it comes up green
E(4) = 1 + p E(1) + r E(0)
E(3) = 1 + p E(1) + r E(0) + p E(4)
= 1 + p E(1) + r E(0) + p (1 + p E(1) + r E(0))
= 1 + p + (p + p^2) E(1) + (r + pr) E(0)
E(2) = 1 + p E(1) + r E(0) + p E(3)
= 1 + p E(1) + r E(0) + p (1 + p + (p + p^2) E(1) + (r + pr) E(0))
= (1 + p + p^2) + p (1 + p + p^2) E(1) + r (1 + p + p^2) E(0)
E(1) = 1 + p E(1) + r E(0) + p E(3)
= (1 + p + p^2 + p^3) + p (1 + p + p^2 + p^3) E(1) + r (1 + p + p^2 + p^3) E(0)
(1 - p - p^2 - p^3 - p^4) E(1) = (1 + p + p^2 + p^3) + (1 - 2p) (1 + p + p^2 + p^3) E(0)
E(1) = (1 + p + p^2 + p^3) / (1 - p - p^2 - p^3 - p^4) + ((1 - 2p) (1 + p + p^2 + p^3) / (1 - p - p^2 - p^3 - p^4)) E(0)
E(0) = 1 + (1 - 2p) E(0) + 2p E(1)
E(0) = 1 / 2p + E(1)
E(0) = 1 / 2p + (1 + p + p^2 + p^3) / (1 - p - p^2 - p^3 - p^4) + ((1 - 2p) (1 + p + p^2 + p^3) / (1 - p - p^2 - p^3 - p^4)) E(0)
(1 - (1 - 2p) (1 + p + p^2 + p^3) / (1 - p - p^2 - p^3 - p^4)) E(0) = 1 / 2p + (1 + p + p^2 + p^3) / (1 - p - p^2 - p^3 - p^4)
E(0) = (1 / 2p + (1 + p + p^2 + p^3) / (1 - p - p^2 - p^3 - p^4)) x (1 - p - p^2 - p^3 - p^4) / p^4
E(0) = (1 - p - p^2 - p^3 - p^4) / (2 p^5) + (1 + p + p^2 + p^3) / p^4
E(0) = (1 - p - p^2 - p^3 - p^4) / (2 p^5) + (2p + 2p^2 + 2p^3 + 2p^4) / (2p^5)
= (1 + p + p^2 + p^3 + p^4) / (2p^5)
= (1 - p^5) / (2 p^5 (1 - p))
For p = 9/19, this is 4,592,395 / 118,098, or about 38.8863


