Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
Quote: ThatDonGuy
Since it is limited to winning bets, ignore all rolls of 7.
Also, since it is for 17 rolls or less, assume there are 17 rolls, including any rolls that would come after a winning set.
Find all increasing 7-tuples of numbers in {2, 3, 4, 5, 6, 8, 9, 10, 11, 12}. ("Increasing" means no number is greater than the one to its right.)
Let P(2) be the number of times 2 appears in the 17 rolls, P(3) the number of times 3 appears, and so on.
For example, if the 7-tuple is (2, 3, 4, 5, 6, 8, 9), then P(2) = P(3) = ... = P(9) = 2, and P(10) = P(11) = P(12) = 1; if it is (2, 2, 2, 2, 2, 2, 2),, then P(2) = 8 and P(3) = ... = P(12) = 1.
There are 17! / (P(2)! P(3)! ... P(12)!) permutations of these 17 numbers.
For each permutation, the probability of actually rolling those numbers is (1/30)^P(2) * (2/30)^P(3) * ... * (2/30)^P(11) * (1/30)^P(12).
Calculate this value for each permutation, and add them up to get:
235,436,099,899 / 8,649,755,859,375, or about 1 / 36.7393.
The solution is the integral over x from 0 to positive infinity of:
1-((1 - e^(-x/30))(1 - e^(-x/15))(1 - e^(-x/10))(1 - e^(-2/15*x))(1 - e^(-x/6))(1 - e^(-x/5)))^2 dx
which is 5,401,372,918,634,611 / 105,826,178,618,160, or about 51.04
link to original post
I haven't completed my calculation for #1, but a simulation gives a probability roughly 10x your answer.
I have calculated the expected value and supported it with my simulation. My answer is less than half of yours. Your integral gives the expected number of rolls to hit all dice sums at least once (ignoring sevens). Though we are looking at winning strings only, you still can't ignore sevens
Quote: Ace2Quote: ThatDonGuy
Since it is limited to winning bets, ignore all rolls of 7.
Also, since it is for 17 rolls or less, assume there are 17 rolls, including any rolls that would come after a winning set.
Find all increasing 7-tuples of numbers in {2, 3, 4, 5, 6, 8, 9, 10, 11, 12}. ("Increasing" means no number is greater than the one to its right.)
Let P(2) be the number of times 2 appears in the 17 rolls, P(3) the number of times 3 appears, and so on.
For example, if the 7-tuple is (2, 3, 4, 5, 6, 8, 9), then P(2) = P(3) = ... = P(9) = 2, and P(10) = P(11) = P(12) = 1; if it is (2, 2, 2, 2, 2, 2, 2),, then P(2) = 8 and P(3) = ... = P(12) = 1.
There are 17! / (P(2)! P(3)! ... P(12)!) permutations of these 17 numbers.
For each permutation, the probability of actually rolling those numbers is (1/30)^P(2) * (2/30)^P(3) * ... * (2/30)^P(11) * (1/30)^P(12).
Calculate this value for each permutation, and add them up to get:
235,436,099,899 / 8,649,755,859,375, or about 1 / 36.7393.
The solution is the integral over x from 0 to positive infinity of:
1-((1 - e^(-x/30))(1 - e^(-x/15))(1 - e^(-x/10))(1 - e^(-2/15*x))(1 - e^(-x/6))(1 - e^(-x/5)))^2 dx
which is 5,401,372,918,634,611 / 105,826,178,618,160, or about 51.04
link to original postI disagree with both.
I haven't completed my calculation for #1, but a simulation gives a probability roughly 10x your answer.
I have calculated the expected value and supported it with my simulation. My answer is less than half of yours. Your integral gives the expected number of rolls to hit all dice sums at least once (ignoring sevens). Though we are looking at winning strings only, you still can't ignore sevens
link to original post
Well, in that case, isn't the integral:
1 - ( (1 - e^(-x/36)) (1 - e^(-x/18)) (1 - e^(-x/12)) (1 - e^(-x/9)) (1 - e^(-x*5/36)) )^2 * e^(-x/6) dx ?
The online integral calculator says this diverges.
If you leave out the e^(-x/6) term...
then the solution is about 61.1858, but I know that's wrong; I think it "should be" somewhere around 21
Regarding the integral, you're not on the right path. The general method you're using won't work for scenarios with a win/loss condition.
Quote: Ace2A forum member recently posted the following (regarding the ALL craps side bet):
"You only need ten rolls to hit the ALL. Its [sic] been hit in 15-17 rolls typically."
The easy math puzzles are:
1) Assuming you win the ALL bet, what's the probability you win with less than 18 rolls?
2) Considering winning bets only, how many rolls does it take, on average, to win the ALL bet
link to original post
I will elaborate on my answer if I'm correct.
Q: You roll a pair of dice until you either get a total of 7 or 12. What is the expected number of rolls, given that a total of 12 was rolled first?
Let's look at winning where the final winning total is a 2, for example.
The probability of this is the integral from 0 to infinity of (1-exp(-x/36))*(1-exp(-2x/36))^2*(1-exp(-3x/36))^2(1-exp(-4x/36))^2*(1-exp(-5x/36))^2*exp(-x/6)*exp(-x/36)*(1/36).
This is the product of the probability all the other points have been rolled at least once, the 2 not rolled, the 7 not rolled, and the 2 rolled at any given moment. Taking this over all possible times from 0 to infinity gives the total probability.
This integral is 0.000949595.
To get the expected number of rolls that contribute to a winning bet, we throw an x into that integral.
That integral is 0.021366145.
Diving the rolls by the probability, we get 22.50027797. This is the expected rolls when a 2 is the last winning number.
We then do that for all the other possible winning totals.
The following table shows the math for totals of 2 to 6.
| Missing Point | Probability | Expected rolls | Rolls given win | Weighted expected rolls |
|---|---|---|---|---|
| 2 | 0.000949595 | 0.021366145 | 22.50027797 | 0.021366145 |
| 3 | 0.000665799 | 0.014187777 | 21.30941251 | 0.014187777 |
| 4 | 0.000463902 | 0.00935286 | 20.16126703 | 0.00935286 |
| 5 | 0.000323291 | 0.006172798 | 19.09362878 | 0.006172798 |
| 6 | 0.000226265 | 0.004099307 | 18.11725583 | 0.004099307 |
| Total | 0.002628852 | 0.055178887 |
To count for totals of 8 to 12, we double the figure in the lower right cell to get 0.110357775. This is the expected rolls that were part of a winning bet.
It has already been established the probability of winning the All bet is 0.005257704.
Dividing 0.110357775 by 0.005257704, we get the answer of 20.98972725.
That is correct! Worth two beersQuote: WizardA simulation seems to confirm my answer to Ace's part 2. Thus here are some comments on my solution in an effort to show my work.
Let's look at winning where the final winning total is a 2, for example.
The probability of this is the integral from 0 to infinity of (1-exp(-x/36))*(1-exp(-2x/36))^2*(1-exp(-3x/36))^2(1-exp(-4x/36))^2*(1-exp(-5x/36))^2*exp(-x/6)*exp(-x/36)*(1/36).
This is the product of the probability all the other points have been rolled at least once, the 2 not rolled, the 7 not rolled, and the 2 rolled at any given moment. Taking this over all possible times from 0 to infinity gives the total probability.
This integral is 0.000949595.
To get the expected number of rolls that contribute to a winning bet, we throw an x into that integral.
That integral is 0.021366145.
Diving the rolls by the probability, we get 22.50027797. This is the expected rolls when a 2 is the last winning number.
We then do that for all the other possible winning totals.
The following table shows the math for totals of 2 to 6.
Missing Point Probability Expected rolls Rolls given win Weighted expected rolls 2 0.000949595 0.021366145 22.50027797 0.021366145 3 0.000665799 0.014187777 21.30941251 0.014187777 4 0.000463902 0.00935286 20.16126703 0.00935286 5 0.000323291 0.006172798 19.09362878 0.006172798 6 0.000226265 0.004099307 18.11725583 0.004099307 Total 0.002628852 0.055178887
To count for totals of 8 to 12, we double the figure in the lower right cell to get 0.110357775. This is the expected rolls that were part of a winning bet.
It has already been established the probability of winning the All bet is 0.005257704.
Dividing 0.110357775 by 0.005257704, we get the answer of 20.98972725.
link to original post
Though I just used one long integral to get to 0.110357775. Same result
Does anyone have a solution to part 1 of the problem?
Quote: Ace2...Though I just used one long integral to get to 0.110357775.
link to original post
May I see the integral?
(((1-e^(-1x/36))^.5*(1-e^(-2x/36))*(1-e^(-3x/36))*(1-e^(-4x/36))*(1-e^(-5x/36)))^2*e^(-1x/36)*e^(-6x/36)*1/36+((1-e^(-1x/36))*(1-e^(-2x/36))^.5*(1-e^(-3x/36))*(1-e^(-4x/36))*(1-e^(-5x/36)))^2*e^(-2x/36)*e^(-6x/36)*2/36+((1-e^(-1x/36))*(1-e^(-2x/36))*(1-e^(-3x/36))^.5*(1-e^(-4x/36))*(1-e^(-5x/36)))^2*e^(-3x/36)*e^(-6x/36)*3/36+((1-e^(-1x/36))*(1-e^(-2x/36))*(1-e^(-3x/36))*(1-e^(-4x/36))^.5*(1-e^(-5x/36)))^2*e^(-4x/36)*e^(-6x/36)*4/36+((1-e^(-1x/36))*(1-e^(-2x/36))*(1-e^(-3x/36))*(1-e^(-4x/36))*(1-e^(-5x/36))^.5)^2*e^(-5x/36)*e^(-6x/36)*5/36)*2*x
I did some reformatting of the text of the equation to see if that would make it more accessible.
2*(((1-e(-x/36))½*(1-e(-2x/36))*(1-e(-3x/36))*(1-e(-4x/36))*(1-e(-5x/36)))2*e(-x/36)*e(-6x/36)*1/36
+((1-e(-x/36))*(1-e(-2x/36))½*(1-e(-3x/36))*(1-e(-4x/36))*(1-e(-5x/36)))2*e(-2x/36)*e(-6x/36)*2/36
+((1-e(-x/36))*(1-e(-2x/36))*(1-e(-3x/36))½*(1-e(-4x/36))*(1-e(-5x/36)))2*e(-3x/36)*e(-6x/36)*3/36
+((1-e(-x/36))*(1-e(-2x/36))*(1-e(-3x/36))*(1-e(-4x/36))½*(1-e(-5x/36)))2*e(-4x/36)*e(-6x/36)*4/36
+((1-e(-x/36))*(1-e(-2x/36))*(1-e(-3x/36))*(1-e(-4x/36))*(1-e(-5x/36))½)2*e(-5x/36)*e(-6x/36)*5/36)
Actually, that is indeed a bit more understandable but Hoooboy!
I donít see the x in the above integral
Quote: Ace2Does anyone have a solution to part 1 of the problem?
I have a feeling the way to solve it is to solve for 10 rolls (which I did), then use that somehow to solve for "11 or fewer", then "12 or fewer," and so on.
And I think I figured out my problem with my earlier "solution": it doesn't take into account the possibility of rolling, for example, 2 through 12 in any order, then any number of 7s.
There's actually a MUCH more efficient way to solve this:Quote: Ace2Here it is. I realize it can be simplified/reduced
(((1-e^(-1x/36))^.5*(1-e^(-2x/36))*(1-e^(-3x/36))*(1-e^(-4x/36))*(1-e^(-5x/36)))^2*e^(-1x/36)*e^(-6x/36)*1/36+((1-e^(-1x/36))*(1-e^(-2x/36))^.5*(1-e^(-3x/36))*(1-e^(-4x/36))*(1-e^(-5x/36)))^2*e^(-2x/36)*e^(-6x/36)*2/36+((1-e^(-1x/36))*(1-e^(-2x/36))*(1-e^(-3x/36))^.5*(1-e^(-4x/36))*(1-e^(-5x/36)))^2*e^(-3x/36)*e^(-6x/36)*3/36+((1-e^(-1x/36))*(1-e^(-2x/36))*(1-e^(-3x/36))*(1-e^(-4x/36))^.5*(1-e^(-5x/36)))^2*e^(-4x/36)*e^(-6x/36)*4/36+((1-e^(-1x/36))*(1-e^(-2x/36))*(1-e^(-3x/36))*(1-e^(-4x/36))*(1-e^(-5x/36))^.5)^2*e^(-5x/36)*e^(-6x/36)*5/36)*2*x
link to original post
For ALL bet calculation purposes, we can say that a shooter's turn (t) lasts an average of 6 rolls (the average time to roll a 7).
We already know that the probability (p) of winning the ALL bet is 0.0052577
Where r is the expected rolls to resolve the ALL bet, we can say that r + pt = t.
Solving for r, the expected number of rolls to resolve the bet is 5.9685
Then, taking the integral from zero to infinity of:
(1-((1-e^(-x/36))*(1-e^(-x/18))*(1-e^(-x/12))*(1-e^(-x/9))*(1-e^(-5x/36)))^2)*e^(-x/6)*1/6*x dx
Gives us an average of 5.8581 for losing bets
Which means winning bets average 5.9685 - 5.8581 = 0.1104.
That average has been multiplied by the probability of winning, so we divide it by 0.0052577 to get the answer of 20.9897 rolls as the average length of a winning ALL bet
The above figures have been rounded but the answer can be expressed exactly as a fraction if necessary
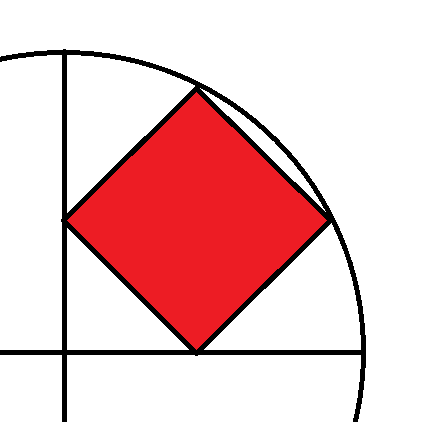
A square is inscribed in a quarter-circle of radius one. What is the area of the square?
Let x be the side length of the square.
Let O be the center of the circle, A the topmost point of the square, and B the leftmost point of the square.
Draw a line through A perpendicular to line OB; let C be where they intersect.
OB = BC = CA = (sqrt(2) / 2) x.
OCB is a right triangle.
Let t be angle COA; tan t = AC / OC = 1/2, so sin t = AC / OA = sqrt(5) / 5.
AC = (sqrt(2) / 2) x and OA = 1, so sqrt(2) / 2 x = sqrt(5) / 5, which means x = sqrt(10) / 5
The area of the square is x^2, which is 2/5.
Quote: ThatDonGuy
Let x be the side length of the square.
Let O be the center of the circle, A the topmost point of the square, and B the leftmost point of the square.
Draw a line through A perpendicular to line OB; let C be where they intersect.
OB = BC = CA = (sqrt(2) / 2) x.
OCB is a right triangle.
Let t be angle COA; tan t = AC / OC = 1/2, so sin t = AC / OA = sqrt(5) / 5.
AC = (sqrt(2) / 2) x and OA = 1, so sqrt(2) / 2 x = sqrt(5) / 5, which means x = sqrt(10) / 5
The area of the square is x^2, which is 2/5.
link to original post
I agree!
If you point to a door that leads to freedom, he will answer your question truthfully.
If you point to a door that leads to death, he will answer your question with yes or no randomly.
What question should you ask that will ensure freedom?
Quote: Ace2Does anyone have a solution to part 1 of the problem?
link to original post
Using a Markov chain, I get 3,418,341,036,467,875 / 1,999,004,627,104,432,128, or about 1 / 584.788
Quote: WizardYou are held captive by an evil warden. He takes you to a room with three doors. He explains that two doors lead to freedom and one leads to immediate death. He says you may point to any door you wish and ask a single yes/no question.
If you point to a door that leads to freedom, he will answer your question truthfully.
If you point to a door that leads to death, he will answer your question with yes or no randomly.
What question should you ask that will ensure freedom?
link to original post
"Is this the door to death, and is your answer the truth?"
If it is the freedom door, the answer is "No", and he must answer truthfully, so the answer is always "No."
If it is the death door, then the question becomes, "Is your answer the truth?"; if it is, then the answer is "Yes," and he truthfully answers "Yes"; if it is not, then the answer is "No," but he lies and answers "Yes."
If the answer is No, choose that door; if it is Yes, choose either of the other two.
I was confused for a while by the fact that there were two freedom doors.
Quote: ThatDonGuy
Let x be the side length of the square.
Let O be the center of the circle, A the topmost point of the square, and B the leftmost point of the square.
Draw a line through A perpendicular to line OB; let C be where they intersect.
OB = BC = CA = (sqrt(2) / 2) x.
OCB is a right triangle.
Let t be angle COA; tan t = AC / OC = 1/2, so sin t = AC / OA = sqrt(5) / 5.
AC = (sqrt(2) / 2) x and OA = 1, so sqrt(2) / 2 x = sqrt(5) / 5, which means x = sqrt(10) / 5
The area of the square is x^2, which is 2/5.
link to original post
Earlier I posted this in hopes that you could verify my estimate of the player's edge portion from additional blackjacks. Can you help take a look?
https://wizardofvegas.com/forum/questions-and-answers/math/36973-blackjack-card-count-probability/
Quote: acesideEarlier I posted this in hopes that you could verify my estimate of the player's edge portion from additional blackjacks. Can you help take a look?
https://wizardofvegas.com/forum/questions-and-answers/math/36973-blackjack-card-count-probability/
No, as you need something with a simulator that handles various conditions, and I don't have one of those. Solving the probability of getting a blackjack is much easier as it is just based on "the next two cards" and doesn't have to take things like splitting and doubling into account (either you have a blackjack, or you don't).
I think this problem has been pending long enough that we can stop using spoiler tagsQuote: ThatDonGuyQuote: Ace2Does anyone have a solution to part 1 of the problem?
link to original post
Using a Markov chain, I get 3,418,341,036,467,875 / 1,999,004,627,104,432,128, or about 1 / 584.788
link to original post
My simulation gives a probability nearly 200 times your answer. Perhaps you need to divide your answer by the overall probability of winning the bet?
We've established that the average length of winning bets is about 21 rolls, so I would expect a lot more than 1 in 585 to last 17 or less. If we assume a standard deviation of 21^.5 with 17.5 being 0.764 SDs to the left of expectations, that would mean about 22% of winning bets would take less than 18 rolls. This is not bad for a very rough estimate
Incidentally, I'm almost sure this problem can be solved via inclusion-exclusion. I used I-E to calculate the probability of the bet being in an unresolved state (no 7s and all numbers have not been rolled) after 17 rolls. What really complicates the calculation is that the bet can be won with 7s rolled within 17 total rolls as long as all other numbers have been rolled first. So I'll probably have to cycle though the same I-E calculation for rolls 10-16 as well to get the final answer. But, before I do that, I'm searching for a clever way to get there without more I-E calcs
Quote: Ace2My simulation gives a probability nearly 200 times your answer. Perhaps you need to divide your answer by the overall probability of winning the bet?
Why, yes - yes, I do. I forgot that the problem included the assumption that the bet was won. My answer was the probability of not only winning the bet, but doing it in 17 rolls or fewer.
Quote: ThatDonGuy
"Is this the door to death, and is your answer the truth?"
If it is the freedom door, the answer is "No", and he must answer truthfully, so the answer is always "No."
If it is the death door, then the question becomes, "Is your answer the truth?"; if it is, then the answer is "Yes," and he truthfully answers "Yes"; if it is not, then the answer is "No," but he lies and answers "Yes."
If the answer is No, choose that door; if it is Yes, choose either of the other two.
I was confused for a while by the fact that there were two freedom doors.
link to original post
I think there may be a misunderstanding on the rules.
If you point to the door that leads to death, the warden won't even listen to the question, he will say "yes" or "no" randomly.
If you point to a freedom door, then your two-part question will produce a no and a yes. Since they are not both yeses, he will say "no."
If you point to a death door, you could get either a yes or no.
So, if you get a "yes," pick either other door and you'll be liberated. However, if you get a "no" you won't know why you got a "no." If you pick that door, then it may lead to death, if the warden said "no" randomly.
If there is any further discussion of this problem, let's say the three doors are labeled A, B, and C. This will make discussion easier.
On the Price is Right they play a game six times every show with the following rules:
1. A prize is shown without revealing the price.
2. One at a time, in a specified order, the contestants bid on the price.
3. The contestant who bids the closest without going over wins.
4. If all four contestants overbid, they start over.
For the purposes of this problem, let's say the value of the prize is uniformly distributed between $0 and $1,000. Let's say contestants may bid to the penny. Furthermore, all contestants are perfect logicians and know the same information on the prize value.
What should be the bid of each contestant?
Feel free to answer for the two- and three-player cases too.
Direct: https://www.youtube.com/watch?v=15joxxXc_Bg
Quote: WizardQuote: ThatDonGuy
"Is this the door to death, and is your answer the truth?"
If it is the freedom door, the answer is "No", and he must answer truthfully, so the answer is always "No."
If it is the death door, then the question becomes, "Is your answer the truth?"; if it is, then the answer is "Yes," and he truthfully answers "Yes"; if it is not, then the answer is "No," but he lies and answers "Yes."
If the answer is No, choose that door; if it is Yes, choose either of the other two.
I was confused for a while by the fact that there were two freedom doors.
link to original post
I think there may be a misunderstanding on the rules.
If you point to the door that leads to death, the warden won't even listen to the question, he will say "yes" or "no" randomly.
If you point to a freedom door, then your two-part question will produce a no and a yes. Since they are not both yeses, he will say "no."
If you point to a death door, you could get either a yes or no.
So, if you get a "yes," pick either other door and you'll be liberated. However, if you get a "no" you won't know why you got a "no." If you pick that door, then it may lead to death, if the warden said "no" randomly.
If there is any further discussion of this problem, let's say the three doors are labeled A, B, and C. This will make discussion easier.
link to original post
The "two-part answer" is a legitimate yes or no question. "And" means that both parts have to be true in order to get a "Yes." On the other hand, had it said "Or," then only one part would need to be correct.
For example:
The answer to, "Is 2 an even number, and is 3 an even number?" is "No," since 3 is not an even number, so all of the conditions are not true.
The answer to, "Is 2 an even number, or is 3 an even number?" is "Yes," since 2 is an even number, so at least one of the conditions is true.
However, the "clarified" rules do change the question concerning when the warden can say "yes" or "no" if I point to the "door of death." In this case, since the warden can always give the same answer to any question regardless of which door I point to, I am having a hard time trying to come up with a question that can possibly work.
Reasoning: If he says yes then he's either telling the truth (meaning doors A and C are freedom) or he's lying (meaning B and C are freedom). C is freedom in both cases
If he says no then he's either telling the truth (meaning doors A and B are freedom) or he's lying (meaning B and C are freedom). B is freedom in both cases
Quote: Ace2Evil Warden problem
Point to door A and ask if door B is death. If he says yes then you know door C is freedom. If he says no then you know door B is freedom
Reasoning: If he says yes then he's either telling the truth (meaning doors A and C are freedom) or he's lying (meaning B and C are freedom). C is freedom in both cases
If he says no then he's either telling the truth (meaning doors A and B are freedom) or he's lying (meaning B and C are freedom). B is freedom in both cases
link to original post
I agree!
However, I think I need to rephrase my reasoning from " he's either telling the truth or he's lying" to "he's either telling the truth or he's giving a random answer". Because there's no way for him to answer "no" and be "lying", since this would mean both doors A and B are deathQuote: WizardQuote: Ace2Evil Warden problem
Point to door A and ask if door B is death. If he says yes then you know door C is freedom. If he says no then you know door B is freedom
Reasoning: If he says yes then he's either telling the truth (meaning doors A and C are freedom) or he's lying (meaning B and C are freedom). C is freedom in both cases
If he says no then he's either telling the truth (meaning doors A and B are freedom) or he's lying (meaning B and C are freedom). B is freedom in both cases
link to original post
I agree!
link to original post
I'm glad my life did not depend on this...not with a time limit anyway. This problem gave my brain a good workout today
Quote: Ace2However, I think I need to rephrase my reasoning from " he's either telling the truth or he's lying" to "he's either telling the truth or he's giving a random answer". Because there's no way for him to answer "no" and be "lying", since this would mean both doors A and B are deathQuote: WizardQuote: Ace2Evil Warden problem
Point to door A and ask if door B is death. If he says yes then you know door C is freedom. If he says no then you know door B is freedom
Reasoning: If he says yes then he's either telling the truth (meaning doors A and C are freedom) or he's lying (meaning B and C are freedom). C is freedom in both cases
If he says no then he's either telling the truth (meaning doors A and B are freedom) or he's lying (meaning B and C are freedom). B is freedom in both cases
link to original post
I agree!
link to original post
link to original post
If Door A is freedom, and:
(1) the answer is "Yes," then B is death, so A and C are freedom;
(2) the answer is "No," then B is freedom.
If Door A is death, then B and C are freedom no matter what the answer was.
In either case, if the answer is "Yes," then C is freedom, and if the answer is "No," then B is freedom.
For purposes of example, what is the probability of being able to last 100 even-money bets in double-zero roulette with a bankroll of 20 units?
Better yet, any formula to estimate the probability of lasting t bets, with a bankroll of b units, at a coin-flip game where wins pay even money and the probability of a winning flip is p. In the roulette example above, t=100, b=20, p=18/38.
Let's take comments over to to the RoR in baccarat thread.
Can someone prove why the RoR is double?
Quote: Ace2For a bet that follows the normal distribution exactly, the risk of ruin for a given bankroll and playing time is exactly double the probability of ending the session with a busted bankroll. For example, if you have a 63 unit bankroll and bet on 1,000 fair coin flips with an even money payout, your RoR is 4.62912 %. If you have unlimited bankroll, the probability of ending the session down more than 62 units is 2.31456%. Incidentally, a z-score calculator approximates the latter as 2.31726%
Can someone prove why the RoR is double?
link to original post
Surely this isnít true when the number of bets equals the limited bankroll. In that case, wouldnít the two probabilities be equal?
Quote: Ace2For a bet that follows the normal distribution exactly, the risk of ruin for a given bankroll and playing time is exactly double the probability of ending the session with a busted bankroll. For example, if you have a 63 unit bankroll and bet on 1,000 fair coin flips with an even money payout, your RoR is 4.62912 %. If you have unlimited bankroll, the probability of ending the session down more than 62 units is 2.31456%. Incidentally, a z-score calculator approximates the latter as 2.31726%
link to original post
I think I don't understand something. The 2.31456% probability doesn't seem to have anything to do with a 63-unit bankroll. So, why is it half of the RoR with a 63-unit bankroll?
Quote: Ace2For a bet that follows the normal distribution exactly, the risk of ruin for a given bankroll and playing time is exactly double the probability of ending the session with a busted bankroll. For example, if you have a 63 unit bankroll and bet on 1,000 fair coin flips with an even money payout, your RoR is 4.62912 %. If you have unlimited bankroll, the probability of ending the session down more than 62 units is 2.31456%. Incidentally, a z-score calculator approximates the latter as 2.31726%
Can someone prove why the RoR is double?
link to original post
How about this for the conceptual proof.
Fair coin flip has an EV of zero. After X trials, 50% you are up and 50% you are down if the starting bankroll is unlimited.
Now imagine a limited bankroll of $Y with X trials of $1 each. The RoR is whatever it is (doesnít matter what the formula for it is).
For the subset of possibilities where ruin is achieved on trial K (where K < X) imagine you instead have infinite money at that point but are down $Y. What is the probability that after additional trials of X - K that you will still be down at least $Y? 50% since every additional trial is EV of zero.
Therefore the risk of ruin is for X trials with $Y bankroll is double the risk of being down $Y with X trials and an infinite bankroll.
ETA: Note the even/odd issues with X - K so itís not always exactly 50% (just think about if X - K = 2 or 0). But where X - K is large, itís basically 50%.
If you bet on 1,000 flips, your expectation is to finish the session up/down zero units +/- 1000^.5, but there is a 2.31456% chance you'll finish down 63 units or more. There is a 2 * 2.31456% = 4.62912 % you will be down 63 or more units at any time during the 1,000 flips, which is your risk of ruin.Quote: WizardQuote: Ace2For a bet that follows the normal distribution exactly, the risk of ruin for a given bankroll and playing time is exactly double the probability of ending the session with a busted bankroll. For example, if you have a 63 unit bankroll and bet on 1,000 fair coin flips with an even money payout, your RoR is 4.62912 %. If you have unlimited bankroll, the probability of ending the session down more than 62 units is 2.31456%. Incidentally, a z-score calculator approximates the latter as 2.31726%
link to original post
I think I don't understand something. The 2.31456% probability doesn't seem to have anything to do with a 63-unit bankroll. So, why is it half of the RoR with a 63-unit bankroll?
link to original post
I selected 63 units because it's about 2 standard deviations, but you can pick any bankroll. For instance, a bankroll of 95 units has a RoR of 0.264552% and a 0.132276% chance (exactly half of RoR) of ending the session down 95 units or more.
WHY is it half? Answer correctly and you win this easy math puzzle
Quote: Ace2If you bet on 1,000 flips, your expectation is to finish the session up/down zero units, but there is a 2.31456% chance you'll finish down 63 units or more. There is a 2 * 2.31456% = 4.62912 % you will be down 63 or more units at any time during the 1,000 flips, which is your risk of ruin.
I selected 63 units because it's about 2 standard deviations, but you can pick any bankroll. For instance, a bankroll of 95 units has a RoR of 0.264552% and a 0.132276% chance (exactly half of RoR) of ending the session down 95 units or more.
WHY is it half? Answer correctly and you win this easy math puzzle
link to original post
Okay, thank you. The ball is in my court.
Quote: WizardQuote: Ace2If you bet on 1,000 flips, your expectation is to finish the session up/down zero units, but there is a 2.31456% chance you'll finish down 63 units or more. There is a 2 * 2.31456% = 4.62912 % you will be down 63 or more units at any time during the 1,000 flips, which is your risk of ruin.
I selected 63 units because it's about 2 standard deviations, but you can pick any bankroll. For instance, a bankroll of 95 units has a RoR of 0.264552% and a 0.132276% chance (exactly half of RoR) of ending the session down 95 units or more.
WHY is it half? Answer correctly and you win this easy math puzzle
link to original post
Okay, thank you. The ball is in my court.
link to original post
I think I answered it.
I think I follow your explanation, but I don't see how it demonstrates that the RoR is double the probability of finishing the session down more than your bankroll.Quote: unJonQuote: Ace2For a bet that follows the normal distribution exactly, the risk of ruin for a given bankroll and playing time is exactly double the probability of ending the session with a busted bankroll. For example, if you have a 63 unit bankroll and bet on 1,000 fair coin flips with an even money payout, your RoR is 4.62912 %. If you have unlimited bankroll, the probability of ending the session down more than 62 units is 2.31456%. Incidentally, a z-score calculator approximates the latter as 2.31726%
Can someone prove why the RoR is double?
link to original post
How about this for the conceptual proof.
Fair coin flip has an EV of zero. After X trials, 50% you are up and 50% you are down if the starting bankroll is unlimited.
Now imagine a limited bankroll of $Y with X trials of $1 each. The RoR is whatever it is (doesnít matter what the formula for it is).
For the subset of possibilities where ruin is achieved on trial K (where K < X) imagine you instead have infinite money at that point but are down $Y. What is the probability that after additional trials of X - K that you will still be down at least $Y? 50% since every additional trial is EV of zero.
Therefore the risk of ruin is for X trials with $Y bankroll is double the risk of being down $Y with X trials and an infinite bankroll.
ETA: Note the even/odd issues with X - K so itís not always exactly 50% (just think about if X - K = 2 or 0). But where X - K is large, itís basically 50%.
link to original post
Quote: Ace2I think I follow your explanation, but I don't see how it demonstrates that the RoR is double the probability of finishing the session down more than your bankroll.Quote: unJon
For the subset of possibilities where ruin is achieved on trial K (where K < X) imagine you instead have infinite money at that point but are down $Y. What is the probability that after additional trials of X - K that you will still be down at least $Y? 50% since every additional trial is EV of zero.
Therefore the risk of ruin is for X trials with $Y bankroll is double the risk of being down $Y with X trials and an infinite bankroll.
link to original post
link to original post
(edited)
On an infinite bankroll, half the time you lose before you win some back.
You can't do that on a finite bankroll.
I do tend to agree that it's not quite exactly double (probably due to house edge), but it should be a reasonable approximation if you're trying to decide to play with dozens, hundreds, or thousands of units for a certain number of resolutions.
Without a house edge it is exactly doubleQuote: DieterQuote: Ace2I think I follow your explanation, but I don't see how it demonstrates that the RoR is double the probability of finishing the session down more than your bankroll.Quote: unJon
For the subset of possibilities where ruin is achieved on trial K (where K < X) imagine you instead have infinite money at that point but are down $Y. What is the probability that after additional trials of X - K that you will still be down at least $Y? 50% since every additional trial is EV of zero.
Therefore the risk of ruin is for X trials with $Y bankroll is double the risk of being down $Y with X trials and an infinite bankroll.
link to original post
link to original post
(edited)
On an infinite bankroll, half the time you lose before you win some back.
You can't do that on a finite bankroll.
I do tend to agree that it's not quite exactly double (probably due to house edge), but it should be a reasonable approximation if you're trying to decide to play with dozens, hundreds, or thousands of units for a certain number of resolutions.
link to original post
Quote: Ace2Without a house edge it is exactly double
link to original post
Believable. Also believable that I got interested in the discussion of this particular problem, forgot this was the EMP thread, that the thread's general standard for formal proof has not been met on this one, and I am not going to earn a beer.
Quote: Ace2I think I follow your explanation, but I don't see how it demonstrates that the RoR is double the probability of finishing the session down more than your bankroll.Quote: unJonQuote: Ace2For a bet that follows the normal distribution exactly, the risk of ruin for a given bankroll and playing time is exactly double the probability of ending the session with a busted bankroll. For example, if you have a 63 unit bankroll and bet on 1,000 fair coin flips with an even money payout, your RoR is 4.62912 %. If you have unlimited bankroll, the probability of ending the session down more than 62 units is 2.31456%. Incidentally, a z-score calculator approximates the latter as 2.31726%
Can someone prove why the RoR is double?
link to original post
How about this for the conceptual proof.
Fair coin flip has an EV of zero. After X trials, 50% you are up and 50% you are down if the starting bankroll is unlimited.
Now imagine a limited bankroll of $Y with X trials of $1 each. The RoR is whatever it is (doesnít matter what the formula for it is).
For the subset of possibilities where ruin is achieved on trial K (where K < X) imagine you instead have infinite money at that point but are down $Y. What is the probability that after additional trials of X - K that you will still be down at least $Y? 50% since every additional trial is EV of zero.
Therefore the risk of ruin is for X trials with $Y bankroll is double the risk of being down $Y with X trials and an infinite bankroll.
ETA: Note the even/odd issues with X - K so itís not always exactly 50% (just think about if X - K = 2 or 0). But where X - K is large, itís basically 50%.
link to original post
link to original post
Let me try to explain it this way:
Letís stick to coin flips. If I have an infinite bankroll and am playing 1000 trials, half the time I will end ahead and half the time I will end behind. (This ignores the times I will end at exactly a tie. Thatís fine for now, but we can come back to it.)
Now letís say I lose the first coin flip so am at -1. I now am playing a 999 trial game with an infinite bankroll. So half of the remaining time I will end up ahead of -1 and half worse than -1. (Note no possibility of being at exactly -1 anymore because there are an odd number of trials left.)
All agreed so far?
Now imagine with my infinite bankroll that at some point during the 1,000 trials I first reach -63. How often does that occur? It occurs exactly as frequently as the RoR with a 63 bankroll and 1,000 trials. They are identical paths (or Markov chains) to get to that point of -63 the first time.
So X% of the time with an infinite bankroll you end up for the first time at -63 at some point during the 1,000 trials. Where X% is exactly the RoR for 63 bankroll. It might have happened at trial 63 or trial 1,000 or somewhere in between. Letís assume itís somewhere in between.
What is the probability now that we are at -63 and have an infinite bankroll and some number of trials left to get to 1,000 that we will do worse than -63? 50%
So 50% of X% of the time with an infinite bankroll you end up at -63 at the end of 1,000 trials. Thatís 1/2 of the RoR with a 63 bankroll.
You are convinced which four teams will make it to the Final Four.
How many different brackets do you need to fill out in order to guarantee that, if all four do make it to the Final Four, you will have a perfect one - i.e. one in which you correctly pick the winners of all 63 games? You may assume that you know the winners of the four "First Four" games in advance. (Yes, the women have 68 teams this year. Starting next year, they will have their own version of Dayton, but this year, each women's First Four game will be played at the site where the winner would play its next game. Oh, and don't call them "Play-Ins"; that term means something else.)
On Survivor last week they had the following diagram. The object was to find the number of trianlges.
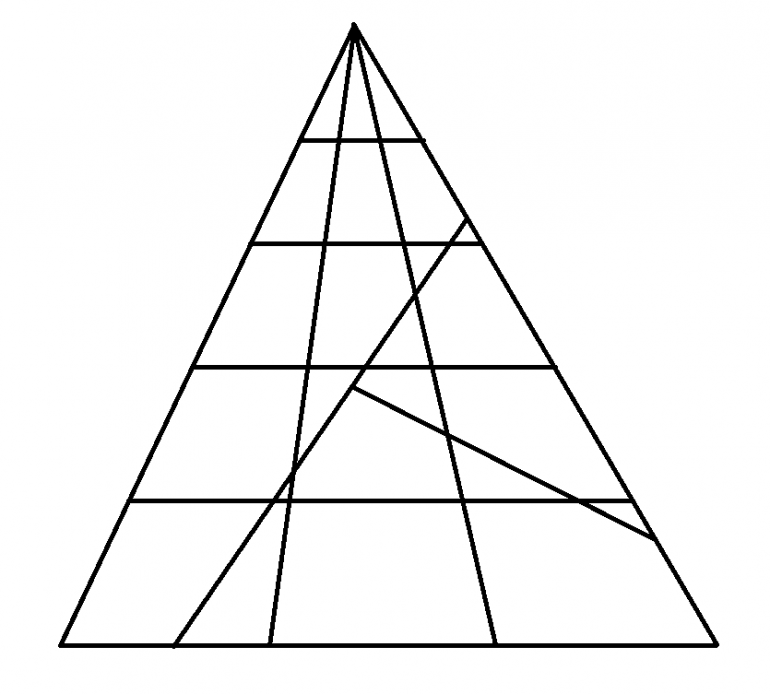
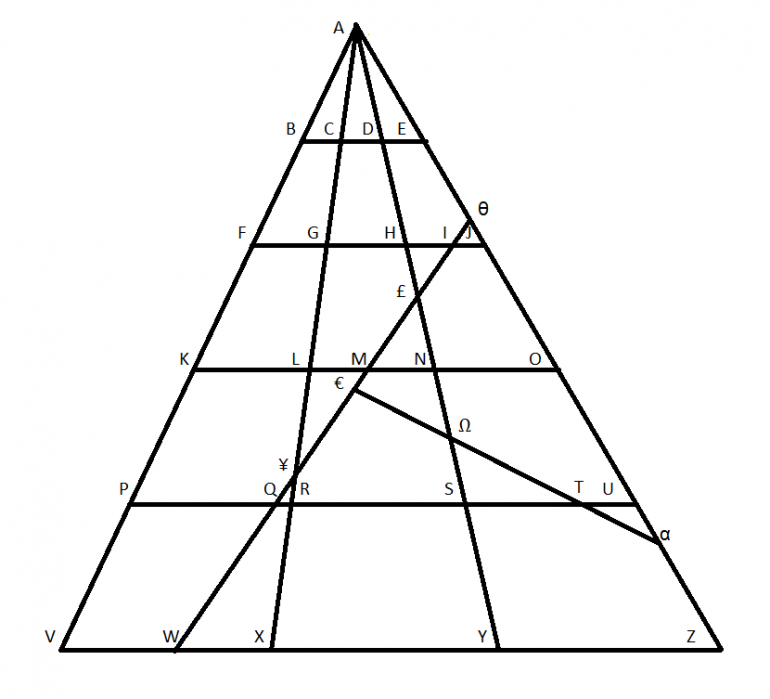
2^47???
Don't have to pick any games with the final four teams up to the final four. So # games to pick in rounds are
(28+12+4+0)=44
Then have to pick 3 more games (both semis and thee championship) since you say final four are know but NOT that you know the outcome of final four.
EDIT: Updated = 51????
Originally.....
I got 49??
with A at top there are 6 for each horizontal line (3 small, 2 double and one triple) (e.g. ABC, ACD, ADE, ABD, ACE, ABE) x 5 horizontal lines = 30
For line Theta to W I get 17** that have one side along the Theta W line
Then I also see Alpha U T and TS Omega from addition of line through Alpha (but not already counted above)*****
30+17+2 = 49???
***** Plus. Alpha - Omega - A
** Plus one more for Theta to W = 18
Edited Total = 30+18+3 = 51


