Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
Quote: WizardQuote: DRichSpeaking of cuboids, I am moving shortly and rented a pod from U-haul.
link to original post
If you have a yard sale, please give me first dibs.
link to original post
Sorry, We have given almost everything away.
The correct answer is YES. If it doesn't fit in the box I don't want it and don't need it. Sorry, I didn't mean to hijack your thread. I am out.Quote: DieterQuote: DRich
Will I be able to get everything that I want and need in that box for moving?
link to original postNo.
link to original post
Quote: ThatDonGuy
General terms answer:
Let A, B, C be the measures of the three perimeters
Let the three side lengths be X, Y, and Z, such that A = 2X + 2Y, B = 2X + 2Z, and C = 2Y + 2Z.
A + B + C = 4 (X + Y + Z)
X + Y + Z = (A + B + C) / 4
X = (A + B + C) / 4 - C / 2
Y = (A + B + C) / 4 - B / 2
Z = (A + B + C) / 4 - A / 2
For A = 12, B = 16, C = 20:
(A + B + C) / 4 = 12
X = 12 - 10 = 2
Y = 12 - 8 = 4
Z = 12 - 6 = 6
Volume = 48
For A = 12, B = 16, C = 24:
(A + B + C) / 4 = 13
X = 13 - 12 = 1
Y = 13 - 8 = 5
Z = 13 - 6 = 7
Volume = 35
Cuboid A has the greater volume
Quote: WizardRE: cuboid puzzle
I agree with Don.
Correct!!
----------------------------------
US students were ranked 31st in the world at math tests.
Well, at least we're in the top 10.
Quote: DRichThe correct answer is YES. If it doesn't fit in the box I don't want it and don't need it. Sorry, I didn't mean to hijack your thread. I am out.Quote: DieterQuote: DRich
Will I be able to get everything that I want and need in that box for moving?
link to original postNo.
link to original post
link to original post
My apologies, good sir. Congratulations on reducing your belongings that far.
Quote: Ace2Another easy math puzzle:
In the game of craps, what is the probability that all six points are won (at least once) over the course of one hour?
Assume thirty passline bets resolved per hour.
link to original post
I don't know about "easy"; I had to use a Markov chain, as I couldn't figure out a Poisson method that had the limiting condition of 30 passline bets resolved.
I assume that "passline bets resolved" includes naturals and craps on the comeout.
354,353,717,689,729,495,346,499,790,918,404,219,858,091,437,606,878,240,178,848,967,360,063,110,300,788,197,457
/ 3,013,786,353,904,990,101,334,978,123,730,459,697,586,091,109,517,660,969,708,290,048,000,000,000,000,000,000,000
or about 1 / 8.505
Though I agree with your final answer, I’d like to see a formulaic solution for full creditQuote: ThatDonGuyQuote: Ace2Another easy math puzzle:
In the game of craps, what is the probability that all six points are won (at least once) over the course of one hour?
Assume thirty passline bets resolved per hour.
link to original post
I don't know about "easy"; I had to use a Markov chain, as I couldn't figure out a Poisson method that had the limiting condition of 30 passline bets resolved.
I assume that "passline bets resolved" includes naturals and craps on the comeout.
354,353,717,689,729,495,346,499,790,918,404,219,858,091,437,606,878,240,178,848,967,360,063,110,300,788,197,457
/ 3,013,786,353,904,990,101,334,978,123,730,459,697,586,091,109,517,660,969,708,290,048,000,000,000,000,000,000,000
or about 1 / 8.505
link to original post
Hint: The solution does not use Poisson or calculus. To my knowledge, that method only works when integrating from zero to infinity (over all time). So it would not apply to this problem that has a limiting factor of thirty trials
Quote: Ace2Though I agree with your final answer, I’d like to see a formulaic solution for full credit
So would I. I have a feeling that, with the limiting condition, it's a little but outside of my current math pay grade.
Does anyone want more time?Quote: Ace2Another easy math puzzle:
In the game of craps, what is the probability that all six points are won (at least once) over the course of one hour?
Assume thirty passline bets resolved per hour.
link to original post
It’s well within your pay gradeQuote: ThatDonGuyQuote: Ace2Though I agree with your final answer, I’d like to see a formulaic solution for full credit
So would I. I have a feeling that, with the limiting condition, it's a little but outside of my current math pay grade.
link to original post
Quote: acesideMy second attempt:
Let x=days needed for sheep to consume the 2nd acre of grass;
Let g=growth rate of grass;
let c= consume rate of grass by sheep.
Then we have
2+3g=3c;
2+3g+x g =x c
Solving this set of two equations when setting g=1, we get
x=7.5 days.
link to original post
Let's come back to the sheep puzzle. As a reminder, here is the original wording.
I agree that the answer here is correct, but I am surprised because I don't agree with the solution. This solution seems to ignore my condition that once a blade of grass is eaten, it does not grow back. Perhaps the error cuts equally in both the first and second acres, which is why the answer is right.
Here is my solution (PDF).
For each resolution, the chance of winning with a point of four, five and six is 55/1980, 88/1980 and 125/1980 respectively and the chance of winning with a point of ten, nine and eight is the same respectivelyQuote: Ace2Another easy math puzzle:
In the game of craps, what is the probability that all six points are won (at least once) over the course of one hour?
Assume thirty passline bets resolved per hour.
link to original post
So, using inclusion-exclusion, the probability of NOT winning all six points in thirty resolutions is:
{(1925^30 + 1892^30 + 1855^30)*2
- (4*[1837^30 + 1800^30 + 1767^30] + 1870^30 + 1804^30 + 1730^30)
+ (8*1712^30 + 2*[1782^30 + 1745^30 + 1749^30 + 1679^30 + 1675^30 + 1642^30])
- (1694^30 + 1620^30 + 1554^30 + 4*[1657^30 + 1624^30 + 1587^30])
+ (1569^30 + 1532^30 + 1499^30)*2
- (1444^30)} / 1980^30
=~ 88.24%.
Therefore the probability of winning all six points is 1 - 0.8824 or approximately 11.76%
For those of you not familiar with inclusion-exclusion, the formula sums the c(6,1) ways that one point can be missed in thirty trials, then subtracts the c(6,2) ways that two points can be missed, then adds the c(6,3) ways that three points can be missed, then subtracts the c(6,4) ways that four points can be missed, then adds the c(6,5) ways that five points can be missed, then subtracts the c(6,6) ways that six points can be missed. As an example, in the c(6,2) term, 4*(1837/1980)^30 represents the ways that 4&5, 4&9, 5&10 and 9&10 can be missed. 1980 - 55 - 88 = 1837
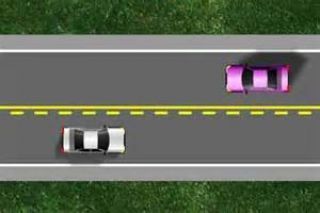
Two cars (A and B) start at the starting line at the same time on a 3-mile long track, going in opposite directions. As they drive around the course, they pass each other many times. Exactly one hour after starting, they pass each other for the 33rd time. At this point car A has completed exactly 20 laps.
What is the average speed of Car B?
Quote: GialmereHere's an easy, Easy Monday puzzle...
Two cars (A and B) start at the starting line at the same time on a 3-mile long track, going in opposite directions. As they drive around the course, they pass each other many times. Exactly one hour after starting, they pass each other for the 33rd time. At this point car A has completed exactly 20 laps.
What is the average speed of Car B?
link to original post
We let Car B speed= vb.
After 33 passes in one hour, both cars ran 1x(va+vb)=33x3, miles.
Solving this equation, we get Car B speed vb=39 mile/hour.
Quote: GialmereWhat is the average speed of Car B?
link to original post
distance = rate*time
Let's define some terms:
x = distance traveled by A until the first passing point.
t = time elapsed at first passing point.
r = speed of B.
If A travels a 3-mile long track 20 times in an hour, then his speed is 60 mph.
We know:
3-x = r*t
x = 60*(3-x)/r
Two equations and two unknowns easily leads to r = 39.
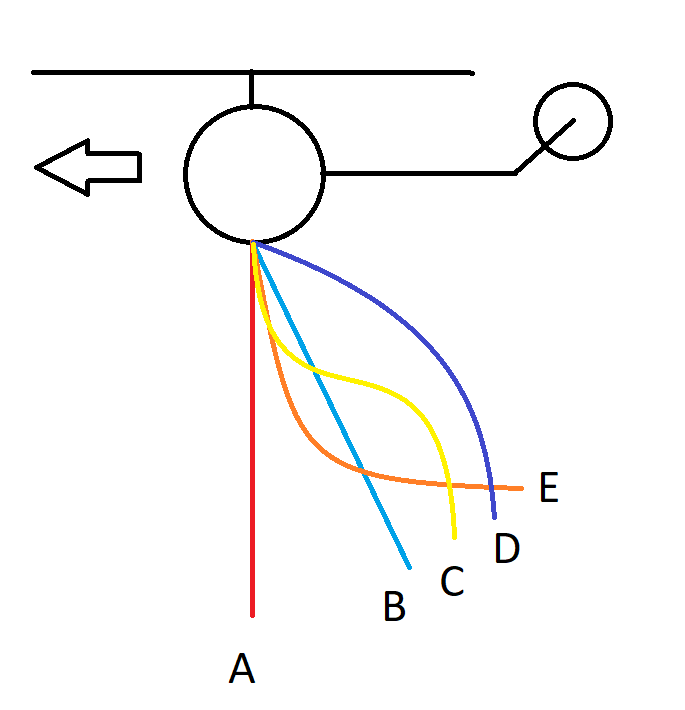
The helicopter above is traveling at a constant rate and altitude. There is no wind. It is pulling a heavy chain. What shape will the chain make?
Quote: WizardIf I may presume business finished with G's puzzle, here is a physics one. I know there is a video on this, so please don't just post a URL to that. Try to argue your answer in your own words.
The helicopter above is traveling at a constant rate and altitude. There is no wind. It is pulling a heavy chain. What shape will the chain make?
link to original post
Is there air resistance? Or traveling in vacuum?
Quote: WizardIf I may presume business finished with G's puzzle, here is a physics one. I know there is a video on this, so please don't just post a URL to that. Try to argue your answer in your own words.
The helicopter above is traveling at a constant rate and altitude. There is no wind. It is pulling a heavy chain. What shape will the chain make?
link to original post
Quote: unJonIs there air resistance? Or traveling in vacuum?
link to original post
There's air resistance.
Quote: acesideNewton’s First Law: a body in motion stays in motion fully relaxed. So, the answer is A, because it’s center of mass is at the lowest possible position.
link to original post
Does this consider my condition the helicopter is moving? I said it's traveling a constant rate. That rate is not zero, but a normal flying speed for a helicopter.
Quote: WizardQuote: acesideNewton’s First Law: a body in motion stays in motion fully relaxed. So, the answer is A, because it’s center of mass is at the lowest possible position.
link to original post
Does this consider my condition the helicopter is moving? I said it's traveling a constant rate. That rate is not zero, but a normal flying speed for a helicopter.
link to original post
Oh, I misunderstood. I thought you meant “traveling at a constant rate” is the same as “traveling at a constant speed.” You can say “traveling at a constant acceleration,” which means “speeding up at a constant rate.” If the helicopter travels at a constant acceleration, the answer must not be A.
The main problem with this question is that a helicopter cannot fly without air. This makes the situation complicated!
Quote: acesideOh, I misunderstood. I thought you meant “traveling at a constant rate” is the same as “traveling at a constant speed.”
link to original post
I did mean that. The next time I ask this I'll say traveling at a constant speed.
Quote: acesideQuote: WizardIf I may presume business finished with G's puzzle, here is a physics one. I know there is a video on this, so please don't just post a URL to that. Try to argue your answer in your own words.
The helicopter above is traveling at a constant rate and altitude. There is no wind. It is pulling a heavy chain. What shape will the chain make?
link to original postNewton’s First Law: a body in motion stays in motion fully relaxed. So, the answer is A, because it’s center of mass is at the lowest possible position.
link to original post
I disagree.
Quote: acesideWe know Car A speed va=3*20/1= 60 mile/hour.
We let Car B speed= vb.
After 33 passes in one hour, both cars ran 1x(va+vb)=33x3, miles.
Solving this equation, we get Car B speed vb=39 mile/hour.
link to original post
Quote: Wizard
distance = rate*time
Let's define some terms:
x = distance traveled by A until the first passing point.
t = time elapsed at first passing point.
r = speed of B.
If A travels a 3-mile long track 20 times in an hour, then his speed is 60 mph.
We know:
3-x = r*t
x = 60*(3-x)/r
Two equations and two unknowns easily leads to r = 39.
link to original post
Correct!
--------------------------------------
Quote: WizardThe chain is heavy. You may assume the thickness of those used in a swing set.
link to original post
Quote: acesideIn that case, the answer must be B, because Newton’s First Law states that a body in motion stays in motion fully relaxed. The air pressure only lifts up the center of mass of the chain without causing any defamation to it.
link to original post
I agree the answer is B. I wouldn't have explained it that way, but I'm not saying your explanation is wrong either.
Here is the video that inspired this puzzle.
direct: https://www.youtube.com/watch?v=q-_7y0WUnW4
I started this thread because the forum was previously swamped with math puzzle threads.
I'd like to suggest that anyone with a difficult puzzle make a separate thread for it. Let's try to remember the thread title and keep this thread for only "easy" puzzles.
Thank you.

An ordinary die is rolled until the running total of the rolls first exceeds 12.
What is the most likely final total that will be obtained?
Quote: GialmereAn ordinary die is rolled until the running total of the rolls first exceeds 12.
What is the most likely final total that will be obtained?
link to original post
The most likely final total is 13
If the current total is 12, then a final result of 13, 14, 15, 16, 17, or 18 is equally likely.
If it is 11, then a final result of 13, 14, 15, 16, or 17 is equally likely, as is an "active" result of 12.
If it is 10, then a final result of 13, 14, 15, or 16 is equally likely, as are "active" results of 11 or 12.
If it is 9, then a final result of 13, 14, or 15 is equally likely, as are "active" results of 10, 11, or 12.
If it is 8, then a final result of 13 or 14 is equally likely, as are "active" results of 9, 10, 11, or 12.
If it is 7, then a final result of 13 is as equally likely as "active" results of 8, 9, 10, 11, or 12.
I get 13. Here is a table showing the probability of each possible final total.
| Total | Probability |
|---|---|
| 13 | 0.290830 |
| 14 | 0.230791 |
| 15 | 0.188524 |
| 16 | 0.143842 |
| 17 | 0.097114 |
| 18 | 0.048899 |
| Average | 14.690219 |
Quote: ThatDonGuy
The most likely final total is 13
If the current total is 12, then a final result of 13, 14, 15, 16, 17, or 18 is equally likely.
If it is 11, then a final result of 13, 14, 15, 16, or 17 is equally likely, as is an "active" result of 12.
If it is 10, then a final result of 13, 14, 15, or 16 is equally likely, as are "active" results of 11 or 12.
If it is 9, then a final result of 13, 14, or 15 is equally likely, as are "active" results of 10, 11, or 12.
If it is 8, then a final result of 13 or 14 is equally likely, as are "active" results of 9, 10, 11, or 12.
If it is 7, then a final result of 13 is as equally likely as "active" results of 8, 9, 10, 11, or 12.
Quote: Wizard
I get 13. Here is a table showing the probability of each possible final total.
Total Probability 13 0.290830 14 0.230791 15 0.188524 16 0.143842 17 0.097114 18 0.048899 Average 14.690219
Correct!
-------------------------------------
The cops raided my house and carted off all my books on algebra, trigonometry and calculus, plus dice and other probability demo stuff.
They claimed it was all weapons of math instruction.
Quote: GialmereYes. The knee-jerk response would be "14" based on an average die roll. Due to the way the way the puzzle is worded, however, "13" is correct by several percentage points.
There's a reason that the only result in Trente et Quarante (or, in Italian, Trenta e Quaranta) where the house has an advantage is 31-31.

?/?? + ?/?? + ?/?? = 1
Each of three fractions has a one-digit numerator and a two-digit denominator. The three fractions together add up to one.
Place the nine digits 1-9 into the fractions to make the equation correct.
I got one:Quote: Gialmere
?/?? + ?/?? + ?/?? = 1
Each of three fractions has a one-digit numerator and a two-digit denominator. The three fractions together add up to one.
Place the nine digits 1-9 into the fractions to make the equation correct.
link to original post
You use "3" twice and don't have "5".Quote: acesideI got one:Quote: Gialmere
?/?? + ?/?? + ?/?? = 1
Each of three fractions has a one-digit numerator and a two-digit denominator. The three fractions together add up to one.
Place the nine digits 1-9 into the fractions to make the equation correct.
link to original post7/14+8/32+9/36=1
link to original post
Quote: WizardThanks, I wasted about an hour on this by brute force trial and error and never found an answer. So I cheated and searched on it. Give me zero credit.
link to original post
So did I - well, "brute force" as in "get my computer to generate all 362,880 permutations of 1-9," and I did get a solution:
I got one:Quote: aceside
link to original post
You used a 3 twice.
Quote: ThatDonGuySo did I - well, "brute force" as in "get my computer to generate all 362,880 permutations of 1-9," and I did get a solution:
9/12 + 5/34 + 7/68 = 1
link to original post
Did you sort them in lexographic order?
Quote: Gialmere
?/?? + ?/?? + ?/?? = 1
Each of three fractions has a one-digit numerator and a two-digit denominator. The three fractions together add up to one.
Place the nine digits 1-9 into the fractions to make the equation correct.
link to original post
In my early attempts: I realized the first number must be 9 divided by a very low denominator (either 12 or 13), and the second and third numbers must have denominators that are multiples of the first fraction's denominators, preferably with the 8 or possibly 7 in the numerator of the fraction with the 2nd smallest denominator.
Thus, I tried 9/12, 8/36 and 5/72 -which yields a sum larger than 1. (12*9 +4*8+ 2*5)/144 = 151/144 Too large!
After a long time, I realized that since 9/12 is 0.75, the other two denominators need not be multiples of 12, they only must be such that the last two fractions sum to 0.25. So the 2nd denominator could be a wide range of numbers and the third denominator must be a multiple of the 2nd denominator.
And, after more fumbling I saw that the trick was also to use the lowest remaining numerator on the 2nd fraction, thus, I stumbled onto 9/12 and 5/34 and 7/68 = 0.75 + (5*2+ 7)/68 = 0.75 + 17/68 =1
This took me roughly 70 minutes! Very, very hard. I was very slow to realize that the 2nd and third denominators need not be a multiple of the first denominator.
Quote: ThatDonGuySo did I - well, "brute force" as in "get my computer to generate all 362,880 permutations of 1-9," and I did get a solution:
9/12 + 5/34 + 7/68 = 1
Quote: gordonm888
In my early attempts: I realized the first number must be 9 divided by a very low denominator (either 12 or 13), and the second and third numbers must have denominators that are multiples of the first fraction's denominators, preferably with the 8 or possibly 7 in the numerator of the fraction with the 2nd smallest denominator.
Thus, I tried 9/12, 8/36 and 5/72 -which yields a sum larger than 1. (12*9 +4*8+ 2*5)/144 = 151/144 Too large!
After a long time, I realized that since 9/12 is 0.75, the other two denominators need not be multiples of 12, they only must be such that the last two fractions sum to 0.25. So the 2nd denominator could be a wide range of numbers and the third denominator must be a multiple of the 2nd denominator.
And, after more fumbling I saw that the trick was also to use the lowest remaining numerator on the 2nd fraction, thus, I stumbled onto 9/12 and 5/34 and 7/68 = 0.75 + (5*2+ 7)/68 = 0.75 + 17/68 =1
This took me roughly 70 minutes! Very, very hard. I was very slow to realize that the 2nd and third denominators need not be a multiple of the first denominator.
Correct!!
Very good!
Apologies to the board. This came from one of the easier puzzle sources and it looked like it could be fiddle solved in only 10 or 20 minutes. (Admittedly the site does have some toughies.)
-----------------------------------------------
void three_fraction(void)
{
int i, x_max, y_max, temp_array[100], hold, pt;
int lex_array[] = { 1,2,3,4,5,6,7,8,9 };
int num_elements = sizeof(lex_array) / sizeof(lex_array[0]);
int count = 0;
bool stop = false;
double tot3;
cerr << "Number of elements =\t" << num_elements << "\n";
do
{
count++;
tot3 = (double)lex_array[0] / (double)(10 * lex_array[1] + lex_array[2]);
tot3 += (double)lex_array[3] / (double)(10 * lex_array[4] + lex_array[5]);
tot3 += (double)lex_array[6] / (double)(10 * lex_array[7] + lex_array[8]);
if (tot3 == 1.0)
{
cerr << count << "\t";
cerr << lex_array[0] << "/" << lex_array[1] << lex_array[2] << " + ";
cerr << lex_array[3] << "/" << lex_array[4] << lex_array[5] << " + ";
cerr << lex_array[6] << "/" << lex_array[7] << lex_array[8] << "\n";
}
x_max = -1;
for (i = 0; i < (num_elements - 1); i++)
{
if (lex_array < lex_array[i + 1])
x_max = i;
}
if (x_max >= 0)
{
y_max = 0;
for (i = x_max + 1; i < num_elements; i++)
{
if (lex_array[x_max] < lex_array)
y_max = i;
}
hold = lex_array[x_max];
lex_array[x_max] = lex_array[y_max];
lex_array[y_max] = hold;
if (x_max + 1 < num_elements - 1) // reverse
{
for (i = x_max + 1; i < num_elements; i++)
{
temp_array = lex_array;
}
pt = 0;
for (i = x_max + 1; i < num_elements; i++)
{
lex_array = temp_array[num_elements - 1 - pt];
pt++;
}
}
}
else
stop = true;
} while (stop == false);
}
p.s. G, I would not consider this an "easy" problem. Let's try to get in the habit of making new threads for intermediate and harder problems.
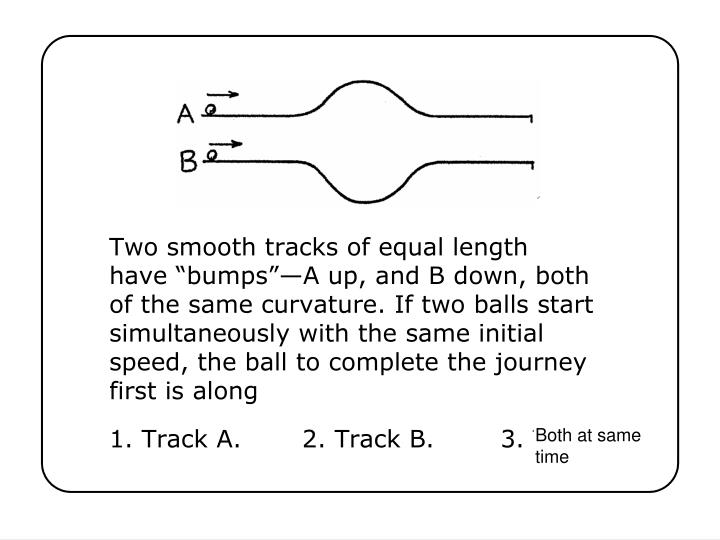
The distance travelled by the two balls is the same, so the only difference is the velocity (or speed). Since there is no force the energy would remain constant, thus as ball A rises, it gains potential energy so will lose kinetic energy, thus it will slow down. For ball B, it loses potential energy so gains kinetic energy, thus it speeds up down into the valley. So at the mid point ball A is going slower than ball B, hence ball B will get to the finish earlier.
An easier way to think of it is if a driver of a car goes up a hill they tend to slow down and then speed up downhill.
Quote: GialmereClassic Physics...
link to original post
On another note, this problem is related to Brachistochrone curve, the track for the least possible traveling time.
When I first saw it, I answered, "3, since the amount that it goes up equals the amount that it goes down in both cases."
However, I am pretty sure the answer is 2, because the velocity both when it starts the upward path and when it starts the downward path is greater in B than in A, so while the final velocities may be the same, the time it takes is less in B.
The answer is B. Both courses will result in the same final velocity, which is equal to the initial velocity in this frictionless example.. But in course A the ball is decelerated then reaccelerated to the original speed, whereas in B the ball is accelerated to a higher speed and then decelerated to a lower speed. The integral over speed = v(t) will yield a higher average speed for course B, and thus the Ball in B will arrive first.
Note, I am assuming the speeds are all low relative to the speed of light and thus relativistic concerns are not a factor, lol.
Quote: GialmereClassic Physics...
link to original post
While A and B are traveling on the flat regions, they are both going at the same speed. So, A's and B's flat regions' times would be equal. So, we can ignore the flat regions.
To make the problem an "easy" problem, realize that a movie of the experiment would be almost the same going forward and backward. The only difference would be the backward movie would be a mirror image of the forward movie.
In other words, the time for B to go down the hill equals the time for B to go up the hill. And the same applies for A. But of course, B takes less time to go down the hill than A does to go up the hill because B is speeding up while A is slowing down.
So, B would definitely complete the course before A.


