Easy math puzzles

Threads: 43
Posts: 2871

Joined: Oct 19, 2009

October 14th, 2021 at 6:11:50 PM permalink

Quote: GM
Quote: teliot
The question about N! not being a perfect square for N >= 2 leads to a question that I don't know the answer to. Here goes.

For any integer N, consider the list of all primes that are in the half-open interval (N/2,N]. Call them p1, p2, p3 ... , pk. The question is, for which N is N!/(p1*p2*p3*...*pk) a perfect square? In other words, divide N! by all the primes greater than N/2 and less than or equal to N (the Bertrand's Postulate primes) and ask if what's leftover is a perfect square.

Here are the five examples I found searching N <= 22 (the largest N for which Excel accurately computes N!).

With N = 6, then we divide 6! by 5 and 6!/5 = 144 is a perfect square.
With N = 7, then we divide 7! by 5*7 = 35 and get 7!/35 = 144, again a perfect square.
With N = 10, then we divide 10! by 7 (the only prime in the interval (5,10]) and get 10!/7 = 518400 = 720^2 is a perfect square.
With N = 11, then we divide 11! by 11*7 and again get 10!/7 = 518400 = 720^2.
With N = 20, then we divide 20! by 19*17*13*11 and get 52672757760000 = 7257600^2.

Any others? Infinitely many? This isn't in the OEIS (at least that I can find).
link to original post

There is a paper by Jitsuro Nagura, which proves that for any real number x≥9, there exists a prime p such that x≤p<4x/3. If N≥35, we can apply this theorem with x=(N+1)/4 to obtain that there exists a prime p such that (N+1)/4≤p<(N+1)/3. Then p>N/4 clearly, and 3p<N+1, so 3p≤N, because 3p and N are integers, therefore p≤N/3.The only numbers among 1,2,...,N which are divisible by p are p, 2p and 3p, so N! is divisible by p^3 but not by p^4. After factoring out the primes between N and 2N, the resulting number will still be divisible by p^3, but not by p^4, so it cannot be a square.

This means that if N! divided by the product of primes in (N/2,N] is a square then N≤34. It is easy to check that the only solutions are N=2,3,6,7,10,11,20.
link to original post

An elegant and simple argument. Many thanks!

This reminds me of a theorem I have long since forgotten, an improvement on Bertrand's Postulate that follows from the PNT, that for any e > 0 there is a positive integer N such that for all n > N, there exists a prime p with n <= p < (1+e)n. The result you quoted was this bound N being explicitly computed when e equals 1/3.

Again fabulous work.

By the way, I tried to look up your reference, Wikipedia pointed to this result by Nagura: there is always a prime between n and 6/5*n for n >= 25. I couldn't find the result in the paper you referenced. But your proof holds, we would just have to run the exhaustive search out a bit further.

Last edited by: teliot on Oct 14, 2021

Climate Casino: https://climatecasino.net/climate-casino/

ben771williams

ben771williams

Threads: 1
Posts: 21

Joined: Oct 11, 2021

October 15th, 2021 at 5:18:25 AM permalink

here's another puzzle that's worthy of a beer

GM

Threads: 0
Posts: 49

Joined: Jun 16, 2021

Thanked by

October 15th, 2021 at 5:45:00 AM permalink

Quote: teliot

By the way, I tried to look up your reference, Wikipedia pointed to this result by Nagura: there is always a prime between n and 6/5*n for n >= 25. I couldn't find the result in the paper you referenced. But your proof holds, we would just have to run the exhaustive search out a bit further.
link to original post

There is a link on that page to download the whole paper, the statement of the theorem is at the bottom of the penultimate page.

teliot

Threads: 43
Posts: 2871

Joined: Oct 19, 2009

October 15th, 2021 at 5:50:58 AM permalink

Quote: GM
Quote: teliot

By the way, I tried to look up your reference, Wikipedia pointed to this result by Nagura: there is always a prime between n and 6/5*n for n >= 25. I couldn't find the result in the paper you referenced. But your proof holds, we would just have to run the exhaustive search out a bit further.
link to original post

There is a link on that page to download the whole paper, the statement of the theorem is at the bottom of the penultimate page.
link to original post

Okay -- found the download button and the theorem. For reference:

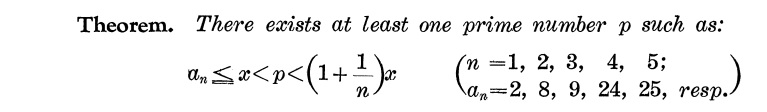
By the way, one consequence of an easy generalization of your argument is that for any integer k there exists an integer N such that for n > N there is a prime p so that p^k exactly divides n!.

Last edited by: teliot on Oct 15, 2021

Climate Casino: https://climatecasino.net/climate-casino/

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

October 18th, 2021 at 7:48:42 AM permalink

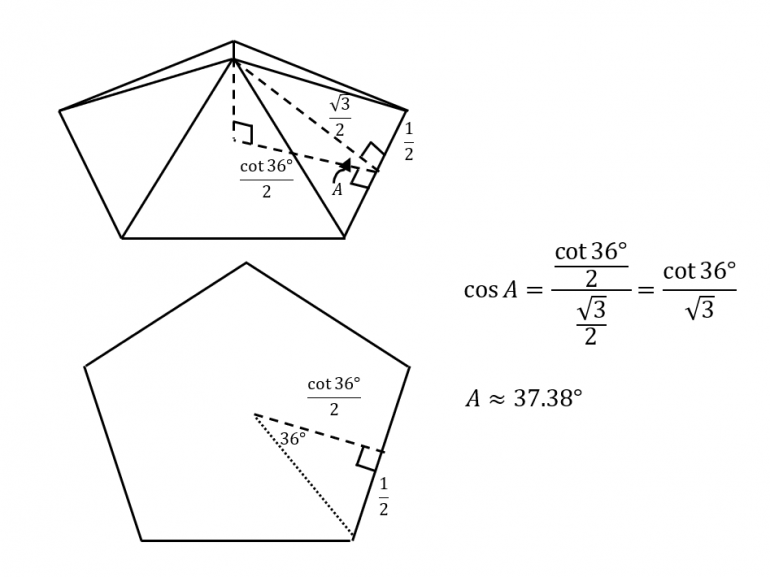
Consider a pyramid with a base of a regular N-gon. All other sides are triangles and every edge is of unit length.

1) What is the maximum N?

2) What is the angle between the base and a side?

3) What is the angle between two adjacent sides?

Have you tried 22 tonight? I said 22.

aceside

aceside

Threads: 2
Posts: 591

Joined: May 14, 2021

Thanked by

October 18th, 2021 at 5:59:24 PM permalink

Quote: Gialmere

Consider a pyramid with a base of a regular N-gon. All other sides are triangles and every edge is of unit length.

1) What is the maximum N?

2) What is the angle between the base and a side?

3) What is the angle between two adjacent sides?
link to original post

Apparently N=5, because when N=6, that pyramid will be flat.

Wizard
Administrator

Threads: 1520
Posts: 27119

Joined: Oct 14, 2009

Thanked by

October 18th, 2021 at 6:56:26 PM permalink

1. 5. At six, the pyramid would be flat. I'm not sure if that counts as a pyramid.
2. I'll bother to answer that if you confirm my answer of 5.
3. Based on a pentagonal base, 108.

I have a feeling I am not understanding the question correctly.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ChesterDog

ChesterDog

Threads: 9
Posts: 1730

Joined: Jul 26, 2010

Thanked by

October 18th, 2021 at 7:09:47 PM permalink

Quote: Gialmere

Consider a pyramid with a base of a regular N-gon. All other sides are triangles and every edge is of unit length.

...
2) What is the angle between the base and a side?

...
link to original post

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

October 18th, 2021 at 8:03:37 PM permalink

Quote: aceside

Apparently N=5, because when N=6, that pyramid will be flat.

Quote: Wizard

1. 5. At six, the pyramid would be flat. I'm not sure if that counts as a pyramid.
2. I'll bother to answer that if you confirm my answer of 5.
3. Based on a pentagonal base, 108.

I have a feeling I am not understanding the question correctly.

Quote: ChesterDog

Between the three of you, you are...

Correct!!!
----------------------------------------

An old joke...

To get to the other side.

Have you tried 22 tonight? I said 22.

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

October 19th, 2021 at 8:02:41 AM permalink

Freddie the farmer has a paddock that he uses to graze his stock of cows. Each cow eats the same amount of grass each day, regardless of how many other cows are in the paddock and irrespective of the amount of grass left in the paddock. In an experiment, Freddie puts 6 cows into the paddock and he finds out it takes 3 days for them to eat all the grass. These 6 cows are then taken out of the paddock to allow the grass to grow back.

After the grass has been allowed to grow back to the original amount, Freddie then puts 3 cows into the paddock. This time he finds that it takes 7 days for the 3 cows to eat all the grass in the paddock. Freddie is puzzled that the cows took this long and consults a mathematician.

Freddie said "Geez mate, I dunno why me cows took that long to eat me paddock."

Marvin the mathematician replies "Well Freddie, tell me what assumptions you made."

Freddie replies "Well mate, maybe me cows got sick or somethin', cos I reckon that me 3 cows should have taken 6 days to eat me paddock, not 7 days! "

Marvin Replies, "I doubt that very much Freddie!"

After a while Marvin does some calculations and reveals that Freddie had overlooked an important assumption.

Using Marvin's assumption, how long would a single cow take to eat the same paddock?

Have you tried 22 tonight? I said 22.

ThatDonGuy

ThatDonGuy

Threads: 122
Posts: 6739

Joined: Jun 22, 2011

October 19th, 2021 at 8:28:20 AM permalink

Quote: Gialmere

Freddie the farmer has a paddock that he uses to graze his stock of cows. Each cow eats the same amount of grass each day, regardless of how many other cows are in the paddock and irrespective of the amount of grass left in the paddock. In an experiment, Freddie puts 6 cows into the paddock and he finds out it takes 3 days for them to eat all the grass. These 6 cows are then taken out of the paddock to allow the grass to grow back.

After the grass has been allowed to grow back to the original amount, Freddie then puts 3 cows into the paddock. This time he finds that it takes 7 days for the 3 cows to eat all the grass in the paddock. Freddie is puzzled that the cows took this long and consults a mathematician.

Freddie said "Geez mate, I dunno why me cows took that long to eat me paddock."

Marvin the mathematician replies "Well Freddie, tell me what assumptions you made."

Freddie replies "Well mate, maybe me cows got sick or somethin', cos I reckon that me 3 cows should have taken 6 days to eat me paddock, not 7 days! "

Marvin Replies, "I doubt that very much Freddie!"

After a while Marvin does some calculations and reveals that Freddie had overlooked an important assumption.

Using Marvin's assumption, how long would a single cow take to eat the same paddock?
link to original post

The assumption is that the grass keeps growing.

Let x be the fraction of the grass each cow can eat in a day, and y be the fraction of the original grass that grows back in 24 hours.
18x - 2y = 1
21x - 6y = 1
18x - 2y = 21x - 6y
y = 3/4 x
18x - 2y = 1 -> x = 2/33 -> y = 1/22
One cow will eat 4/66 of the field each day, and 3/66 will grow back, so it takes 66 days.

...except that after 62 days of eating and regrowing, 4/66 of the grass remains, all of which is eaten on the 63rd day, so it actually takes 63 days, doesn't it?

Last edited by: ThatDonGuy on Oct 19, 2021

charliepatrick

charliepatrick

Threads: 39
Posts: 3017

Joined: Jun 17, 2011

October 19th, 2021 at 8:44:33 AM permalink

When the farmer puts the cows in the field they immediately feed and then they have their next feed each day, about a day later each time.
In the first case 6 cows feed on Day 0, 1, 2 and 3. So there are, in total, 6x4=24 feeds.
In the second case 3 cows feed on Day 0, 1, 2, 3, 4, 5, 6 and 7. So there are, in total, 3x8=24 feeds.
The error of the farmer was assuming the cows ate at a constant rate, whereas they only eat once a day. In the first case there were 4 feeds for each cow (3 days), in the second, 8 feeds for each cow (7 days). For those not familiar with French, I think that's the logic they use for the word fortnight = "le quinze jours"!

Wizard
Administrator

Threads: 1520
Posts: 27119

Joined: Oct 14, 2009

Thanked by

October 19th, 2021 at 10:04:04 AM permalink

Let:

i = initial amount of grass
g = grass grown in one day
e = grass eaten by one cow in one day

We are given:
i + 3g = 6 * 3 e
i + 7g = 3 * 7 e

In plain English, the first equation says that in 3 days 6 cows eat the initial amount of grass plus what was grown in 3 days.
The second equation says in 7 days 3 cows eat the initial amount of grass plus what was grown in 7 days.

So, we have two equations and three unknowns. That isn't good. However, we don't need to know i to get our answer. Let's assign i an arbitrary value of 100.

Now we have two equations and two unknowns. Some basic matrix algebra results in:

g = 100/21 =~ 4.7619
e = 400/63 =~ 6.3492

Let x = how long it takes one cow to clear the field.

i + xg = xe
x = i/(e-g) = 100/((400/63) - (100/21)) = 63

Putting in other values of i will still result in x = 63.

There is probably a more elegant way to do this, but this is how I did it.

Good problem!

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Wizard
Administrator

Threads: 1520
Posts: 27119

Joined: Oct 14, 2009

October 19th, 2021 at 11:52:57 AM permalink

Farmer Freddy also has sheep. When his sheep graze, they will eat a blade of grass to the ground and then move onto the next blade. They have unlimited space to graze and never return to the same spot they once grazed.

In three days the sheep grazed an acre of grass. Five days after that, they grazed their second acre.

Assume:
1. Sheep consume a constant amount of grass per hour.
2. Grass grows at a constant rate.

How long before the sheep started grazing did the grass grow?

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

October 19th, 2021 at 6:07:17 PM permalink

Quote: Wizard

Let:

i = initial amount of grass
g = grass grown in one day
e = grass eaten by one cow in one day

We are given:
i + 3g = 6 * 3 e
i + 7g = 3 * 7 e

In plain English, the first equation says that in 3 days 6 cows eat the initial amount of grass plus what was grown in 3 days.
The second equation says in 7 days 3 cows eat the initial amount of grass plus what was grown in 7 days.

So, we have two equations and three unknowns. That isn't good. However, we don't need to know i to get our answer. Let's assign i an arbitrary value of 100.

Now we have two equations and two unknowns. Some basic matrix algebra results in:

g = 100/21 =~ 4.7619
e = 400/63 =~ 6.3492

Let x = how long it takes one cow to clear the field.

i + xg = xe
x = i/(e-g) = 100/((400/63) - (100/21)) = 63

Putting in other values of i will still result in x = 63.

There is probably a more elegant way to do this, but this is how I did it.

Good problem!

Correct!!

The data presented is sufficient to calculate both the number of cow-day meals in the field before the cows are introduced and the rate at which the grass grows.

Let M = number of cow-day meals at time zero.
g = amount of grass that grows in one day.

M + 3g = 18 meals : 6 cows 3 days
M + 7g = 21 meals : 3 cows 7 days

M = 63/4 The field starts with 15 3/4 cow-day meals.
g = 3/4 The grass grows at a rate of 3/4 of a cow-day meal per day.

[For one cow in X days, M + Xg = X meals]

If only one cow was let into the field it could eat for 63 days!

-----------------------------------------------------------

Have you tried 22 tonight? I said 22.

ChesterDog

ChesterDog

Threads: 9
Posts: 1730

Joined: Jul 26, 2010

October 20th, 2021 at 9:14:23 AM permalink

Quote: Wizard
Farmer Freddy also has sheep. When his sheep graze, they will eat a blade of grass to the ground and then move onto the next blade. They have unlimited space to graze and never return to the same spot they once grazed.

In three days the sheep grazed an acre of grass. Five days after that, they grazed their second acre.

Assume:
1. Sheep consume a constant amount of grass per hour.
2. Grass grows at a constant rate.

How long before the sheep started grazing did the grass grow?
link to original post

The sheep started grazing 4.5 days after the grass started growing.

Let t stand for the time starting at t = 0 when the sheep first start grazing in that field. And let L be the length of a uneaten grass blade. Then L = a + bt, where a is the length at t = 0, and b is the growth rate of the blade in inches per day.

Call the eating rate of the sheep, expressed as pounds per day, M. It is related to their eating rate expressed as acres per day by:
M = K( a + bt ) dA/dt, where K is some constant related to the number of blades per acre.

Rearranging the equation:
dA = M/[K( a + bt )] dt

Integrating the equation from 0 days to 3 days gives:
1 acre = M/(bK) ln [( a + 3b ) / a]

Integrating from 3 days to 8 days gives:
1 acre = M/(bK) ln [( a + 8b ) / ( a + 3b )]

Equating and dividing both sides by the constants gives:
ln [( a + 3b ) / a] = ln [( a + 8b ) / ( a + 3b )]

Exponentiating both sides to the power e:
( a + 3b ) / a = ( a + 8b ) / ( a + 3b)

Solving:
( a + 3b )² = a² + 8ab
a² + 6ab + 9b² = a² + 8ab
9b² = 2ab
9b = 2a

The length of a grass blade is L = a + bt = a + (2a/9) t.
To achieve the initial length a, the blade would have had to grow 9/2 = 4.5 days.

Wizard
Administrator

Threads: 1520
Posts: 27119

Joined: Oct 14, 2009

Thanked by

October 20th, 2021 at 10:32:07 AM permalink

Quote: ChesterDog

The sheep started grazing 4.5 days after the grass started growing.

Let t stand for the time starting at t = 0 when the sheep first start grazing in that field. And let L be the length of a uneaten grass blade. Then L = a + bt, where a is the length at t = 0, and b is the growth rate of the blade in inches per day.

Call the eating rate of the sheep, expressed as pounds per day, M. It is related to their eating rate expressed as acres per day by:
M = K( a + bt ) dA/dt, where K is some constant related to the number of blades per acre.

Rearranging the equation:
dA = M/[K( a + bt )] dt

Integrating the equation from 0 days to 3 days gives:
1 acre = M/(bK) ln [( a + 3b ) / a]

Integrating from 3 days to 8 days gives:
1 acre = M/(bK) ln [( a + 8b ) / ( a + 3b )]

Equating and dividing both sides by the constants gives:
ln [( a + 3b ) / a] = ln [( a + 8b ) / ( a + 3b )]

Exponentiating both sides to the power e:
( a + 3b ) / a = ( a + 8b ) / ( a + 3b)

Solving:
( a + 3b )² = a² + 8ab
a² + 6ab + 9b² = a² + 8ab
9b² = 2ab
9b = 2a

The length of a grass blade is L = a + bt = a + (2a/9) t.
To achieve the initial length a, the blade would have had to grow 9/2 = 4.5 days.

link to original post

I agree!

I think this one is beer worthy. Thus,

(int)(beers I owe Charlie)++;

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

teliot

Threads: 43
Posts: 2871

Joined: Oct 19, 2009

October 20th, 2021 at 6:28:52 PM permalink

Quote: Wizard
Quote: ChesterDog

The sheep started grazing 4.5 days after the grass started growing.

Let t stand for the time starting at t = 0 when the sheep first start grazing in that field. And let L be the length of a uneaten grass blade. Then L = a + bt, where a is the length at t = 0, and b is the growth rate of the blade in inches per day.

Call the eating rate of the sheep, expressed as pounds per day, M. It is related to their eating rate expressed as acres per day by:
M = K( a + bt ) dA/dt, where K is some constant related to the number of blades per acre.

Rearranging the equation:
dA = M/[K( a + bt )] dt

Integrating the equation from 0 days to 3 days gives:
1 acre = M/(bK) ln [( a + 3b ) / a]

Integrating from 3 days to 8 days gives:
1 acre = M/(bK) ln [( a + 8b ) / ( a + 3b )]

Equating and dividing both sides by the constants gives:
ln [( a + 3b ) / a] = ln [( a + 8b ) / ( a + 3b )]

Exponentiating both sides to the power e:
( a + 3b ) / a = ( a + 8b ) / ( a + 3b)

Solving:
( a + 3b )² = a² + 8ab
a² + 6ab + 9b² = a² + 8ab
9b² = 2ab
9b = 2a

The length of a grass blade is L = a + bt = a + (2a/9) t.
To achieve the initial length a, the blade would have had to grow 9/2 = 4.5 days.

link to original post

I agree!

I think this one is beer worthy. Thus,

(int)(beers I owe Charlie)++;
link to original post

I think you need more parentheses. Maybe I'm getting old.

((int)(beers I owe Charlie))++;

Last edited by: teliot on Oct 20, 2021

Climate Casino: https://climatecasino.net/climate-casino/

Wizard
Administrator

Threads: 1520
Posts: 27119

Joined: Oct 14, 2009

October 20th, 2021 at 6:59:17 PM permalink

Quote: teliot
I think you need more parentheses. Maybe I'm getting old.

((int)(beers I owe Charlie))++;
link to original post

Far be it for me to challenge a computer science teacher, but I think those additional parenthesis are not required. In fact, I think I'll test it...

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Wizard
Administrator

Threads: 1520
Posts: 27119

Joined: Oct 14, 2009

October 20th, 2021 at 7:06:02 PM permalink

Here is my code:


#include <iostream>

int main()
{
	double beers_i_owe_charlie;
	beers_i_owe_charlie = 99;
	printf("Beers owed Charlie before sheep puzzle=\t%f\n", beers_i_owe_charlie);
	(int)(beers_i_owe_charlie)++;
	printf("Beers owed Charlie after sheep puzzle=\t%f\n", beers_i_owe_charlie);	
}

Here is the output:

Quote: output

Beers owed Charlie before sheep puzzle= 99.000000
Beers owed Charlie after sheep puzzle= 100.000000

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Ace2

Ace2

Threads: 32
Posts: 2706

Joined: Oct 2, 2017

October 20th, 2021 at 7:12:11 PM permalink

Nerdiness has just reached a new high

It�s all about making that GTA

teliot

Threads: 43
Posts: 2871

Joined: Oct 19, 2009

October 20th, 2021 at 7:20:05 PM permalink

Quote: Wizard
Here is my code:
#include <iostream>

int main()
{
	double beers_i_owe_charlie;
	beers_i_owe_charlie = 99;
	printf("Beers owed Charlie before sheep puzzle=\t%f\n", beers_i_owe_charlie);
	(int)(beers_i_owe_charlie)++;
	printf("Beers owed Charlie after sheep puzzle=\t%f\n", beers_i_owe_charlie);	
}
Here is the output:

Quote: output

Beers owed Charlie before sheep puzzle= 99.000000
Beers owed Charlie after sheep puzzle= 100.000000

link to original post

if you're only dealing with integer values you don't need (int) at all. I assumed you were dealing with partial beers.

I just looked up using ++ directly on floats and doubles in C. I never thought about this before. It makes for some interesting reading. For example,

https://stackoverflow.com/questions/8561393/is-using-increment-operator-on-floats-bad-style

Climate Casino: https://climatecasino.net/climate-casino/

Wizard
Administrator

Threads: 1520
Posts: 27119

Joined: Oct 14, 2009

October 20th, 2021 at 8:38:11 PM permalink

Quote: teliot
if you're only dealing with integer values you don't need (int) at all.

I agree 100%.

Quote:
I assumed you were dealing with partial beers.

I just looked up using ++ directly on floats and doubles in C. I never thought about this before. It makes for some interesting reading. For example,

https://stackoverflow.com/questions/8561393/is-using-increment-operator-on-floats-bad-style
link to original post

I just read that page and think it vindicates me. It is quite possible that I owed Charlie a non-integer number of beers, as I've been known to give partial credit. Here is some modified code:


#include <iostream>

int main()
{
	double beers_i_owe_charlie;
	beers_i_owe_charlie = 99.5;
	printf("Beers owed Charlie before sheep puzzle=\t%f\n", beers_i_owe_charlie);
	(int)(beers_i_owe_charlie)++;
	printf("Beers owed Charlie after sheep puzzle=\t%f\n", beers_i_owe_charlie);	
}

And the output...

Quote: output

Beers owed Charlie before sheep puzzle= 99.500000
Beers owed Charlie after sheep puzzle= 100.500000

However, I will admit that just tested the same code without the (int) prefix, and the result was the same.

At the time of my initial post, I was not sure what the "++" would do to do decimal, which is why I converted it to an integer.

Nevertheless, I shall go to sleep tonight feeling vindicated. Simple pleasures for simple minds.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Wizard
Administrator

Threads: 1520
Posts: 27119

Joined: Oct 14, 2009

October 20th, 2021 at 8:39:15 PM permalink

Quote: Ace2
Nerdiness has just reached a new high

I wear that as a badge of honor.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

teliot

Threads: 43
Posts: 2871

Joined: Oct 19, 2009

October 20th, 2021 at 9:47:39 PM permalink

Quote: Wizard

At the time of my initial post, I was not sure what the "++" would do to do decimal, which is why I converted it to an integer.

Just to be clear, the ++ is applied before the Integer cast (int), so if your intention was to cast so that ++ was applied to an integer then you didn't get that result.

Mike, there is some serious misunderstanding of coding going on here. The (int) in your code casts the expression as an integer. It does not change the result for the variable beers_i_owe_charlie into that integer. This is unlike the operator ++ that has an actual effect on the variable. To see this --


#include <iostream>

int main()
{
	double beers_i_owe_charlie;
        double x_for_mike;

	beers_i_owe_charlie = 99.5;
	printf("Beers owed Charlie before sheep puzzle=\t%f\n", beers_i_owe_charlie);
	x_for_mike = (int)(beers_i_owe_charlie)++;
	printf("Beers owed Charlie after sheep puzzle=\t%f\n", beers_i_owe_charlie);	
	printf("Mikes owed Charlie after sheep puzzle=\t%f\n", x_for_mike);
}

Quote: output

$ ./a.exe
Beers owed Charlie before sheep puzzle= 99.500000
Beers owed Charlie after sheep puzzle= 100.500000
Mikes owed Charlie after sheep puzzle= 99.000000

BTW, my code was also wrong.

Last edited by: teliot on Oct 21, 2021

Climate Casino: https://climatecasino.net/climate-casino/

Dieter
Administrator

Dieter

Threads: 16
Posts: 6108

Joined: Jul 23, 2014

October 20th, 2021 at 11:46:23 PM permalink

I don't think 6 decimal places of partial beers is what they usually mean by "microbrews".

May the cards fall in your favor.

charliepatrick

charliepatrick

Threads: 39
Posts: 3017

Joined: Jun 17, 2011

October 21st, 2021 at 12:12:38 AM permalink

After all those beers I'll be seeing double integers!

Wizard
Administrator

Threads: 1520
Posts: 27119

Joined: Oct 14, 2009

October 21st, 2021 at 6:21:58 AM permalink

Any objections to:

beers_i_owe_charlie+=1.0; ?

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

teliot

Threads: 43
Posts: 2871

Joined: Oct 19, 2009

October 21st, 2021 at 6:46:19 AM permalink

Quote: Wizard
Any objections to:

beers_i_owe_charlie+=1.0; ?
link to original post

None.

Climate Casino: https://climatecasino.net/climate-casino/

chevy

chevy

Threads: 3
Posts: 151

Joined: Apr 15, 2011

Thanked by

October 21st, 2021 at 7:00:21 AM permalink

Quote: Wizard
Quote: ChesterDog

The sheep started grazing 4.5 days after the grass started growing.

Let t stand for the time starting at t = 0 when the sheep first start grazing in that field. And let L be the length of a uneaten grass blade. Then L = a + bt, where a is the length at t = 0, and b is the growth rate of the blade in inches per day.

Call the eating rate of the sheep, expressed as pounds per day, M. It is related to their eating rate expressed as acres per day by:
M = K( a + bt ) dA/dt, where K is some constant related to the number of blades per acre.

Rearranging the equation:
dA = M/[K( a + bt )] dt

Integrating the equation from 0 days to 3 days gives:
1 acre = M/(bK) ln [( a + 3b ) / a]

Integrating from 3 days to 8 days gives:
1 acre = M/(bK) ln [( a + 8b ) / ( a + 3b )]

Equating and dividing both sides by the constants gives:
ln [( a + 3b ) / a] = ln [( a + 8b ) / ( a + 3b )]

Exponentiating both sides to the power e:
( a + 3b ) / a = ( a + 8b ) / ( a + 3b)

Solving:
( a + 3b )² = a² + 8ab
a² + 6ab + 9b² = a² + 8ab
9b² = 2ab
9b = 2a

The length of a grass blade is L = a + bt = a + (2a/9) t.
To achieve the initial length a, the blade would have had to grow 9/2 = 4.5 days.

link to original post

I agree!

I think this one is beer worthy. Thus,

(int)(beers I owe Charlie)++;
link to original post

Quote: Wizard
Any objections to:

beers_i_owe_charlie+=1.0; ?
link to original post

I am not a lawyer, but as a sometimes Public Offender, I humbly object on behalf of ChesterDog that apart from all this discussion, you seem to be advancing the wrong variable???

beers_i_owe_ChesterDog+=1.0; ?

(NOTE: I don't know "C++" so maybe variable names only go by the first two letters & CHarlie and CHesterDog are the same.)

(NOTE: I am not implying any sock puppetry...too much of that lately)

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

October 21st, 2021 at 8:01:17 AM permalink

Channeling your inner Marty McFly, you travel one week back in time in an attempt to win the lottery. It�s worth $10 million, and each ticket costs a dollar. Note that if you win, your ticket purchase is not refunded. All of this sounds pretty great.

The problem is, you�re not alone. There are 10 other time travelers who also know the winning numbers. You know for a fact that each of them will buy exactly one lottery ticket. Now, according to the lottery�s rules, the prize is evenly split among all the winning tickets (i.e., not evenly among winning people).

How many tickets should you buy to maximize your profits?

Last edited by: Gialmere on Oct 21, 2021

Have you tried 22 tonight? I said 22.

teliot

Threads: 43
Posts: 2871

Joined: Oct 19, 2009

Thanked by

October 21st, 2021 at 8:58:05 AM permalink

Let x be the number of tickets I buy.

Then my win is given by:

win(x) = x*(9999990 - x)/(10+x)

Taking the derivative and setting the numerator to 0 gives a quadratic with positive solution x = 9990 tickets.

Plugging this back in gives a maximized profit of $9,980,010.

My calculus is rusty, so surely I made an error somewhere. I am also not sure if the final prize pool is 9999990-x or 10M - x, based on the problem description.

Last edited by: teliot on Oct 21, 2021

Climate Casino: https://climatecasino.net/climate-casino/

DRich

DRich

Threads: 89
Posts: 12803

Joined: Jul 6, 2012

Thanked by

October 21st, 2021 at 9:47:02 AM permalink

Quote: Dieter
I don't think 6 decimal places of partial beers is what they usually mean by "microbrews".
link to original post

Okay, that was funny and nerdy. My kind of site.

At my age, a "Life In Prison" sentence is not much of a deterrent.

Wizard
Administrator

Threads: 1520
Posts: 27119

Joined: Oct 14, 2009

Thanked by

October 21st, 2021 at 10:21:45 AM permalink

I agree with Eliot's answer. Hopefully I can get some of the credit by showing a more complete solution.

Let n = tickets purchased.
Let f(n) = Net profit = 10,000,000*(n/(n+10)) - n
f'(n) = 10,000,000*((n+10)*1 - n*1)/(n+10)^2 - 1 = 0 (using the quotient rule)
A little cancelling and moving things around gives us:
100,000,000 = (n+10)^2
10,000 = n+10
n = 9,990

I'd like to request that Eliot and I split a beer, on G.

Last edited by: Wizard on Mar 21, 2022

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

teliot

Threads: 43
Posts: 2871

Joined: Oct 19, 2009

October 21st, 2021 at 10:26:38 AM permalink

Quote: Wizard

I agree with Eliot's answer. Hopefully I can get some of the credit by showing a more complete solution.

Let n = tickets purchased.
Let f(n) = Net profit = 10,000,000*(n/(n+10)) - n
f'(n) = 10,000,000*((n+10)*1 - n*1)/(n+10)^2 - 1 = 0 (using the quotient rule)
A little cancelling and moving things around gives us:
10,000,000 = (n+10)^2
10,000 = n+10
n = 9,990

I'd like to request that Eliot and I split a beer, on G.

link to original post

Mike, I would request that my 1/2 beer be donated to The Animal Foundation -- https://animalfoundation.com/

Climate Casino: https://climatecasino.net/climate-casino/

Wizard
Administrator

Threads: 1520
Posts: 27119

Joined: Oct 14, 2009

October 21st, 2021 at 1:58:33 PM permalink

This problem is inspired by the Squid Game, which I highly recommend to anybody not squeamish about blood. Mrs. Wizard couldn't take it and had to leave the room.

In one of the games there is a glass bridge. The bridge is divided into glass panels in an 18 by 2 grid. Let's explain it as 18 rows and two columns. In each row, one piece of glass is tempered, meaning a player could easily stand in it without the glass breaking. The other piece was ordinary glass that would break under the weight of a player.

The players must advance, one at a time, in a predesignated order. There are 16 total players. The rules are a little different on the show, but let's keep it simple here.

Assuming random guessing at each new row, what is the expected number of players to cross safely?

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

unJon

unJon

Threads: 16
Posts: 4808

Joined: Jul 1, 2018

October 21st, 2021 at 2:02:01 PM permalink

How many players?

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

Wizard
Administrator

Threads: 1520
Posts: 27119

Joined: Oct 14, 2009

October 21st, 2021 at 2:04:09 PM permalink

Quote: unJon
How many players?
link to original post

Sorry, I forgot that. I amended the question to say there are 16 players and 18 rows.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Ace2

Ace2

Threads: 32
Posts: 2706

Joined: Oct 2, 2017

October 21st, 2021 at 5:11:24 PM permalink

Just off the top of my head: it should take each player an average of two steps to reach weak glass. Therefore it should take nine players to advance eighteen rows and the remaining seven will all cross successfully

It�s all about making that GTA

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

Thanked by

October 21st, 2021 at 5:41:58 PM permalink

Quote: teliot
Let x be the number of tickets I buy.

Then my win is given by:

win(x) = x*(9999990 - x)/(10+x)

Taking the derivative and setting the numerator to 0 gives a quadratic with positive solution x = 9990 tickets.

Plugging this back in gives a maximized profit of $9,980,010.

My calculus is rusty, so surely I made an error somewhere. I am also not sure if the final prize pool is 9999990-x or 10M - x, based on the problem description.

link to original post

Quote: Wizard

I agree with Eliot's answer. Hopefully I can get some of the credit by showing a more complete solution.

Let n = tickets purchased.
Let f(n) = Net profit = 10,000,000*(n/(n+10)) - n
f'(n) = 10,000,000*((n+10)*1 - n*1)/(n+10)^2 - 1 = 0 (using the quotient rule)
A little cancelling and moving things around gives us:
10,000,000 = (n+10)^2
10,000 = n+10
n = 9,990

I'd like to request that Eliot and I split a beer, on G.

link to original post

Correct!!!

Although I think the organizers might get suspicious with so many winning tickets.
---------------------------------------------------

I was going to tell a Time Travel joke...

...but you guys didn't like it.

Have you tried 22 tonight? I said 22.

aceside

aceside

Threads: 2
Posts: 591

Joined: May 14, 2021

October 21st, 2021 at 6:26:41 PM permalink

Quote: Ace2
Just off the top of my head: it should take each player an average of two steps to reach weak glass. Therefore it should take nine players to advance eighteen rows and the remaining seven will all cross successfully

link to original post

Let me offer a slightly different solution.

It should take each player an average of 3 steps to reach weak glass. Therefore it should take 6 players to advance 18 rows and the remaining 10 players will all cross successfully.

Wizard
Administrator

Threads: 1520
Posts: 27119

Joined: Oct 14, 2009

October 21st, 2021 at 9:31:11 PM permalink

I'm still looking for a correct answer.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

HopHoofer

HopHoofer

Threads: 1
Posts: 18

Joined: Oct 13, 2021

October 21st, 2021 at 11:29:29 PM permalink

Quote: Wizard

x = sqrt(5*sqrt(5*sqrt(5*sqrt(5*sqrt(5*sqrt(5*sqrt(5*sqrt(5*sqrt(5*sqrt(5*sqrt(5*sqrt(5*sqrt(....))))))))))))))))

What is x?
link to original post

x^2 = 5 * x
so x = 5

Last edited by: HopHoofer on Oct 21, 2021

HopHoofer

HopHoofer

Threads: 1
Posts: 18

Joined: Oct 13, 2021

October 21st, 2021 at 11:48:38 PM permalink

Quote: Wizard
Here is your next puzzle that is too simple to be beer-worthy, but is nevertheless pretty challenging.

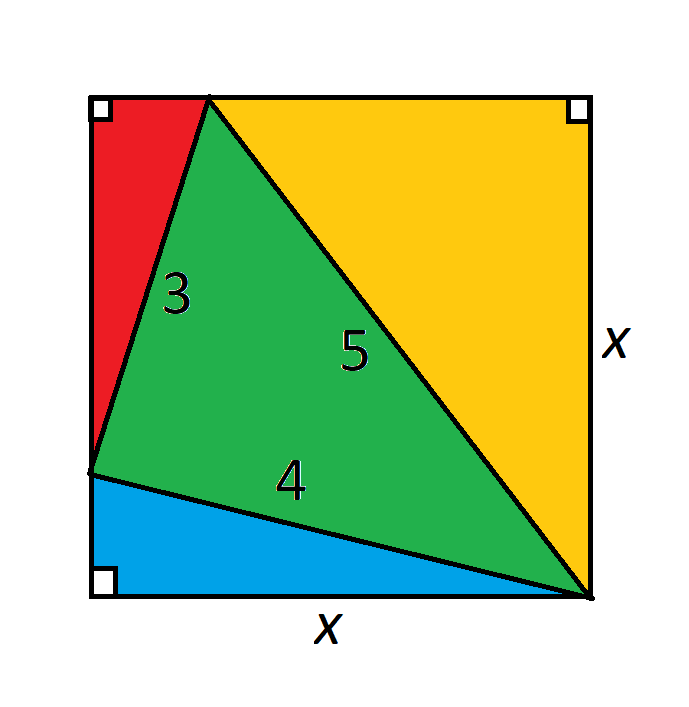
A 3-4-5 triangle is inscribed in a square of length x.

Find x.
link to original post

(x-sqrt(25-x^2))^2 + (x-sqrt(16-x^2))^2 = 9
==> x Sqrt[25 - x^2] + x Sqrt[16 - x^2] = 16

2 possible lengths: 16/sqrt(17) and 16/sqrt(65)

HopHoofer

HopHoofer

Threads: 1
Posts: 18

Joined: Oct 13, 2021

October 22nd, 2021 at 12:51:42 AM permalink

Quote: Wizard
I'm still looking for a correct answer.
link to original post

My result is 7.00008.

Here is my solution. If a player can stand on a row, then mark the row as 1, otherwise mark the row as 0. Consider the binary representation of 18 rows as a bit map, if there are 4 0s, for example, it means, 12 players can finally make it.

So the result is [C(18, 0) * 16 + C(18, 1) * 15 + ... + C(18, 15) * 1 + C(18, 16) * 0] / (2^18) = 458757/65536 ~=7

Last edited by: HopHoofer on Oct 22, 2021

ThatDonGuy

ThatDonGuy

Threads: 122
Posts: 6739

Joined: Jun 22, 2011

October 22nd, 2021 at 7:43:32 AM permalink

Quote: HopHoofer
Quote: Wizard
I'm still looking for a correct answer.
link to original post

My result is 7.00008.

Here is my solution. If a player can stand on a row, then mark the row as 1, otherwise mark the row as 0. Consider the binary representation of 18 rows as a bit map, if there are 4 0s, for example, it means, 12 players can finally make it.

So the result is [C(18, 0) * 16 + C(18, 1) * 15 + ... + C(18, 15) * 1 + C(18, 16) * 0] / (2^18) = 458757/65536 ~=7

link to original post

I got the same solution, in the same way, but described slightly differently:

When a row is reached for the first time, it will be crossed successfully with probability 1/2 and unsuccessfully with probability 1/2. Every subsequent contestant will cross that row successfully. Therefore, the number of survivors = 16 - the number that chose incorrectly.
There is 1 way to choose zero rows incorrectly, resulting in 16 successful crossings.
There are C(18,1) = 18 ways to choose one row incorrectly, resulting in 15 successful crossings.
There are C(18,2) = 153 ways to choose two rows incorrectly, resulting in 14 successful crossings.
...
There are C(18,15) = 816 ways to choose 15 rows incorrectly, resulting in one successful crossing.
All remaining ways will result in zero crossings.
Each way has probability (1/2)^18 = 1 / 2^18 of occuring, so the probability = (1 x 16 + C(18,1) x 15 + C(18,2) x 14 + ... + C(18,15) x 1) / 2^18 = 458757 / 65536 = 7 + 5 / 65536.

Ace2

Ace2

Threads: 32
Posts: 2706

Joined: Oct 2, 2017

October 22nd, 2021 at 12:42:29 PM permalink

If there were 18 or more players then my method would work. So if, for instance, there were 24 players, then an average of 24 - 18/2 = 15 players would cross.

But since there are only 16 players, you must add back the impossible cases where 17 and 18 players fail. So:

16 - 18/2 + (c(18,17)*1 + c(18,18)*2) / 2^18 =~ 7.00008

I was scratching my head�didn�t understand why my method was very close but incorrect

It�s all about making that GTA

Wizard
Administrator