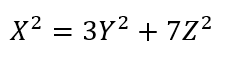Easy math puzzles

Quote: Wizard

On a windless day, Charlie takes his canoe to the river and paddles up upstream. He always paddles at the same rate (in other words if we ignore the current, he would always go the same speed). A mile* after launching, his hat falls in the river. Ten minutes after that, he realizes his hat is missing and immediately makes a u-turn to catch up to it downstream. Charlie catches up to his hat at the same place he launched.

How fast is the current?



Note: I originally, incorrectly, said "an hour." It should be a mile.
link to original post

Quote: teliot

I saw this problem on Twitter -- it has a rather easy argument.

Find all solutions X, Y, Z in integers to:


link to original post

Quote: aceside

My solution:

Show Spoiler

Set current speed=x; set boat speed=v; set time used by boat in the return trip=t, then we get two equations:
1+10(v-x)=(v+x)t,
(t+10)x=1.
Solve this set of two equations, we find the current speed x=0.05 mile/minute.

link to original post

Quote: aceside

Quote: teliot

I saw this problem on Twitter -- it has a rather easy argument.

Find all solutions X, Y, Z in integers to:


link to original post

I could not find a solution when z<=25.

Quote: Wizard

I apologize if discussion of the semi-sphere problem isn't finished. I also apologize if I asked this one before. I do know I asked a similar one.

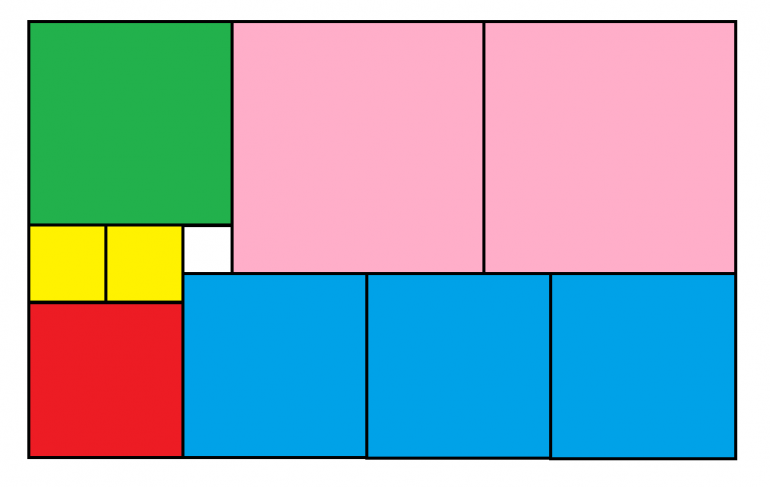
Consider the following figure. All pieces are squares. The area of the white square is 25. What is the area of the entire figure?


link to original post

Quote: teliot

I saw this problem on Twitter -- it has a rather easy argument.

Find all solutions X, Y, Z in integers to:


link to original post

Quote: teliot

I saw this problem on Twitter -- it has a rather easy argument.

Find all solutions X, Y, Z in integers to:


link to original post

Quote: GM

Quote: Wizard

I apologize if discussion of the semi-sphere problem isn't finished. I also apologize if I asked this one before. I do know I asked a similar one.

Consider the following figure. All pieces are squares. The area of the white square is 25. What is the area of the entire figure?


link to original post

An aside, not related to the solution of this particular problem: There is a lot of interesting mathematics related to dividing rectangles (including squares) into squares, it has an unexpected connection to graph theory and electric circuits. It is possible to divide a square into smaller squares of different sizes, but it is definitely not an easy mathematical problem. www.squaring.net is a website dedicated to this type of problems, the history and theory section has a number of interesting articles about the development of the problem, the articles about Brooks, Smith, Stone and Tutte are particularly interesting.
link to original post

Quote: teliot

I saw this problem on Twitter -- it has a rather easy argument.... Find all solutions X, Y, Z in integers to: ...

link to original post

Quote: gordonm888

Quote: teliot

I saw this problem on Twitter -- it has a rather easy argument.

Find all solutions X, Y, Z in integers to:


link to original post

This problem statement suffers from the lack of a bikini-clad blonde in a rubber boat.

Show Spoiler

Any integer X = S *(Y^2 + Z^2) only has solutions when Y^2 +Z^2 is either
- a pythagoran prime (2 or any 1mod4 prime)
- or any possible product of pythagoran primes.
- or any of the above two possibilities when both multiplied by a common squared integer (in which case we can factor out that common squared integer and redefine it as part of S.)

For X^2 = 3Y^2 + 7Z^2, the first question is whether (3Y^2 + 7z^2) can ever be a 1mod4 prime or a product of 1mod4 primes. I think the answer is no, there are no solutions when Y,Z are non-zero integers.

There are also no solutions when Y=0 or when Z = 0; because X^2 = 3Y^2 and X^2= 7Z^2 have no solutions.

What about when X = 0? No solutions, because the square of any negative or positive integer >0.

Thus, the only solution I see is X=Y=Z=0.

link to original post

Quote: GM

Quote: teliot

I saw this problem on Twitter -- it has a rather easy argument.

Find all solutions X, Y, Z in integers to:


link to original post

Show Spoiler

The only solution is X=Y=Z=0. Let's assume that there exists another integer solution. Let's choose a solution X, Y, Z with |X| minimal among the solutions which are not all 0. (X clearly cannot be 0.)

The square of any even number is divisible by 4, while the square of any odd number has remainder 1 on division by 4.
If Y and Z are both odd, then the remainder of the right-hand side on division by 4 is 2, so it cannot be a square.
If one of Y and Z is odd and the other is even, then remainder of the right-hand side on division by 4 is 3, so it cannot be a square either.
If both Y and Z are even, then the right-hand side is divisible by 4, so X also has to be even. X/2, Y/2, Z/2 are all integers, not all 0, (X/2)^2=3(Y/2)^2+7(Z/2)^2 and |X/2|<|X|, contradicting the minimality of |X|, therefore there is no solution other than X=Y=Z=0.

Looking at remainders on division by 7 also works.

link to original post

Quote: charliepatrick

Quote: teliot

I saw this problem on Twitter -- it has a rather easy argument.... Find all solutions X, Y, Z in integers to: ...

link to original post

I was using similar logic but using 3s and 7s

For all N: N² is 0 or 1 mod 3 (consider all numbers are either 3n, 3n+1 or 3n-1)
For all N: N² is 0, 1, 2 or 4 mod 7 (similarly consider 7n 7n+1 7n+2 7n+3 7n-3 7n-2 7n-1)
For all X: X² is 0, 1, 4, 7, 9, 15, 16 or 18 mod 21
For all Y: 3*Y² is 0, 3, 6 or 12 mod 21
For all Z: 7*Z² is 0 or 7 mod 21
Also if N² is divisible by 7 then so is N.
Since X² (mod 21) = 3*Y² (mod 21) + 7*Z² (mod 21), the only combinations that work are (0,0,0) and (7,7,0)
Thus X² is either 0 or 7 mod 21, ie X is divisible by 7.
Since 7*Z² is divisible by 7 it follows 3*Y² has to be divisible by 7 as well.
So X and Y have to be divisible by 7.

So X² and Y² are divisible by 49, this means Z² is divisible by 7 meaning Z has to be as well.

This leads to the conclusion that if (X,Y,Z) is a solution then (X/7,Y/7,Z/7) must be, this can't be true for any X>0, so means the only solution is (0,0,0).

link to original post

Quote: teliot

Quote: charliepatrick

Quote: teliot

I saw this problem on Twitter -- it has a rather easy argument.... Find all solutions X, Y, Z in integers to: ...

link to original post

I was using similar logic but using 3s and 7s

For all N: N² is 0 or 1 mod 3 (consider all numbers are either 3n, 3n+1 or 3n-1)
For all N: N² is 0, 1, 2 or 4 mod 7 (similarly consider 7n 7n+1 7n+2 7n+3 7n-3 7n-2 7n-1)
For all X: X² is 0, 1, 4, 7, 9, 15, 16 or 18 mod 21
For all Y: 3*Y² is 0, 3, 6 or 12 mod 21
For all Z: 7*Z² is 0 or 7 mod 21
Also if N² is divisible by 7 then so is N.
Since X² (mod 21) = 3*Y² (mod 21) + 7*Z² (mod 21), the only combinations that work are (0,0,0) and (7,7,0)
Thus X² is either 0 or 7 mod 21, ie X is divisible by 7.
Since 7*Z² is divisible by 7 it follows 3*Y² has to be divisible by 7 as well.
So X and Y have to be divisible by 7.

So X² and Y² are divisible by 49, this means Z² is divisible by 7 meaning Z has to be as well.

This leads to the conclusion that if (X,Y,Z) is a solution then (X/7,Y/7,Z/7) must be, this can't be true for any X>0, so means the only solution is (0,0,0).

link to original post

A nice alternative solution, full points!
link to original post

Quote: aceside

Quote: teliot

Quote: charliepatrick

Quote: teliot

I saw this problem on Twitter -- it has a rather easy argument.... Find all solutions X, Y, Z in integers to: ...

link to original post

I was using similar logic but using 3s and 7s

For all N: N² is 0 or 1 mod 3 (consider all numbers are either 3n, 3n+1 or 3n-1)
For all N: N² is 0, 1, 2 or 4 mod 7 (similarly consider 7n 7n+1 7n+2 7n+3 7n-3 7n-2 7n-1)
For all X: X² is 0, 1, 4, 7, 9, 15, 16 or 18 mod 21
For all Y: 3*Y² is 0, 3, 6 or 12 mod 21
For all Z: 7*Z² is 0 or 7 mod 21
Also if N² is divisible by 7 then so is N.
Since X² (mod 21) = 3*Y² (mod 21) + 7*Z² (mod 21), the only combinations that work are (0,0,0) and (7,7,0)
Thus X² is either 0 or 7 mod 21, ie X is divisible by 7.
Since 7*Z² is divisible by 7 it follows 3*Y² has to be divisible by 7 as well.
So X and Y have to be divisible by 7.

So X² and Y² are divisible by 49, this means Z² is divisible by 7 meaning Z has to be as well.

This leads to the conclusion that if (X,Y,Z) is a solution then (X/7,Y/7,Z/7) must be, this can't be true for any X>0, so means the only solution is (0,0,0).

link to original post

A nice alternative solution, full points!
link to original post

Here is my proof of this problem using parametric equations

Show Spoiler

The equation (represents an elliptical cone) can be parametrized into a set of three equations:
X=r,
Y=r cos(t)/Sqrt(3),
Z=r sin(t)/Sqrt(7).
If X=r is a positive integer, Y and Z cannot be both integers simultaneously, because of their correlation.
This proof can be generalized to any quadratic equations with different coefficients.

link to original post

Quote: aceside

I am thinking in 2D. To have a non-zero integer solution, we must have tan(t)=sin(t)/cos(t)=m/n, as a fraction. In this problem, tan(t)=(m/n)Sqrt(7/3), is not a fraction; therefore, there is no solution.
link to original post

Quote: GM

Quote: aceside

I am thinking in 2D. To have a non-zero integer solution, we must have tan(t)=sin(t)/cos(t)=m/n, as a fraction. In this problem, tan(t)=(m/n)Sqrt(7/3), is not a fraction; therefore, there is no solution.
link to original post

If this type of argument worked, it would also work if you changed the coefficient 3 to 2 in the equation. However, X^2=2Y^2+7Z^2 has non-trivial solutions, for example, X=3, Y=1, Z=1.
link to original post

Quote: aceside

Quote: GM

Quote: aceside

I am thinking in 2D. To have a non-zero integer solution, we must have tan(t)=sin(t)/cos(t)=m/n, as a fraction. In this problem, tan(t)=(m/n)Sqrt(7/3), is not a fraction; therefore, there is no solution.
link to original post

If this type of argument worked, it would also work if you changed the coefficient 3 to 2 in the equation. However, X^2=2Y^2+7Z^2 has non-trivial solutions, for example, X=3, Y=1, Z=1.
link to original post

Interesting! For a general quadric surface equation x^2=a*y^2+b*z^2, what integer coefficients a and b can make non-zero integer solutions happen?
link to original post

Quote: Wizard

What is the area of a regular pentagon of side length 1?

Quote: Wizard

Pretty good, Don! Next can you express the answer without trig functions?
link to original post

Tip for Don

Triangles ABC and ADC are similar.

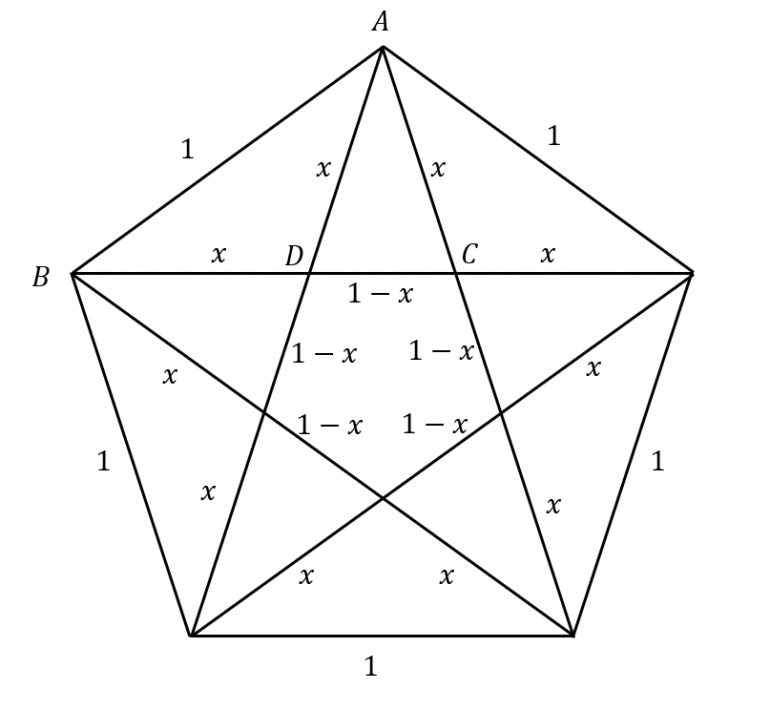
Quote: Wizard

Pretty good, Don! Next can you express the answer without trig functions?
link to original post

Quote: ThatDonGuy

Thanks to ChesterDog's hint...

Using the image in ChesterDog's hint:

x / (1 - x) = 1 / x
x^2 = 1 - x
x^2 + x - 1 = 0
x = -1/2 + sqrt(5)/2
x^2 = (3 - sqrt(5)) / 2
tan 54 = (1/2) / sqrt(x^2 - 1/4) = 1 / (2 sqrt(x^2 - 1/4)) = 1 / sqrt(5 - 2 sqrt(5))

Area = 5 / (4 sqrt(5 - 2 sqrt(5)))
= 5 sqrt(5 - 2 sqrt(5)) / (20 - 8 sqrt(5))
= (100 + 40 sqrt(5)) sqrt(5 - 2 sqrt(5)) / 80
= (5 + 2 sqrt(5)) sqrt(5 - 2 sqrt(5)) / 4

link to original post

Quote: Wizard

Quote: ThatDonGuy

Thanks to ChesterDog's hint...

Area = (5 + 2 sqrt(5)) sqrt(5 - 2 sqrt(5)) / 4

link to original post

I agree! I express the answer as...

Show Spoiler

(sqrt(5)/4)*sqrt(5+2*sqrt(5)) = apx. 1.7205

link to original post

Quote: Wizard

I think a better way to express the answer is...

Show Spoiler

sqrt(5*(5+2*sqrt(5))/4

link to original post

Quote: Gialmere

From Riddler 538 comes this pair of football puzzles...



Problem #2
Hames Jarrison has just intercepted a pass at one end zone of a football field, and begins running — at a constant speed of 15 miles per hour — to the other end zone, 100 yards away.

At the moment he catches the ball, you are on the very same goal line, but on the other end of the field, 50 yards away from Jarrison. Caught up in the moment, you decide you will always run directly toward Jarrison’s current position, rather than plan ahead to meet him downfield along a more strategic course.

Assuming you run at a constant speed (i.e., don’t worry about any transient acceleration), how fast must you be in order to catch Jarrison before he scores a touchdown?
link to original post

Quote: Gialmere

From Riddler 538 comes this pair of football puzzles...



Problem #2
Hames Jarrison has just intercepted a pass at one end zone of a football field, and begins running — at a constant speed of 15 miles per hour — to the other end zone, 100 yards away.

At the moment he catches the ball, you are on the very same goal line, but on the other end of the field, 50 yards away from Jarrison. Caught up in the moment, you decide you will always run directly toward Jarrison’s current position, rather than plan ahead to meet him downfield along a more strategic course.

Assuming you run at a constant speed (i.e., don’t worry about any transient acceleration), how fast must you be in order to catch Jarrison before he scores a touchdown?

link to original post

Quote: teliot

Find all values of N such that N! + (N+1)! + (N+2)! is a perfect square.
link to original post

Quote: ThatDonGuy

Quote: teliot

Find all values of N such that N! + (N+1)! + (N+2)! is a perfect square.
link to original post

Answer...sort of

N! + (N + 1)! + (N + 2)! = N! (1 + (N + 1) + (N + 1)(N + 2)) = N! (N + 2)^2
Therefore, the sum is a perfect square if and only if N! is a perfect square.

As far as I know, the only factorials that are perfect squares are 0! and 1!, so N = 0 and N = 1 are the only solutions.
I am not sure that all factorials > 1! are not squares has been proven; it depends on something called Bertrand's postulate (for all integers N >= 2, there is at least one prime number greater than N and less than 2N).

link to original post

Quote: teliot

Show that if p and p^2 + 8 are both primes, then p^3 + 4 is also a prime.
link to original post

Quote: charliepatrick

Quote: teliot

Show that if p and p^2 + 8 are both primes, then p^3 + 4 is also a prime.
link to original post

Show Spoiler

Obviously it doesn't work for 2 (2, 12) or 5 (5 33), 7 (7 57), but does work for 3 (3 17 31).
What is interesting is any prime greater than 3 is of the form (3n+1) or (3n-1), so p²+8 will be (3n+/-1)*(3n+/-1)+8 = 9n²+/-6n+1+8, or 3xsomething+9, which is divisible by 3.
Hence only p=3 satisfies the first part. So the statement is true as the only value can be p=3.

link to original post

Quote: teliot

Show that if p and p^2 + 8 are both primes, then p^3 + 4 is also a prime.
link to original post

Quote: teliot

Quote: ThatDonGuy

Quote: teliot

Find all values of N such that N! + (N+1)! + (N+2)! is a perfect square.
link to original post

Answer...sort of

N! + (N + 1)! + (N + 2)! = N! (1 + (N + 1) + (N + 1)(N + 2)) = N! (N + 2)^2
Therefore, the sum is a perfect square if and only if N! is a perfect square.

As far as I know, the only factorials that are perfect squares are 0! and 1!, so N = 0 and N = 1 are the only solutions.
I am not sure that all factorials > 1! are not squares has been proven; it depends on something called Bertrand's postulate (for all integers N >= 2, there is at least one prime number greater than N and less than 2N).

link to original post

Bertrands postulate is true. I actually presented the proof to one of my classes back in 1984. But yes, you can use that result and get the answer. I wonder if you don't need to though. You know, use an atom bomb to smash an ant.
link to original post

Quote: gordonm888

Quote: teliot

Show that if p and p^2 + 8 are both primes, then p^3 + 4 is also a prime.
link to original post

Hoping to get more than a 0 for this answer

All primes >5 are congruent with 1or5mod(6), also written as ∓1mod(6). This is basically equivalent to saying that primes are not divisible by 2 or 3.

If a prime p is congruent with +1mod(6), then p³ must be congruent with +3mod(6) and p³+4 is of the form +1mod(6) and thus is not forbidden to be a prime. Similarly if p is congruent with -1mod(6), then p³+4 is congruent with +1mod(6) and may possibly be prime.

But, the problem statement requires that both p and p²+8 must be prime. Since p is congruent with ∓1mod(6) then p² must be congruent with either ∓2mod(6) and p²+8 must be congruent with either 0mod(6) or 4mod 6. Thus , the only way that p²+8 can be prime is if p is 5 or less. Testing p=2,3,5, it appears that p=3 is the only solution for the initial conditions.

So given that p=3 is the only possible value of p, I note that p³+4 =27 +4=31, which is indeed prime.

link to original post

Quote: gordonm888

Quote: gordonm888

Quote: teliot

Show that if p and p^2 + 8 are both primes, then p^3 + 4 is also a prime.
link to original post

Hoping to get more than a 0 for this answer

All primes >5 are congruent with 1or5mod(6), also written as ∓1mod(6). This is basically equivalent to saying that primes are not divisible by 2 or 3.

If a prime p is congruent with +1mod(6), then p³ must be congruent with +3mod(6) and p³+4 is of the form +1mod(6) and thus is not forbidden to be a prime. Similarly if p is congruent with -1mod(6), then p³+4 is congruent with +1mod(6) and may possibly be prime.

But, the problem statement requires that both p and p²+8 must be prime. Since p is congruent with ∓1mod(6) then p² must be congruent with either ∓2mod(6) and p²+8 must be congruent with either 0mod(6) or 4mod 6. Thus , the only way that p²+8 can be prime is if p is 5 or less. Testing p=2,3,5, it appears that p=3 is the only solution for the initial conditions.

So given that p=3 is the only possible value of p, I note that p³+4 =27 +4=31, which is indeed prime.

link to original post

link to original post

Quote: ThatDonGuy

Quote: teliot

Quote: ThatDonGuy

Quote: teliot

Find all values of N such that N! + (N+1)! + (N+2)! is a perfect square.
link to original post

Answer...sort of

N! + (N + 1)! + (N + 2)! = N! (1 + (N + 1) + (N + 1)(N + 2)) = N! (N + 2)^2
Therefore, the sum is a perfect square if and only if N! is a perfect square.

As far as I know, the only factorials that are perfect squares are 0! and 1!, so N = 0 and N = 1 are the only solutions.
I am not sure that all factorials > 1! are not squares has been proven; it depends on something called Bertrand's postulate (for all integers N >= 2, there is at least one prime number greater than N and less than 2N).

link to original post

Bertrands postulate is true. I actually presented the proof to one of my classes back in 1984. But yes, you can use that result and get the answer. I wonder if you don't need to though. You know, use an atom bomb to smash an ant.
link to original post

In case anyone is still trying to figure this out

Your use of, "I wonder if you don't need to though," leads me to believe that you don't have a solution, or at least one that doesn't depend on Bertrand's Postulate.

Let P be the largest prime number <= N. By the Fundamental Theorem of Arithmetic, if N! is a square, then P must appear an even number of times in N!'s prime factorization. This means that 2P <= N, as otherwise P will appear only once. Since P being the largest prime number <= N is given, this means that there are no primes from P+1 to 2P inclusive, which contradicts Bertrand's Postulate.

Quote: teliot

Quote: gordonm888

Quote: gordonm888

Quote: teliot

Show that if p and p^2 + 8 are both primes, then p^3 + 4 is also a prime.
link to original post

Hoping to get more than a 0 for this answer

All primes >5 are congruent with 1or5mod(6), also written as ∓1mod(6). This is basically equivalent to saying that primes are not divisible by 2 or 3.

If a prime p is congruent with +1mod(6), then p³ must be congruent with +3mod(6) and p³+4 is of the form +1mod(6) and thus is not forbidden to be a prime. Similarly if p is congruent with -1mod(6), then p³+4 is congruent with +1mod(6) and may possibly be prime.

But, the problem statement requires that both p and p²+8 must be prime. Since p is congruent with ∓1mod(6) then p² must be congruent with either ∓2mod(6) and p²+8 must be congruent with either 0mod(6) or 4mod 6. Thus , the only way that p²+8 can be prime is if p is 5 or less. Testing p=2,3,5, it appears that p=3 is the only solution for the initial conditions.

So given that p=3 is the only possible value of p, I note that p³+4 =27 +4=31, which is indeed prime.

link to original post

link to original post

Your claim that if p is congruent to 1 mod 6 then p³ must be congruent with +3mod(6) is false. For example, p = 7, then p is congruent to 1 mod 6. Note that 7^3 = 343 is also congruent to 1 mod 6.

Your claim that if p is congruent to 1 mod 6 then p² must be congruent with either ∓2mod(6) is also false. Again, p = 7, then 7^2 = 49 is congruent to 1 mod 6. Note that integers of the form ∓2mod(6) are always even, whereas any power of p is odd, so such a congruence could never be possible.

In general, if p is congruent to 1 mod 6 then all power of p will also be congruent to 1 mod 6.

You get a point for effort and another point for the correct answer (without a valid argument why it's correct), but that's all the points you get on this.
link to original post

Quote: teliot

For any integer N, consider the list of all primes that are in the half-open interval (N/2,N]. Call them p1, p2, p3 ... , pk. The question is, for which N is N!/(p1*p2*p3*...*pk) a perfect square? In other words, divide N! by all the primes greater than N/2 and less than or equal to N (the Bertrand's Postulate primes) and ask if what's leftover is a perfect square.

Any others? Infinitely many? This isn't in the OEIS (at least that I can find).
link to original post

Quote: Gialmere

Still in play...

Quote: Gialmere

From Riddler 538 comes this pair of football puzzles...



Problem #2
Hames Jarrison has just intercepted a pass at one end zone of a football field, and begins running — at a constant speed of 15 miles per hour — to the other end zone, 100 yards away.

At the moment he catches the ball, you are on the very same goal line, but on the other end of the field, 50 yards away from Jarrison. Caught up in the moment, you decide you will always run directly toward Jarrison’s current position, rather than plan ahead to meet him downfield along a more strategic course.

Assuming you run at a constant speed (i.e., don’t worry about any transient acceleration), how fast must you be in order to catch Jarrison before he scores a touchdown?
link to original post

link to original post

Quote: charliepatrick

Quote: Gialmere

......Which draft position should you choose to maximize your expected fantasy score?...

Show Spoiler

Pick B.

A's best strategy is to pick QB400. B has a choice of QB350 or RB300.
(i) In the former C is now guaranteed QB300 so picks RB300 and WR250, B will choose WR225 over RB225. A=800, B=775, C=850.
(ii) In the latter C chooses QB350 and RB250, B then chooses WR225 and will eventually get QB300. A=800, B=825, C=800.

So by choosing B and RB300 you get 825.

link to original post

Quote: ChesterDog

Quote: Gialmere

Still in play...

Quote: Gialmere

From Riddler 538 comes this pair of football puzzles...



Problem #2
Hames Jarrison has just intercepted a pass at one end zone of a football field, and begins running — at a constant speed of 15 miles per hour — to the other end zone, 100 yards away.

At the moment he catches the ball, you are on the very same goal line, but on the other end of the field, 50 yards away from Jarrison. Caught up in the moment, you decide you will always run directly toward Jarrison’s current position, rather than plan ahead to meet him downfield along a more strategic course.

Assuming you run at a constant speed (i.e., don’t worry about any transient acceleration), how fast must you be in order to catch Jarrison before he scores a touchdown?
link to original post

link to original post

Show Spoiler

Since it's an easy math problem, I used an easy method of numerical approximation. I started at (0, 50) and Jarrison started at (0, 0). Starting at t = 0 seconds, I ran toward (0,0). Starting at t = 0.0025 seconds, I ran toward the position reached by Jarrison at t = 0.0025 seconds, which was (0.1833, 0), and so on until Jarrison and I reached (100, 0) simultaneously.

This method gave me an answer of about 19.21 miles per hour.

link to original post

Official Solves

Problem #1
Here’s what Riddler Nation had to say:

19.9 percent of readers said they would draft first.
62.3 percent of readers said they would draft second.
17.7 percent of readers said they would draft third.

The majority opted to draft second. But was that the best strategy?

At first glance, some readers thought Osh Jallen (350 points) was a better pick than Caffrey McChristian (300 points). However, missing out on Jallen meant you could grab Myler Kurray, who was only 50 points lower. Meanwhile, missing out on McChristian meant that your running back, at best, was 75 points lower. So while Jallen had more expected points, McChristian was the more valuable pick in the draft.

To better make sense of this, it was helpful to rescale all the expected point values, as solver Johnny of Toronto, Canada, did. All that mattered were the relative differences between the scores. One way to rescale them was to say that the lowest-scoring player at each position was worth 0 points, and that every 25 “original” points were worth 1 “rescaled” point. That meant the quarterbacks (QBs) were respectively worth 4, 2 and 0 points; the running backs (RBs) were worth 4, 1 and 0 points; and the wide receivers (WRs) were worth 3, 2 and 0 points.

Person A’s best move was to grab one of the 4-pointers — either the top QB or the top RB. Suppose they picked the top QB, which meant B picked the top RB, giving them 4 points apiece. From there, C would pick the top WR for 3 points as well as the second QB for 2 points, netting them 5 points in total (since the third picks were all worth 0 points). Because of the snake draft ordering, B got the next pick. They would have snagged the top remaining player, which was the second WR for another 2 points. Finally, A would have drafted the second RB for 1 point. During the final round, each person would have drafted the position they needed to complete their roster. For this scenario, the final result was: 5 points for A, 6 points for B and 5 points for C.

Drafting second was looking good so far. But what if person A had opted for the other 4-pointer, the top RB?

In this case, B would have taken the top QB. The picks for C would have remained the same: the top WR and the second QB, for a total of 5 points. Once again, B then picked the second WR. At this point, the top player left on the board was the second RB. However, A had already drafted an RB, meaning they had to select either the 0-pointer QB or WR. In the end, the result was: 4 points for A, 7 points for B and 5 points for C. As noted by solver Jane Steele of Santa Clara, California, this outcome was worse for A, so we expected A to take the top QB rather than the top RB with their first pick.

In the end, person B came out on top, which meant picking second in the draft was indeed your best option. Returning to the original point scale, that meant A and C both had 800 points, while B had 825 points. With a team of McChristian, Kurray and Hyreek Till, drafting second would indeed have made you unstoppable.
-----------------------------------------------

Problem #2
First off, as noted by solvers Christopher Green and Jenny Mitchell, this pursuit problem was very similar to a prior riddle about an angry ram that chased you out of a pen. Yours truly almost took home that week’s coolest extension award, losing out to Lex K.

Solver Chris Sears used approximation methods to numerically determine the speed that would just catch Jarrison. As you can see from the animation below, Chris found your speed had to be somewhere around 19.2 miles per hour.
[Sorry, not animated]


Several solvers, like Dan Swenson, Rajeev Pakalapati and Laurent Lessard, were able to find more precise solutions by setting up differential equations to describe the motion of you and Jarrison and then solving these equations using calculus.

As with the riddle of the ram from five years ago, it was also possible to solve without using calculus, as demonstrated by Allen Gu. Allen noted the similar triangles formed by your velocity and Jarrison’s velocity at any given moment, shown below.



This meant the ratio of your vertical speed (i.e., in the direction from one end zone to the other) to his total speed was equal to the ratio of Jarrison’s speed away from you to his actual speed running down the sideline.

Before moving further, let’s rescale the field and the speeds. Suppose your starting position is (0, 0), while Jarrison starts at (1, 0) and is moving toward (0, 2). Then suppose Jarrison’s speed is 1 and your speed is v. (The final solution will then be v multiplied by 15 miles per hour.)

The initial distance between you and Jarrison was 1, which fell to zero by the time you caught him at the goal line at time 2. During this time, you pursued him at speed v, bringing you closer by a distance 2v. However, Jarrison was also running away from you by a net distance of 2/v. (You can show this by integrating your vertical speed over time, which had to come out to a distance of 2, and then scaling down by a factor of v.) Writing these changes in distance as an equation, Allen found that it was quadratic: 1 = 2v−2/v, or 2v2−v−2 = 0.

Applying the quadratic formula, v came out to be (1+√17)/4. Scaling back to the original values of the problem, your speed had to be this many times greater than 15 miles per hour, or about 19.2116 miles per hour — very nearly the result from Chris’s approximation.

Jarrison had better hope that your name isn’t Usain Bolt or Tyreek Hill. But maybe they’ll be too busy racing each other to worry about catching Jarrison.

Quote: Gialmere

Quote: charliepatrick

Quote: Gialmere

......Which draft position should you choose to maximize your expected fantasy score?...

Show Spoiler

Pick B.

A's best strategy is to pick QB400. B has a choice of QB350 or RB300.
(i) In the former C is now guaranteed QB300 so picks RB300 and WR250, B will choose WR225 over RB225. A=800, B=775, C=850.
(ii) In the latter C chooses QB350 and RB250, B then chooses WR225 and will eventually get QB300. A=800, B=825, C=800.

So by choosing B and RB300 you get 825.

link to original post

Correct!!

Quote: ChesterDog

Quote: Gialmere

Still in play...

Quote: Gialmere

From Riddler 538 comes this pair of football puzzles...



Problem #2
Hames Jarrison has just intercepted a pass at one end zone of a football field, and begins running — at a constant speed of 15 miles per hour — to the other end zone, 100 yards away.

At the moment he catches the ball, you are on the very same goal line, but on the other end of the field, 50 yards away from Jarrison. Caught up in the moment, you decide you will always run directly toward Jarrison’s current position, rather than plan ahead to meet him downfield along a more strategic course.

Assuming you run at a constant speed (i.e., don’t worry about any transient acceleration), how fast must you be in order to catch Jarrison before he scores a touchdown?
link to original post

link to original post

Show Spoiler

Since it's an easy math problem, I used an easy method of numerical approximation. I started at (0, 50) and Jarrison started at (0, 0). Starting at t = 0 seconds, I ran toward (0,0). Starting at t = 0.0025 seconds, I ran toward the position reached by Jarrison at t = 0.0025 seconds, which was (0.1833, 0), and so on until Jarrison and I reached (100, 0) simultaneously.

This method gave me an answer of about 19.21 miles per hour.

link to original post

Correct!!

Official Solves

Problem #1
Here’s what Riddler Nation had to say:

19.9 percent of readers said they would draft first.
62.3 percent of readers said they would draft second.
17.7 percent of readers said they would draft third.

The majority opted to draft second. But was that the best strategy?

At first glance, some readers thought Osh Jallen (350 points) was a better pick than Caffrey McChristian (300 points). However, missing out on Jallen meant you could grab Myler Kurray, who was only 50 points lower. Meanwhile, missing out on McChristian meant that your running back, at best, was 75 points lower. So while Jallen had more expected points, McChristian was the more valuable pick in the draft.

To better make sense of this, it was helpful to rescale all the expected point values, as solver Johnny of Toronto, Canada, did. All that mattered were the relative differences between the scores. One way to rescale them was to say that the lowest-scoring player at each position was worth 0 points, and that every 25 “original” points were worth 1 “rescaled” point. That meant the quarterbacks (QBs) were respectively worth 4, 2 and 0 points; the running backs (RBs) were worth 4, 1 and 0 points; and the wide receivers (WRs) were worth 3, 2 and 0 points.

Person A’s best move was to grab one of the 4-pointers — either the top QB or the top RB. Suppose they picked the top QB, which meant B picked the top RB, giving them 4 points apiece. From there, C would pick the top WR for 3 points as well as the second QB for 2 points, netting them 5 points in total (since the third picks were all worth 0 points). Because of the snake draft ordering, B got the next pick. They would have snagged the top remaining player, which was the second WR for another 2 points. Finally, A would have drafted the second RB for 1 point. During the final round, each person would have drafted the position they needed to complete their roster. For this scenario, the final result was: 5 points for A, 6 points for B and 5 points for C.

Drafting second was looking good so far. But what if person A had opted for the other 4-pointer, the top RB?

In this case, B would have taken the top QB. The picks for C would have remained the same: the top WR and the second QB, for a total of 5 points. Once again, B then picked the second WR. At this point, the top player left on the board was the second RB. However, A had already drafted an RB, meaning they had to select either the 0-pointer QB or WR. In the end, the result was: 4 points for A, 7 points for B and 5 points for C. As noted by solver Jane Steele of Santa Clara, California, this outcome was worse for A, so we expected A to take the top QB rather than the top RB with their first pick.

In the end, person B came out on top, which meant picking second in the draft was indeed your best option. Returning to the original point scale, that meant A and C both had 800 points, while B had 825 points. With a team of McChristian, Kurray and Hyreek Till, drafting second would indeed have made you unstoppable.
-----------------------------------------------

Problem #2
First off, as noted by solvers Christopher Green and Jenny Mitchell, this pursuit problem was very similar to a prior riddle about an angry ram that chased you out of a pen. Yours truly almost took home that week’s coolest extension award, losing out to Lex K.

Solver Chris Sears used approximation methods to numerically determine the speed that would just catch Jarrison. As you can see from the animation below, Chris found your speed had to be somewhere around 19.2 miles per hour.
[Sorry, not animated]


Several solvers, like Dan Swenson, Rajeev Pakalapati and Laurent Lessard, were able to find more precise solutions by setting up differential equations to describe the motion of you and Jarrison and then solving these equations using calculus.

As with the riddle of the ram from five years ago, it was also possible to solve without using calculus, as demonstrated by Allen Gu. Allen noted the similar triangles formed by your velocity and Jarrison’s velocity at any given moment, shown below.



This meant the ratio of your vertical speed (i.e., in the direction from one end zone to the other) to his total speed was equal to the ratio of Jarrison’s speed away from you to his actual speed running down the sideline.

Before moving further, let’s rescale the field and the speeds. Suppose your starting position is (0, 0), while Jarrison starts at (1, 0) and is moving toward (0, 2). Then suppose Jarrison’s speed is 1 and your speed is v. (The final solution will then be v multiplied by 15 miles per hour.)

The initial distance between you and Jarrison was 1, which fell to zero by the time you caught him at the goal line at time 2. During this time, you pursued him at speed v, bringing you closer by a distance 2v. However, Jarrison was also running away from you by a net distance of 2/v. (You can show this by integrating your vertical speed over time, which had to come out to a distance of 2, and then scaling down by a factor of v.) Writing these changes in distance as an equation, Allen found that it was quadratic: 1 = 2v−2/v, or 2v2−v−2 = 0.

Applying the quadratic formula, v came out to be (1+√17)/4. Scaling back to the original values of the problem, your speed had to be this many times greater than 15 miles per hour, or about 19.2116 miles per hour — very nearly the result from Chris’s approximation.

Jarrison had better hope that your name isn’t Usain Bolt or Tyreek Hill. But maybe they’ll be too busy racing each other to worry about catching Jarrison.

----------------------------------------------

Tom Brady is an optimistic type of player.

He sees the football as being half full.
link to original post

Quote: GM

Quote: aceside

Quote: GM

Quote: aceside

I am thinking in 2D. To have a non-zero integer solution, we must have tan(t)=sin(t)/cos(t)=m/n, as a fraction. In this problem, tan(t)=(m/n)Sqrt(7/3), is not a fraction; therefore, there is no solution.
link to original post

If this type of argument worked, it would also work if you changed the coefficient 3 to 2 in the equation. However, X^2=2Y^2+7Z^2 has non-trivial solutions, for example, X=3, Y=1, Z=1.
link to original post

Interesting! For a general quadric surface equation x^2=a*y^2+b*z^2, what integer coefficients a and b can make non-zero integer solutions happen?
link to original post

I think this is due to the French mathematician Legendre.

First, we can reduce it to the case when neither of a, b is divisible by the square of an integer other than 1. If n^2 divides a and X=u, Y=v, Z=w is a solution of X^2=aY^2+bZ^2, then X=u, Y=nv, Z=w is a solution of X^2=(a/n^2)Y^2+bZ^2, and if X=r, Y=s, Z=t is a solution of X^2=(a/n^2)Y^2+bZ^2, then X=nr, Y=s, Z=nt is a solution of X^2=aY^2+bZ^2. Therefore X^2=aY^2+bZ^2 has a non-trivial integer solution if and only is X^2=(a/n^2)Y^2+bZ^2 has. Of course, we can do the same thing with b.

Let’s assume that neither of a, b is divisible by the square of an integer other than 1.
The equation X^2=aY^2+bZ^2 has a non-trivial integer solutions if and only if the following 4 conditions are satisfied:
(i) at least one of a, b is positive,
(ii) if p is an odd prime (i.e., other than 2) dividing a, then there exists an integer k such that k^2-b is divisible by p,
(iii) if p is an odd prime p dividing b, then there exists an integer k such that k^2-a is divisible by p,
(iv) At least one of a and b gives remainder 1 on division by 8, or their remainders are (2,2), (2,6), (6,2), (2,7), (7,2), (3,5), (5,3), (3,6), (6,3), (5,5) or (6,6).

It is relatively easy to prove that these conditions are necessary (search for quadratic residues and Legendre symbols) and it is easy to determine whether the integer k in (ii) and (iii) exists even for large primes, the hard part is to prove that if these conditions are satisfied, then there exists a non-trivial solution.
link to original post

Quote: ThatDonGuy

Quote: teliot

For any integer N, consider the list of all primes that are in the half-open interval (N/2,N]. Call them p1, p2, p3 ... , pk. The question is, for which N is N!/(p1*p2*p3*...*pk) a perfect square? In other words, divide N! by all the primes greater than N/2 and less than or equal to N (the Bertrand's Postulate primes) and ask if what's leftover is a perfect square.

Any others? Infinitely many? This isn't in the OEIS (at least that I can find).
link to original post

I wrote something that can calculate for larger numbers, and have not found any others for any N < 2000.
link to original post