Easy math puzzles
Poll
 | 21 votes (45.65%) | ||
| | 14 votes (30.43%) | ||
| | 6 votes (13.04%) | ||
| | 3 votes (6.52%) | ||
| | 12 votes (26.08%) | ||
| | 3 votes (6.52%) | ||
| | 6 votes (13.04%) | ||
| | 5 votes (10.86%) | ||
| | 12 votes (26.08%) | ||
| | 10 votes (21.73%) |
46 members have voted
December 29th, 2020 at 8:52:17 AM
permalink
Quote: rsactuaryIf I were Adam or Chris in this situation, I would vote against it, knowing that Bob and Dave for sure will vote against it. Then Ernie walks the plank, and they have a better chance of more coins. Seems to satisfy the requirements, yes?
If you are referencing my second answer, you can go back and look at my first attempt. I explain my reasoning there (albeit with a flawed final answer, hence the revision).
I think Adam or Chris would only get less in future rounds, so priority rule #1 would have them vote yes and accept Ernie's offer.
December 29th, 2020 at 1:04:59 PM
permalink
Quote: rsactuaryIf I were Adam or Chris in this situation, I would vote against it, knowing that Bob and Dave for sure will vote against it. Then Ernie walks the plank, and they have a better chance of more coins. Seems to satisfy the requirements, yes?
As a reminder, the correct answer for Ernie's suggestion, starting with Adam, is 2-0-1-0-997. It will get a vote of Y-N-Y-N-Y.
If Chris votes against it, then Dave would suggest 1-2-0-997, which would get a vote of Y-Y-N-Y. In that scenario, Chris gets nothing. He is better off voting yes to Ernie's suggestion and getting one gold coin.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 29th, 2020 at 1:14:01 PM
permalink
In the following figure there are five rectangles, all of equal area, inscribed in a square. The short side of the yellow rectangle is 1. What is the area of each rectangle?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 29th, 2020 at 2:24:32 PM
permalink
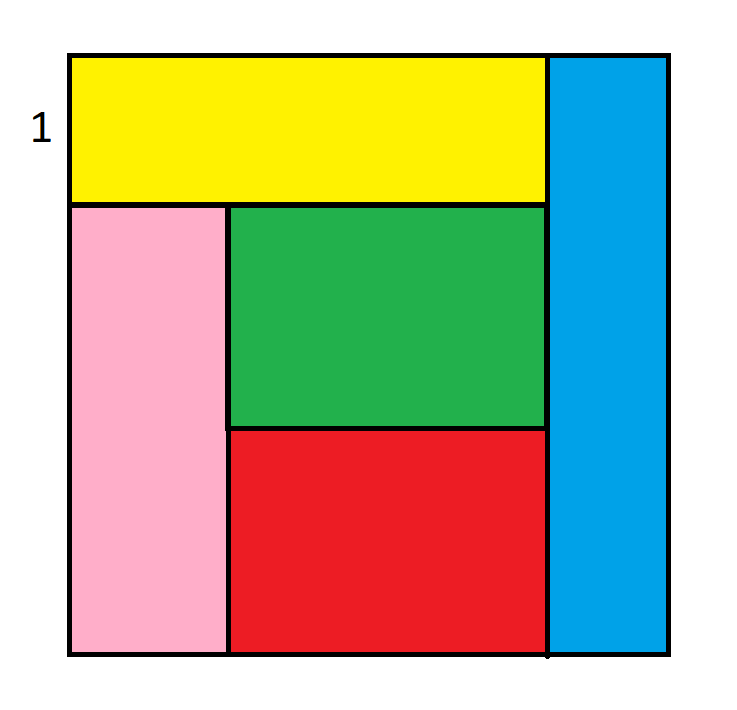
Area of each rectangle = 16/5
a=width of pink
b=width of green
c=height of pink
d=height of green
Then
A(yellow)=A(pink)=A(green)=A(red)=A(blue)
1*(a+b) = ac = bd = (c-d)*b = (1+c)*(1+c-a-b)
Four equations (one for each equal sign). solve
a=16/15, b=32/15, c=3, d=3/2
Common area = ac = 48/15 = 16/5 (area of pink for example)
December 29th, 2020 at 2:36:21 PM
permalink
Let x^2 be the area of each rectangle; the area of the square is 5 x^2, so the area of each rectangle = sqrt(5) x.
The area of the yellow rectangle = 1 * the long side length = x^2, so the yellow triangle's long side has length x^2.
This means the short side of the blue rectangle has length sqrt(5) x - x^2.
The long side of the blue triangle has length sqrt(5) x, so its area = sqrt (5) x * (sqrt(5) x - x^2) = x^2.
sqrt(5) x^2 * (sqrt(5) - x) = x^2
sqrt(5) * (sqrt(5) - x) = 1 = 5 - sqrt(5) x
sqrt(5) x = 4
x = 4 / sqrt(5)
The area of each rectangle = x^2 = 16/5
December 29th, 2020 at 4:05:01 PM
permalink
Both chevy and Don are correct! Well done gentlemen.
I got this one from one of my favorite YouTubers, Presh Talwalkar.
Direct: https://www.youtube.com/watch?v=lrND8AeL23s
Let a = Short side of the blue rectangle.
The long side of the yellow rectangle must be 4a, because the area of the sum of the yellow, pink, green, and red rectangles is four times the blue rectangle and both that sum of those four rectangles and the blue rectangle have the same height.
The area of the yellow rectangle is thus 1*4a = 4a.
The length of a side of the square is a + 4a = 5a.
The area of the whole square is (5a)^2 = 25a^2.
Five times the yellow rectangle equals the whole square:
5*4a = 25a^2
Divide both sides by 5a:
4 = 5a
a = 4/5.
The area of the whole square is thus 25*(4/5)^2 = 16.
The area of each rectangle is thus 16/5 = 3.2
I got this one from one of my favorite YouTubers, Presh Talwalkar.
Direct: https://www.youtube.com/watch?v=lrND8AeL23s
Let a = Short side of the blue rectangle.
The long side of the yellow rectangle must be 4a, because the area of the sum of the yellow, pink, green, and red rectangles is four times the blue rectangle and both that sum of those four rectangles and the blue rectangle have the same height.
The area of the yellow rectangle is thus 1*4a = 4a.
The length of a side of the square is a + 4a = 5a.
The area of the whole square is (5a)^2 = 25a^2.
Five times the yellow rectangle equals the whole square:
5*4a = 25a^2
Divide both sides by 5a:
4 = 5a
a = 4/5.
The area of the whole square is thus 25*(4/5)^2 = 16.
The area of each rectangle is thus 16/5 = 3.2
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 29th, 2020 at 5:59:17 PM
permalink
Here's a Slightly Tougher Math Problem: it does require some calculus.
You are asked, as a homework problem, "What is the largest number with Googol (i.e. 10^100) decimal digits?", and you decide that, rather than just say, "Googolplex - 1", you want to "write out" the answer to your hard drive - all 10^100 digits (all of which are 9s) of it.
If you start now, your hard drive can write 10^10 decimal digits per second, so it would take 10^90 seconds, or a little more than 3 x 10^82 years, to write the whole thing. However, as technology improves, if you wait, you can then use a faster hard drive. The speed of hard drives is increasing exponentially, and doubles every 10^8 seconds, which is a little more than 3 years. In other words, if you wait t seconds before starting, the hard drive speed will be 10^10 x 2^(t / 10^8) digits per second. Eventually, you will reach a point where any additional waiting time would be longer than the time saved by waiting.
What is the shortest amount of total time (waiting + writing) in which the number can be written in full?
Bonus question (some math if you want there to be, but mainly physics): what's the primary flaw with this idea?
You are asked, as a homework problem, "What is the largest number with Googol (i.e. 10^100) decimal digits?", and you decide that, rather than just say, "Googolplex - 1", you want to "write out" the answer to your hard drive - all 10^100 digits (all of which are 9s) of it.
If you start now, your hard drive can write 10^10 decimal digits per second, so it would take 10^90 seconds, or a little more than 3 x 10^82 years, to write the whole thing. However, as technology improves, if you wait, you can then use a faster hard drive. The speed of hard drives is increasing exponentially, and doubles every 10^8 seconds, which is a little more than 3 years. In other words, if you wait t seconds before starting, the hard drive speed will be 10^10 x 2^(t / 10^8) digits per second. Eventually, you will reach a point where any additional waiting time would be longer than the time saved by waiting.
What is the shortest amount of total time (waiting + writing) in which the number can be written in full?
Bonus question (some math if you want there to be, but mainly physics): what's the primary flaw with this idea?
December 29th, 2020 at 6:18:54 PM
permalink
In general, the flaw is that the time to store information cannot decrease endlessly. A specific limit is the plank time (approximately 5.4x 10-44 seconds) at which the uncertainty in the information becomes larger than the information.
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
December 29th, 2020 at 8:32:08 PM
permalink
Quote: gordonm888
In general, the flaw is that the time to store information cannot decrease endlessly. A specific limit is the plank time (approximately 5.4x 10-44 seconds) at which the uncertainty in the information becomes larger than the information.
10^100 decimal digits take 3.322 x 10^100 bits to store.
Since the radius of a sphere varies as the cube root of its volume, multiplying the radius of a sphere by 10^(100/3) multiplies the volume by 10^100, so the minimum possible radius of a spherical hard drive needed to store the entire number = 2.1544 x 10^33 times the radius of whatever is needed to store a bit.
Assuming the hard drive consists entirely of neutrons tightly packed together (assuming this is even possible), a neutron has a radius of 8 x 10^(-16) m, so the radius of the hard drive is 1.7235 x 10^15 km, or about 182 light years. Even if you could build one that large, it would take 182 light years for the last few digits to be written to the far edges of the drive.
December 29th, 2020 at 8:33:12 PM
permalink
T = total time = t + 10^100 / (10^10 * 2^(t/10^8)) = t + 10^90 * 2^(-t/10^8)
Set dT/dt=0
1+10^90 * (-1/10^8) ln(2) 2^(-t/10^8) = 0
1=10^82 ln(2) 2^(-t/10^8)
2^(t/10^8) = 10^82 ln(2)
(t/10^8) ln(2) = ln[10^82 ln(2)]
t = 10^8 ln[10^82 ln(2)] / ln(2)
t=271.869 * 10^8 sec.............this looks suspiciously close to e * 10^10........maybe rounding error in my calc?
So total time
T = 271.869 * 10^8 + 1/ln(2) * 10^8
T= 273.312 * 10^8 sec
T = 2.73312*10^10 sec ~ 866.667 years
Comments:
1) it is local minimum since ThatDonGuy said it was....and because this is less than with wait time = 0 and as wait time --> infinity
2) If my algebra is correct and write time reduces to 1/ln(2) * 10^8.....it suggest my algebra was not the most efficient and perhaps an easier simplification in solving for t exists.
December 30th, 2020 at 9:40:01 PM
permalink
Proof that 1=2:
Let a=b
a^2 = ab (multiplying both sides by a)
a^2 - b^2 = ab - b^2 (subtracting b^2 from each side)
(a+b)*(a-b) = b*(a-b)
a+b = b (divide both side by a-b)
2b = b (substitute b for a)
2 = 1 (divide both sides by b)
Where is the error in my logic?
Let a=b
a^2 = ab (multiplying both sides by a)
a^2 - b^2 = ab - b^2 (subtracting b^2 from each side)
(a+b)*(a-b) = b*(a-b)
a+b = b (divide both side by a-b)
2b = b (substitute b for a)
2 = 1 (divide both sides by b)
Where is the error in my logic?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 31st, 2020 at 12:38:41 AM
permalink
Quote: WizardProof that 1=2:
Let a=b
a^2 = ab (multiplying both sides by a)
a^2 - b^2 = ab - b^2 (subtracting b^2 from each side)
(a+b)*(a-b) = b*(a-b)
a+b = b (divide both side by a-b)
2b = b (substitute b for a)
2 = 1 (divide both sides by b)
Where is the error in my logic?
Divide by ZERO !
December 31st, 2020 at 12:43:47 AM
permalink
He even did it twice!Quote: ssho88Divide by ZERO !
2b=b implies b=0 not 2=1!
December 31st, 2020 at 7:54:38 AM
permalink
Quote: ssho88
Divide by ZERO !
Correct!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 31st, 2020 at 8:37:35 AM
permalink
You have a six-sided red die with 3 sides labeled red, 1 labeled blue and 2 labeled green.
You have a six-sided blue die with 2 sides labeled red, 2 labeled blue and 2 labeled green.
You have a six-sided green die with 1 side labeled red, 4 labeled blue and 1 labeled green.
Whatever you roll on any die shall determine which die you roll next.
You start out with the red die.
You keep rolling forever.
What ratio of rolls are done with each die?
You have a six-sided blue die with 2 sides labeled red, 2 labeled blue and 2 labeled green.
You have a six-sided green die with 1 side labeled red, 4 labeled blue and 1 labeled green.
Whatever you roll on any die shall determine which die you roll next.
You start out with the red die.
You keep rolling forever.
What ratio of rolls are done with each die?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 31st, 2020 at 9:50:40 AM
permalink
Quote: WizardYou have a six-sided red die with 3 sides labeled red, 1 labeled blue and 2 labeled green.
You have a six-sided blue die with 2 sides labeled red, 2 labeled blue and 2 labeled green.
You have a six-sided green die with 1 side labeled red, 4 labeled blue and 1 labeled green.
Whatever you roll on any die shall determine which die you roll next.
You start out with the red die.
You keep rolling forever.
What ratio of rolls are done with each die?
R : B : G = 6 : 7 : 5
Just my wild guess.
December 31st, 2020 at 9:55:46 AM
permalink
Quote: ssho88
R : B : G = 6 : 7 : 5
Just my wild guess.
I disagree.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 31st, 2020 at 4:33:36 PM
permalink
Define a "run" as a sequence of consecutive die rolls that start with a red die and end with a red side being rolled
(so the next die to be rolled would be red).
Since the number of rolls is infinite, the ratio of rolls of each die is the ratio of the expected number
of rolls each die within a run.
Let R, B, and G be the expected number of rolls remaining in the run if the current die being rolled is red, blue, or green, respectively.
Let (r,b,g) be the number of red, blue, and green rolls in the current run.
R = (1, 0, 0) + 1/6 B + 1/3 G
If the current die is blue, the expected number of blue-side rolls before a non-blue side is rolled is
2/3 x (0 + 1/3 x 1 + (1/3)^2 x 2 + ...)
= 2/3 x 1/3 x (1 + 1/3 x 2 + (1/3)^2 x 3 + ...)
= 2/9 x (1 + 1/3 + (1/3)^2 + ...)^2
= 2/9 x (3/2)^2
= 1/2
1/2 of the time, the first non-blue side is red, and 1/2 of the time, it is green
B = (0, 1, 0) + (0, 1/2, 0) + 1/2 G = (0, 3/2, 0) + 1/2 G
If the current die is green, the expected number of green-side rolls before a non-green side is rolled is
5/6 x (0 + 1/6 x 1 + (1/6)^2 x 2 + ...)
= 5/6 x 1/6 x (1 + 1/6 x 2 + (1/6)^2 x 3 + ...)
= 5/36 x (1 + 1/6 + (1/6)^2 + ...)^2
= 5/36 x (6/5)^2
= 1/5
1/5 of the time, the first non-green side is red, and 4/5 of the time, it is blue
G = (0, 0, 1) + (0, 0, 1/5) + 4/5 B = (0, 0, 6/5) + 4/5 B
= (0, 0, 6/5) + 4/5 (0, 3/2, 0) + 2/5 G
3/5 G = (0, 6/5, 6/5)
G = (0, 2, 2)
B = (0, 3/2, 0) + 1/2 G = (0, 3/2, 0) + 1/2 (0, 2, 2) = (0, 5/2, 1)
R = (1, 0, 0) + 1/6 B + 1/3 G = (1, 0, 0) + 1/6 (0, 5/2, 3) + 1/3 (0, 2, 1)
= (1, 13/12, 5/6)
The ratio of red : blue : green = 12 : 13 : 10
December 31st, 2020 at 6:19:46 PM
permalink
Let R(x)=probability of being Red on turn x; similarly B(x) G(x).
Then the next roll, it could be red having come from Red, Blue or Green.
R(x+1)=R(x)*3/6 + B(x)*2/6 + G(x)*1/6.
The chances of being Red (or other colours) on one turn should be the same as on the next turn, i.e. R(x+1) should be the same as R(x).
For here on using R G and B.
Consequently multiplying both sides by 6.
(1) 6R = 3R+2B+G; 3R=2B+G
(2) 6B = R+2B+4G;
(3) 6G = 2R+2B+1G
Using (1) 3R=2B+G
(2)x3 18B=3R+6B+12G = 8B+13G.
10B=13G.
(1)x5: 15R=10B+5G=18G
10R=12G.
So the ratio is Green 10: Red 12: Blue 13.
Then the next roll, it could be red having come from Red, Blue or Green.
R(x+1)=R(x)*3/6 + B(x)*2/6 + G(x)*1/6.
The chances of being Red (or other colours) on one turn should be the same as on the next turn, i.e. R(x+1) should be the same as R(x).
For here on using R G and B.
Consequently multiplying both sides by 6.
(1) 6R = 3R+2B+G; 3R=2B+G
(2) 6B = R+2B+4G;
(3) 6G = 2R+2B+1G
Using (1) 3R=2B+G
(2)x3 18B=3R+6B+12G = 8B+13G.
10B=13G.
(1)x5: 15R=10B+5G=18G
10R=12G.
So the ratio is Green 10: Red 12: Blue 13.
December 31st, 2020 at 7:17:03 PM
permalink
Charlie & Don -- I agree!
Hope you enjoyed the problem. I found it pretty difficult too and subject to error.
This one is definitely beer worthy, to both of you.
Happy new year!
Hope you enjoyed the problem. I found it pretty difficult too and subject to error.
This one is definitely beer worthy, to both of you.
Happy new year!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 3rd, 2021 at 9:47:17 AM
permalink
Quote: chevy
T = total time = t + 10^100 / (10^10 * 2^(t/10^8)) = t + 10^90 * 2^(-t/10^8)
Set dT/dt=0
1+10^90 * (-1/10^8) ln(2) 2^(-t/10^8) = 0
1=10^82 ln(2) 2^(-t/10^8)
2^(t/10^8) = 10^82 ln(2)
(t/10^8) ln(2) = ln[10^82 ln(2)]
t = 10^8 ln[10^82 ln(2)] / ln(2)
t=271.869 * 10^8 sec.............this looks suspiciously close to e * 10^10........maybe rounding error in my calc?
So total time
T = 271.869 * 10^8 + 1/ln(2) * 10^8
T= 273.312 * 10^8 sec
T = 2.73312*10^10 sec ~ 866.667 years
Comments:
1) it is local minimum since ThatDonGuy said it was....and because this is less than with wait time = 0 and as wait time --> infinity
2) If my algebra is correct and write time reduces to 1/ln(2) * 10^8.....it suggest my algebra was not the most efficient and perhaps an easier simplification in solving for t exists.
Correct.
I get the same value for t: 10^8 (82 ln 10 + ln (ln 2)) / ln 2.
ln (10^82 ln 2) = ln (10^82) + ln (ln 2) = 82 ln 10 + ln (ln 2).
For those of you playing at home, note that if f(x) = a^x for some positive real number a, df/dx = a^x ln a.
Since dT/dt has only one zero point, it is either a maximum, a minimum, or an inflection point.
At t = 0, T = 10^90 > 10^10
At t = 10^11, T > 10^11 > 10^10
Therefore, T is a minumum where dT/dt = 0.
Alternatively, take the second derivative of T:
d^2T/dt^2 = -10^82 ln 2 * (2^(-(10^-8))^t * ln (2^(-(10^-8))
= -10^82 ln 2 * (2^(-(10^-8))^t * (-(10^-8)) ln 2
= 10^74 (ln 2)^2 * (2^(-(10^-8))^t
This > 0 for all t, so dT/dt = 0 is a minimum.
January 4th, 2021 at 2:18:34 PM
permalink
Starting from a come out roll, what is the expected number of rolls for all six points to be won? The points can be won by various shooters
It’s all about making that GTA
January 5th, 2021 at 3:00:12 PM
permalink
Easy math, right?
This year, 2021, is the product of consecutive primes: 2021 = 43*47.
What was the year before this one that was the product of consecutive primes?
What is the next year that will be the product of consecutive primes?
What is the next year that will be the product of twin primes (primes that differ by 2)?
Is every finite group of order 2021 cyclic?
And in the year 1202 (2021 backwards), Fibonacci wrote his famous book Liber Abaci (Book of Abacus or The Book of Calculation), which popularized Hindu–Arabic numerals in Europe and first explained the utility of the Fibonacci sequence for calculating rabbit populations. (thanks Wikipedia!)
In other words, 2021 is very special.
This year, 2021, is the product of consecutive primes: 2021 = 43*47.
What was the year before this one that was the product of consecutive primes?
What is the next year that will be the product of consecutive primes?
What is the next year that will be the product of twin primes (primes that differ by 2)?
Is every finite group of order 2021 cyclic?
And in the year 1202 (2021 backwards), Fibonacci wrote his famous book Liber Abaci (Book of Abacus or The Book of Calculation), which popularized Hindu–Arabic numerals in Europe and first explained the utility of the Fibonacci sequence for calculating rabbit populations. (thanks Wikipedia!)
In other words, 2021 is very special.
Last edited by: teliot on Jan 5, 2021
Climate Casino: https://climatecasino.net/climate-casino/
January 5th, 2021 at 3:24:02 PM
permalink
The last one before 2021 was also the last one (and the first since 899) to be a prime pair:
1763 = 41 x 43
The next one is:
2491 = 47 x 53
The next prime pair is:
3599 = 59 x 61
The only other prime pair before 10,000 is:
5183 = 71 x 73
January 5th, 2021 at 5:18:46 PM
permalink
Yes. And thanks for your 10,000 answer.Quote: ThatDonGuy
The last one before 2021 was also the last one (and the first since 899) to be a prime pair:
1763 = 41 x 43
The next one is:
2491 = 47 x 53
The next prime pair is:
3599 = 59 x 61
The only other prime pair before 10,000 is:
5183 = 71 x 73
What about that cyclic group question? And, if Fibonacci was correct about rabbits and we started with two rabbits in 1202, how many rabbits would we have today?
Climate Casino: https://climatecasino.net/climate-casino/
January 5th, 2021 at 5:49:51 PM
permalink
Quote: teliotWhat about that cyclic group question? And, if Fibonacci was correct about rabbits and we started with two rabbits in 1202, how many rabbits would we have today?
Group theory is a little above my math pay grade.
As for Fibonacci, given that his problem specified that rabbits breed every month (except for their first month, I get, at the end of the 9828th month:
61,663,903,718,616,908,525,832,683,988
,551,651,393,900,081,202,751,092,380,950,215,566,662,244,207
,284,750,440,519,578,393,588,447,614,735,878,375,794,896,673
,274,514,678,510,451,799,646,640,898,584,844,359,660,921,952
,068,794,519,569,421,864,294,836,756,628,011,880,354,423,856
,116,428,594,717,113,792,571,646,410,720,910,229,221,446,096
,672,177,466,398,165,302,139,176,956,673,875,869,873,856,661
,936,473,679,366,046,684,037,573,614,161,599,244,469,508,447
,929,172,932,399,012,382,057,061,668,036,598,817,830,201,665
,224,884,876,468,036,003,712,273,382,911,548,687,051,790,739
,514,476,747,916,403,971,270,195,378,786,500,815,293,965,865
,801,209,875,431,666,331,747,346,115,806,258,701,975,985,829
,260,476,870,971,415,698,776,733,543,961,383,983,620,459,615
,669,012,191,317,339,037,600,121,121,255,637,261,858,612,792
,926,221,936,783,685,806,225,716,254,054,667,093,530,428,914
,267,379,047,100,176,392,176,251,489,991,745,056,866,698,332
,425,126,200,016,294,309,522,479,701,327,300,042,515,792,950
,302,083,721,160,766,866,074,277,218,879,169,563,234,968,285
,429,439,015,220,721,475,010,428,876,777,937,770,681,685,843
,188,428,926,710,450,827,786,132,382,379,071,494,507,578,169
,572,746,899,190,405,997,109,942,054,345,947,212,298,054,489
,717,275,675,760,015,895,418,376,483,190,974,576,419,527,316
,764,651,703,858,243,325,729,124,337,830,723,048,331,973,802
,417,852,046,917,567,028,503,180,837,023,707,802,339,694,972
,150,401,284,793,060,942,917,981,803,968,272,470,750,650,466
,544,449,421,119,090,825,825,272,008,137,267,940,410,700,812
,956,708,987,685,722,577,025,503,176,516,424,364,051,583,655
,446,346,356,838,042,979,799,030,620,396,270,123,765,302,092
,051,949,907,917,257,557,788,999,094,170,729,236,153,624,878
,257,045,670,580,700,482,856,717,944,986,952,247,405,838,218
,761,175,992,545,972,752,326,472,603,300,539,634,321,155,949
,430,567,074,223,211,355,252,938,944,678,182,463,179,356,178
,824,187,261,456,390,158,424,491,991,202,585,308,836,850,984
,649,147,783,401,368,105,827,180,488,876,804,419,833,439,459
,883,001,408,424,459,974,600,815,056,554,525,031,418,869,901
,435,095,440,868,684,957,323,255,719,478,934,220,478,001,045
,522,785,742,630,470,022,349,192,569,155,075,955,919,898,677
,808,665,046,634,221,443,717,722,483,277,957,817,586,380,981
,534,033,239,133,697,074,464,904,345,390,789,063,092,335,323
,886,031,743,098,106,868,678,548,564,110,177,926,345,923,719
,592,298,939,624,002,204,984,926,913,610,626,006,668,864,521
,808,553,050,825,192,928,223,905,603,275,231,246,492,130,162
,498,040,633,542,103,528,194,102,611,732,895,205,837,649,890
,738,420,684,184,123,291,262,112,187,863,160,333,730,632,712
,748,899,685,743,507,353,078,611,474,006,633,102,733,937,136
,354,476,686,142,902,541,336,014,399,319,029,954,775,873,529
That's 2054 digits
January 5th, 2021 at 5:52:33 PM
permalink
Love that you did this to the exact rabbit.Quote: ThatDonGuyGroup theory is a little above my math pay grade.
As for Fibonacci, given that his problem specified that rabbits breed every month (except for their first month, I get, at the end of the 9828th month:
61,663,903,718,616,908,525,832,683,988
,551,651,393,900,081,202,751,092,380,950,215,566,662,244,207
,284,750,440,519,578,393,588,447,614,735,878,375,794,896,673
,274,514,678,510,451,799,646,640,898,584,844,359,660,921,952
,068,794,519,569,421,864,294,836,756,628,011,880,354,423,856
,116,428,594,717,113,792,571,646,410,720,910,229,221,446,096
,672,177,466,398,165,302,139,176,956,673,875,869,873,856,661
,936,473,679,366,046,684,037,573,614,161,599,244,469,508,447
,929,172,932,399,012,382,057,061,668,036,598,817,830,201,665
,224,884,876,468,036,003,712,273,382,911,548,687,051,790,739
,514,476,747,916,403,971,270,195,378,786,500,815,293,965,865
,801,209,875,431,666,331,747,346,115,806,258,701,975,985,829
,260,476,870,971,415,698,776,733,543,961,383,983,620,459,615
,669,012,191,317,339,037,600,121,121,255,637,261,858,612,792
,926,221,936,783,685,806,225,716,254,054,667,093,530,428,914
,267,379,047,100,176,392,176,251,489,991,745,056,866,698,332
,425,126,200,016,294,309,522,479,701,327,300,042,515,792,950
,302,083,721,160,766,866,074,277,218,879,169,563,234,968,285
,429,439,015,220,721,475,010,428,876,777,937,770,681,685,843
,188,428,926,710,450,827,786,132,382,379,071,494,507,578,169
,572,746,899,190,405,997,109,942,054,345,947,212,298,054,489
,717,275,675,760,015,895,418,376,483,190,974,576,419,527,316
,764,651,703,858,243,325,729,124,337,830,723,048,331,973,802
,417,852,046,917,567,028,503,180,837,023,707,802,339,694,972
,150,401,284,793,060,942,917,981,803,968,272,470,750,650,466
,544,449,421,119,090,825,825,272,008,137,267,940,410,700,812
,956,708,987,685,722,577,025,503,176,516,424,364,051,583,655
,446,346,356,838,042,979,799,030,620,396,270,123,765,302,092
,051,949,907,917,257,557,788,999,094,170,729,236,153,624,878
,257,045,670,580,700,482,856,717,944,986,952,247,405,838,218
,761,175,992,545,972,752,326,472,603,300,539,634,321,155,949
,430,567,074,223,211,355,252,938,944,678,182,463,179,356,178
,824,187,261,456,390,158,424,491,991,202,585,308,836,850,984
,649,147,783,401,368,105,827,180,488,876,804,419,833,439,459
,883,001,408,424,459,974,600,815,056,554,525,031,418,869,901
,435,095,440,868,684,957,323,255,719,478,934,220,478,001,045
,522,785,742,630,470,022,349,192,569,155,075,955,919,898,677
,808,665,046,634,221,443,717,722,483,277,957,817,586,380,981
,534,033,239,133,697,074,464,904,345,390,789,063,092,335,323
,886,031,743,098,106,868,678,548,564,110,177,926,345,923,719
,592,298,939,624,002,204,984,926,913,610,626,006,668,864,521
,808,553,050,825,192,928,223,905,603,275,231,246,492,130,162
,498,040,633,542,103,528,194,102,611,732,895,205,837,649,890
,738,420,684,184,123,291,262,112,187,863,160,333,730,632,712
,748,899,685,743,507,353,078,611,474,006,633,102,733,937,136
,354,476,686,142,902,541,336,014,399,319,029,954,775,873,529
That's 2054 digits
And a little bit of Fibonacci trivia, the largest Fibonacci number that is a perfect square is 144.
Climate Casino: https://climatecasino.net/climate-casino/
January 5th, 2021 at 6:15:46 PM
permalink
Quote: teliotAnd a little bit of Fibonacci trivia, the largest Fibonacci number that is a perfect square is 144.
Also, the largest one that is a triangular/triangle (I always called them triangle numbers, but I am under the impression that triangular is the proper term) is 55. This was actually a question in this year's Old Farmer's Almanac, but it has the wrong answer (it says 21).
January 8th, 2021 at 8:31:01 PM
permalink
Here is the Mensa logic/math puzzle for January 2021.
Amy and Bob play 20 rounds of rock paper scissors. There were no ties.
Amy played, in no particular order, rock 3 times, paper 6 times, and scissors 11 times.
Bob player, in no particular order, rock 6 times, paper 5 times, and scissors 9 times.
How many games did each player win?
Amy and Bob play 20 rounds of rock paper scissors. There were no ties.
Amy played, in no particular order, rock 3 times, paper 6 times, and scissors 11 times.
Bob player, in no particular order, rock 6 times, paper 5 times, and scissors 9 times.
How many games did each player win?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 8th, 2021 at 8:52:30 PM
permalink
Amy wins 3 rock against scissors
Amy loses 6 paper against scissors
Amy wins 5 scissors against paper
Amy loses 6 scissors against rock
Total
Amy wins 8, Bob wins 12.
(Because no ties, Bob's 9 scissors must be against Amy's rock and paper (3+6=9). Leaving Amy's 11 scissors against Bob's rock and paper (6+5=11))
January 9th, 2021 at 4:06:59 AM
permalink
Quote: chevy
Amy wins 3 rock against scissors
Amy loses 6 paper against scissors
Amy wins 5 scissors against paper
Amy loses 6 scissors against rock
Total
Amy wins 8, Bob wins 12.
(Because no ties, Bob's 9 scissors must be against Amy's rock and paper (3+6=9). Leaving Amy's 11 scissors against Bob's rock and paper (6+5=11))
I agree!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 9th, 2021 at 4:19:40 AM
permalink
Quote: Ace2Starting from a come out roll, what is the expected number of rolls for all six points to be won? The points can be won by various shooters
This one was asked in Ask the Wizard #331.
The answer is 8706865474775503638338329687/39730260732259873692189000 = Approximation: 219.1494672902
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 16th, 2021 at 12:06:20 PM
permalink
Suppose you play a game with a die where you roll and sum your rolls. You may stop any time, and the sum is your score. However, if your sum is ever a multiple of 10, your score is zero and the game is over.
What strategy will yield the greatest expected score?
Have you tried 22 tonight? I said 22.
January 16th, 2021 at 12:31:27 PM
permalink
Quote: GialmereSuppose you play a game with a die where you roll and sum your rolls. You may stop any time, and the sum is your score. However, if your sum is ever a multiple of 10, your score is zero and the game is over.
What strategy will yield the greatest expected score?
My first thought was, "Is there one? At any time, either the probability of losing is 1/6 (if the current score mod 10 is between 4 and 9 inclusive) or zero."
However, I did find one through simulation if the strategy is assumed to be, "Stop if your score is (some particular number) or higher."
I'd like to see a mathematical explanation for this answer - especially if the actual strategy is different (say, "Stop after X rolls if your score is Y or higher"):
The best strategy appears to be, stop if your score is 24 or higher. This barely beats out stopping at 34 or higher.
January 16th, 2021 at 1:01:34 PM
permalink
I'm not sure how to solve this without resorting to a spreadsheet so here goes.
Initially consider the last digit of your current total. If you have 1, 2, 3 then you cannot lose. If you have 4,5,6,7,8,9 then the average score by rolling is the next six numbers but then ignoring the multiple of 10. There comes a point where the risk of losing what you've got means you should stop rolling.
The method of working it our is to use recursion and work out the EVs, whether it's best to stand or hit (think Blackjack!).
For instance on 34 your EV is (35+36+37+38+39+0)/6 = 30 5/6 - so you should stop on 34.
However 39 is different because if you get, say, 41 you reroll, so it's value is 45.76 (this is because of the additional chances of going via 42 and 43). So the EV is (0+45.76+46.08+46.5+44+45)/6 = 37.89. It's a closer decision, but you still still stop.
In the 20's this effect does change your decision.
So you hit 21, 22, 23. Working back from 29 you hit 26-29, but stand on 24 and 25.
The net EV seems to be 13.217 (I'm sure someone can work out the really long fraction!)
Summary
Hit 23 or less.
Stand on 24 or 25.
Hit 26 to 33.
Stand on 34 or more.
The method of working it our is to use recursion and work out the EVs, whether it's best to stand or hit (think Blackjack!).
For instance on 34 your EV is (35+36+37+38+39+0)/6 = 30 5/6 - so you should stop on 34.
However 39 is different because if you get, say, 41 you reroll, so it's value is 45.76 (this is because of the additional chances of going via 42 and 43). So the EV is (0+45.76+46.08+46.5+44+45)/6 = 37.89. It's a closer decision, but you still still stop.
In the 20's this effect does change your decision.
So you hit 21, 22, 23. Working back from 29 you hit 26-29, but stand on 24 and 25.
The net EV seems to be 13.217 (I'm sure someone can work out the really long fraction!)
Summary
Hit 23 or less.
Stand on 24 or 25.
Hit 26 to 33.
Stand on 34 or more.
January 16th, 2021 at 5:53:04 PM
permalink
Quote: charliepatrickI'm not sure how to solve this without resorting to a spreadsheet so here goes.
Initially consider the last digit of your current total. If you have 1, 2, 3 then you cannot lose. If you have 4,5,6,7,8,9 then the average score by rolling is the next six numbers but then ignoring the multiple of 10. There comes a point where the risk of losing what you've got means you should stop rolling.
The method of working it our is to use recursion and work out the EVs, whether it's best to stand or hit (think Blackjack!).
For instance on 34 your EV is (35+36+37+38+39+0)/6 = 30 5/6 - so you should stop on 34.
However 39 is different because if you get, say, 41 you reroll, so it's value is 45.76 (this is because of the additional chances of going via 42 and 43). So the EV is (0+45.76+46.08+46.5+44+45)/6 = 37.89. It's a closer decision, but you still still stop.
In the 20's this effect does change your decision.
So you hit 21, 22, 23. Working back from 29 you hit 26-29, but stand on 24 and 25.
The net EV seems to be 13.217 (I'm sure someone can work out the really long fraction!)
Summary
Hit 23 or less.
Stand on 24 or 25.
Hit 26 to 33.
Stand on 34 or more.
Correct!
:strip_icc()/pic5920492.png)
----------------------------------
I lost my kids' college fund playing dice in Vegas.
I admit it was a crappy thing to do.
Have you tried 22 tonight? I said 22.
January 17th, 2021 at 6:21:15 PM
permalink
From 538 this week comes this puzzle:
You’re a contestant on the hit new game show, “You Bet Your Fife.” On the show, a random real number (i.e., decimals are allowed) is chosen between 0 and 100. Your job is to guess a value that is less than this randomly chosen number. Your reward for winning is a novelty fife that is valued precisely at your guess. For example, if the number is 75 and you guess 5, you’d win a $5 fife, but if you’d guessed 60, you’d win a $60 fife. Meanwhile, a guess of 80 would win you nothing.
What number should you guess to maximize the average value of your fifing winnings?
My gut instinct tells me the answer should be 49.999999 (9 repeating), but I'm guessing that that is too easy an answer. Given that a real number is chosen, I'm assuming that some calculus is involved.
So if the number selected is "n" and our guess is "x", then I thought about I could solve this as the integral from 0 to n of (x) times (x/100) (value of the win times the probability of the win). Then taking the derivative of the function with respect to n to determine the maximum. That's not working. What am I missing?
You’re a contestant on the hit new game show, “You Bet Your Fife.” On the show, a random real number (i.e., decimals are allowed) is chosen between 0 and 100. Your job is to guess a value that is less than this randomly chosen number. Your reward for winning is a novelty fife that is valued precisely at your guess. For example, if the number is 75 and you guess 5, you’d win a $5 fife, but if you’d guessed 60, you’d win a $60 fife. Meanwhile, a guess of 80 would win you nothing.
What number should you guess to maximize the average value of your fifing winnings?
My gut instinct tells me the answer should be 49.999999 (9 repeating), but I'm guessing that that is too easy an answer. Given that a real number is chosen, I'm assuming that some calculus is involved.
So if the number selected is "n" and our guess is "x", then I thought about I could solve this as the integral from 0 to n of (x) times (x/100) (value of the win times the probability of the win). Then taking the derivative of the function with respect to n to determine the maximum. That's not working. What am I missing?
January 17th, 2021 at 6:27:53 PM
permalink
Quote: Gialmere
Suppose you play a game with a die where you roll and sum your rolls. You may stop any time, and the sum is your score. However, if your sum is ever a multiple of 10, your score is zero and the game is over.
What strategy will yield the greatest expected score?
That die appears to have two 2's and two 3's and no five or six.
At my age, a "Life In Prison" sentence is not much of a deterrent.
January 17th, 2021 at 7:07:28 PM
permalink
If you pick $75 then there's a 25% chance of winning. Similarly if you pick $25, there's a 75% chance of winning. Generally speaking if you pick $X then there's a (100-X)% chance of winning, and the EV is the same as picking $(100-X) with X% of winning.
Now think that 49*51 is 50*50-1 (50-1)*(50+1). So the best value to pick is $50, as you have a 50% chance of winning (EV=$25).
Using calculus
EV=100x-x2
d(EV)/dx = 100 - 2x. This is zero when x=50.
Now think that 49*51 is 50*50-1 (50-1)*(50+1). So the best value to pick is $50, as you have a 50% chance of winning (EV=$25).
Using calculus
EV=100x-x2
d(EV)/dx = 100 - 2x. This is zero when x=50.
January 18th, 2021 at 6:59:08 AM
permalink
Quote: charliepatrickIf you pick $75 then there's a 25% chance of winning. Similarly if you pick $25, there's a 75% chance of winning. Generally speaking if you pick $X then there's a (100-X)% chance of winning, and the EV is the same as picking $(100-X) with X% of winning.
Now think that 49*51 is 50*50-1 (50-1)*(50+1). So the best value to pick is $50, as you have a 50% chance of winning (EV=$25).
Using calculus
EV=100x-x2
d(EV)/dx = 100 - 2x. This is zero when x=50.
Thanks... I set up my integrand incorrectly.
January 18th, 2021 at 1:41:07 PM
permalink
Tuesday Puzzle (one day early)
The casino has a new dice game.
The prize to be won in each round is 11 units. Each roll of a die costs the player 4 units.
The player rolls one die at a time.
- if the sum of the dice equals exactly 4 OR "10 or higher" (>9), the player wins 11 units and the game stops. Reset to another round.
- if the sum of the dice equals 1-3 or 5-9 then player may roll an additional die for another 4 units. The sum of the dice is now recalculated to include all of the dice that player has rolled in that round.
As long as the player keeps rolling dice (as he should) he/she will always win 11 units each round. The unknown in any round is how much he will spend on dice to win the 11 units.
What is the house edge of this game?
The casino has a new dice game.
The prize to be won in each round is 11 units. Each roll of a die costs the player 4 units.
The player rolls one die at a time.
- if the sum of the dice equals exactly 4 OR "10 or higher" (>9), the player wins 11 units and the game stops. Reset to another round.
- if the sum of the dice equals 1-3 or 5-9 then player may roll an additional die for another 4 units. The sum of the dice is now recalculated to include all of the dice that player has rolled in that round.
As long as the player keeps rolling dice (as he should) he/she will always win 11 units each round. The unknown in any round is how much he will spend on dice to win the 11 units.
What is the house edge of this game?
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
January 18th, 2021 at 2:59:20 PM
permalink
Quote: gordonm888Tuesday Puzzle (one day early)
The casino has a new dice game.
The prize to be won in each round is 11 units. Each roll of a die costs the player 4 units.
The player rolls one die at a time.
- if the sum of the dice equals exactly 4 OR "10 or higher" (>9), the player wins 11 units and the game stops. Reset to another round.
- if the sum of the dice equals 1-3 or 5-9 then player may roll an additional die for another 4 units. The sum of the dice is now recalculated to include all of the dice that player has rolled in that round.
As long as the player keeps rolling dice (as he should) he/she will always win 11 units each round. The unknown in any round is how much he will spend on dice to win the 11 units.
What is the house edge of this game?
Let E(n) be the expected number of rolls needed to win with a score of n.
Determine the expected number of rolls
E(4) = E(10) = E(11) = E(12) = E(13) = E(14) = E(15) = 0
E(9) = 1
E(8) = 1 + 1/6 E(9)
= 7/6
E(7) = 1 + 1/6 (E(8) + E(9))
= 1 + 1/6 x 13/6
= 49/36
E(6) = 1 + 1/6 (E(7) + E(8) + E(9))
= 1 + 1/6 x 127/36
= 343/216
E(5) = 1 + 1/6 (E(6) + E(7) + E(8) + E(9))
= 1 + 1/6 x 1105/216
= 2401/1296
E(3) = 1 + 1/6 (E(5) + E(6) + E(7) + E(8) + E(9))
= 1 + 1/6 (2401 + 2058 + 1764 + 1512 + 1296 )/1296
= 16,807/7776
E(2) = 1 + 1/6 (E(3) + E(5) + E(6) + E(7) + E(8))
= 1 + 1/6 (16,807 + 14,406 + 12,348 + 10,584 + 9072)/7776
= 109,873 / 46,656
E(1) = 1 + 1/6 (E(2) + E(3) + E(5) + E(6) + E(7))
= 1 + 1/6 (109,873 + 100,842 + 86,436 + 74,088 + 63,504)/46,656
= 714,649 / 279,936
E(0) = 1 + 1/6 (E(1) + E(2) + E(3) + E(5) + E(6))
= 1 + 1/6 (714,649 + 659,238 + 605,052 + 518,616 + 444,528)/279,936
= 4,621,699 / 1,679,616
The expected wager = 4 x the number of rolls = 4,621,699 / 419,904
The expected return is 11
The house edge = (expected wager - expected return) / expected wager
= 2755 / 419,904 = 0.6561%
January 18th, 2021 at 4:49:43 PM
permalink
Quote: ThatDonGuyQuote: gordonm888Tuesday Puzzle (one day early)
The casino has a new dice game.
The prize to be won in each round is 11 units. Each roll of a die costs the player 4 units.
The player rolls one die at a time.
- if the sum of the dice equals exactly 4 OR "10 or higher" (>9), the player wins 11 units and the game stops. Reset to another round.
- if the sum of the dice equals 1-3 or 5-9 then player may roll an additional die for another 4 units. The sum of the dice is now recalculated to include all of the dice that player has rolled in that round.
As long as the player keeps rolling dice (as he should) he/she will always win 11 units each round. The unknown in any round is how much he will spend on dice to win the 11 units.
What is the house edge of this game?
Let E(n) be the expected number of rolls needed to win with a score of n.
Determine the expected number of rolls
E(4) = E(10) = E(11) = E(12) = E(13) = E(14) = E(15) = 0
E(9) = 1
E(8) = 1 + 1/6 E(9)
= 7/6
E(7) = 1 + 1/6 (E(8) + E(9))
= 1 + 1/6 x 13/6
= 49/36
E(6) = 1 + 1/6 (E(7) + E(8) + E(9))
= 1 + 1/6 x 127/36
= 343/216
E(5) = 1 + 1/6 (E(6) + E(7) + E(8) + E(9))
= 1 + 1/6 x 1105/216
= 2401/1296
E(3) = 1 + 1/6 (E(5) + E(6) + E(7) + E(8) + E(9))
= 1 + 1/6 (2401 + 2058 + 1764 + 1512 + 1296 )/1296
= 16,807/7776
E(2) = 1 + 1/6 (E(3) + E(5) + E(6) + E(7) + E(8))
= 1 + 1/6 (16,807 + 14,406 + 12,348 + 10,584 + 9072)/7776
= 109,873 / 46,656
E(1) = 1 + 1/6 (E(2) + E(3) + E(5) + E(6) + E(7))
= 1 + 1/6 (109,873 + 100,842 + 86,436 + 74,088 + 63,504)/46,656
= 714,649 / 279,936
E(0) = 1 + 1/6 (E(1) + E(2) + E(3) + E(5) + E(6))
= 1 + 1/6 (714,649 + 659,238 + 605,052 + 518,616 + 444,528)/279,936
= 4,621,699 / 1,679,616
The expected wager = 4 x the number of rolls = 4,621,699 / 419,904
The expected return is 11
The house edge = (expected wager - expected return) / expected wager
= 2755 / 419,904 = 0.6561%
CORRECT
I get that player will invest 11.006561 units to win 11 units, so exact agreement.
| Number of dice used | ___Probability___ |
|---|---|
| 1 | 0.16666667 |
| 2 | 0.22222222 |
| 3 | 0.36574074 |
| 4 | 0.19135803 |
| 5 | 0.04681070 |
| 6 | 0.00660151 |
| 7 | 0.00057156 |
| 8 | 0.00002798 |
| 9 | 0.00000060 |
There are 1221 distinct outcomes for player (of widely varying probability) ranging from 4 to 111211116
Let me praise ThatDonGuy for extremely clear answers that are easy to understand and check! I am learning some good math techniques by reading his answers on this thread.
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
January 18th, 2021 at 5:21:22 PM
permalink
I used EVs at different scores, so looked for the EV at 0. I get a slightly different answer of -2785/419904 = -0.006632. However you now have to divide that by 4 since that is the overall cost for a 4 unit wager. So House Edge = 0.1658%.
Method 1 is to use the EVs of 15 to 10 being 11.
At each stage the EV of a number is the average of the next six numbers less the cost of 4 to make the additional roll.
Thus the EV at 9 is (EV(10)+EV(11)+EV(12)+EV(13)+EV(14)+EV(15))/6-4 = 7.
Repeat and rinse except when at 4 the EV(4) = 11.
Method 2 keeps the numbers
EV(9) = 7 (as above)
EV(8) = (11+11+11+11+11+7)/6-4 = 38/6
EV(7) = 200/36
EV(6) = 1004/216
EV(5) = 4652/1296
EV(4) = 11
EV(3) = 18308/7776
EV(2) = 73724/46656
EV(1) = 220580/279936
EV(0) = -11140/1679616 = -2785/419904 = -0.00663247.
Method 1 is to use the EVs of 15 to 10 being 11.
At each stage the EV of a number is the average of the next six numbers less the cost of 4 to make the additional roll.
Thus the EV at 9 is (EV(10)+EV(11)+EV(12)+EV(13)+EV(14)+EV(15))/6-4 = 7.
Repeat and rinse except when at 4 the EV(4) = 11.
Method 2 keeps the numbers
EV(9) = 7 (as above)
EV(8) = (11+11+11+11+11+7)/6-4 = 38/6
EV(7) = 200/36
EV(6) = 1004/216
EV(5) = 4652/1296
EV(4) = 11
EV(3) = 18308/7776
EV(2) = 73724/46656
EV(1) = 220580/279936
EV(0) = -11140/1679616 = -2785/419904 = -0.00663247.
January 18th, 2021 at 5:36:43 PM
permalink
Looking at your figures I agree with all of them until the very last stage. I get 714639...444528 adding up to 2942113, but then you need to add 1679616 (for the "1") to get 4621729 rather than 4621699. This would then be the same as my figure.Quote: ThatDonGuy...E(0) = 1 + 1/6 (E(1) + E(2) + E(3) + E(5) + E(6))
= 1 + 1/6 (714,649 + 659,238 + 605,052 + 518,616 + 444,528)/279,936
= 4,621,699 / 1,679,616
January 18th, 2021 at 6:41:12 PM
permalink
I agree with your probabilities but...Quote: gordonm888...There are 1221 distinct outcomes for player (of widely varying probability) ranging from 4 to 111211116...
Contribution is $4*no of rolls*probability.
| No of rolls | Times | Probability | Contribution |
|---|---|---|---|
1 | 1 | .166 666 667 | 0.666 666 667 |
2 | 8 | .222 222 222 | 1.777 777 778 |
3 | 79 | .365 740 741 | 4.388 888 889 |
4 | 248 | .191 358 025 | 3.061 728 395 |
5 | 364 | .046 810 700 | 0.936 213 992 |
6 | 308 | .006 601 509 | 0.158 436 214 |
7 | 160 | .000 571 559 | 0.016 003 658 |
8 | 47 | .000 027 983 | 0.000 895 443 |
9 | 6 | .000 000 595 | 0.000 021 433 |
Totals | 1.000 000 000 | 11.006 632 468 |
January 23rd, 2021 at 11:26:12 AM
permalink
Fill in the boxes of the grid below with the other numbers from 1 to 16 by making only the moves of a knight in chess.
The numbers follow each other in numerical order.
Not all of the boxes in the grid will be used. The answer is unique.
:strip_icc()/pic5937566.png)
Have you tried 22 tonight? I said 22.
January 23rd, 2021 at 11:52:26 AM
permalink
--, 14, 9, 4, --
2, 7, 12, 15, 10
13, 16, 3, 8, 5
--, 1, 6, 11, --
other than it was the first walk through I tried, I have not not tried all the other solutions to see at what stage they break down.
January 23rd, 2021 at 12:16:02 PM
permalink
Quote: chevy
--, 14, 9, 4, --
2, 7, 12, 15, 10
13, 16, 3, 8, 5
--, 1, 6, 11, --
other than it was the first walk through I tried, I have not not tried all the other solutions to see at what stage they break down.
Label the squares:
A, 14, 9, 4, B
C, D, E, F, G
H, 16, J, K, M
N, 1, 6, 11, P
(note I, L, and O were not used as they may be confused with numbers)
"Touching" in this case means that the two squares are a knight's move apart
The only empty square touching both 14 and 16 is F, so F = 15
The only empty square touching both 9 and 11 is G, so G = 10
C cannot be 8, as there would be no empty square touching 6 and 8 in which to put 7;
the only other empty square touching 9 is K, so K = 8
The only still-empty sqaure touching both 6 and 8 is D, so D = 7
The only still-empty square touching both 4 and 6 is M, so M = 5
E cannot be 2, as there would be no empty square touching 2 and 4 in which to put 3;
the only other empty square touching 1 is C, so C is 2
The only still-empty square touching both 2 and 4 is J, so J = 3
This leaves 12 and 13; E touches 11, so E = 12, and H touches 12 and 14, so H = 13
The solution is unique
January 23rd, 2021 at 12:31:30 PM
permalink
Quote: chevy
--, 14, 9, 4, --
2, 7, 12, 15, 10
13, 16, 3, 8, 5
--, 1, 6, 11, --
other than it was the first walk through I tried, I have not not tried all the other solutions to see at what stage they break down.
Quote: ThatDonGuy
Label the squares:
A, 14, 9, 4, B
C, D, E, F, G
H, 16, J, K, M
N, 1, 6, 11, P
(note I, L, and O were not used as they may be confused with numbers)
"Touching" in this case means that the two squares are a knight's move apart
The only empty square touching both 14 and 16 is F, so F = 15
The only empty square touching both 9 and 11 is G, so G = 10
C cannot be 8, as there would be no empty square touching 6 and 8 in which to put 7;
the only other empty square touching 9 is K, so K = 8
The only still-empty sqaure touching both 6 and 8 is D, so D = 7
The only still-empty square touching both 4 and 6 is M, so M = 5
E cannot be 2, as there would be no empty square touching 2 and 4 in which to put 3;
the only other empty square touching 1 is C, so C is 2
The only still-empty square touching both 2 and 4 is J, so J = 3
This leaves 12 and 13; E touches 11, so E = 12, and H touches 12 and 14, so H = 13
The solution is unique
Correct!
----------------------------
Have you tried 22 tonight? I said 22.
