Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
Again, choose some positive integer N, and then declare distances of D / N, 2D / N, 3D / N, and so on.
If the treasure is <= D/N away, the distance is 2 D/N
If it is between D/N and 2D/N away, the distance is 2 D/N + 2 x 2 D/N = 2 D/N (1 + 2)
If it is between 2D/N and 3D/N away, the distance is 2 D/N + 2 x 2 D/N + 2 x 3 D/N = 2 D/N (1 + 2 + 3)
...
If it is between (N-1) D/N and D away, the distance is 2 D/N + 2 x 2 D/N + 2 x 3 D/N + ... + 2 x ND/N = 2 D/N (1 + 2 + 3 + ... + N)
Since each of these is equally possible, the expected distance is
1/N x 2D / N x (1 + 3 + 6 + ... + N (N+1) /2)
= 2/3 D x (N + 1) (N + 2) / N
This is a minimum where N = sqrt(2)
It turns out that N = 1 and N = 2 both have an expected distance of 2D, so the two equally efficient answers are:
(a) Start by saying, "I will walk to the North Pole"
(b) Start by saying, "I will walk halfway to the North Pole"; if that is unsuccessful, say, "I will walk to the North Pole"
I will have to see if something like, "I will walk sqrt(2) / 2 of the distance to the North Pole" followed by "I will walk to the North Pole" is a better answer.
Call the maximum distance from the start 1.
Suppose I decide I will make three trips at most. Let a = the distance from the start for the first attempt, and b = the distance from the start for the second attempt.
The probability that I find the treasure on the first attempt is a and the distance walked would be 2a.
The probability that I find the treasure on the second attempt is b - a and the total distance walked would be 2a + 2b.
The probability that I find the treasure on the final attempt is 1 - b and the total distance walked would be 2a + 2b + 2.
The mean distance I would walk would be: D = a (2a) + (b - a)(2a + 2b) + (1-b)(2a + 2b + 2).
Simplifying yields D = 2 + 2a(1 - b).
Since b is less than or equal to 1, D cannot be less than 2. If a = 0, then D = 2. Or if b = 1, D = 2. So, D = 2 is the best that can be done with a max of 3 trips.
D = 2 is also the distance for one trip max or two trips max. And I found the same for four trips max, so I D = 2 is the answer.
What would be good for purposes of discussion is an expected ratio of necessary travel to total travel.
Quote: unJonI have a feeling the answer to this question will contain the term:
1/e
link to original post
Mine doesn't.
If the distance to the treasure is a random number between zero and infinity (if possible) then the expected distance is infinity. So you'd never get there regardless of method usedQuote: WizardLet me emphasize you don't know the maximum distance the treasure could be away. I could be 1 inch and it could be a googleplex miles. So, I prefer to not see any assumptions about a maximum distance. Whatever you assume, the treasure could be further away.
What would be good for purposes of discussion is an expected ratio of necessary travel to total travel.
link to original post
Quote: Ace2If the distance to the treasure is a random number between zero and infinity (if possible) then the expected distance is infinity. So you'd never get there regardless of method usedQuote: WizardLet me emphasize you don't know the maximum distance the treasure could be away. I could be 1 inch and it could be a googleplex miles. So, I prefer to not see any assumptions about a maximum distance. Whatever you assume, the treasure could be further away.
What would be good for purposes of discussion is an expected ratio of necessary travel to total travel.
link to original post
link to original post
It's specified you're in the middle of a desert, so it can't be infinite if there is a middle. You also have a compass to find north which implies a spherical surface with a magnetic field and that excludes infinity too.
Maybe there's a missing specification, that the treasure is in the desert, and if that's so can we use r as the distance from the middle of the desert to its northern limit?
Quote: Ace2Answer: The average rolls to get a six or odd is 6/(1+3) = 1.5. Call this a sequenceQuote: SkinnyTonyHere's one that I got from a YouTube video.
We are going to roll a single 6-sided die repeatedly until a 6 is rolled, and keep track of how many rolls it takes.
So for example, if you rolled a 2, 3, 1, 6, that would be 4 rolls. If you rolled a 6 on the first roll, that would be 1 roll.
What is the average number of rolls needed, conditioned on the fact that all rolls are an even number? In other words, if we throw out all sequences that contain an odd number, what's the average length of the remaining sequences?
So for example, 2, 2, 6 would be 3 rolls. 2, 2, 3, 6 would not count since it includes an odd number (3). Similarly 2, 1, 3, 6 would not count.
link to original post
1/(1+3) chance the six came first and the string ends there. If odd came first (3/4 chance) then an average of six more rolls will be needed to get a six. So 1.5 average rolls to get a six when the six comes first and 7.5 average rolls to get a six when an odd comes first
Check: 1/4 * 1.5 + 3/4 * 7.5 = 6 average rolls to get a six irrespective of even/odd
One would initially assume that you can just consider 2,4,6 which would imply an answer of 3 average rolls to get a six. Assuming this, there is a 1/3 chance of ending a sequence with each roll. In actuality, there is a 4/6 chance of ending a sequence with each roll. The reciprocal (6/4) being the answer
link to original post
Yup, this is the right answer and it's the explanation of "why" that I like -- it's intuitive.
My apologies for posting a problem that already been posted; I haven't read through the whole thread. Also I ran out of posts (10/day for new users) so I couldn't reply to ThatDonGuy's post.
Quote: WizardLet me emphasize you don't know the maximum distance the treasure could be away. I could be 1 inch and it could be a googleplex miles. So, I prefer to not see any assumptions about a maximum distance. Whatever you assume, the treasure could be further away.
What would be good for purposes of discussion is an expected ratio of necessary travel to total travel.
link to original post
FYI (yes, I'm being pedantic) but the numbers are "googol" and "googolplex". "google" is a misspelling of the number by the founders of a certain company (or so the legend goes; perhaps it was intentional; who knows)
As for the question... it seems like we need to know something about the probability distribution of possible distances? I don't think "uniform" works without a maximum possible size of the desert (because no such probability distribution exists).
Quote: WizardI think I need to withdraw the treasure to the north puzzle. In the middle of the night I realized a flaw in my work. Upon redoing the math, I don't get a reasonable answer. I'll keep thinking about it, but I should probably apologize now for wasting your time.
link to original post
Given the "there is no maximum distance" restriction, my best guess would have been, "Determine how far you can walk (round trip) in a single go, and declare half of that distance."
Quote: ThatDonGuyGiven the "there is no maximum distance" restriction, my best guess would have been, "Determine how far you can walk (round trip) in a single go, and declare half of that distance."
link to original post
I'll say that the strategy I'm thinking of is to keep increasing the distance declared by some constant. However, for that constant I run into problems, like imaginary numbers. I'm still tinkering with it.
"The chest that will open if I make a true statement has gold inside of it"
If the "true" chest has the gold, then the statement is true, so the gold chest will open.
If the "false" chest has the gold, then the statement is false, so the gold chest will open.
But, were they made by Bellini and Cellini?
Quote: ThatDonGuy
"The chest that will open if I make a true statement has gold inside of it"
If the "true" chest has the gold, then the statement is true, so the gold chest will open.
If the "false" chest has the gold, then the statement is false, so the gold chest will open.
But, were they made by Bellini and Cellini?
link to original post
I'll accept that. Below is a essentially the same thing but in fewer words.
"The chest with the gold will open."
Quote: Wizard...Below is a essentially the same thing but in fewer words.
"The chest with the gold will open."
link to original post
I think you have to refer to the chest by saying something like "You are the gold chest".
In this case, I think, if it is you've made a true statement so it opens, if it isn't then the statement is false and the other one, with the gold, opens.
Quote: charliepatrickIf you say "the chest with the gold will open" and are standing by the lethal one, then it is entitled to open since you have made a false statement.
I think you have to refer to the chest by saying something like "You are the gold chest".
In this case, I think, if it is you've made a true statement so it opens, if it isn't then the statement is false and the other one, with the gold, opens.
link to original post
Good point. Would you agree the following will work. I'm looking for as short and simple of a statement as possible.
Yes I think that seems to work...Quote: Wizard[... Would you agree the following will work. I'm looking for as short and simple of a statement as possible.
The poison gas is in the false chest.
link to original post
(i) if B=poison then it works, because you've said a true statement so A will open
(ii) if A=poison then it looks like it works: you've erroneously suggested B had the poison and this is false. So B will open.
A logician, whose age you don't know, is trapped in a room. On the locked door is a combination lock, which is the only way out. The lock requires three numbers. A conversation goes as follows with the evil wizard who put him there.
Wizard: The second and third number in the combination are equal or greater than the previous number.
Logician: I need more information.
Wizard: The product of the three numbers is 36.
Logician: I need more information.
Wizard: The sum of the three numbers equals your age.
Logician: I need more information.
Wizard: The last number is unique.
Logician: Thank you, I know the combination.
The logician then enters the combination correctly. What is it?
Then you're told AxBxC=36.
Because 36 has factors 1 2 2 3 3, this means the solution has various possibiilities 149 166 229 236 334. 14,13,13,11,10 : Note that only 166 and 229 have the same sum.
The last statement mean it's 229.
Combining the first two questions, the only possible combinations are 149, 166, 229, 236, and 334.
Of these, the sums of three of these are unique, so the logician would have been able to solve it after the third question.
The two that add up to the same number as another combination are 166 and 229, both of which add up to 13.
Of these, 229 is the only one whose last digit is unique.
Quote: WizardHere is another classic puzzle that probably has been asked here before at some point.
A logician, whose age you don't know, is trapped in a room. On the locked door is a combination lock, which is the only way out. The lock requires three numbers. A conversation goes as follows with the evil wizard who put him there.
Wizard: The second and third number in the combination are equal or greater than the previous number.
Logician: I need more information.
Wizard: The product of the three numbers is 36.
Logician: I need more information.
Wizard: The sum of the three numbers equals your age.
Logician: I need more information.
Wizard: The last number is unique.
Logician: Thank you, I know the combination.
The logician then enters the combination correctly. What is it?
link to original post
Gee, Wiz, you seem to like solving problems that involve an evil wizard… Anything we should know about an alter ego? 😄
Replace “number” with “digit” and “combination” with “permutation”. I understand what you mean and normally I wouldn’t care but such terms should be correct on a math forumQuote: WizardHere is another classic puzzle that probably has been asked here before at some point.
A logician, whose age you don't know, is trapped in a room. On the locked door is a combination lock, which is the only way out. The lock requires three numbers. A conversation goes as follows with the evil wizard who put him there.
Wizard: The second and third number in the combination are equal or greater than the previous number.
Logician: I need more information.
Wizard: The product of the three numbers is 36.
Logician: I need more information.
Wizard: The sum of the three numbers equals your age.
Logician: I need more information.
Wizard: The last number is unique.
Logician: Thank you, I know the combination.
The logician then enters the combination correctly. What is it?
link to original post
Quote: Ace2Replace “number” with “digit” and “combination” with “permutation”. I understand what you mean and normally I wouldn’t care but such terms should be correct on a math forumQuote: WizardHere is another classic puzzle that probably has been asked here before at some point.
A logician, whose age you don't know, is trapped in a room. On the locked door is a combination lock, which is the only way out. The lock requires three numbers. A conversation goes as follows with the evil wizard who put him there.
Wizard: The second and third number in the combination are equal or greater than the previous number.
Logician: I need more information.
Wizard: The product of the three numbers is 36.
Logician: I need more information.
Wizard: The sum of the three numbers equals your age.
Logician: I need more information.
Wizard: The last number is unique.
Logician: Thank you, I know the combination.
The logician then enters the combination correctly. What is it?
link to original post
link to original post
That reminds me… I need to procure a permutation lock for my digit warehouse. It’s where I lock up all of my numbers.
The combination is not a palindrome.
Call the combination A. So reverse the digits of the combination to get another 3-digit number B. Subtract the smaller from the larger of B and A to get the difference C.
Now reverse the digits of C to get the number D. Add C and D, and the sum is 1089.
What is the combination?
Quote: AutomaticMonkeyNow what if a monkey hands you a 3-digit combination lock,
link to original post
This seems to work for any three-digit number. I smell a new magic trick!
Let the original number be ABC, (assume A>C). Then reverse it CBA.
ABC-CBA = (A-C)*100-(A-C).
Since this is a three-digit number it must be 200-2, 300-3 etc 900-9, 198 297 396 495 and the reverse of these.
Note that the outside digits add up to 9, and the centre digit is 9.
So when you add 198 to 981, or 297 to 792 etc you are adding the outside digits to get 9, and 9 twice to get 18. Hence this creates 900+180+9 to get 1089.
Thus this works for all numbers where A is greater than C by 2 or more, or their reverse.
Note: for numbers like 102 and 201, the difference is 99 and the end answer is 198, so doesn't satifsy he three-digit rule.
On your first turn you play ABC
You score comes back YXX. For those who don't play, the Y means there is at least one A in the solution but not in the first position. The X's mean there is no B nor C in the solution.
What is the probability the second position is an A?
Quote: Ace2Replace “number” with “digit” and “combination” with “permutation”. I understand what you mean and normally I wouldn’t care but such terms should be correct on a math forumQuote: WizardHere is another classic puzzle that probably has been asked here before at some point.
A logician, whose age you don't know, is trapped in a room. On the locked door is a combination lock, which is the only way out. The lock requires three numbers. A conversation goes as follows with the evil wizard who put him there.
Wizard: The second and third number in the combination are equal or greater than the previous number.
Logician: I need more information.
Wizard: The product of the three numbers is 36.
Logician: I need more information.
Wizard: The sum of the three numbers equals your age.
Logician: I need more information.
Wizard: The last number is unique.
Logician: Thank you, I know the combination.
The logician then enters the combination correctly. What is it?
link to original post
link to original post
I think number still works:
1 1 36 = 38
1 2 18 = 21
1 3 12 = 16
1 4 9 = 14
1 6 6 = 13
2 2 9 = 13
2 3 6 = 11
3 3 4 = 10
Technically integer, but I think ok to assume audience knows what a combination lock is.
Quote: WizardConsider a version of Wordle where it is not required the solution be a word. Before the first turn, every letter is chosen randomly and with replacement for each position. Also, to keep it simple, assume a three-letter words as opposed to five.
On your first turn you play ABC
You score comes back YXX. For those who don't play, the Y means there is at least one A in the solution but not in the first position. The X's mean there is no B nor C in the solution.
What is the probability the second position is an A?
link to original post
Maybe 13/24 is the answer?
Quote: WizardConsider a version of Wordle where it is not required the solution be a word. Before the first turn, every letter is chosen randomly and with replacement for each position. Also, to keep it simple, assume a three-letter words as opposed to five.
On your first turn you play ABC
You score comes back YXX. For those who don't play, the Y means there is at least one A in the solution but not in the first position. The X's mean there is no B nor C in the solution.
What is the probability the second position is an A?
link to original post
I get ..
positions 2 and 3 can be any of AA, AD, AE, ... AZ, DA, EA, ... ZA. The are 47 (equally likely) such combinations. 24 of them have an A in position 2. It's not 50% (24/48) because we don't double count AA.
Quote: WizardConsider a version of Wordle where it is not required the solution be a word. Before the first turn, every letter is chosen randomly and with replacement for each position. Also, to keep it simple, assume a three-letter words as opposed to five.
On your first turn you play ABC
You score comes back YXX. For those who don't play, the Y means there is at least one A in the solution but not in the first position. The X's mean there is no B nor C in the solution.
What is the probability the second position is an A?
link to original post
We know:
(a) There are no Bs or Cs;
(b) There is an A in the second and/or third positions, but not the first
There are 23 "words" with A in the second and third position (DAA through ZAA)
There are 23 x 23 with A in the second position but not the third (DAD-DAZ, EAD-EAZ, ..., ZAD-ZAZ)
There are 23 x 23 with A in the third position but not the second (DDA-DZA, EDA-EZA, ..., ZDA-ZZA)
There are a total of 23 x 47 possible words, of which 23 x 24 have an A in the second position
The probability is 24 / 47
Quote: SkinnyTony
I get ..24/47
positions 2 and 3 can be any of AA, AD, AE, ... AZ, DA, EA, ... ZA. The are 47 (equally likely) such combinations. 24 of them have an A in position 2. It's not 50% (24/48) because we don't double count AA.
link to original post
I agree!
Find an exact expression for the probability that W takes the value 601.
Find an approximation for the probability that W is less than 1845.
Quote: gerback123Mike rolls a fair 4 sided die (tetrahedron) 600 times. Bob tosses a fair coin 600 times. Assume all tosses and rolls are independent. William counts up the total number of dots and heads. Call the sum W
Find an exact expression for the probability that W takes the value 601.
Find an approximation for the probability that W is less than 1845.
link to original post
Interesting puzzle...
600
-----
2^600
Note: I assumed the die has only 1, 2, 3, and 4 dots on its sides.
Quote: gerback123Your assumption is correct, but your answer is not. Good attempt at an interesting puzzle though.
link to original post
Indeed. I agree with you. Haste makes waste. It's about me.
Quote: gerback123Find an exact expression for the probability that W takes the value 601.link to original post
1) 600 die rolls give 1 dot each and only 1 coin toss gives heads
OR
2) 599 die rolls give 1 dot each, 1 die roll gives 2 dots, and 600 coin tosses give tails.
1 600 600 1 1200 75
----- * ----- + ------ * ----- = ------ = ------
4^600 2^600 4^600 2^600 2^1800 2^1796
Quote: gerback123Mike rolls a fair 4 sided die (tetrahedron) 600 times. Bob tosses a fair coin 600 times. Assume all tosses and rolls are independent. William counts up the total number of dots and heads. Call the sum W
Find an exact expression for the probability that W takes the value 601.
Find an approximation for the probability that W is less than 1845.
link to original post
This is the same as rolling an 8-sided die with sides numbered 1, 2, 2, 3, 3, 4, 4, 5 600 times.
The only way to get 601 in 600 rolls is with 599 1s and one 2.
Of the 8^600 = 2^1800 possible sets of rolls, there are 600 (ways for the 2 to appear) x 2 (ways to roll a 2 on a single roll) = 1200 that add up to 601.
The probability = 1200 / 2^1800 = 75 / 2^1796.
Quote:ThatDonGuy
This is the same as rolling an 8-sided die with sides numbered 1, 2, 2, 3, 3, 4, 4, 5 600 times.
The only way to get 601 in 600 rolls is with 599 1s and one 2.
Of the 8^600 = 2^1800 possible sets of rolls, there are 600 (ways for the 2 to appear) x 2 (ways to roll a 2 on a single roll) = 1200 that add up to 601.
The probability = 1200 / 2^1800 = 75 / 2^1796.
I agree!
Quote: gerback123This is the same as rolling an 8-sided die with sides numbered 1, 2, 2, 3, 3, 4, 4, 5 600 times.
link to original post
How did you come to that conclusion?
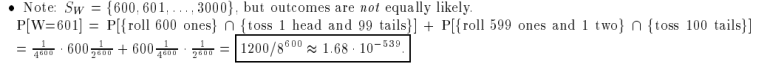
Quote: AnotherBillQuote: gerback123This is the same as rolling an 8-sided die with sides numbered 1, 2, 2, 3, 3, 4, 4, 5 600 times.
link to original post
How did you come to that conclusion?
link to original post
You can match a particular coin toss and a particular die roll into a "pair." Each combination of side of a coin and number on the die has probability 1/8, so this is equivalent to rolling an 8-sided die.
The pairs are (0,1), (0,2), (1,1), (0,3), (1,2), (0,4), (1,3), and (1,4), which are 1, 2, 2, 3, 3, 4, 4, and 5, respectively.
Each toss/roll pair is independent of the others.
Quote: Ace2Your email account receives an average of one email every six minutes, following the exponential distribution. At t=0 minutes, you open your inbox and record the exact amount of time it takes to receive a new email
Starting at t=1 minute, you roll a single six-sided die every minute until you roll a 4. So the sixth roll (if necessary) will occur at t=6 minutes.
link to original post
Quote: Ace2Same scenario, but what’s the expected waiting time for:
1) the first event (email or 4) to happen?
2) both events (email and 4) to happen at least once ?
link to original post
Sorry to resurrect an old problem (I'm really not sorry), but my new and improved answer to #1 is 3.12666037. Not using spoiler tags because I think only Ace and I care.
p.s. Is it just me or is this site slow today?
Site is lagging
Quote: WizardQuote: Ace2Your email account receives an average of one email every six minutes, following the exponential distribution. At t=0 minutes, you open your inbox and record the exact amount of time it takes to receive a new email
Starting at t=1 minute, you roll a single six-sided die every minute until you roll a 4. So the sixth roll (if necessary) will occur at t=6 minutes.
link to original post
Quote: Ace2Same scenario, but what’s the expected waiting time for:
1) the first event (email or 4) to happen?
2) both events (email and 4) to happen at least once ?
link to original post
Agree. The exact answer, which I posted on July-29, is:Quote: WizardSorry to resurrect an old problem (I'm really not sorry), but my new and improved answer to #1 is 3.12666037. Not using spoiler tags because I think only Ace and I care.
p.s. Is it just me or is this site slow today?
link to original post
[(6e^(1/6) - 7)/(e^(1/6) - 1)*(1 - 1/e^(1/6)) + 1/e^(1/6)]/(1 - 5/6*1/e^(1/6))
P.S. other people might care but aren’t capable of solving it
Quote: ThatDonGuyYou can match a particular coin toss and a particular die roll into a "pair."
link to original post
Thank you! Indeed, it is quite straightforward.
Quote: Ace2Agree. The exact answer, which I posted on July-29, is:
[(6e^(1/6) - 7)/(e^(1/6) - 1)*(1 - 1/e^(1/6)) + 1/e^(1/6)]/(1 - 5/6*1/e^(1/6))
P.S. other people might care but aren’t capable of solving it
link to original post
Thank you! I will write up my solution in a PDF document shortly to share.


