Thread Rating:
August 25th, 2013 at 9:53:08 AM
permalink
The probability of NOT having at least 2 consecutive tails in the toss of a coin n times is F(n+2)/2^n, where F(n) is the n-th Fibonacci number.
For those who need a Fibonacci refresher...
F(1)=1
F(2)=1
F(n) = F(n-1) + F(n-2)
Recall here is the first so many Fibonacci numbers.
For example, if you toss a coin 7 times, the probability never getting two or more consecutive tails is f(7+2)/2^7 = 34/128 = 26.56%.
Is there any way we can use Fibonacci to get the probability of never getting 3 (or any other number greater than 2) tails in a row in n flips?
For those who need a Fibonacci refresher...
F(1)=1
F(2)=1
F(n) = F(n-1) + F(n-2)
Recall here is the first so many Fibonacci numbers.
| n | F(n) |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
| 17 | 1597 |
| 18 | 2584 |
| 19 | 4181 |
| 20 | 6765 |
For example, if you toss a coin 7 times, the probability never getting two or more consecutive tails is f(7+2)/2^7 = 34/128 = 26.56%.
Is there any way we can use Fibonacci to get the probability of never getting 3 (or any other number greater than 2) tails in a row in n flips?
"My life is spent in one long effort to escape from the commonplace of existence. These little problems help me to do so." -- Sherlock Holmes
August 25th, 2013 at 10:56:43 AM
permalink
yes.
your example uses a 2 step Fib#,
just use a 3 step Fib#(add last 3 numbers) for 3 in a row and so on
the 9th Fib - 3 step # for your 7 flip example
notation = F3[9]/2^7
where F3[9] is the 9th Fibonacci 3-step number. (aka Tribonacci sequence)
post #9 here
http://forumserver.twoplustwo.com/25/probability/coin-flip-situations-790115/
shows how this is done in Excel
really simple process
only works when p = q = 0.50
also
http://forumserver.twoplustwo.com/25/probability/successes-row-904091/
BruceZ post #7 shows how this is done too
added:
as a check
forgot to add the closed form 2 step Fib formula
from Excel
=(1/sqrt(5))*((((1+sqrt(5))/2)^N)-(((1-sqrt(5))/2)^N))
N=9 for the Wizard's first example on NO 2 tails in a row in 7 flips
hard to imagine that formula returns an integer, but it does
your example uses a 2 step Fib#,
just use a 3 step Fib#(add last 3 numbers) for 3 in a row and so on
the 9th Fib - 3 step # for your 7 flip example
1 1
2 1
3 2
4 4
5 7
6 13
7 24
8 44
9 81
where F3[9] is the 9th Fibonacci 3-step number. (aka Tribonacci sequence)
post #9 here
http://forumserver.twoplustwo.com/25/probability/coin-flip-situations-790115/
shows how this is done in Excel
really simple process
only works when p = q = 0.50
also
http://forumserver.twoplustwo.com/25/probability/successes-row-904091/
BruceZ post #7 shows how this is done too
added:
as a check
matrix algebra time
using a tool here:
http://people.hofstra.edu/Stefan_Waner/RealWorld/matrixalgebra/fancymatrixalg2.html
p and v are for a run of 2 (3 states)
q and r are for a run of 3 (4 states)
enter or copy/paste: p,v,q and r
p=[0.5,0.5,0
0.5,0,0.5
0,0,1]
v=[1,0,0]
q=[0.5,0.5,0,0
0.5,0,0.5,0
0.5,0,0,0.5
0,0,0,1]
r=[1,0,0,0]
now enter
first formula
v*p^7 (fraction mode) press 'compute' returns
v*p^7 =
21/128 13/128 47/64
This shows the 3 states one can be in after 7 flips
(0T,1T or 2T)
so for NO run of 2 tails
1 - state 2T
or sum (state1,state2)
for a run of 3
r*q^7 shows
r*q^7 =
11/32 3/16 13/128 47/128
Now there are 4 states (0T,1T,2T,3T)
1-3T = no run of length 3 in 7 flips
FYI, this matrix algebra tool
one can also add the formulas at the same time as in:
v*p^7,r*q^7
returns
v*p^7 =
21/128 13/128 47/64
r*q^7 =
11/32 3/16 13/128 47/128
nice
I like all the info a matrix returns
also using Rick Parris Winstats program
sim data
parameters:
7 flips
p = 0.50
run of length 2 or greater (>=2)
using a tool here:
http://people.hofstra.edu/Stefan_Waner/RealWorld/matrixalgebra/fancymatrixalg2.html
p and v are for a run of 2 (3 states)
q and r are for a run of 3 (4 states)
enter or copy/paste: p,v,q and r
p=[0.5,0.5,0
0.5,0,0.5
0,0,1]
v=[1,0,0]
q=[0.5,0.5,0,0
0.5,0,0.5,0
0.5,0,0,0.5
0,0,0,1]
r=[1,0,0,0]
now enter
first formula
v*p^7 (fraction mode) press 'compute' returns
v*p^7 =
21/128 13/128 47/64
This shows the 3 states one can be in after 7 flips
(0T,1T or 2T)
so for NO run of 2 tails
1 - state 2T
or sum (state1,state2)
for a run of 3
r*q^7 shows
r*q^7 =
11/32 3/16 13/128 47/128
Now there are 4 states (0T,1T,2T,3T)
1-3T = no run of length 3 in 7 flips
FYI, this matrix algebra tool
one can also add the formulas at the same time as in:
v*p^7,r*q^7
returns
v*p^7 =
21/128 13/128 47/64
r*q^7 =
11/32 3/16 13/128 47/128
nice
I like all the info a matrix returns
also using Rick Parris Winstats program
sim data
parameters:
7 flips
p = 0.50
run of length 2 or greater (>=2)
group middle freq freq/100
---------------------------------------------
-0.5 <= x < 0.50 0.00 2655547 26.56%
0.50 <= x < 1.50 1.00 5939734 59.40%
1.50 <= x < 2.50 2.00 1404719 14.05%
---------------------------------------------
cumulative
---------------------------------------------
-0.5 <= x < 0.50 0.00 2655547 26.56%
0.50 <= x < 1.50 1.00 8595281 85.95%
1.50 <= x < 2.50 2.00 10000000 100.00%
forgot to add the closed form 2 step Fib formula
from Excel
=(1/sqrt(5))*((((1+sqrt(5))/2)^N)-(((1-sqrt(5))/2)^N))
N=9 for the Wizard's first example on NO 2 tails in a row in 7 flips
hard to imagine that formula returns an integer, but it does
winsome johnny (not Win some johnny)
November 3rd, 2013 at 6:11:08 PM
permalink
Quote: 7craps
forgot to add the closed form 2 step Fib formula
from Excel
=(1/sqrt(5))*((((1+sqrt(5))/2)^N)-(((1-sqrt(5))/2)^N))
Ahh the old closed-form Fibonacci. I remember in one of my first discrete math courses we derived that from the recursive definition. Damn I used to be smart back then!
My math professor lamented the fact that in one of our CS courses that term, we were asked to prove the closed form by induction. He felt that wasn't very worthwhile if they just give you the closed form to begin with :)
"So drink gamble eat f***, because one day you will be dust." -ontariodealer
November 4th, 2013 at 5:56:44 AM
permalink
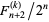
The probability that no k consecutive tails will occur in n tosses is given by EQUATION ABOVE, which the Fibonacci k-step number.
We have actually discussed this equation before. While it is very tight closed form solution, it is numerically unstable as it approaches infinity/infinity for large values of n. It also does not generalize to a weighted coin so that it is useless for calculating streaks with a house edge.
November 5th, 2013 at 10:47:12 AM
permalink
ok, i be different here
so,
one can easily use Pascal's Triangle too
(another very nice guy that died way too young)
to count the number of sequences with NO run of 2
here is the triangle in me Excel (i saw the idea in Excel)
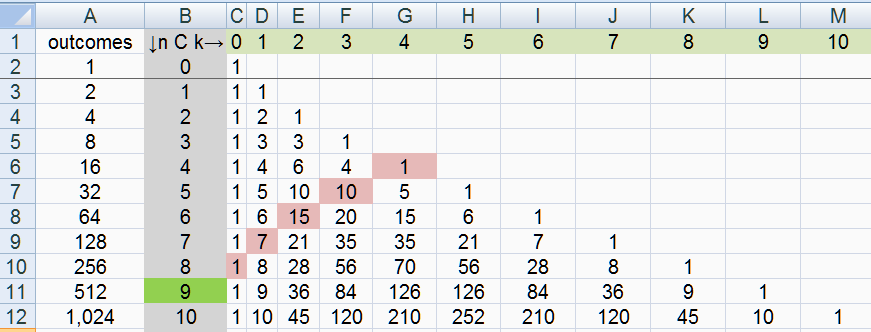
the 9th Fibonacci number = 8C0 + 7C1 + 6C2 +5C3 + 4C4 =
1+7+15+10+1
another nice pattern easily seen
and saves one the heartache of making a math mistake (some do not like making even 1 mistake)
so 34/2^7 = no run
that leaves
(128-34)/2^7 = at least 1 run
Sally
did one of the Wizard's kids ask about Fibonacci numbers
that sparked the idea for this thread?
Kids love Fibonacci numbers
I love this video series
Fibonacci numbers are between 1:10 to 3:00
so,
one can easily use Pascal's Triangle too
(another very nice guy that died way too young)
to count the number of sequences with NO run of 2
here is the triangle in me Excel (i saw the idea in Excel)

the 9th Fibonacci number = 8C0 + 7C1 + 6C2 +5C3 + 4C4 =
1+7+15+10+1
another nice pattern easily seen
and saves one the heartache of making a math mistake (some do not like making even 1 mistake)
so 34/2^7 = no run
that leaves
(128-34)/2^7 = at least 1 run
Sally
did one of the Wizard's kids ask about Fibonacci numbers
that sparked the idea for this thread?
Kids love Fibonacci numbers
I love this video series
Fibonacci numbers are between 1:10 to 3:00
I Heart Vi Hart
December 19th, 2018 at 8:04:46 AM
permalink
I found a formulaic way to solve this kind of problem. On
https://forumserver.twoplustwo.com/25/probability/successes-row-904091/
the example given is the probability of at least one streak of 10 heads given 1,000 coin flips.
The formula is:
1 - r^(k+1)(r-1) / (((n+1)r - 2n)2^k)
Where r is the largest real root of the equation x^n * (2 - x) = 1.
In this case the root of x^10(2 - x) = 1 is 1.9990186327 ....taken to 10 decimal places.
So the probability is:
1 - r^1001(r-1) / ((11r - 20)2^1000) =
38.545 %
https://forumserver.twoplustwo.com/25/probability/successes-row-904091/
the example given is the probability of at least one streak of 10 heads given 1,000 coin flips.
The formula is:
1 - r^(k+1)(r-1) / (((n+1)r - 2n)2^k)
Where r is the largest real root of the equation x^n * (2 - x) = 1.
In this case the root of x^10(2 - x) = 1 is 1.9990186327 ....taken to 10 decimal places.
So the probability is:
1 - r^1001(r-1) / ((11r - 20)2^1000) =
38.545 %
Itís all about making that GTA
December 19th, 2018 at 12:22:24 PM
permalink
Iíd tell you a Fibonacci joke, but itís probably as bad as the last two youíve heard combined.


