James Holzhauer on Jeopardy
May 29th, 2019 at 6:56:20 AM
permalink
Potent Potables last appeared on 5/21/2019, in the Jeopardy Round. This was Holzhauer's 24th show. He ran the category.Quote: AyecarumbaI haven't seen "Potent Potables" as a topic in a long time. Did it fall out of favor?
May 29th, 2019 at 7:11:53 AM
permalink
Some good news regarding Alex Trebek's cancer:
https://www.usatoday.com/story/life/people/2019/05/29/alex-trebek-says-some-his-tumors-have-already-shrunk-50/1268659001/
https://www.usatoday.com/story/life/people/2019/05/29/alex-trebek-says-some-his-tumors-have-already-shrunk-50/1268659001/
Quote:In an interview with People published Wednesday, the "Jeopardy!" host revealed he's in "near remission," according to doctors.
“It’s kind of mind-boggling,” Trebek told the magazine. "The doctors said they hadn’t seen this kind of positive result in their memory … some of the tumors have already shrunk by more than 50%.”
Ding Dong the Witch is Dead
May 29th, 2019 at 7:37:35 AM
permalink
Quote: ams288Some good news regarding Alex Trebek's cancer:
https://www.usatoday.com/story/life/people/2019/05/29/alex-trebek-says-some-his-tumors-have-already-shrunk-50/1268659001/
That’s great news. Pancreatic cancer is generally very aggressive.
May 29th, 2019 at 2:32:38 PM
permalink
Quote: TDVegasThat’s great news. Pancreatic cancer is generally very aggressive.
Jeopardy could save themselves a lot of money by placing the Daily Doubles in the high value questions . Since it is no secret that James picks the highest dollar value first, if the Daily Doubles come to him when he doesn't have much of a bankroll, they can Save a few bucks bucks... if they wanted to.
'Winners hit n run... Losers stick around'
May 29th, 2019 at 3:17:38 PM
permalink
Quote: WatchMeWinJeopardy could save themselves a lot of money by placing the Daily Doubles in the high value questions . Since it is no secret that James picks the highest dollar value first, if the Daily Doubles come to him when he doesn't have much of a bankroll, they can Save a few bucks bucks... if they wanted to.
In the Double Jeopardy round he often starts with the 1200 or 1600 answers.
The other day they had one of the Daily Doubles in the 2000 spot in a “Geography” category. Days earlier, Alex had specifically mentioned that he noticed James is very strong with geography. Coincidence? (Yeah, probably...)
Ding Dong the Witch is Dead
May 29th, 2019 at 7:34:02 PM
permalink
DD Heat Maps
Jeopardy Round Daily Double Locations
Double Jeopardy Daily Double Locations
Jeopardy Round Daily Double Locations
Double Jeopardy Daily Double Locations
Last edited by: SkittleCar1 on May 30, 2019
May 29th, 2019 at 8:18:28 PM
permalink
Yes, if they wanted to. However, I'm not convinced, nor have I seen any evidence, that they want to.Quote: WatchMeWinJeopardy could save themselves a lot of money by placing the Daily Doubles in the high value questions . Since it is no secret that James picks the highest dollar value first, if the Daily Doubles come to him when he doesn't have much of a bankroll, they can Save a few bucks bucks... if they wanted to.
Maybe it's just the opposite. Maybe the prefer having large winners now and then. Maybe they realize someone winning a lot of money means more for long run success of the show.
If no one ever won any large amounts, the game wouldn't be interesting to a lot of people and could die completely.
It's been 14 (or 15) years since Jennings made his historic run. It might be another 14 or 15 before we see a run like this again. If I were in charge of the show, I'd be loving it.
Finally, it's also possible the location of the three daily doubles is random each game. (Not completely random, because so few appear in the top row, but possibly random with some limitations.) If it were up to me, that's exactly what I'd do. I'd eliminate that whole decision on where to place them each game by making their location random, and not worry about it.
May 30th, 2019 at 3:14:30 AM
permalink
Since it appears James knows most of the answers and can buzz in faster than most, is there a mathematical advantage to him to now start at the lower values first?
This would potentially allow him to increase his bank before hitting the DD’s. However it would also open up the chance another player could hit them with a chance to double a higher bank.
What he has done is working, I was just thinking of it for a chance to hit some even higher daily totals.
This would potentially allow him to increase his bank before hitting the DD’s. However it would also open up the chance another player could hit them with a chance to double a higher bank.
What he has done is working, I was just thinking of it for a chance to hit some even higher daily totals.
May 30th, 2019 at 5:52:30 AM
permalink
Quote: SkittleCar1DD Heat Maps
Thanks, that is interesting how they are skewed to the left side. Would you happen to have the exact numbers? I'd like to see what the odds like like.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 30th, 2019 at 6:04:27 AM
permalink
Never mind, I found a this:
I had to do a video capture and then a screen capture towards the end. It's likely there is a little more data, but this is the last frame I could grab. Kind of annoying somebody is going to all this work to collect the information, but the raw numbers don't seem to be easily available.
Source: Where to Find Jeopardy! Daily Doubles
I had to do a video capture and then a screen capture towards the end. It's likely there is a little more data, but this is the last frame I could grab. Kind of annoying somebody is going to all this work to collect the information, but the raw numbers don't seem to be easily available.
Source: Where to Find Jeopardy! Daily Doubles
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 30th, 2019 at 6:22:51 AM
permalink
Sorry to keep replying to myself, but here is a table with those numbers:
I'm assuming the second column top row is zero, although that makes the total not divisible by 3. Have there always been three Daily Doubles per game?
The average total per column is 2276.666667. If we do a chi-squared test of that average against the actual totals we get a value of 578.94 with 5 degrees of freedom. That probability of results that skewed are 1 in 1.39 * 10^122. That is like rolling 97.3 yo's in a row.
Any thoughts on why they favor certain columns and avoid others?
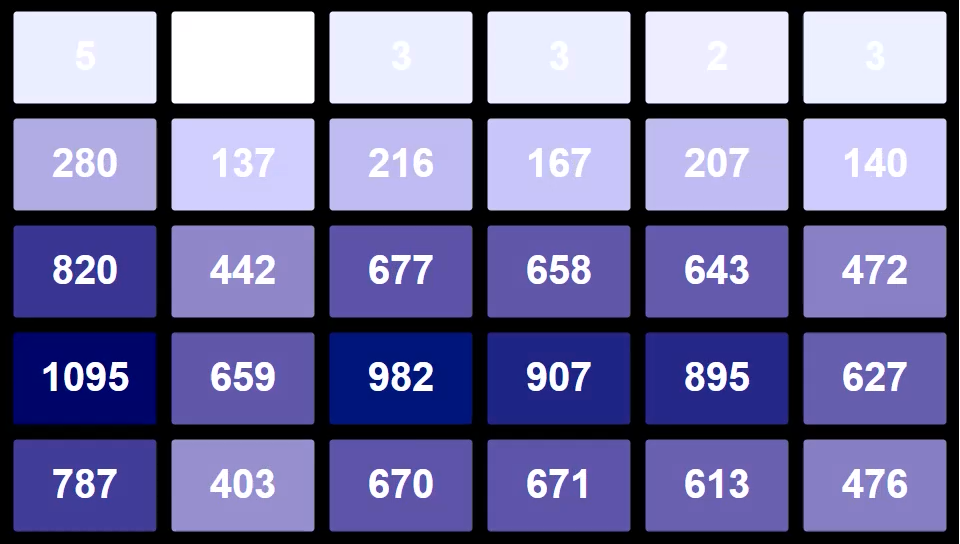
| Daily Doubles | Column 1 | Column 2 | Column 3 | Column 4 | Column 5 | Column 6 | Total |
|---|---|---|---|---|---|---|---|
| Row 1 | 5 | 0 | 3 | 3 | 2 | 3 | 16 |
| Row 2 | 280 | 137 | 216 | 167 | 207 | 140 | 1147 |
| Row 3 | 820 | 442 | 677 | 658 | 643 | 472 | 3712 |
| Row 4 | 1095 | 659 | 982 | 907 | 895 | 627 | 5165 |
| Row 5 | 787 | 403 | 670 | 671 | 613 | 476 | 3620 |
| Total | 2987 | 1641 | 2548 | 2406 | 2360 | 1718 | 13660 |
I'm assuming the second column top row is zero, although that makes the total not divisible by 3. Have there always been three Daily Doubles per game?
The average total per column is 2276.666667. If we do a chi-squared test of that average against the actual totals we get a value of 578.94 with 5 degrees of freedom. That probability of results that skewed are 1 in 1.39 * 10^122. That is like rolling 97.3 yo's in a row.
Any thoughts on why they favor certain columns and avoid others?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 30th, 2019 at 6:34:09 AM
permalink
I found, (edit) slightly different to those above, percentages for the first round and also the second round on this page. I'm guessing those figures are as at 1st May 2019.Quote: WizardNever mind
NB: As they didn't add up when I copied them into a spreadsheet, I factored them to add up to 200%
| Value | Col 1 | Col 2 | Col 3 | Col 4 | Col 5 | Col 6 | Average |
|---|---|---|---|---|---|---|---|
| $400 | 0.04% | 0.02% | 0.10% | 0.04% | 0.02% | 0.00% | 0.04% |
| $800 | 4.43% | 2.54% | 3.54% | 3.20% | 3.44% | 2.42% | 3.26% |
| $1200 | 11.91% | 7.36% | 10.39% | 10.06% | 9.66% | 7.27% | 9.44% |
| $1600 | 15.18% | 10.24% | 14.59% | 12.73% | 14.06% | 9.65% | 12.74% |
| $2000 | 9.17% | 5.67% | 8.93% | 8.47% | 8.51% | 6.37% | 7.85% |
It might be a false observation, but it seems that James isn't always starting on the $2000 squares in the second round. I guess it's more important to find the Daily Doubles before your opponents do. The chances one is in a given square is about 1 in 8 on the $1600 row and next favourite is on the $1200 row.
May 30th, 2019 at 7:04:51 AM
permalink
I wonder why the producers hate the 2nd and last category so much.
May 30th, 2019 at 7:59:11 AM
permalink
Yes, I believe so. Although, I have seen shows where a DD wasn't revealed before the time for that round expired. So totals would not necessarily be a multiple of three.Quote: WizardSorry to keep replying to myself, but here is a table with those numbers:
Daily Doubles Column 1 Column 2 Column 3 Column 4 Column 5 Column 6 Total Row 1 5 0 3 3 2 3 16 Row 2 280 137 216 167 207 140 1147 Row 3 820 442 677 658 643 472 3712 Row 4 1095 659 982 907 895 627 5165 Row 5 787 403 670 671 613 476 3620 Total 2987 1641 2548 2406 2360 1718 13660
I'm assuming the second column top row is zero, although that makes the total not divisible by 3. Have there always been three Daily Doubles per game?
Quote:The average total per column is 2276.666667. If we do a chi-squared test of that average against the actual totals we get a value of 578.94 with 5 degrees of freedom. That probability of results that skewed are 1 in 1.39 * 10^122. That is like rolling 97.3 yo's in a row.
Any thoughts on why they favor certain columns and avoid others?
Quote: tringlomaneI wonder why the producers hate the 2nd and last category so much.
The only thing I can think of is that they often get 'cute' with the category in the last column; so, maybe they don't want the DD to be in a 'cute' category. I have no idea why they hate column 2 so much!
"Dealer has 'rock'... Pay 'paper!'"
May 30th, 2019 at 8:52:30 AM
permalink
My guess is that it is easier to fix a camera on certain squares so that when a player selects it, the director can cut to the shot immediately.
Simplicity is the ultimate sophistication - Leonardo da Vinci
May 30th, 2019 at 9:06:37 AM
permalink
Quote: WizardAny thoughts on why they favor certain columns and avoid others?
My first thought is that the sillier categories are on the right side, so Trebek can build to them as they are introduced. Might be a matter of avoiding the cute and possibly ambiguous clues as much as possible for the Daily Doubles.
Quote: WizardThat is like rolling 97.3 yo's in a row.
So you're saying it's possible
May 30th, 2019 at 9:28:58 AM
permalink
Good comments, thanks. So good that I can't think of anything worthwhile to add.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 30th, 2019 at 11:08:52 AM
permalink
I think if you go negative, you should be eliminated.
The older I get, the better I recall things that never happened
May 30th, 2019 at 11:26:12 AM
permalink
Quote: billryanI think if you go negative, you should be eliminated.
At any point in the game? That will slow the game down early on and make it more boring. Heck the game could end early even.
May 30th, 2019 at 12:41:03 PM
permalink
Quote: WizardSorry to keep replying to myself, but here is a table with those numbers:
Daily Doubles Column 1 Column 2 Column 3 Column 4 Column 5 Column 6 Total Row 1 5 0 3 3 2 3 16 Row 2 280 137 216 167 207 140 1147 Row 3 820 442 677 658 643 472 3712 Row 4 1095 659 982 907 895 627 5165 Row 5 787 403 670 671 613 476 3620 Total 2987 1641 2548 2406 2360 1718 13660
I'm assuming the second column top row is zero, although that makes the total not divisible by 3. Have there always been three Daily Doubles per game?
The average total per column is 2276.666667. If we do a chi-squared test of that average against the actual totals we get a value of 578.94 with 5 degrees of freedom. That probability of results that skewed are 1 in 1.39 * 10^122. That is like rolling 97.3 yo's in a row.
Any thoughts on why they favor certain columns and avoid others?
There have been games where all the Daily Doubles haven't been revealed. The incomplete data is causing the total to be off, but could it also be contributing to a bias in the observations?
Simplicity is the ultimate sophistication - Leonardo da Vinci
May 30th, 2019 at 12:46:50 PM
permalink
Quote: billryanI think if you go negative, you should be eliminated.
I would love to see a game show which changes a rule every week.
Sanitized for Your Protection
May 30th, 2019 at 12:48:41 PM
permalink
Quote: rxwineI would love to see a game show which changes a rule every week.
Isn't that "Survivor"?
Simplicity is the ultimate sophistication - Leonardo da Vinci
May 30th, 2019 at 1:00:14 PM
permalink
What happens if all 3 contestants end negative? What about ties (negative or positive)?
May 30th, 2019 at 1:06:45 PM
permalink
Maybe do it with two cuts? If you're negative after Jeopardy, you're out. And, if you're negative after double Jeopardy, you're out then. That might spice up the last part of the first round in some games. That part of the game can be kind of boring now, especially if the one DD comes out early.
"So as the clock ticked and the day passed, opportunity met preparation, and luck happened." - Maurice Clarett
May 30th, 2019 at 1:13:35 PM
permalink
Quote: rdw4potusMaybe do it with two cuts? If you're negative after Jeopardy, you're out. And, if you're negative after double Jeopardy, you're out then. That might spice up the last part of the first round in some games. That part of the game can be kind of boring now, especially if the one DD comes out early.
They could just shoot someone randomly. It would really spice things up.
Sanitized for Your Protection
May 30th, 2019 at 1:14:56 PM
permalink
Oops, sorry, didn't mean to spoil what will happen on game shows in our dystopian future.
Sanitized for Your Protection
May 30th, 2019 at 1:18:41 PM
permalink
Quote: rdw4potusMaybe do it with two cuts? If you're negative after Jeopardy, you're out. And, if you're negative after double Jeopardy, you're out then. That might spice up the last part of the first round in some games. That part of the game can be kind of boring now, especially if the one DD comes out early.
What would happen if 2 people are negative after the first round ?
May 30th, 2019 at 1:26:46 PM
permalink
According to Wikipedia (see the last paragraph in the "First Two Rounds" section), this happened once in the Art Fleming era. All 3 lost and there was no FJ.Quote: RSWhat happens if all 3 contestants end negative? What about ties (negative or positive)?
"Dealer has 'rock'... Pay 'paper!'"
May 30th, 2019 at 2:26:31 PM
permalink
Quote: JoemanAccording to Wikipedia (see the last paragraph in the "First Two Rounds" section), this happened once in the Art Fleming era. All 3 lost and there was no FJ.
And then they get an invoice in the mail?
A flute with no holes is not a flute, a donut with no holes is a danish
May 30th, 2019 at 2:38:44 PM
permalink
Quote: AyecarumbaQuote: WizardSorry to keep replying to myself, but here is a table with those numbers:
Daily Doubles Column 1 Column 2 Column 3 Column 4 Column 5 Column 6 Total Row 1 5 0 3 3 2 3 16 Row 2 280 137 216 167 207 140 1147 Row 3 820 442 677 658 643 472 3712 Row 4 1095 659 982 907 895 627 5165 Row 5 787 403 670 671 613 476 3620 Total 2987 1641 2548 2406 2360 1718 13660
I'm assuming the second column top row is zero, although that makes the total not divisible by 3. Have there always been three Daily Doubles per game?
The average total per column is 2276.666667. If we do a chi-squared test of that average against the actual totals we get a value of 578.94 with 5 degrees of freedom. That probability of results that skewed are 1 in 1.39 * 10^122. That is like rolling 97.3 yo's in a row.
Any thoughts on why they favor certain columns and avoid others?
There have been games where all the Daily Doubles haven't been revealed. The incomplete data is causing the total to be off, but could it also be contributing to a bias in the observations?
Yeah occasionally not all DDs are revealed. But significant observation bias, nah. Daily doubles are almost always revealed. I don't think any DDs have not been revealed since James has been on the show.
May 30th, 2019 at 3:03:09 PM
permalink
Quote: rxwineI would love to see a game show which changes a rule every week.
I'd watch a Showcase Showdown with American Ninja Warrior rules. Up the Mountain Climber, swing to Plinko, ride the Big Wheel...
The opinions of this moderator are for entertainment purposes only.
May 30th, 2019 at 9:49:05 PM
permalink
"Dates" is a WEAK category for him!! Very surprising given a lot of his wagers are based on dates! E.g. "Vegas Strong $10,117" and "Go Knights Go $10,617"
He didn't know a few of the clues in that category today. And only bet $5k on an $800 value DD question. I got 4 of 5, I missed the $2000 question (year of Queen Elizabeth I's death) by one year.
He didn't know a few of the clues in that category today. And only bet $5k on an $800 value DD question. I got 4 of 5, I missed the $2000 question (year of Queen Elizabeth I's death) by one year.
June 2nd, 2019 at 10:30:02 AM
permalink
You may wish to check your local listings for the times Jeopardy will air next week in your area.
For me here in Southern California, on...
...Wednesday the 5th it will air at 2:06 am Thursday morning, which is seven hours later than it normally does.
...Friday the 7th it will air at 2:06 am Saturday morning, again, seven hours later.
Your schedule may also be different, due to the NBA Playoffs.
For me here in Southern California, on...
...Wednesday the 5th it will air at 2:06 am Thursday morning, which is seven hours later than it normally does.
...Friday the 7th it will air at 2:06 am Saturday morning, again, seven hours later.
Your schedule may also be different, due to the NBA Playoffs.
June 2nd, 2019 at 10:34:02 AM
permalink
June 2nd, 2019 at 10:46:27 AM
permalink
Fortunately here in Chicago it airs at 3:30 in the afternoon
A flute with no holes is not a flute, a donut with no holes is a danish
June 2nd, 2019 at 10:55:00 AM
permalink
With the time difference, you will see Wednesday's show and Friday's show almost 13 hours before I will! :)Quote: Gabes22Fortunately here in Chicago it airs at 3:30 in the afternoon
I will have to remember to stay away from all social media those two nights, assuming I'd like to watch the show without knowing the result ahead of time, which would be my preference.
June 2nd, 2019 at 6:28:29 PM
permalink
Monday June 3rd - the show should be interesting.
If'n I'd a knowed you wanted to have went with me - I'd a seen that you got to get to go.
June 2nd, 2019 at 6:33:30 PM
permalink
Quote: PuckerbuttMonday June 3rd - the show should be interesting.
Have you seen it already?
Expect the worst and you will never be disappointed.
I AM NOT PART OF GWAE RADIO SHOW
June 2nd, 2019 at 6:34:30 PM
permalink
NoQuote: GWAEHave you seen it already?
If'n I'd a knowed you wanted to have went with me - I'd a seen that you got to get to go.
June 2nd, 2019 at 6:37:09 PM
permalink
Quote: PuckerbuttNo
Did you see results? Trying to figure out why it would be interesting. Because he can break record?
Expect the worst and you will never be disappointed.
I AM NOT PART OF GWAE RADIO SHOW
June 2nd, 2019 at 8:04:01 PM
permalink
I wonder if they will wheel out Ken Jennings to congratulate him when he breaks the record.
June 2nd, 2019 at 9:26:01 PM
permalink
Looks like James lost. It's over.
Last edited by: beachbumbabs on Jun 2, 2019
I tell you it’s wonderful to be here, man. I don’t give a damn who wins or loses. It’s just wonderful to be here with you people.
https://wizardofvegas.com/forum/gambling/betting-systems/33908-the-adventures-of-mdawg/
June 2nd, 2019 at 9:30:43 PM
permalink
Just an FYI....some douchebag at Sony has leaked future James episodes online.
Avoid the Internet or newspapers as it is all over the news right now. Very disappointing that someone would do this. Obviously an inside production job as its a main camera view.
Avoid the Internet or newspapers as it is all over the news right now. Very disappointing that someone would do this. Obviously an inside production job as its a main camera view.
June 2nd, 2019 at 9:49:29 PM
permalink
Is it confirmed that this episode is Monday’s? I couldn’t see anything on the clip I saw to confirm that.
June 2nd, 2019 at 10:03:43 PM
permalink
Quote: AussieIs it confirmed that this episode is Monday’s? I couldn’t see anything on the clip I saw to confirm that.
the viral clips and posts claim it is the next show. Sony has been removing the clips as fast as they can find them, so no confirmation.]
If the House lost every hand, they wouldn't deal the game.
June 2nd, 2019 at 10:46:23 PM
permalink
Just watched the clip on Twitter. People are speculating he lost on purpose because of his low final Jeopardy wager(??). I’m not buying that.
It was a fun ride to watch. Will be interesting to watch the whole episode to see what went wrong. I’m on vacation so I won’t see it till later in the week.
It was a fun ride to watch. Will be interesting to watch the whole episode to see what went wrong. I’m on vacation so I won’t see it till later in the week.
Ding Dong the Witch is Dead
June 2nd, 2019 at 10:50:25 PM
permalink
Given that everyone is using spoiler tags, it's pretty obvious what happened.
June 2nd, 2019 at 10:56:01 PM
permalink
Quote: RigondeauxGiven that everyone is using spoiler tags, it's pretty obvious what happened.
That and spoiler tags hide nothing on the front page.
Have you tried 22 tonight? I said 22.
June 2nd, 2019 at 11:11:57 PM
permalink
Quote: ams288Just watched the clip on Twitter. People are speculating he lost on purpose because of his low final Jeopardy wager(??). I’m not buying that.
It was a fun ride to watch. Will be interesting to watch the whole episode to see what went wrong. I’m on vacation so I won’t see it till later in the week.
Even betting it all he still loses based on totals prior to final jeopardy. The small bet was to guarantee a win in the event that the leader answered incorrectly.
June 2nd, 2019 at 11:49:16 PM
permalink
I would think heads are going to roll over a breach/leak like this. There's no question this wasn't an audience member filming. It came from their feed. In any event, if true, he lost in a manner that I thought would never happen...trailing going into final jeopardy
