Quote: WizardIt's time to remind the forum what the question at hand is. Here is the exact wording.
You have two dice in a shaker. You ask a friend to shake the dice and peek at the outcome, which he does. You ask him, "Is at least one of the dice a two?" He says, "Yes." What is the probability both dice are a two?
source
link to original post
I took the exact wording from the original post. But I can accept your wording because my point has always been that it's the wording that is the problem.
Here is the original wording from the first post:
You have two 6-sided dice in a cup. You shake the dice, and slam the cup down onto the table, hiding the result. Your partner peeks under the cup, and tells you, truthfully, "At least one of the dice is a 2."
What is the probability that both dice are showing a 2?
Quote: DieterI am increasingly unconvinced that the original question was not a personality test to see which assumptions people might favor.
link to original post
Yikes. Could you diagram that sentence for me? I admit I'm lost.
Quote: billryanI haven't figured out exactly how yet, but I plan on incorporating this question into my future hiring methods. Anyone who continues to insist it is 1/6 will eliminate themselves from the competition. I do love the hoops they will jump through arguing a 7th-grade math problem. It is one of the better exercises in logic I've come across.
link to original post
I'd love to see your report on the answers given.
Quote: AlanMendelsonQuote: billryanI haven't figured out exactly how yet, but I plan on incorporating this question into my future hiring methods. Anyone who continues to insist it is 1/6 will eliminate themselves from the competition. I do love the hoops they will jump through arguing a 7th-grade math problem. It is one of the better exercises in logic I've come across.
link to original post
I'd love to see your report on the answers given.
link to original post
Why? You'd read it and then ask how a six-sided die can result in a one in eleven chance. After fifty pages of your posts, what could possibly be in my report that might change your mind?
Everyone has said this is the way to answer it but no one has said why its the way.
Why would I look at 36 possible combinations of two dice when one die is known in a two dice problem?
How many times have I asked that?
Where does the question ask you to consider all of the combinations of dice with a 2?
How many times have I asked that?
Over the centuries our language has become simpler. Go read some document from the 1500s or just look at Lincoln's Gettysburg Address:
Four score and seven years ago our fathers brought forth on this continent, a new nation, conceived in Liberty, and dedicated to the proposition that all men are created equal.
Today it would be...
87 years ago this country was created with Liberty and equal rights for everybody.
Edited to add:
Back in the 1960s there was a magnificent CONFUSING book written by Marshall McCluhan called Understanding Media. You won't read it, I know. But a subtitle was The Medium Is The Message. I spent a full academic year studying that book and analyzing it for a course. My analysis was longer than the book and I interviewed everyone from Cousin Brucie on WABC to English professors to do it.
And so it is with the 2 dice question. It's the message.
Quote: AlanMendelsonQuote: DieterI am increasingly unconvinced that the original question was not a personality test to see which assumptions people might favor.
link to original post
Yikes. Could you diagram that sentence for me? I admit I'm lost.
link to original post
No. Sentence diagramming had fallen out of favor well before I went through school.
I got as far as "I" is the subject and "am" is a verb.
Quote: DieterQuote: AlanMendelsonQuote: DieterI am increasingly unconvinced that the original question was not a personality test to see which assumptions people might favor.
link to original post
Yikes. Could you diagram that sentence for me? I admit I'm lost.
link to original post
No. Sentence diagramming had fallen out of favor well before I went through school.
I got as far as "I" is the subject and "am" is a verb.
link to original post
LOL
Quote: WizardIt's time to remind the forum what the question at hand is. Here is the exact wording.
You have two dice in a shaker. You ask a friend to shake the dice and peek at the outcome, which he does. You ask him, "Is at least one of the dice a two?" He says, "Yes." What is the probability both dice are a two?
source
link to original post
Alan I didn�t read your post. And you didn�t read the quotes question. It�s about two dice. And you can easily recreate the experiment.
Quote: AlanMendelsonQuote: TravisRQuote: AlanMendelsonTravis it's 1/6.
You know it. I know it. There are others who know it but they don't want to be called... well never mind.
link to original post
A little further back in the discussion I saw where the situation unfolded slightly differently.... It said You ask the guy who just finished shaking the dice if there is at least one 2 and he says "Yes"..... I think at that point the odds of it being double 2's is 1:11.... becuase you've taken away the versions where he rolls something like 2-5 and instead of having any chance to call out a 5.... all 11 rolls now come into possibility equally......
I saw you had origianlly said 1 in 6 for this set-up as well and I'm wondering if you still think 1 in6?
link to original post
Pick up a pair of dice. Any dice.
Set at least one of the dice to show a 2.
Ask yourself: what are the odds both of the dice are 2s?
What would you do?
What I would do is pick up one die and count the faces. I would see six. One of the six is a 2. I would say 1/6.
Now this is NOT the actual question in the original problem. But this is the simple interpretation of the original question.
The original question uses additional words and conditions to make it more complicated.
But no where does the original question ask you to consider that there are 36 combinations of two dice and of those 36 combinations there are 11 combinations showing at least one two, and of those 11 combinations one combination shows 2-2.
Now I'm going to ask you:
I'm looking at two dice. One of the two dice is a two. But maybe both dice are 2s. But let's just start with one die as a 2. What are the odds that I'm looking at 2-2?
What are you visualizing in your mind from that question?
Are you visualizing in your mind 36 combinations of dice? Or are you visualizing two dice, one of which is a 2?
And here is the exact question again:
"You have two 6-sided dice in a cup. You shake the dice, and slam the cup down onto the table, hiding the result. Your partner peeks under the cup, and tells you, truthfully, "At least one of the dice is a 2."
What is the probability that both dice are showing a 2?"
Now I'll ask you what I asked before. Are you visualizing in your mind two dice or 36 combinations of two dice?
Final question. If by chance you are visualizing 36 combinations of two dice WHY are you visualizing 36 combinations? What words in the question asked you to visualize 36 combinations?
Because some math teacher said there are 11 combinations with at least one 2?
Or do you visualize two dice because the question tells you to visualize two dice?
link to original post
Hi there.
What I visualize is not the 36 combinations or permutations (I always mix those words up) of the 2 dice.... I wouldn't even say I visualize the 11 rolls that all have a "2" in them.....but in my mind I see one die showing a 2 and I see basically what would be a blank die, or something representing a die in my mind's eye, but all the sides are blank if that makes sense.... I can't even say I visualize a blank die it's more just like the word "DIE" ..... but lets call it a blank die for now.
At some point I do go back to thinking about the 36 possible rolls and imagine how they would all play out.... I've done so many probability problems in my life that dice and coins and whatever else that thinking about combinations is almost automatic.
And I think it provides a good way to check an answer. I can't say I came up with 1 out of 6 simply because the other die has 6 faces.....
THe first thing that made me realize it's probably one out of 6 is that you roll doubles 1 out of 6 times and that if the game is played over and over how could it be anything but 1 out of 6.
Then I went to figure out what was happening with the 11 rolls that have a 2 in them, and after a little thought I realized 5 of the rolls never make it to the part where a "2" is called out because it's the other number that's being called out. (assuming there is a 50% chance for each die that it is the one he calls out.... an assumption that I think is as valid as assuming the dice are perfectly fair)
I hope I answered your question ?
Quote: TravisRQuote: AlanMendelsonQuote: TravisRQuote: AlanMendelsonTravis it's 1/6.
You know it. I know it. There are others who know it but they don't want to be called... well never mind.
link to original post
A little further back in the discussion I saw where the situation unfolded slightly differently.... It said You ask the guy who just finished shaking the dice if there is at least one 2 and he says "Yes"..... I think at that point the odds of it being double 2's is 1:11.... becuase you've taken away the versions where he rolls something like 2-5 and instead of having any chance to call out a 5.... all 11 rolls now come into possibility equally......
I saw you had origianlly said 1 in 6 for this set-up as well and I'm wondering if you still think 1 in6?
link to original post
Pick up a pair of dice. Any dice.
Set at least one of the dice to show a 2.
Ask yourself: what are the odds both of the dice are 2s?
What would you do?
What I would do is pick up one die and count the faces. I would see six. One of the six is a 2. I would say 1/6.
Now this is NOT the actual question in the original problem. But this is the simple interpretation of the original question.
The original question uses additional words and conditions to make it more complicated.
But no where does the original question ask you to consider that there are 36 combinations of two dice and of those 36 combinations there are 11 combinations showing at least one two, and of those 11 combinations one combination shows 2-2.
Now I'm going to ask you:
I'm looking at two dice. One of the two dice is a two. But maybe both dice are 2s. But let's just start with one die as a 2. What are the odds that I'm looking at 2-2?
What are you visualizing in your mind from that question?
Are you visualizing in your mind 36 combinations of dice? Or are you visualizing two dice, one of which is a 2?
And here is the exact question again:
"You have two 6-sided dice in a cup. You shake the dice, and slam the cup down onto the table, hiding the result. Your partner peeks under the cup, and tells you, truthfully, "At least one of the dice is a 2."
What is the probability that both dice are showing a 2?"
Now I'll ask you what I asked before. Are you visualizing in your mind two dice or 36 combinations of two dice?
Final question. If by chance you are visualizing 36 combinations of two dice WHY are you visualizing 36 combinations? What words in the question asked you to visualize 36 combinations?
Because some math teacher said there are 11 combinations with at least one 2?
Or do you visualize two dice because the question tells you to visualize two dice?
link to original post
Hi there.
What I visualize is not the 36 combinations or permutations (I always mix those words up) of the 2 dice.... I wouldn't even say I visualize the 11 rolls that all have a "2" in them.....but in my mind I see one die showing a 2 and I see basically what would be a blank die, or something representing a die in my mind's eye, but all the sides are blank if that makes sense.... I can't even say I visualize a blank die it's more just like the word "DIE" ..... but lets call it a blank die for now.
At some point I do go back to thinking about the 36 possible rolls and imagine how they would all play out.... I've done so many probability problems in my life that dice and coins and whatever else that thinking about combinations is almost automatic.
And I think it provides a good way to check an answer. I can't say I came up with 1 out of 6 simply because the other die has 6 faces.....
THe first thing that made me realize it's probably one out of 6 is that you roll doubles 1 out of 6 times and that if the game is played over and over how could it be anything but 1 out of 6.
Then I went to figure out what was happening with the 11 rolls that have a 2 in them, and after a little thought I realized 5 of the rolls never make it to the part where a "2" is called out because it's the other number that's being called out. (assuming there is a 50% chance for each die that it is the one he calls out.... an assumption that I think is as valid as assuming the dice are perfectly fair)
I hope I answered your question ?
link to original post
What are you talking about? That isn't part of anything. The person isn't calling out the results of the roll. He is letting you know the roll contained two. If there are no twos, he doesn't call out there is a five.
Quote: billryanWhat are you talking about? That isn't part of anything. The person isn't calling out the results of the roll. He is letting you know the roll contained two. If there are no twos, he doesn't call out there is a five.
link to original post
I don't know that we know that.
edit: ... depending on which of at least five versions of the question are being considered.
Because you don't know which of the two dies is known. And that is what makes all the difference in the world.Quote: AlanMendelsonBill, an actual answer could change my mind.
Everyone has said this is the way to answer it but no one has said why its the way.
Why would I look at 36 possible combinations of two dice when one die is known in a two dice problem?
When you don't know which of the two dies is known, you have this as your possible dice throws:

That's why it's still a "two dice" problem. A roll if 2-1 is a different roll than a roll of 1-2. A roll of 5-4 is a different roll than 4-5.
However, if you say the left die is a 2 or the red die is a 2, etc., then you DO know which of the two dies is known, and THEN it can be considered a one die problem, and the answer is 1/6.

Well... the question doesn't "ask you to consider it" specifically, in the same way that when I ask, What's the largest state in the union? I'm not specifically asking you to consider Alaska and Hawaii. But you need to do so, to answer that question correctly.Quote: AlanMendelsonWhere does the question ask you to consider all of the combinations of dice with a 2?
It's up to the reader to arrive at the correct probability, and considering all of the combinations of how two dice can be thrown will help to arrive at the correct answer.
Quote: DieterQuote: billryanWhat are you talking about? That isn't part of anything. The person isn't calling out the results of the roll. He is letting you know the roll contained two. If there are no twos, he doesn't call out there is a five.
link to original post
I don't know that we know that.
link to original post
I believe we do. We certainly know that any roll involving a two will be told it has a two in it, regardless of any other number. We can certainly infer he isn't calling out what is on either dice every roll or it negates the whole exercise.
Man calls out there is at least one two, and we have an exercise.
Man calls out we have a 2 and a 5, Under those conditions, I think anyone here would say the chances of there being a pair of 2s is pretty slim.
I'm gonna repeat my final conclusion.Quote: WizardIt's time to remind the forum what the question at hand is. Here is the exact wording.
You have two dice in a shaker. You ask a friend to shake the dice and peek at the outcome, which he does. You ask him, "Is at least one of the dice a two?" He says, "Yes." What is the probability both dice are a two?
source
link to original post
Alan is right. Wording is important.
That said, Alan is wrong that the wording difficulty automatically makes the answer 1/6.
The answer, based on the question as quoted by the Wizard above, is 1/11.
The answer, based on the re-wording that Alan seems to refer to, could be either 1/11 or 1/6.
It really depends on the parameters of the person peeking and reporting.
If he is forced to state either "There is at least one 2" or "There are no 2s" then there is a 1/11 chance the other die is a 2, when at least one is a 2.
If, however, he says "There is at least one 2" or "There is at least one 3" or "There is at least one 4" or "There is at least one 5" or "There is at least one 6" or "There is at least one 1" but never reports the absence of a potential result (ie never says "There are no 2s" etc) then the chance the other die matches the reported value is 1/6.
I'm sorry, but you need to explain this. "If he says there are no 2s then there is a 1/11 chance the other die is a two?"
Oops. I fixed my post to say:Quote: billryan"If he is forced to state either "There is at least one 2" or "There are no 2s" then there is a 1/11 chance the other die is a 2."
I'm sorry, but you need to explain this. "If he says there are no 2s then there is a 1/11 chance the other die is a two?"
link to original post
� there is a 1/11 chance, when there�s at least one 2.
Yeah, Alan is right. The wording can bite you in the ass!
Quote: billryanQuote: DieterQuote: billryanWhat are you talking about? That isn't part of anything. The person isn't calling out the results of the roll. He is letting you know the roll contained two. If there are no twos, he doesn't call out there is a five.
link to original post
I don't know that we know that.
link to original post
I believe we do. We certainly know that any roll involving a two will be told it has a two in it, regardless of any other number. We can certainly infer he isn't calling out what is on either dice every roll or it negates the whole exercise.
Man calls out there is at least one two, and we have an exercise.
Man calls out we have a 2 and a 5, Under those conditions, I think anyone here would say the chances of there being a pair of 2s is pretty slim.
link to original post
If I ask "Are there any 2's?", the answer could be "There is at least one 2." or something like "Go fish!*"
If I don't ask, and there is no prior agreement, how do I know what else I know when my dice inspector peeks the hole dice and reports "There is at least one 2."
*: I have no pecuniary interest in this link.
Quote: TravisR
And I think it provides a good way to check an answer. I can't say I came up with 1 out of 6 simply because the other die has 6 faces.....
THe first thing that made me realize it's probably one out of 6 is that you roll doubles 1 out of 6 times and that if the game is played over and over how could it be anything but 1 out of 6.
Then I went to figure out what was happening with the 11 rolls that have a 2 in them, and after a little thought I realized 5 of the rolls never make it to the part where a "2" is called out because it's the other number that's being called out. (assuming there is a 50% chance for each die that it is the one he calls out.... an assumption that I think is as valid as assuming the dice are perfectly fair)
I hope I answered your question ?
link to original post
Truncated quote.
You are thinking about it correctly. But 1/6 is just the chance of rolling a double. The rules that the person calling the numbers follows will still alter the chance of a particular double being there given the caller said something.
Here�s an example. Assume the caller rules are as follows:
1) If there�s at least one 1, say �there is at least one 1.�
2) If there are no 1s but at least one 2, say �there is at least one 2.�
3) So on* for 3, 4, 5 and 6.
[Edit of obvious typo]
Now if the caller says �there is at least one 6� you know the probability of two 6s is 100%. Because the caller only says that statement if he doesn�t see any lower numbers.
Similarly, if the caller says �there is at least one 1� you know the probability of a double 1 to be 1/11.
You can work out the rest. It goes 2: 1/9. 3: 1/7. 4: 1/5. 5: 1/3.
On average a double is still rolled 1/6 times. But the new info given by what the speaker says will impact the probabilities that any particular one was rolled. It�s Bayes theorem at that point.
You have two 6-sided dice in a cup. You shake the dice, and slam the cup down onto the table, hiding the result. Your partner peeks under the cup, and tells you, truthfully, "At least one of the dice is a 2."
What is the probability that both dice are showing a 2?
Quote: DJTeddyBearI'm gonna repeat my final conclusion.Quote: WizardIt's time to remind the forum what the question at hand is. Here is the exact wording.
You have two dice in a shaker. You ask a friend to shake the dice and peek at the outcome, which he does. You ask him, "Is at least one of the dice a two?" He says, "Yes." What is the probability both dice are a two?
source
link to original post
Alan is right. Wording is important.
That said, Alan is wrong that the wording difficulty automatically makes the answer 1/6.
The answer, based on the question as quoted by the Wizard above, is 1/11.
The answer, based on the re-wording that Alan seems to refer to, could be either 1/11 or 1/6.
It really depends on the parameters of the person peeking and reporting.
If he is forced to state either "There is at least one 2" or "There are no 2s" then there is a 1/11 chance the other die is a 2, when at least one is a 2.
If, however, he says "There is at least one 2" or "There is at least one 3" or "There is at least one 4" or "There is at least one 5" or "There is at least one 6" or "There is at least one 1" but never reports the absence of a potential result (ie never says "There are no 2s" etc) then the chance the other die matches the reported value is 1/6.
link to original post
Okay, for the problem as it is stated above (where you ask if there is a "2" and the answer is yes) I can agree with 1 out of 11 being the answer
And I also agree that for the problem where the guy looks under the cup and announces there is a "2": that the answer for the question on chances of it being double 2's at that point is 1 out of 6.
The cause of the difference I'm also pretty sure I agree with.... for the former situation, you are informed every time at least one 2 comes up..... in the latter situation, you can't assume that EVERY time a 2 is present that you will be informed of that. So the 11 possibilites are basically not all represented evenly.....i.e. half the time if there is only one 2 , you won't be told there is a 2..... you will be told whatever the other number is (That is an assumption I suppose, but it's no more of an assumption than assuming the dice are fair and balanced)
Thank you
Quote: unJonQuote: TravisR
And I think it provides a good way to check an answer. I can't say I came up with 1 out of 6 simply because the other die has 6 faces.....
THe first thing that made me realize it's probably one out of 6 is that you roll doubles 1 out of 6 times and that if the game is played over and over how could it be anything but 1 out of 6.
Then I went to figure out what was happening with the 11 rolls that have a 2 in them, and after a little thought I realized 5 of the rolls never make it to the part where a "2" is called out because it's the other number that's being called out. (assuming there is a 50% chance for each die that it is the one he calls out.... an assumption that I think is as valid as assuming the dice are perfectly fair)
I hope I answered your question ?
link to original post
Truncated quote.
You are thinking about it correctly. But 1/6 is just the chance of rolling a double. The rules that the person calling the numbers follows will still alter the chance of a particular double being there given the caller said something.
Here�s an example. Assume the caller rules are as follows:
1) If there�s at least one 1, say �there is at least one 1.�
2) If there are no 1s but at least one 2, say �there is at least one 2.�
3) So on* for 3, 4, 5 and 6.
[Edit of obvious typo]
Now if the caller says �there is at least one 6� you know the probability of two 6s is 100%. Because the caller only says that statement if he doesn�t see any lower numbers.
Similarly, if the caller says �there is at least one 1� you know the probability of a double 1 to be 1/11.
You can work out the rest. It goes 2: 1/9. 3: 1/7. 4: 1/5. 5: 1/3.
On average a double is still rolled 1/6 times. But the new info given by what the speaker says will impact the probabilities that any particular one was rolled. It�s Bayes theorem at that point.
link to original post
I think I can agree with everything here.... of course any rules for the speaker will most likely affect the answer. Most things should not be assumed. Weather or not the assumption that the caller is calling out a die at random from the two he sees isn't explicitly stated in the problem.... but there is no reason to think it isn't random.... this particular assumption could be debated , but in the end I think the 50/50 assumption is a reasonable, almost-goes-without-saying assumption. You wouldn't assume the guy has a phobia of other numbers..... you would assume he's a normal well-adjusted man with no real bias toward anything, lol"
Thank you
After all the deliberation that�s already happened in this thread as well as my prior response, it should not surprise you to see that my response is, I need more information. Specifically, why did he report about 2s?Quote: AlanMendelsonDJ Teddy Bear, here is the ORIGINAL question as it appeared the VERY FIRST TIME on this forum. Please give your answer to this exact wording:
You have two 6-sided dice in a cup. You shake the dice, and slam the cup down onto the table, hiding the result. Your partner peeks under the cup, and tells you, truthfully, "At least one of the dice is a 2."
What is the probability that both dice are showing a 2?
link to original post
If he was, for whatever reason, only reporting on 2s, then the odds are 1/11.
If he was always merely telling you the value of either die, then it�s 1/6.
Again, as worded, it�s not a math problem but an English comprehension problem.
Of course, there is another option.
If this question were on a college level probability / statistics test, would it be safe to assume that the obvious answer of 1/6 must be wrong?
Quote: DJTeddyBearAfter all the deliberation that�s already happened in this thread as well as my prior response, it should not surprise you to see that my response is, I need more information. Specifically, why did he report about 2s?Quote: AlanMendelsonDJ Teddy Bear, here is the ORIGINAL question as it appeared the VERY FIRST TIME on this forum. Please give your answer to this exact wording:
You have two 6-sided dice in a cup. You shake the dice, and slam the cup down onto the table, hiding the result. Your partner peeks under the cup, and tells you, truthfully, "At least one of the dice is a 2."
What is the probability that both dice are showing a 2?
link to original post
If he was, for whatever reason, only reporting on 2s, then the odds are 1/11.
If he was always merely telling you the value of either die, then it�s 1/6.
Again, as worded, it�s not a math problem but an English comprehension problem.
Of course, there is another option.
If this question were on a college level probability / statistics test, would it be safe to assume that the obvious answer of 1/6 must be wrong?
link to original post
My thoughts about this are:
If there is no information otherwise you would assume he just is telling you what at least one of the dice are. Why? Because that's what the problem says happened.
You don't need any more information to come to an answer, and if you did need more information, it should be given in the problem.
I didn't write the problem.... but if the intended answer was 1/11, they didn't word the problem correctly.
You can get to an answer of 1/6 by assuming that the problem isn't withholding information from you and that it was written correctly (which seems like was the assumption which didn't pan out to be true)
When I first saw this problem I thought 1/11 was the obvious answer, and only when I thought "It can't be that easy" did I look more carefully and realize it was 1 out of 6.
AS it turns out, mistake or not, it's probably one of the best probability problems I've ever seen (see what I did there, lol)
Thank you
Quote: unJonWith no further information I assume the caller of �at least one two� is trying to rope me into a Three Card Monte rigged game. So I assume the chance of the second 2 is either 100% or 0% depending on what bet he is offering me.
link to original post
I'm not sure "partner" would have been the word I used if that was the case, lol
Quote: AlanMendelsonQuote: DieterQuote: AlanMendelsonQuote: DieterI am increasingly unconvinced that the original question was not a personality test to see which assumptions people might favor.
link to original post
Yikes. Could you diagram that sentence for me? I admit I'm lost.
link to original post
No. Sentence diagramming had fallen out of favor well before I went through school.
I got as far as "I" is the subject and "am" is a verb.
link to original post
LOL
link to original post
Suppose you were interested in how people approach an unsolvable puzzle.
Would you perhaps post such a puzzle on a forum reasonably known for puzzle solvery, make popcorn, kick back, and watch the show for a while?
That's got to be years of entertainment data to analyze.
I'm not convinced it's not a personality test.
I've come up with another few answers over the last few hours, but they're out of context to the original.
Set at least one of the dice to show a 2.
Ask yourself: what are the odds both of the dice are 2s?
What would you do?
What I would do is pick up one die and count the faces. I would see six. One of the six is a 2. I would say 1/6.
**** Honestly I pick up the dice and at that point they aren't on a face, they are in my hand..... so I guess I could take one out and set it on the table showing a 2, but the other die is still valueless..... so in an attempt to finish this particular question , I would roll the die and say 1 out 6 chances it lands on a 2
Now this is NOT the actual question in the original problem. But this is the simple interpretation of the original question.
The original question uses additional words and conditions to make it more complicated.
But no where does the original question ask you to consider that there are 36 combinations of two dice and of those 36 combinations there are 11 combinations showing at least one two, and of those 11 combinations one combination shows 2-2.
***** I can agree with that
Now I'm going to ask you:
I'm looking at two dice. One of the two dice is a two. But maybe both dice are 2s. But let's just start with one die as a 2. What are the odds that I'm looking at 2-2?
What are you visualizing in your mind from that question?
***********In my mind I'm trying to figure out if you just finished rolling the dice or if you walked up to a table and saw two dice just sitting there. Not to be difficult but you didn't say anything about rolling or shaking any dice in this particular question
Are you visualizing in your mind 36 combinations of dice? Or are you visualizing two dice, one of which is a 2?
And here is the exact question again:
"You have two 6-sided dice in a cup. You shake the dice, and slam the cup down onto the table, hiding the result. Your partner peeks under the cup, and tells you, truthfully, "At least one of the dice is a 2."
What is the probability that both dice are showing a 2?"
Now I'll ask you what I asked before. Are you visualizing in your mind two dice or 36 combinations of two dice?
***** honestly in my mind at this point i'm visulizing an initial 36 combinations of dice and also a set of dice with one of them on 2
Final question. If by chance you are visualizing 36 combinations of two dice WHY are you visualizing 36 combinations? What words in the question asked you to visualize 36 combinations?
**** The part where he shakes the dice up and rolls to produce a random roll is what kicks the visuization of 36 off in my mind..... pretty much before I can even realizing I'm doing it
Because some math teacher said there are 11 combinations with at least one 2?
****** if by math teacher you mean myself than sure
Or do you visualize two dice because the question tells you to visualize two dice?
***** I also visulize two dice
link to original post
Quote: TravisRPick up a pair of dice. Any dice.
Set at least one of the dice to show a 2.
Ask yourself: what are the odds both of the dice are 2s?
What would you do?
What I would do is pick up one die and count the faces. I would see six. One of the six is a 2. I would say 1/6.
**** Honestly I pick up the dice and at that point they aren't on a face, they are in my hand..... so I guess I could take one out and set it on the table showing a 2, but the other die is still valueless..... so in an attempt to finish this particular question , I would roll the die and say 1 out 6 chances it lands on a 2
Now this is NOT the actual question in the original problem. But this is the simple interpretation of the original question.
The original question uses additional words and conditions to make it more complicated.
But no where does the original question ask you to consider that there are 36 combinations of two dice and of those 36 combinations there are 11 combinations showing at least one two, and of those 11 combinations one combination shows 2-2.
***** I can agree with that
Now I'm going to ask you:
I'm looking at two dice. One of the two dice is a two. But maybe both dice are 2s. But let's just start with one die as a 2. What are the odds that I'm looking at 2-2?
What are you visualizing in your mind from that question?
***********In my mind I'm trying to figure out if you just finished rolling the dice or if you walked up to a table and saw two dice just sitting there. Not to be difficult but you didn't say anything about rolling or shaking any dice in this particular question
Are you visualizing in your mind 36 combinations of dice? Or are you visualizing two dice, one of which is a 2?
And here is the exact question again:
"You have two 6-sided dice in a cup. You shake the dice, and slam the cup down onto the table, hiding the result. Your partner peeks under the cup, and tells you, truthfully, "At least one of the dice is a 2."
What is the probability that both dice are showing a 2?"
Now I'll ask you what I asked before. Are you visualizing in your mind two dice or 36 combinations of two dice?
***** honestly in my mind at this point i'm visulizing an initial 36 combinations of dice and also a set of dice with one of them on 2
Final question. If by chance you are visualizing 36 combinations of two dice WHY are you visualizing 36 combinations? What words in the question asked you to visualize 36 combinations?
**** The part where he shakes the dice up and rolls to produce a random roll is what kicks the visuization of 36 off in my mind..... pretty much before I can even realizing I'm doing it
Because some math teacher said there are 11 combinations with at least one 2?
****** if by math teacher you mean myself than sure
Or do you visualize two dice because the question tells you to visualize two dice?
***** I also visulize two dice
link to original post
link to original post
All the thinking and squinting doesn't change the math.
Giving an answer to a question no one asked means you didn't answer the question you were asked.
Quote: EdCollinsBecause you don't know which of the two dies is known. And that is what makes all the difference in the world.Quote: AlanMendelsonBill, an actual answer could change my mind.
Everyone has said this is the way to answer it but no one has said why its the way.
Why would I look at 36 possible combinations of two dice when one die is known in a two dice problem?
When you don't know which of the two dies is known, you have this as your possible dice throws:
That's why it's still a "two dice" problem. A roll if 2-1 is a different roll than a roll of 1-2. A roll of 5-4 is a different roll than 4-5.
However, if you say the left die is a 2 or the red die is a 2, etc., then you DO know which of the two dies is known, and THEN it can be considered a one die problem, and the answer is 1/6.Well... the question doesn't "ask you to consider it" specifically, in the same way that when I ask, What's the largest state in the union? I'm not specifically asking you to consider Alaska and Hawaii. But you need to do so, to answer that question correctly.Quote: AlanMendelsonWhere does the question ask you to consider all of the combinations of dice with a 2?
It's up to the reader to arrive at the correct probability, and considering all of the combinations of how two dice can be thrown will help to arrive at the correct answer.
link to original post
How about this situation:
The Wiz and I are playing this game:
Quote:Two dice are shaken. One die is red, the other white.
A third party examines the roll privately, and truthfully announces whenever there is at least one 2.
If there are zero twos, no money changes hands.
If there is one two, you pay me [the Wiz] whatever your wager is.
If there are two twos, then I pay you [LoquaciousMoFW] 8x your wager.
For whatever reason, I am down my initial loss limit of $200 and about to quit when the Wiz offers the following:
"Don't go! Keep playing and I'll agree to the following modification to give you the chance to get even: When there is a two, the peeker will announce the color of the die he first noticed a 2, red or white."
So, do I accept the offer or run away as fast as possible? Why?
The Wiz and I are playing this game:
Quote:Two dice are shaken. One die is red, the other white.
A third party examines the roll privately, and truthfully announces whenever there is at least one 2.
If there are zero twos, no money changes hands.
If there is one two, you pay me [the Wiz] whatever your wager is.
If there are two twos, then I pay you [LoquaciousMoFW] 8x your wager.
For whatever reason, I am down my initial loss limit of $200 and about to quit when the Wiz offers the following:
"Don't go! Keep playing and I'll agree to the following modification to give you the chance to get even: When there is a two, the peeker will announce the color of the die he first noticed a 2, red or white."
So, do I accept the offer or run away as fast as possible? Why?
link to original post
**** forgive me if I'm answering a question that wasn't asked.....
***** you are down $200 because you are getting paid 8 :1 on an 10:1 shot
**** I don't think it matters what color the dice are (That's the "why")..... Whether he says red or white I don't see how it matters..... so run away....
Quote: LoquaciousMoFWQuote: EdCollinsBecause you don't know which of the two dies is known. And that is what makes all the difference in the world.Quote: AlanMendelsonBill, an actual answer could change my mind.
Everyone has said this is the way to answer it but no one has said why its the way.
Why would I look at 36 possible combinations of two dice when one die is known in a two dice problem?
When you don't know which of the two dies is known, you have this as your possible dice throws:
That's why it's still a "two dice" problem. A roll if 2-1 is a different roll than a roll of 1-2. A roll of 5-4 is a different roll than 4-5.
***** This is where the road splits...... A 2-1 roll is different than a 1-2 roll..... that's why it comes up twice as much as a 2-2 roll. (Obviously)
***** That logic is solid
***** What's missing is how do you account for the times when a 2-1 is rolled and the guy announces a "1"?.... That right there is what makes it a little different than a "two-die" problem
However, if you say the left die is a 2 or the red die is a 2, etc., then you DO know which of the two dies is known, and THEN it can be considered a one die problem, and the answer is 1/6.
******* so if it's the red die thats a 2 it's 1/6
if it's the white die than it's 1/6
I want to go out on a limb and say if he doesn't tell us I'll just assume it's either on the RED of the WHITE and then consult the sentences I just wrote and say 1 out of 6
Well... the question doesn't "ask you to consider it" specifically, in the same way that when I ask, What's the largest state in the union? I'm not specifically asking you to consider Alaska and Hawaii. But you need to do so, to answer that question correctly.Quote: AlanMendelsonWhere does the question ask you to consider all of the combinations of dice with a 2?
It's up to the reader to arrive at the correct probability, and considering all of the combinations of how two dice can be thrown will help to arrive at the correct answer.
link to original post
How about this situation:
The Wiz and I are playing this game:Quote:Two dice are shaken. One die is red, the other white.
A third party examines the roll privately, and truthfully announces whenever there is at least one 2.
If there are zero twos, no money changes hands.
If there is one two, you pay me [the Wiz] whatever your wager is.
If there are two twos, then I pay you [LoquaciousMoFW] 8x your wager.
For whatever reason, I am down my initial loss limit of $200 and about to quit when the Wiz offers the following:
"Don't go! Keep playing and I'll agree to the following modification to give you the chance to get even: When there is a two, the peeker will announce the color of the die he first noticed a 2, red or white."
So, do I accept the offer or run away as fast as possible? Why?
link to original post
Quote: LoquaciousMoFWQuote: EdCollinsBecause you don't know which of the two dies is known. And that is what makes all the difference in the world.Quote: AlanMendelsonBill, an actual answer could change my mind.
Everyone has said this is the way to answer it but no one has said why its the way.
Why would I look at 36 possible combinations of two dice when one die is known in a two dice problem?
When you don't know which of the two dies is known, you have this as your possible dice throws:
That's why it's still a "two dice" problem. A roll if 2-1 is a different roll than a roll of 1-2. A roll of 5-4 is a different roll than 4-5.
However, if you say the left die is a 2 or the red die is a 2, etc., then you DO know which of the two dies is known, and THEN it can be considered a one die problem, and the answer is 1/6.Well... the question doesn't "ask you to consider it" specifically, in the same way that when I ask, What's the largest state in the union? I'm not specifically asking you to consider Alaska and Hawaii. But you need to do so, to answer that question correctly.Quote: AlanMendelsonWhere does the question ask you to consider all of the combinations of dice with a 2?
It's up to the reader to arrive at the correct probability, and considering all of the combinations of how two dice can be thrown will help to arrive at the correct answer.
link to original post
How about this situation:
The Wiz and I are playing this game:Quote:Two dice are shaken. One die is red, the other white.
A third party examines the roll privately, and truthfully announces whenever there is at least one 2.
If there are zero twos, no money changes hands.
If there is one two, you pay me [the Wiz] whatever your wager is.
If there are two twos, then I pay you [LoquaciousMoFW] 8x your wager.
For whatever reason, I am down my initial loss limit of $200 and about to quit when the Wiz offers the following:
"Don't go! Keep playing and I'll agree to the following modification to give you the chance to get even: When there is a two, the peeker will announce the color of the die he first noticed a 2, red or white."
So, do I accept the offer or run away as fast as possible? Why?
link to original post
Clever Wizard. Run! You�ve now made this truly a Monty Hall problem.
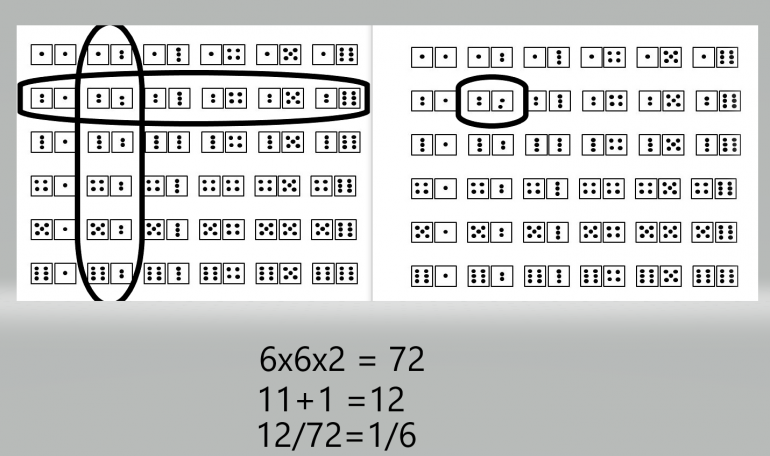
hopefully my graphic comes through better than my ability to stay focused.....
For the problem that has the two dice, and the partner who yells stuff out about some of what he sees....and to counter the 1:11 argument....
I saw this representation a lot of the 36 combinations and 11 of them circled like the left side of my picture.
What's missing from this way of looking at it is that there are really 72 different things that can happen if you take into account that there are 2 different dice that could be called out..... so it's not just 6x6 for total possibilities..... it's 6x6x2 = 72 different things that could happen
So the 11 rolls are all there, and then on the other chart you will see one more circled item being the 2-2 roll because there is no option on that roll, a "2" must be called.
So that's now 11+1=12.......... 12 out of 72. Ta da
It would probably be more "correct" to break it up into two group of 6 dice on both charts....but .... we are all pretty smart here ...... I think
If the caller only says �at least one two� every time there is at least one two, and says nothing the rest of the time, then it is 1/11.
If the caller will randomly pick one die and say whatever number is on that die, then it�s 1/6.
With different rules there are different probabilities.
In the absence of knowing the rules, there�s no necessarily correct answer. It�s �indeterminate� like zero divided by zero.
Quote: unJonTravisR you seem like a smart person. I don�t know why you are tilting at windmills here. The answer depends on the rules the caller follows. Without defining those rules, I can�t follow whether the answer is 1/11 or 1/6 or some other number.
If the caller only says �at least one two� every time there is at least one two, and says nothing the rest of the time, then it is 1/11.
If the caller will randomly pick one die and say whatever number is on that die, then it�s 1/6.
With different rules there are different probabilities.
In the absence of knowing the rules, there�s no necessarily correct answer. It�s �indeterminate� like zero divided by zero.
link to original post
Well..... I guess the way I look at it is that there are no "rules' for the caller to follow..... none were laid out, so it would seem to me that there simply aren't any rules he needs to follow. You can of course, add rules and get different results depending on what rules you add. But when I read the problem, and I don't add any rules to it and take it just as it was written.... I come up with 1 out of 6.
i.e. there is no rule that he has to call out the "left" die, or the "white die" or a "2" if there is other numbers available to call.
The only rule I held him to was that he was truthful.... but that was said in the problem so it's valid to assume that.
That's my current view of the problem anyhow.
Thank you
For me when I read the original problem, my response is that I don�t have enough information to calculate the probability.
Quote: unJonThank you. I think that�s why Dieter calls the original problem a personality test.
For me when I read the original problem, my response is that I don�t have enough information to calculate the probability.
link to original post
I can appreciate that....lol.... I think that thought flashed thru my mind too.
The funny thing is is that you have more information than if the guy said nothing at all.
Or even a step further back..... your partner shake some dice and slams them on the table..... well that's obviously 1 out of 6
Now we can say something like.... He slams the dice on the table and looks at them........ still 1 out of 6
Now we get to the part where he says something about them (there is at least one "2".... now that is a little bit of information, but like you said earlier, the question becomes "was what he said governed by any rules?"..... If there wasn't any rules governing what he said, it's not enough information to change the odds of there being doubles under the cup one way or the other because you can always announce at least one of something.
There's also something to be said about volunteering of information and it's usefulness.... what I mean by that is are you more impressed by someone who walks up to you and says (truthfully)...... I just rolled double 6's 10 consecutive times...... or someone who says "I bet I can roll double 6's ten times in a row" and then does it?
You'd probably be more impressed by the latter guy, even tho they both did the exact same thing.
Because the first guy "voulunteered" his situation..... so it doesn't mean nearly as much..... I think some of that applies to the guy saying he sees a "2".... it's like ..... so what?, lol
I'm rambling a little bit..... just fun stuff to think about
Thank you
Quote: unJonTravisR you seem like a smart person. I don�t know why you are tilting at windmills here. The answer depends on the rules the caller follows. Without defining those rules, I can�t follow whether the answer is 1/11 or 1/6 or some other number.
If the caller only says �at least one two� every time there is at least one two, and says nothing the rest of the time, then it is 1/11.
If the caller will randomly pick one die and say whatever number is on that die, then it�s 1/6.
With different rules there are different probabilities.
In the absence of knowing the rules, there�s no necessarily correct answer. It�s �indeterminate� like zero divided by zero.
link to original post
Yes. Thank you.
I agree that as originally worded, the correct answer was subject to interpretation. However, Wiz's rewording of the problem on page 7 of this thread eliminated these ambiguities:Quote: AlanMendelsonQuote: unJonTravisR you seem like a smart person. I don�t know why you are tilting at windmills here. The answer depends on the rules the caller follows. Without defining those rules, I can�t follow whether the answer is 1/11 or 1/6 or some other number.
If the caller only says �at least one two� every time there is at least one two, and says nothing the rest of the time, then it is 1/11.
If the caller will randomly pick one die and say whatever number is on that die, then it�s 1/6.
With different rules there are different probabilities.
In the absence of knowing the rules, there�s no necessarily correct answer. It�s �indeterminate� like zero divided by zero.
link to original post
Yes. Thank you.
link to original post
Quote: WizardQuote: New wordingYou have two dice in a shaker. You ask a friend to shake the dice and peek at the outcome, which he does. You ask him, "Is at least one of the dice a two?" He says, "Yes." What is the probability both dice are a two?
link to original post
Quote: AlanMendelsonYeah... except for years the argument was over the original wording and not the Wizards revised wording.
link to original post
Does it really matter if you still insist the probability is still 1/6 in the revised wording as well?
Quote: AlanMendelsonYeah... except for years the argument was over the original wording and not the Wizards revised wording.
link to original post
Well of course !....... the revised wording is no fun.....
I still think the original wording was fine though. I think absence of rules is different than ambiguity of rules.
Thank you
It is a Monte Carlo simulation of random rolls of two dice, counting the outcomes of "any 2", "both dice are 2", and "the first die is a 2".
SETUP
The setup for one line of base data is
-
* Random values 1 through 6 for "die1" and "die2" independently.
* "Any 2" is TRUE if "die1" (boolean) OR "die2" is 2.
* "Both are 2" is TRUE if "die1" (boolean) AND "die2" are 2.
* "The first is 2" is TRUE if "die1" equlas 2.
This data line is copied all way down to row 360001 giving 360000 independent dice rolls.
| die1 | die2 | any2? | both2? | first2? | fin |
|---|---|---|---|---|---|
| =INT(RAND()*6)+1 | =INT(RAND()*6)+1 | =OR(A2=2;B2=2) | =AND(A2=2;B2=2) | =A2=2 |

Counting and summing up is left to a Pivot Table:
-
* Counting the boolean results of "both dice are 2".
* The rows show the "any 2" case.
* The columns add the view of the "first die is 2" case.
Refreshing the Pivot Table varies the values and thus validates that dice rolls actually are simulated.
A second display references the Pivot Table and
-
* Normalizes the simulation values to 36.
* Rounds the values and avoids decimals.
* Stabilizes the simulation result.
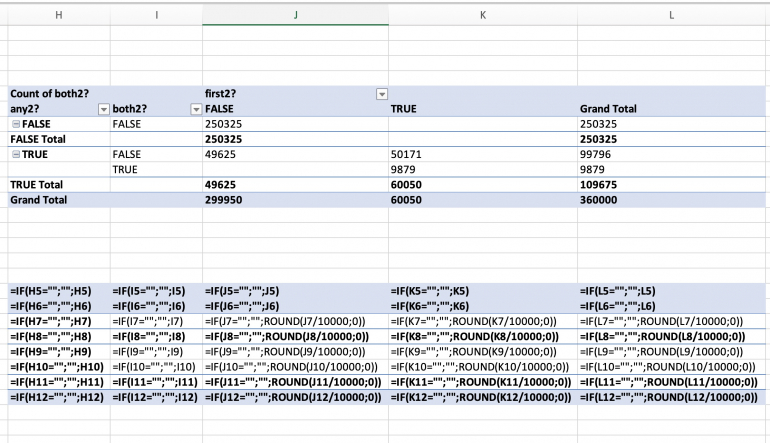
INTERPRETATION
-
* In 11 (out of 36) possibilities any of the two dice has a 2.
* In 1 out of these 11 possibilites both dice are 2.
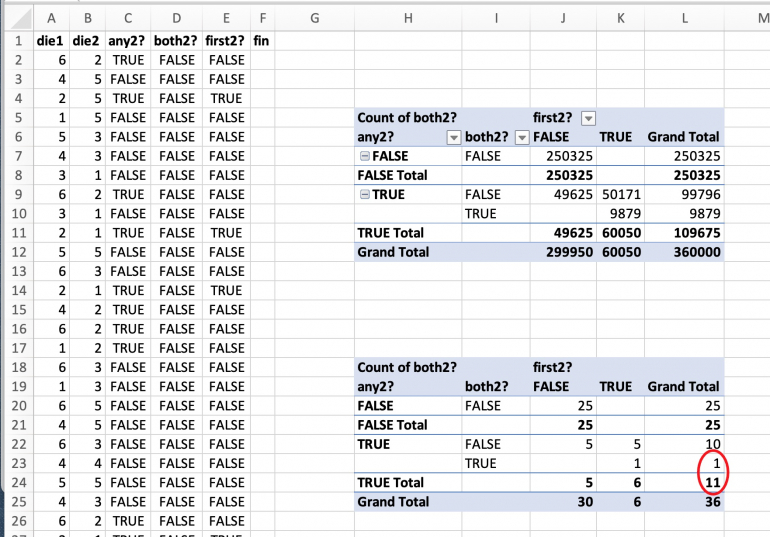
-
* In 6 (out of 36) possibilities any die has a two AND the first die is 2.
* In 1 out of these 6 possibilities both dice are 2.
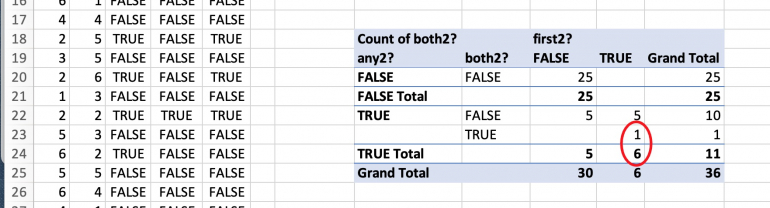
Is it possible to expand on this and account for times where a 2 might be rolled on one of the dice, but the number called out by the observer is the number on the other die?


