June 9th, 2022 at 7:41:48 AM
permalink
Quote: TravisRI like your fresh outlook and enthusiasm.
Is it possible to expand on this and account for times where a 2 might be rolled on one of the dice, but the number called out by the observer is the number on the other die?
link to original post
Thank you for your kind words.
I'm not completely sure whether I understand your request correctly:
-
* Two dice are rolled until at least one die is a 2.
* You check one of the dice. If it is a 2, you call out the other die.
* If the first check is not a 2, you call out that ("first") die.
Here all outcomes are sure things (100% probability).
If the first check revreals a 2, you call out the other die.
-
* If you announce "no 2", you know for sure (100%) that the first check has been 2, because at least one 2 was rolled.
* If you announce "2", you know for sure (100%) that the first check has been 2, because you would never announce a 2 if there was a die having "no 2".
If the first check reveals "no 2", you call out that.
-
* You now know for sure (100%) that the "other" die is a 2, because at least one 2 was rolled.
I added the announcement of "the other die" in my simulation.

The results are:
-
* In 10 (out of 36) possibilities any die has a 2, but the called out has not.
* In 10 out of these 10 possibilities (100%) only one die is a 2, not both.
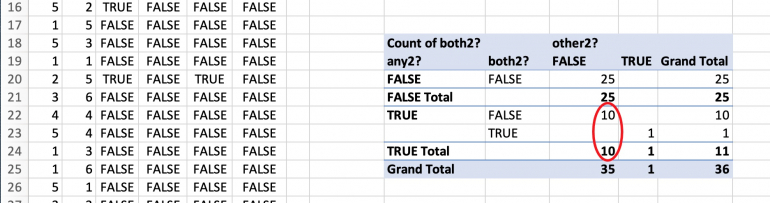
-
* In 1 (out of 36) possibilities both dice are 2, and a "2" has to be called out.
* This 1 possibility (100%) is the only possibility.
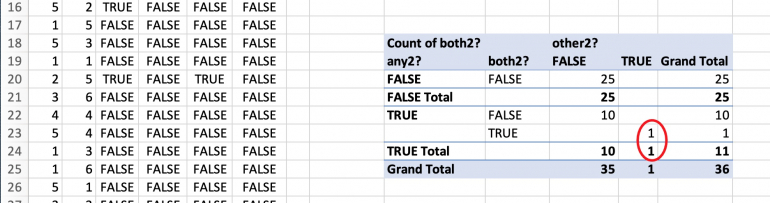
"When it comes to probability and statistics, intuition is a bad advisor. Don't speculate. Calculate." - a math textbook author (name not recalled)
June 9th, 2022 at 7:45:14 AM
permalink
Quote: TravisRI guess it's accounted for if you just go by the "first" die every time...... it's funny how choosing the "first" die every time is actually the model that simulates calling out a random die... but it also makes perfect sense
link to original post
I think you gave the right answer.
The "first" die is not a property permanently attached to any one of the two dice. It rather is the die that has to be called out first.
"When it comes to probability and statistics, intuition is a bad advisor. Don't speculate. Calculate." - a math textbook author (name not recalled)
December 3rd, 2024 at 7:32:26 PM
permalink
One of my favorite YouTube channels Mind Your Decisions has a video on this question. I hope Alan, wherever he may be, is able to watch it.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 4th, 2024 at 12:09:24 AM
permalink
You absolute B. Years of therapy undone with this one post!Quote: WizardOne of my favorite YouTube channels Mind Your Decisions has a video on this question. I hope Alan, wherever he may be, is able to watch it.
link to original post
I'll say it again. Without the calling rules being known, it is impossible to answer with any certainty.
And with that, I add a blocking line to my hosts file, change my password here to one I won't remember, and bid you farewell.
Psalm 25:16
Turn to me and be gracious to me, for I am lonely and afflicted.
Proverbs 18:2
A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.
December 4th, 2024 at 3:19:49 AM
permalink
it irritates me that the analysis use the "for one" payout instead of "to one"
I just feel that if you are trying to teach probability, you don't start off with the "for one" business, which if you do, you need to explain it. Which as a matter of fact, the video does not. Many students will go away now unable to correctly determine the proper payout for a given probability.
maybe it's just me, the analysis is correct
I just feel that if you are trying to teach probability, you don't start off with the "for one" business, which if you do, you need to explain it. Which as a matter of fact, the video does not. Many students will go away now unable to correctly determine the proper payout for a given probability.
maybe it's just me, the analysis is correct
the next time Dame Fortune toys with your heart, your soul and your wallet, raise your glass and praise her thus: “Thanks for nothing, you cold-hearted, evil, damnable, nefarious, low-life, malicious monster from Hell!” She is, after all, stone deaf. ... Arnold Snyder


