Best craps bonuses

Poll

3 votes (10.34%)
5 votes (17.24%)
2 votes (6.89%)
5 votes (17.24%)
3 votes (10.34%)
11 votes (37.93%)

29 members have voted

mustangsally
mustangsally
mustangsally
  • Threads: 25
  • Posts: 2463
Joined: Mar 29, 2011
March 30th, 2016 at 12:05:23 PM permalink
from
https://wizardofvegas.com/article/introductory-advantage-play2/

"To wit, the player flat-betting $10 on the Pass Line will extremely rarely, if ever, double $1,000 into $2,000."
<<<<>>>>
if ever??
well,
I think flat-betting would be boring but we could play faster as a team (more sleep)
or on a computer.
(yes, Sally's Casino offers this as a VIP only house bet)

makes one wonder how long it would take to double, on average, instead of just one bet at $1000 (much fun)

the poll is for fun only
what you feel the chances are to double a $1000 bankroll making just $10 flat bets playing craps
like candy
Sally
I Heart Vi Hart
TwoFeathersATL
TwoFeathersATL
TwoFeathersATL
  • Threads: 37
  • Posts: 3616
Joined: May 22, 2013
March 30th, 2016 at 12:17:01 PM permalink
I voted, I voted 'cause I saw a thread by Sally.
Don't see many of dem things.
I didn't do the math....
Youuuuuu MIGHT be a 'rascal' if.......(nevermind ;-)...2F
Joeman
Joeman
Joeman
  • Threads: 36
  • Posts: 2454
Joined: Feb 21, 2014
March 30th, 2016 at 12:41:15 PM permalink
I voted 1 in 108. No math just a WAG.

Quote: Article

To wit, the player flat-betting $10 on the Pass Line will extremely rarely, if ever, double $1,000 into $2,000.

However, on its face, I agree with this statement, but maybe not for the reasons the author intended. As Sally alluded to, this sounds like a tedious process. Also, I doubt that the player who brings $1000 to the table will just bet $10 on the PL until he doubles up or is broke.

Actually, the more I think about it, the less I like my guess. It's probably much more likely. But I'll leave the math to those who have more time/intellect/software than I.
"Dealer has 'rock'... Pay 'paper!'"
Romes
Romes
Romes
  • Threads: 29
  • Posts: 5624
Joined: Jul 22, 2014
March 30th, 2016 at 1:08:58 PM permalink
Variance for even money bet such as the pass line is 1. Thus, OriginalSD = 1*10 = 10. Avg House Edge = -1.41%. AvgBet = $10.

EV(x) = x*AvgBet*HouseEdge
SD(x) = Sqrt(x) * OriginalSD, where OriginalSD = 1*10 = 10

EV at 1 game = -$0.14, plus or minus Sqrt(1)*OriginalSD = 1*10 = $10.... 3SD is plus or minus $30.

EV at 100 games = -$14.10, plus or minus Sqrt(100) * 10 = 10 * 10 = $100... 3SD is plus or minus $300.

EV at 1,000 games = -$141.00, plus or minus Sqrt(1000) * 10 = $316.23... 3SD is plus or minus $948.69.

EV at 5,000 games = -$705.00, plus or minus Sqrt(5000) * 10 = $707.12... 2SD is plus or minus $1414.24... 3SD is plus or minus $2121.36

Here.

At this point we see it IS possible to be up $1,000... essentially doubling our starting bankroll of $1,000 to $2,000... Whilst we EXPECT to be down $705 after 5,000 throws, there is a chance we'll be on the right curve of variance and be up $1,000 at about 2.5 Standard Deviations to the right.

Thus, I'll conclude it is possible, but you have to be about 2.5 standard deviations up after about 5,000 games.
Playing it correctly means you've already won.
VladsGiants
VladsGiants
VladsGiants
  • Threads: 1
  • Posts: 25
Joined: May 20, 2015
March 30th, 2016 at 1:20:47 PM permalink
My guess is 1 in 8. Betting $10 one would need 100 more wins than losses to win $1000. If you take 1000 bets, for example, this would require 550 wins and 450 losses. 55% wins after 1000 bets at -1.4% EV doesn't sound that "extremely rare" to me. It seems reasonable that 7 out of 8 times one would have 100 more losses than wins before 100 more wins than losses.
DanMahoney
DanMahoney
DanMahoney
  • Threads: 7
  • Posts: 76
Joined: May 24, 2014
March 30th, 2016 at 1:24:03 PM permalink
Of course it all depends on who is tossing the dice. If my buddy LID or even dicesitter is tossing it would be more along the lines of 1 in 2 of doubling my BR (insert pic here for my new friend wizardofnothing).
mustangsally
mustangsally
mustangsally
  • Threads: 25
  • Posts: 2463
Joined: Mar 29, 2011
March 30th, 2016 at 1:58:02 PM permalink
Quote: Romes

Thus, I'll conclude it is possible, but you have to be about 2.5 standard deviations up after about 5,000 games.

interesting
about like this

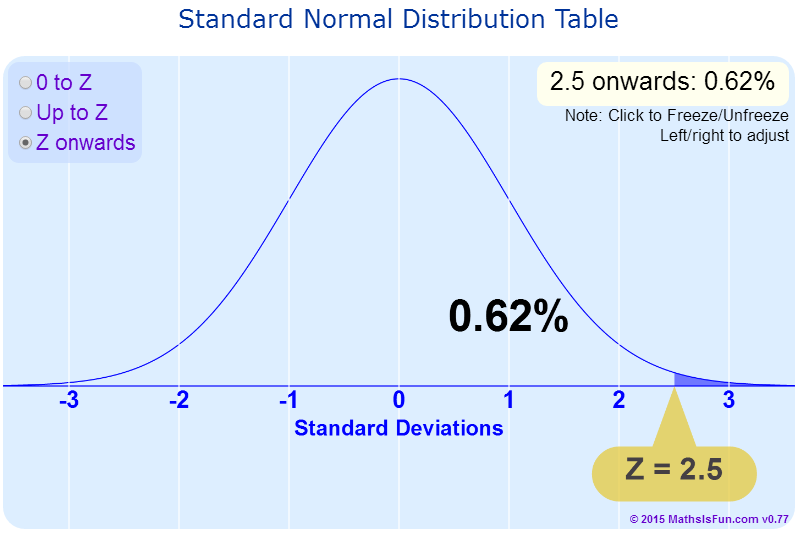
pic from
https://www.mathsisfun.com/data/standard-normal-distribution-table.html

I would think at 5,000 games one would have about
a 50/50 chance of either still playing or ruin-success
that is a calculation for Excel for later

Sally
I Heart Vi Hart
ThatDonGuy
ThatDonGuy
ThatDonGuy
  • Threads: 122
  • Posts: 6738
Joined: Jun 22, 2011
March 30th, 2016 at 2:28:00 PM permalink

Assume the problem asks for the probability of doubling $1000 before losing the whole $100 using just $10 Pass Line bets, this is a straightforward Gamblers Ruin problem with success limit = failure limit = 100 and event probability = 244/495, so the failure/success ratio is 251/244, and the answer is
((251/244)100 - 1) / ((251/244)200 - 1) = about 1 / 17.9195775.

That surprised me - I would have said that the number of bets needed, combined with the house edge, would have resulted in busting a lot more than 17 times out of every 18.

rushdl
rushdl
rushdl
  • Threads: 9
  • Posts: 177
Joined: Jan 15, 2016
March 30th, 2016 at 2:37:33 PM permalink
near zero chance, correct answer not available.
All you are doing is flat betting yourself down to $859 by betting on every shooter. Variance may get friendly with you at some point but nah this cant happen normally.

Also noted this:
'The Kelly Criterion exists to determine the Optimal bet sizing based on the percent advantage and variance".

Well, if you know how to "calculate" the variance you are to say the least pretty good at math. I cant believe I read that.
Ayecarumba
Ayecarumba
Ayecarumba
  • Threads: 236
  • Posts: 6763
Joined: Nov 17, 2009
March 30th, 2016 at 3:29:17 PM permalink
Quote: ThatDonGuy


Assume the problem asks for the probability of doubling $1000 before losing the whole $100 using just $10 Pass Line bets, this is a straightforward Gamblers Ruin problem with success limit = failure limit = 100 and event probability = 244/495, so the failure/success ratio is 251/244, and the answer is
((251/244)100 - 1) / ((251/244)200 - 1) = about 1 / 17.9195775.

That surprised me - I would have said that the number of bets needed, combined with the house edge, would have resulted in busting a lot more than 17 times out of every 18.



It's not that surprising when you look at it this way:
If your bankroll is $18k, and you split it into 18, $1k double or bust sessions if $10 flat betting, you might win $1k and lose $17k for a net loss of $16k. That seems about right for my craps table experience.
Simplicity is the ultimate sophistication - Leonardo da Vinci
mustangsally
mustangsally
mustangsally
  • Threads: 25
  • Posts: 2463
Joined: Mar 29, 2011
March 30th, 2016 at 3:38:13 PM permalink
Quote: ThatDonGuy


((251/244)100 - 1) / ((251/244)200 - 1) = <snip>

That surprised me

for doubling a bankroll with simple flat-bet even money win/lose bets
this works well too I have used for some time

(q/p)^unit+1 for 1 in X
and
1/(q/p)^unit+1 = probability

calling wolfram alpha for an exact answer

some like to B exact

http://www.wolframalpha.com/input/?dataset=&equal=Submit&i=(251%2F244)%5E100%2B1
I Heart Vi Hart
DeMango
DeMango
DeMango
  • Threads: 36
  • Posts: 2958
Joined: Feb 2, 2010
March 31st, 2016 at 12:40:23 AM permalink
delete
When a rock is thrown into a pack of dogs, the one that yells the loudest is the one who got hit.
DeMango
DeMango
DeMango
  • Threads: 36
  • Posts: 2958
Joined: Feb 2, 2010
March 31st, 2016 at 12:41:36 AM permalink
Quote: DanMahoney

Of course it all depends on who is tossing the dice. If my buddy LID or even dicesitter is tossing it would be more along the lines of 1 in 2 of doubling my BR (insert pic here for my new friend wizardofnothing).



Thanks for another humorous post, even if few, very few, of us get it. Don't be a stranger, I love insults no one else gets!
When a rock is thrown into a pack of dogs, the one that yells the loudest is the one who got hit.
Steen
Steen
Steen
  • Threads: 0
  • Posts: 126
Joined: Apr 7, 2014
March 31st, 2016 at 1:31:19 AM permalink
I vote 1 in 18 but I cheated with this:



If Beginning new session Then
   bankroll = 1000 :
   autotake full odds = false
EndIf

If comeout roll Then bet 10 on passline EndIf

If bankroll < 10 Or bankroll >= 2000 Then
   start new session
EndIf


View the results in the Sessions Log - Ending Bankroll.


In a run of 9076 sessions, 493 doubled the bankroll to $2000. That's 1 in 18.41

There were over 190 million rolls, averaging 20,988 rolls per session. Assuming an average roll rate of 120 rolls/hr that's an average of 174.9 hours per session -- basically a whole week per session.

Assuming the goal was to double or bust, the bankroll histogram is not a bell curve but just two outcomes with the $2000 outcome lying 4.17 standard deviations above the average bankroll of 108.64

In a second run, I added some code to measure the time between winning sessions. I didn't let it run as long but as an example the longest dry spell was 65 losing sessions. At an average one week per session that's over one year and three months of back-to-back losing sessions! That's $65,000 of losses waiting for the next $1000 win.

Steen
Last edited by: Steen on Mar 31, 2016
mustangsally
mustangsally
mustangsally
  • Threads: 25
  • Posts: 2463
Joined: Mar 29, 2011
March 31st, 2016 at 8:07:56 AM permalink
very nice
boring play cuz too much time to wait

try the Marty next
https://wizardofvegas.com/forum/gambling/craps/25412-double-1-000-into-2-000-part-2/#post522041

have fun!

added a pass line success ruin table
units = bankroll/bet
example:
1000/10=100units
for pass line
Bank UnitDouble10 inRuin
10.49292929320.290.507070707
20.48586141320.580.514138587
30.47879918420.890.521200816
40.47174541921.200.528254581
50.46470291821.520.535297082
60.45767446521.850.542325535
70.45066281922.190.549337181
80.44367071322.540.556329287
90.43670085122.900.563299149
100.42975590123.270.570244099
110.42283849123.650.577161509
120.41595120724.040.584048793
130.4090965924.440.59090341
140.40227712924.860.597722871
150.3954952625.280.60450474
160.38875336425.720.611246636
170.38205375926.170.617946241
180.37539870426.640.624601296
190.36879038927.120.631209611
200.3622309427.610.63776906
210.35572241128.110.644277589
220.34926678228.630.650733218
230.34286596329.170.657134037
240.33652178529.720.663478215
250.33023600330.280.669763997
260.32401029430.860.675989706
270.31784625531.460.682153745
280.31174540232.080.688254598
290.30570917232.710.694290828
300.29973891833.360.700261082
310.29383591434.030.706164086
320.28800135134.720.711998649
330.28223633835.430.717763662
340.27654190336.160.723458097
350.27091899436.910.729081006
360.26536847837.680.734631522
370.25989114438.480.740108856
380.254487739.290.7455123
390.2491587840.140.75084122
400.24390493941.000.756095061
410.23872665941.890.761273341
420.23362434842.800.766375652
430.22859834243.740.771401658
440.22364890844.710.776351092
450.21877624345.710.781223757
460.21398047946.730.786019521
470.20926168247.790.790738318
480.20461985748.870.795380143
490.20005494749.990.799945053
500.19556683651.130.804433164
510.19115535352.310.808844647
520.18682027153.530.813179729
530.18256131154.780.817438689
540.17837814656.060.821621854
550.17427039757.380.825729603
560.17023764458.740.829762356
570.16627941960.140.833720581
580.16239521661.580.837604784
590.15858448763.060.841415513
600.15484664864.580.845153352
610.15118108166.150.848818919
620.14758713367.760.852412867
630.14406412269.410.855935878
640.14061133571.120.859388665
650.13722803472.870.862771966
660.13391345474.680.866086546
670.13066680976.530.869333191
680.12748729178.440.872512709
690.12437407180.400.875625929
700.12132630382.420.878673697
710.11834312784.500.881656873
720.11542366686.640.884576334
730.11256703288.840.887432968
740.10977232291.100.890227678
750.10703862993.420.892961371
760.10436503295.820.895634968
770.10175060798.280.898249393
780.099194421100.810.900805579
790.096695539103.420.903304461
800.094253022106.100.905746978
810.091865927108.850.908134073
820.089533314111.690.910466686
830.087254238114.610.912745762
840.085027758117.610.914972242
850.082852934120.700.917147066
860.08072883123.870.91927117
870.078654511127.140.921345489
880.076629049130.500.923370951
890.074651519133.960.925348481
900.072721003137.510.927278997
910.070836589141.170.929163411
920.068997373144.930.931002627
930.067202456148.800.932797544
940.06545095152.790.93454905
950.063741975156.880.936258025
960.062074658161.100.937925342
970.060448138165.430.939551862
980.058861563169.890.941138437
990.057314089174.480.942685911
1000.055804887179.200.944195113
1010.054333135184.050.945666865
Last edited by: mustangsally on Mar 31, 2016
I Heart Vi Hart
jeffy8
jeffy8
jeffy8
  • Threads: 0
  • Posts: 3
Joined: Dec 6, 2015
May 5th, 2016 at 8:00:19 PM permalink
Anyone care to simulate with D'Alembert? bet 10 L bet 20 L bet 30 L bet 40 L bet 50 W bet 40 W bet 30 W bet 20 W bet 10 how long to gain 200$ on 1000$ buy-in? maybe more importantly- how many times gain 200-250$ vs. busting with 1000? and how about DP vs. Pass? how about bet opposite of whichever just won ( P/DP )? so many questions, I know, I know... are the answers worth their weight in chips?
Wizardofnothing
Wizardofnothing
Wizardofnothing
  • Threads: 121
  • Posts: 3493
Joined: Jul 3, 2015
May 5th, 2016 at 8:06:11 PM permalink
Wow you joined 6 months ago and waited for this for your first post?
Anyway/ welcome!
No longer hiring, don’t ask because I won’t hire you either
Steen
Steen
Steen
  • Threads: 0
  • Posts: 126
Joined: Apr 7, 2014
May 5th, 2016 at 11:03:06 PM permalink
Quote: jeffy8

Anyone care to simulate with D'Alembert? bet 10 L bet 20 L bet 30 L bet 40 L bet 50 W bet 40 W bet 30 W bet 20 W bet 10 how long to gain 200$ on 1000$ buy-in? maybe more importantly- how many times gain 200-250$ vs. busting with 1000? and how about DP vs. Pass? how about bet opposite of whichever just won ( P/DP )? so many questions, I know, I know... are the answers worth their weight in chips?


I ran a few simulations using this:

' Simple D'Alembert on Passline

If Beginning new session Then
   bankroll = 1000 :
   autotake full odds = false
EndIf

If bankroll < 10 Or bankroll >= 1200 Then '<-- bust or win 200+
   start new session
EndIf

If passline loses Then
   bet last passline + 10 on passline
ElseIf passline wins Then
   bet last passline - 10 on passline
EndIf
If comeout roll And passline = 0 Then bet 10 on passline EndIf


Running one Passline simulation of 10,327 sessions, I got an average session length of 186.82 rolls (about 1.56 hours at 120 rolls/hr). There were 8,197 winning sessions (79.37%) which is a nice win rate but remember that the 21% chance to lose is for $1000.

Changing the code to Don't Pass w/o odds and running for 10,565 sessions, I got an average session length of 192.12 rolls (about 1.6 hours). The average session length is understandably longer because the Don't Pass resolves less often. There were 8,739 winning sessions (79.31%).

As for betting opposite of whichever side just won, how do you propose to handle the come-out 12? Assuming you want to bet passline if a 12 rolls, then in a simulation of 10,154 sessions, I got an average session length of 332.28 rolls (about 2.77 hours). There were 7,721 winning sessions (76.04%).

' D'Alembert on Passline/Don't Pass
' Bet opposite whichever won last

If Beginning new session Then
   bankroll = 1000 :
   autotake full odds = false :
   autolay full odds = false
EndIf

If bankroll < 10 Or bankroll >= 1200 Then '<-- bust or win 200+
   start new session
EndIf

If passline wins Or dontpass wins Then
   cs1 = cs1 + 10
ElseIf passline loses Or dontpass loses Then
   cs1 = cs1 - 10
EndIf

If shooter passes Then
   bet cs1 on dontpass :
   passline = 0
ElseIf shooter misses Then
   bet cs1 on passline :
   dontpass = 0
EndIf

If passline = 0 And dontpass = 0 Then
   If comeout roll Then bet 10 on passline : cs1 = 10 EndIf
EndIf


Hope that helps. Are the answers worth their weight in chips? You'll have to judge for yourself.

Steen
Last edited by: Steen on May 6, 2016
OnceDear
OnceDear
OnceDear
  • Threads: 64
  • Posts: 7543
Joined: Jun 1, 2014
May 5th, 2016 at 11:51:37 PM permalink
Quote: rushdl

near zero chance, correct answer not available.
All you are doing is flat betting yourself down to $859 by betting on every shooter. Variance may get friendly with you at some point but nah this cant happen normally.

Also noted this:
'The Kelly Criterion exists to determine the Optimal bet sizing based on the percent advantage and variance".

Well, if you know how to "calculate" the variance you are to say the least pretty good at math. I cant believe I read that.

PMSL that rushdl thinks he knows better than MustangSally at Craps and/or probability calculations.

Quote:

Well, if you know how to "calculate" the variance you are to say the least pretty good at math. I cant believe I read that.

If YOU knew what variance is, then YOU would know it's easy to "calculate".

Rush, Dude. Sally can eat most of the maths guys here for breakfast. Don't cross her.
Last edited by: OnceDear on May 6, 2016
Psalm 25:16 Turn to me and be gracious to me, for I am lonely and afflicted. Proverbs 18:2 A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.
OnceDear
OnceDear
OnceDear
  • Threads: 64
  • Posts: 7543
Joined: Jun 1, 2014
May 6th, 2016 at 12:30:04 AM permalink
Quote: jeffy8

Anyone care to simulate with D'Alembert? bet 10 L bet 20 L bet 30 L bet 40 L bet 50 W bet 40 W bet 30 W bet 20 W bet 10 how long to gain 200$ on 1000$ buy-in? maybe more importantly- how many times gain 200-250$ vs. busting with 1000? and how about DP vs. Pass? how about bet opposite of whichever just won ( P/DP )? so many questions, I know, I know... are the answers worth their weight in chips?


Can't be bothered to sim it, but from my rule of thumb...

For 200 gain
P<=1000/1200 = 83%

For 250 gain
P<=1000/1250 = 80%

Less a bit for HE

Quote:

How long

is a piece of string?
Psalm 25:16 Turn to me and be gracious to me, for I am lonely and afflicted. Proverbs 18:2 A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.
Steen
Steen
Steen
  • Threads: 0
  • Posts: 126
Joined: Apr 7, 2014
May 6th, 2016 at 12:15:07 PM permalink
Correction: The code I posted for betting on opposite that won last was actually for the Contra D'Alembert. Here's corrected code for the D'Alembert:

' D'Alembert on Passline/Don't Pass
' Bet opposite whichever won last

If Beginning new session Then
   bankroll = 1000 :
   autotake full odds = false :
   autolay full odds = false
EndIf

If bankroll < 10 Or bankroll >= 1200 Then '<-- bust or win 200+
   start new session
EndIf

If passline wins Or dontpass wins Then
   cs1 = cs1 - 10
ElseIf passline loses Or dontpass loses Then
   cs1 = cs1 + 10
EndIf
If cs1 < 10 Then cs1 = 10 EndIf

If shooter passes Then
   bet cs1 on dontpass :
   passline = 0
ElseIf shooter misses Then
   bet cs1 on passline :
   dontpass = 0
ElseIf comeout roll Then
   bet cs1 on passline : ' default bet
   dontpass = 0
EndIf


Ran one simulation yielding an average of 178.11 rolls per session (about 1.48 hrs) and 79.2% winning sessions.

It's interesting to note that the average session length for Contra D'Alembert is almost twice that of the D'Alembert and that Contra D'Alembert also yields fewer winning sessions. Even so, the average loss per dollar wagered (EV) is the same for both. The only way to improve on that would be to take/lay odds.

Steen
jeffy8
jeffy8
jeffy8
  • Threads: 0
  • Posts: 3
Joined: Dec 6, 2015
May 11th, 2016 at 9:49:43 PM permalink
thank you both for the responses-- I assume a lower starting bankroll and lower win goal will end up with numbers roughly equivalent to those ascertained by the wincraps code--- left wondering, with a starting bank of, say, 8000$, how many decisions [P/DP/opp previous] until bust? or can we expect a net win at some point with enough of a bank?
jeffy8
jeffy8
jeffy8
  • Threads: 0
  • Posts: 3
Joined: Dec 6, 2015
May 11th, 2016 at 9:58:28 PM permalink
thanks for the welcome-- I've enjoyed reading the posts here for over a year, I guess, and appreciate those who can perform the math and explain things eloquently---anyway I didn't have much to add-- so silence is best-- I've stopped playing mostly, but I still believe a simple D'Alembert, stretched deep enough, can beat craps or bacc.
beachbumbabs
beachbumbabs
beachbumbabs
  • Threads: 101
  • Posts: 14268
Joined: May 21, 2013
May 12th, 2016 at 2:32:11 AM permalink
Quote: jeffy8

thanks for the welcome-- I've enjoyed reading the posts here for over a year, I guess, and appreciate those who can perform the math and explain things eloquently---anyway I didn't have much to add-- so silence is best-- I've stopped playing mostly, but I still believe a simple D'Alembert, stretched deep enough, can beat craps or bacc.



Welcome to the forum, jeffy, and feel free to speak up more often.
If the House lost every hand, they wouldn't deal the game.
AxelWolf
AxelWolf
AxelWolf
  • Threads: 170
  • Posts: 22690
Joined: Oct 10, 2012
May 12th, 2016 at 2:45:40 AM permalink
Quote: OnceDear



Rush, Dude. Sally can eat most of the maths guys here for breakfast. .

I'm sure she has.
♪♪Now you swear and kick and beg us That you're not a gamblin' man Then you find you're back in Vegas With a handle in your hand♪♪ Your black cards can make you money So you hide them when you're able In the land of casinos and money You must put them on the table♪♪ You go back Jack do it again roulette wheels turinin' 'round and 'round♪♪ You go back Jack do it again♪♪
Asswhoopermcdaddy
Asswhoopermcdaddy
Asswhoopermcdaddy
  • Threads: 88
  • Posts: 570
Joined: Nov 30, 2009
May 14th, 2016 at 4:35:26 PM permalink
1 in 18? I'll bet the over in real life.
JoelDeze
JoelDeze
JoelDeze
  • Threads: 49
  • Posts: 467
Joined: Apr 20, 2016
May 16th, 2016 at 7:26:04 PM permalink
Example 40-roller Session

Roller# of RollsWonLostNet
115$20.00 $10.00 $10.00
219$30.00 $10.00 $20.00
36$0.00 $10.00 ($10.00)
48$40.00 $10.00 $30.00
511$0.00 $10.00 ($10.00)
68$0.00 $10.00 ($10.00)
72$0.00 $10.00 ($10.00)
87$0.00 $10.00 ($10.00)
93$0.00 $10.00 ($10.00)
109$0.00 $10.00 ($10.00)
1120$40.00 $10.00 $30.00
124$10.00 $10.00 $0.00
138$0.00 $10.00 ($10.00)
1418$20.00 $10.00 $10.00
155$10.00 $10.00 $0.00
165$0.00 $10.00 ($10.00)
176$10.00 $10.00 $0.00
189$0.00 $10.00 ($10.00)
196$30.00 $10.00 $20.00
203$0.00 $20.00 ($20.00)
212$0.00 $10.00 ($10.00)
226$0.00 $10.00 ($10.00)
233$0.00 $10.00 ($10.00)
2423$50.00 $20.00 $30.00
259$10.00 $10.00 $0.00
262$0.00 $10.00 ($10.00)
277$0.00 $10.00 ($10.00)
285$0.00 $10.00 ($10.00)
2922$70.00 $10.00 $60.00
3012$0.00 $10.00 ($10.00)
316$20.00 $10.00 $10.00
3231$50.00 $20.00 $30.00
336$10.00 $10.00 $0.00
345$0.00 $20.00 ($20.00)
3515$10.00 $10.00 $0.00
3635$70.00 $20.00 $50.00
374$0.00 $20.00 ($20.00)
388$20.00 $10.00 $10.00
3912$20.00 $10.00 $10.00
407$30.00 $10.00 $20.00
Total392$570.00 $460.00 $110.00


This session net $110 over 392 rolls. The first 20 rollers combined to net $0. The second 20 rollers showcased 4 hot rollers (1 in 5) and combined for +$110 on flat bets of $10 over the duration.

So, to answer this question, in this scenario it would have taken approx. 392 rolls to double my bank roll. How? I would have given $100 to 10 people at the table and bought them all a Johnny Walker Black for $10 each.
“It’s a dog eat dog world out there and I’m wearing milkbone underwear .” – Norm Peterson
mustangsally
mustangsally
mustangsally
  • Threads: 25
  • Posts: 2463
Joined: Mar 29, 2011
June 26th, 2018 at 11:44:07 AM permalink
Quote: mustangsally

boring play cuz too much time to wait

this can now be easily calculated online
https://sites.google.com/view/krapstuff/risk-of-ruin
turning $1000 into $2000 flat betting $10
in units: 100 to 200 betting 1

section: 1r
> gambler.ruin2(244/495,200,"craps pass line. No odds",0)
[1] "craps pass line. No odds"
[1] "(in units)stake:100, target:200, attempt gain:100"
[1] "p(goal):0.0558048871176, 1 in:17.9195775075, p(ruin):0.944195112882, avg.trials:6282.188"

section: 2r
> gambler.ruin(100,100, 244/495, "Craps pass line 0x odds")
[1] "Craps pass line 0x odds. Stake:100, Target:200"
[1] "p(goal):0.0558048871177, 1 in:17.9195775075, p(ruin):0.944195112882"
[1] "mean Trials:6282.19, mean given Goal:6282.19, mean given Ruin:6282.19"

each pass line decision takes about 3.375 rolls on average
that is why this experiment would take a long time

I think the statement in the OP should have been written about 00 Roulette
that returns this
p(goal):2.65606933984e-05, 1 in:37,649.6
yes, hardly ever
"To wit, the player flat-betting $10 on the Pass Line will extremely rarely, if ever, double $1,000 into $2,000."

> gambler.ruin(100,100,18/38, "00 Roulette evens bet")
[1] "00 Roulette evens bet. Stake:100, Target:200"
[1] "p(goal):2.65606933984e-05, 1 in:37649.619496, p(ruin):0.999973439307"
[1] "mean Trials:1899.9, mean given Goal:1899.9, mean given Ruin:1899.9"

time and space
Sally
I Heart Vi Hart
charliepatrick
charliepatrick
charliepatrick
  • Threads: 39
  • Posts: 3017
Joined: Jun 17, 2011
June 26th, 2018 at 2:31:44 PM permalink
Not very scientific but I ran two trials - the first was trying to double or bust 10 units 1 million times, then the second was using 100 units which corresponds with the original question.

Note the cost of each game is $1

Parms: No of trials:1000000 Starting Capital $10 Time:22:23:19:488
Overall Result: Hands: 99319932 Win: 429405 Lose: 570595
Parms: No of trials:1000000 Starting Capital $10 Time:22:23:43:21

Parms: No of trials:10000 Starting Capital $100 Time:22:25:46:943
Overall Result: Hands: 62919488 Win: 520 Lose: 9480
Parms: No of trials:10000 Starting Capital $100 Time:22:26:1:788

Thus I got about 1 in 18 which coincides with one of the answers given on the initial poll!

"Hands" means number of comeout rolls.
ChumpChange
ChumpChange
ChumpChange
  • Threads: 131
  • Posts: 5112
Joined: Jun 15, 2018
July 12th, 2018 at 8:27:54 PM permalink
Quote: jeffy8
Anyone care to simulate with D'Alembert? bet 10 L bet 20 L bet 30 L bet 40 L bet 50 W bet 40 W bet 30 W bet 20 W bet 10 how long to gain 200$ on 1000$ buy-in? maybe more importantly- how many times gain 200-250$ vs. busting with 1000? and how about DP vs. Pass? how about bet opposite of whichever just won ( P/DP )? so many questions, I know, I know... are the answers worth their weight in chips?


Quote: Steen

I ran a few simulations using this:


Running one Passline simulation of 10,327 sessions, I got an average session length of 186.82 rolls (about 1.56 hours at 120 rolls/hr). There were 8,197 winning sessions (79.37%) which is a nice win rate but remember that the 21% chance to lose is for $1000.

Changing the code to Don't Pass w/o odds and running for 10,565 sessions, I got an average session length of 192.12 rolls (about 1.6 hours). The average session length is understandably longer because the Don't Pass resolves less often. There were 8,739 winning sessions (79.31%).

As for betting opposite of whichever side just won, how do you propose to handle the come-out 12? Assuming you want to bet passline if a 12 rolls, then in a simulation of 10,154 sessions, I got an average session length of 332.28 rolls (about 2.77 hours). There were 7,721 winning sessions (76.04%).


Hope that helps. Are the answers worth their weight in chips? You'll have to judge for yourself.

Steen



Passline: 10,327 - 8,197 = 2,130 losses
-$2,130,000 (lose $1000) + $1,639,400 (win $200) = -$490,600

Don't Pass: 10,565 - 8,739 = 1,826 losses
-$1,826,000 (lose $1000) + $1,747,800 (win $200) = -$78,200

Opposite Bets: 10,154 - 7,721 = 2,433 losses
-$2,433,000 (lose $1000) + $1,544,200 (win $200) = -$888,800

I'll have to try that on the Don't Pass if at all.
RSS Feed
  • Jump to: