Poll
 | 4 votes (40%) | ||
 | 1 vote (10%) | ||
 | 5 votes (50%) | ||
| No votes (0%) | |||
| No votes (0%) | |||
| No votes (0%) | |||
| No votes (0%) |
10 members have voted
March 31st, 2016 at 8:06:49 AM
permalink
this is part 2 from
https://wizardofvegas.com/forum/gambling/craps/25403-double-1-000-into-2-000/
the poll is for fun like the other was
some will be surprised of course (like me!)
<<<>>>
poll question
is
what is the chance to
turn $1000 into $2000 betting the pass line using the Marty betting system.
<<<>>>
the original turn $1000 into $2000 flat betting the pass line
turned out to be very boring
now to add more excitement
the Marty!
we all love Marty
hehe
1st bet = $10 on the pass line
when lose bet $20 or double the last losing bet
no odds... huh
comps will be better than flat betting
when win a bet, go back to basic $10 bet
if can not bet double the last losing bet
bet it ALL!
Yahoo Yahoo!!
maybe it takes less time too (1+1)
and more can win more money
with Marty!
Mo Mo Mo
Go Go Go
Sally
https://wizardofvegas.com/forum/gambling/craps/25403-double-1-000-into-2-000/
the poll is for fun like the other was
some will be surprised of course (like me!)
<<<>>>
poll question
is
what is the chance to
turn $1000 into $2000 betting the pass line using the Marty betting system.
<<<>>>
the original turn $1000 into $2000 flat betting the pass line
turned out to be very boring
now to add more excitement
the Marty!
we all love Marty
hehe
1st bet = $10 on the pass line
when lose bet $20 or double the last losing bet
no odds... huh
comps will be better than flat betting
when win a bet, go back to basic $10 bet
if can not bet double the last losing bet
bet it ALL!
Yahoo Yahoo!!
maybe it takes less time too (1+1)
and more can win more money
with Marty!
Mo Mo Mo
Go Go Go
Sally
I Heart Vi Hart
March 31st, 2016 at 9:18:46 AM
permalink
What if you jump from $10 loss to $100 bet? Then from $100 bet to $300 bet, assuming loss again. Then from $300 bet to $800 bet? You lost 100+300+800, jhit happens. Start over, try that a gazillion times or so. I would do it but I don't know how ;-( cheers, just 2F...
Youuuuuu MIGHT be a 'rascal' if.......(nevermind ;-)...2F
March 31st, 2016 at 10:27:07 AM
permalink
If my equation solver is working properly, I get 45.620221%, or about 1 in 2.192.
March 31st, 2016 at 11:28:18 AM
permalink
the info I do have (due have) on the Marty for this poll is small but I like the average number of rolls to complete the experiment-challenge. looks to be abouts 546 rolls
from wincraps classic (goes good with skittles)
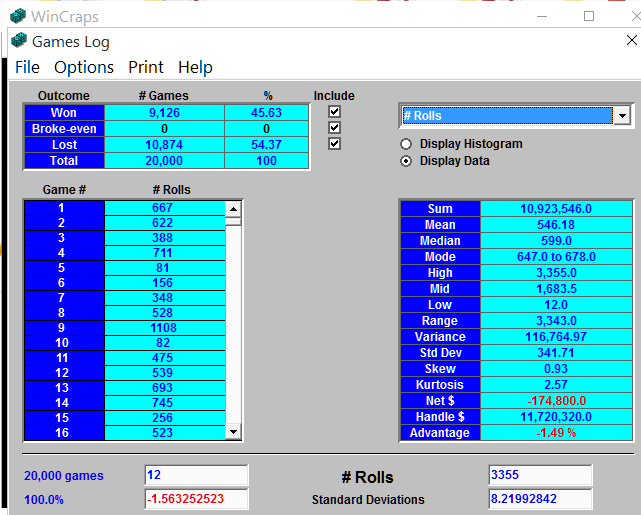
from wincraps classic (goes good with skittles)

I Heart Vi Hart
March 31st, 2016 at 1:54:12 PM
permalink
If Beginning new session Then
bankroll = 1000 :
autotake full odds = false
EndIf
If passline loses Then
Bet last passline * 2 on passline
ElseIf comeout roll Then
Bet $10 on passline
EndIf
If bankroll < 10 Or bankroll >= 2000 Then
start new session
EndIf
Last edited by: Steen on Mar 31, 2016
May 5th, 2016 at 11:46:08 PM
permalink
Quote: mustangsallythis is part 2 from
what is the chance to
turn $1000 into $2000 betting the pass line using the Marty betting system.
Oncedear rule of thumb applies very well indeed to low house edge, even money bets using Marty with a small base unit.
P=Initial Bankroll/(Target Profit+Initial Bankroll) . Approx.
P=1000/(1000+1000)
P=50%
1 in 2 (and a bit for house edge)
FAR FAR BETTER than 1 in 18 !!!!!!
Psalm 25:16
Turn to me and be gracious to me, for I am lonely and afflicted.
Proverbs 18:2
A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.
June 27th, 2018 at 10:55:00 AM
permalink
I was going to add my calculation from Excel (I think I lost it in a different folder, in other words I lost it!)Quote: ThatDonGuyIf my equation solver is working properly, I get 45.620221%, or about 1 in 2.192.
so as I have yet to convert Excel to online R use
*****
my sim data (in Excel) shows
Went Bust: 54.16200%
Hit Target: 45.83800% <<< 1 in 2.18
avg bet = $36.17
take that average bet and make it $40
flat betting $40 now shows this (remember 0 odds) (turning 25 units into 50)
> gambler.ruin(25,25, 244/495, "Craps pass line 0x odds")
[1] "Craps pass line 0x odds. Stake:25, Target:50"
[1] "p(goal):0.330236, p(ruin):0.669764"
[1] "mean Trials:600.237, mean given Goal:600.237, mean given Ruin:600.237"
https://sites.google.com/view/krapstuff/risk-of-ruin
section 2r.
p(goal):0.330236 is about 1 in 3 on average
much better (but expected)
*****
how does this compare to 100 units into 200 units
with the free odds bet?
well, I used some R code (and a Markov chain solution)
(will post that code online as soon as it is cleaned up)
It was my 1st attempt long ago.
I do way better now
I do way better now
##### suggest bankroll_target no lower than 20
# Gambler's Ruin - mean time in transient states
# and probabilities to target goal and ruin
title <- 'pass 345x odds. over-shoot target possible'
bankroll_target <- 200 # Enter bankroll target (in units)
bankroll_start <- (bankroll_target/2)
# Enter a different starting bankroll, default is 50% of target
##### do not change any below here
bankGainUnit <- (bankroll_target - bankroll_start)
startBr <- (bankroll_start) # for avg # of trials sum (from Q returns Index #)
states <- (bankroll_target + 7) # (target = 1st term))
#example target==20;(20+7)(over-shoot target states=7)
pass <- 244/495 # prob of win 1 unit flat bet (not enough for odds bet)
miss <- 251/495 # prob of loss 1 unit flat bet (not enough for odds bet)
SevenOut <- 196/495
Point <- 134/495
ptFourLoss <- 1/9
ptFiveLoss <- 2/15
ptSixLoss <- 5/33
nat <- 2/9
craps <- 1/9
target <- bankroll_target # absorbing state target goal EXACT
state2state <- (target - 1) #last state index
absorb_states <- target # begin absorb states
row.col_Names <- c(1:(states - 1),0)
# enter transition probability matrix
P <- matrix(rep(0,states^2), nrow=states, ncol=states,
dimnames = list(row.col_Names, row.col_Names))
# absorbing goal/ruin states = 1
for (i in target:states) {P[i, i] <- 1 }
# to ruin from 1:6 bank trying to double-up
for (i in 1:5) {P[i, states] <- miss }
P[6,states] <- ptSixLoss
# to pass - 1 to 5 bank double-up success
for (i in 1:5) {P[i, i * 2] <- pass }
# Point diag starts at P[6,13]
for (i in 6:state2state) {P[i,i + 7] <- Point }
# nat diag starts at P[6,7]
for (i in 6:state2state) {P[i,i + 1] <- nat }
# craps diag starts at P[6,5]
for (i in 6:state2state) {P[i,i - 1] <- craps }
# ptFourLoss diag starts at P[6,2]
for (i in 6:state2state) {P[i,i - 4] <- ptFourLoss }
# ptFiveLoss diag starts at P[6,1]
for (i in 6:state2state) {P[i,i - 5] <- ptFiveLoss }
# ptSixLoss diag starts at P[7,1]
for (i in 7:state2state) {P[i,i - 6] <- ptSixLoss }
#P # uncomment to show matrix
#print(formatC(P),quote=FALSE)
P_sums <- as.matrix(rowSums(P))
colnames(P_sums) <- list("total")
#print(P_sums)
# take sub-matrix for transient states to states
P.s <- P[1:state2state, 1:state2state]
#P.s
# take sub-matrix for transient states to absorbing states
P.t <- P[1:state2state, absorb_states:states]
#P.t
# compute mean number of revisits matrix S
Q <- solve(diag(state2state)-P.s)
#Q
# sum entries in Xth row of Q
sum(Q[startBr,])
#bankroll_start
#startBr #Index number
Q_sums <- as.matrix(rowSums(Q))
colnames(Q_sums) <- list("avg trials")
#print(Q_sums)
QT <- Q %*% P.t
#QT
goalG <- QT[1:state2state, 1:7]
#goalG
success_target <- as.matrix(rowSums(goalG))
colnames(success_target) <- list("p(target)")
#print(success_target)
ruinR <- QT[1:state2state, 8]
#ruinR
ruinR <- as.matrix(ruinR)
colnames(ruinR) <- list("p(ruin) ")
#print(ruinR)
S2Srow_names <- as.matrix(seq(1, (bankroll_target - 1), by=1 ))
colnames(S2Srow_names) <- list("bank")
#print(S2Srow_names)
final <- cbind(S2Srow_names, success_target, ruinR, Q_sums)
rownames(final) <- c()
#print(final)
data <- as.matrix(final[startBr, ])
colnames(data) <- list("data ")
print(title)
print(formatC(data,digits=10),quote=FALSE)
bankroll_target
bankGainUnit
Full 2x odds($10flat wit $25 odds on 6&8): p(target) 0.4229117 <<<lower than a Marty
345x odds: p(target) 0.4704061 <<< a bit higher than a Marty
*** note this is hitting target exactly *** most do and will not play this way
345x odds: p(target) 0.4647375755 where one can go over the target (from 20 to 26 units)
INTERESTING, I do say so
[1] "pass 345x odds. over-shoot target possible"
> print(sprintf("Bankroll target:%g, unit gain:%g",bankroll_target,bankGainUnit))
[1] "Bankroll target:200, unit gain:100"
> print(formatC(data,digits=10),quote=FALSE)
data
bank 100
p(target) 0.4647375755
p(ruin) 0.5352624245
avg trials 422.46213
[1] "pass 345x odds. Exact target"
> print(data)
data
bank 100.0000000
p(target) 0.4704061
p(ruin) 0.5295939
avg trials 413.7700891
> bankroll_target
[1] 200
> bankGainUnit
[1] 100
[1] "pass Full 2x odds. Exact target"
> print(data)
data
bank 100.0000000
p(target) 0.4229117
p(ruin) 0.5770883
avg trials 1077.0895754
> bankroll_target
[1] 200
> bankGainUnit
[1] 100
[1] "don't pass 345x odds. Exact target"
> print(data)
data
bank 100.0000000
p(target) 0.4713885
p(ruin) 0.5286115
avg trials 415.9557935
> bankroll_target
[1] 200
> bankGainUnit
[1] 100
this shows why Marty has been around for a long time
and keeps on being discovered
even to this day!
I am guessing that in truth
the Marty does have a place in the sun!
Sally
Last edited by: mustangsally on Jun 27, 2018
I Heart Vi Hart
June 27th, 2018 at 11:01:22 AM
permalink
I'll never forget the day I invented it. Made a paper profit of almost $1,000 playing Sic Bo. The next day, starting at $1 units, I was up $225 by lunch.
I simply couldn't believe no one had ever done this before. Of course, I gave it all back after lunch.
I simply couldn't believe no one had ever done this before. Of course, I gave it all back after lunch.
The older I get, the better I recall things that never happened


