Variance and Standard Deviation

Threads: 10
Posts: 905

Joined: Mar 12, 2011

May 22nd, 2013 at 6:11:36 PM permalink

Quote: s2dbaker

That is the meaning of standard deviation of a gaussian variate. There are several different variates, depending of the specific bet. All of them have properties called "standard deviation", and is a measure of the width of the probability distribution. But not with those numbers above....

7craps

7craps

Threads: 18
Posts: 1977

Joined: Jan 23, 2010

May 22nd, 2013 at 7:10:54 PM permalink

Quote: crapswoman
I am interested in learning more about the math formulas and how these formulas can be used in some craps situations.
For example, the situation of a line bet with different level of odds--since I assume the more odds multiple I take, the greater the variance.

But exactly how much variance and what does standard deviation mean in this analysis? This obviously relates to bankroll size, right?

Can you take me through some simple craps bets and use the math formulas for the concepts of variance and standard deviation?

Thanks.

Yep. More odds more variance.
Think of standard deviation as your bankroll movements compared to the average or EV.
some links
https://wizardofvegas.com/forum/gambling/tables/1213-variance-in-craps/

https://wizardofvegas.com/forum/gambling/betting-systems/2794-craps-strategy-investment-opportunity/11/#post46860

https://wizardofvegas.com/forum/gambling/tables/1376-starting-bankroll-and-strategy-craps/3/#post132971

Example: 60 $5 pass line bets with 0 odds
EV = (-7/495)*$5*60
you should get about -$4.24
One can not lose exactly that in 60 trials but that represents the theoretical average over many trials
and is about the center of all possible outcomes

your unitSD is very close to 1. We use 1.
1*$5*(square root of 60) = $ standard deviation over 60 wagers = $38.73
Now the photo of the normal curve shows the percentages with 1 SD away from the mean (EV) and 2 SDs and 3SDs etc.

So 1SD from the EV would be the EV + and - 1 SD (-4.24 +/- $38.73)
about 2/3 of 60 bet sessions would fall some where in that interval... a 1 SD range.
(This assumes that you have the bankroll or casino credit needed to make all 60 wagers)
The chances of being up 1SD or down 1SD are equal and there is nothing you can do about that with independent trials.

3SD	$111.94
2SD	$73.21
1SD	$34.48
EV	-$4.24
-1SD	-$42.97
-2SD	-$81.69
-3SD	-$120.42

The more odds taken the greater the number of trials are needed so this all works.
Otherwise the Skew of all the possible outcomes messes up what is 1 SD using the normal curve.
2X odds is safe (I know from seeing the distribution and the numbers)

Example: 60 $5 pass line bets with 2X odds ($10)
EV = (-7/495)*$5*60
you should get about -$4.24 (same as without odds)

your unitSD is very close to 2.86.
We use 2.86
2.86*$5*(square root of 60) = $ standard deviation over 60 wagers = $110.69
(I did not round up)

Now 1SD from the EV would be the EV + and - 1 SD (-4.24 +/- $110.69)
about 2/3 (68%) of 60 bet sessions would fall some where in that interval... a 1 SD range.
And a lot wider range than taking 0 odds

Good Luck with your studies
here is a handy table for odds and unitSD for pass line bets (Dpass are very close. I post when I find it.
I think guido111 also posted it somewhere)

Odds	unitSD	   avg bet
0	0.999900	1.00
1	1.893050	1.67
2	2.857880	2.33
Full 2	2.954695	2.47
3	3.840744	3.00
345X	4.915632	3.78
4	4.830647	3.67
5	5.824001	4.33
6	6.819298	5.00
7	7.815796	5.67
8	8.813087	6.33
9	9.810930	7.00
10	10.809171	7.67
20	20.800879	14.33
40	40.796487	27.67
50	50.795588	34.33
60	60.794984	41.00
80	80.794225	54.33
100	100.793768	67.67

using the EV and Standard Deviation to calculate Bankroll and Risk of Ruin requirements is the next step.
There are many threads here at WoV that covers that quite well
instead of 10x you spread or 3 times the number of bets you plan on making

In the above odds example I would add the EV(absolute value, remove the -)
to 2* the SD value for a Bankroll to survive 60 bets while having a Risk of Ruin (bust out)
at about 1 in 20 to 1 in 25
(1 in 20 means on average about 0 bust outs in 20 sessions 36% of the time and 2 or more bust outs in 20 sessions
about 26% of the time.)

$225 Bankroll (45 betting units) $5 pass with 2X odds bets for 60 bets (good 2 hours of play)
sim results
No. Sessions simulated = 1000000
Bankroll was busted . . = 4.037% of the time ( 40374)
Bankroll decreased . . = 51.679% of the time
Bankroll increased . . = 47.968% of the time

winsome johnny (not Win some johnny)

crapswoman

Threads: 2
Posts: 20

Joined: May 9, 2013

May 23rd, 2013 at 7:59:43 AM permalink

Thanks for your informative response, 7craps. Also for the links. I should have known there were previous threads that pertain to my questions and I should have done a search. There is a lot of stuff there.

crapswoman

Threads: 2
Posts: 20

Joined: May 9, 2013

May 24th, 2013 at 10:00:36 AM permalink

The quote below was taken from a different thread a few months ago:

Quote: 7craps
Can no one at this site other than goatcabin calculate anything other than HE and EV?
added: theC can and does too.
I know ME can also, but he seems not to get involved in these type of threads.

Well, I'm trying--thanks to your help and the help from other posters in reviewing earlier threads including those that you provided the links to.

I'm convinced that variance is MORE important than HE or EV--when playing a game with an expected loss. Variance is the best way to hopefully have a winning session. Though you are exposed to a greater loss, you do not have to be "as lucky" to have a winning session. (I read it stated this way a couple of times and it makes sense.)

So I am focusing more on calculating the variance and measuring that against the risk and, in turn, using that in determining bankroll size.

I am helped immensely by your response, 7craps, and from the posts of other people before you. THANKS! But also sometimes confused. Maybe I am making this harder than it needs to be.

I know I can use WinCraps (which I own and do use and which also has a great Help section) which can spit out some of the results. But I really want to understand the math behind the results. Maybe also develop some Excel sheets to input the information.

Now to my further questions. I hope I am not being obtuse. Since there are several questions below, as I am probably jumping around, I will underline the questions (which I just figured out how to do). Maybe this discussion may benefit others as well. Sorry for so many questions.

***

I understand your example above, 7craps, where you did one pass line bet. Very helpful! You showed clearly the following:

So 1SD from the EV would be the EV + and - 1 SD (-4.24 +/- $38.73)
about 2/3 of 60 bet sessions would fall some where in that interval... a 1 SD range.

I did not fully understand, however, how you arrived at the conclusion that about 2/3 of the 60 bet sessions would fall within the +/- 1 SD range. How is that determined? And what if I want to know how many of my bet sessions will fall within, say, 2 SD--

Is this where I would look at the bell curve that is included in the earlier response in this thread? Am I to use this bell curve in all cases for the percent of bet sessions that will fall within the appropriate SDs?

But what about the following comment--which would suggest I should not rely on this bell curve:

Quote: MangoJ
That is the meaning of standard deviation of a gaussian variate. There are several different variates, depending of the specific bet. All of them have properties called "standard deviation", and is a measure of the width of the probability distribution. But not with those numbers above...

***

To a second area of questioning--

I also follow the second example you gave with the $5 pass line bet and 2x odds. But then you included in this example your use of 2.86 for the SD--you called it the "unitSD." You also used in the first example the number "1"--since the unitSD from your "handy table" is nearly "1"

This "handy table" with "unitSD" going from 0 odds to 100x along with avg bets---How did you arrive at these numbers?

By the way, I've been looking for a similar table for the don't pass numbers which you said was posted previously. Have not found it yet. Still looking. Is this a table that I could replicate or produce myself in Excel?

***

Now to a third area--which I suppose is overlapping with the other areas of my questions--

I know the following:

For a wager that pays x:1 with a probability of winning p, the house edge and standard deviation (per unit bet and per 'root decision') are:

ev (house edge) = (x+1)*p - 1
standard deviation = (x+1)*Sqrt[p*(1-p)]

Would it be asking too much for you to show the use of these formulas in a different example--just to be sure that I have it correctly?

In thinking about using Excel and these formulas---

Is this where I could use the BINOMDIST function in Excel?

Which I have not gotten into yet, so I don't even know if and when I should use this Excel function.

And what does "binomial" mean versus "standard?"

I then saw this response from Alan Shank in another thread about these two formulas:

Quote: goatcabin
Those are correct, as far as they go. They give you the information, per unit bet, for ONE BET. However, as you make multiple bets, the Standard Deviation and the ev increase at different rates, the ev increasing at the same rate as the number of bets, but the SD increasing with the square root of the number of bets.

I regret that I got a little confused. Can you or Alan Shank or someone else help me with this comment?

I think this refers to a situation with successive, but overlapping bets, if I am not mistaken.

***

Maybe the thing to do is to look at a new example.

What if we take a somewhat common betting strategy or betting sequence as the following:

a. Bet $10 on the pass line
b. Point is established and take 5x odds
c. Bet $10 in the come
d. Different number is established for that come. Take 5x odds on that also.
e. Bet another $10 in the come
f. A third different number is established for that come. Take 5x odds on that as well.
g. Let's go ahead and do another come. Let's assume either a 4th new number is established or even one of the other previous numbers is hit. We again take 5x odds.

Is it possible to evaluate this betting sequence by using the math formulas to determine EV and variance/standard deviation over a number of wagers or is this where it is necessary and appropriate to use WinCraps?

***

One final question (for now)--though I think this has a simple answer and I may only be making this harder than it needs to be.

I have also seen the following:

standard deviation = Bet*(x+1)*Sqrt(p*(1-p)*n)

This formula is almost exactly the same, except "Bet" is included and also an "n" Is this formula supposed to indicate something a little different?

***

Sorry I got carried away. Maybe I should have broken this down in separate posts. Maybe I should sign up for a class!

You guys (and girls--such as mustangsally whose posts have been great also--and where has she been lately?)--you've been fabulous in helping me! Thanks!

MangoJ

Threads: 10
Posts: 905

Joined: Mar 12, 2011

May 24th, 2013 at 1:05:47 PM permalink

Quote: crapswoman
I have also seen the following:

standard deviation = Bet*(x+1)*Sqrt(p*(1-p)*n)

This formula is almost exactly the same, except "Bet" is included and also an "n" Is this formula supposed to indicate something a little different?

This is the standard deviation of a series of "n" bets with constant betsize "Bet", paying odds "x:1", and has a hit probability of "p".

Quote:

standard deviation = (x+1)*Sqrt[p*(1-p)]

This is obviously the same formula for n=1 and Bet=1. Meaning that this is the standard deviation "per bet" and "per square root decision".
(The funny term "per square root" comes from the fact that the standard deviation is proportional to sqrt(n) instead of n).

dicesitter

dicesitter

Threads: 32
Posts: 1157

Joined: Jan 17, 2013

May 24th, 2013 at 1:16:08 PM permalink

Crapswoman

IN terms of deciding what you want to bet and how much you want to bet. it is fairly simple how much do want to
lose.

Every one knows the odds and edges and there is no way in the normal course of things to escape that.

For every $100 you bet on the 6 & 8 you will lose $1.52
For every hundred dollars you bet on the 5 & 9 you will lose $4
For every $ 100 you bet in the field on a table that pays double on 2 & 12 you will lose $5.56

There is no bet or combination of bets that changes that.

If you want to control your loss , you bet the best bets you can.

In terms of how much money you need. Again how much can you either afford to lose , or how much
do you figure a casino trip is worth to you.

In my case i have a craps account, all my winnings go into it, and loses come out of it....to sustain it over
time i wont have a starting bet series more than 2% of my total, many think 1% is required.

If my account would be $5000 i could have a starting place of $100. that is pass line with odds and
a $30 6 & 8.

If i had $3000, i could only have a starting bet or series of bets of $60 and so on.

Remember this is a game of math..,.. what it is is what it is.

Dicesetter

crapswoman

Threads: 2
Posts: 20

Joined: May 9, 2013

May 24th, 2013 at 1:36:06 PM permalink

Thanks MangoJ for clearing up my confusion on the two formulas being the same--with the one formula for a "per bet" decision. I should have figured that out. Duh.

odiousgambit

odiousgambit

Threads: 327
Posts: 9729

Joined: Nov 9, 2009

May 24th, 2013 at 2:11:10 PM permalink

Quote: crapswoman
I know these can be complicated subjects...But exactly how much variance and what does standard deviation mean in this analysis?

Crapswoman, it strikes me that you are not math-phobic in the least and may have taken some college courses. Somehow statistical math was skipped, eh? Nonetheless, you are not experiencing the kind of non-comprehension someone who has taken little math usually displays. It seems you will master the material right away, impressive.

I have to ask where you are going with this, though? I guess it seems to me you must know you can enjoy craps and avoid playing it stupidly without delving in quite so deep. Having said that, you are surely making the Wizard and others quite happy with this interest.

Care to elaborate?

the next time Dame Fortune toys with your heart, your soul and your wallet, raise your glass and praise her thus: �Thanks for nothing, you cold-hearted, evil, damnable, nefarious, low-life, malicious monster from Hell!� She is, after all, stone deaf. ... Arnold Snyder

crapswoman

Threads: 2
Posts: 20

Joined: May 9, 2013

May 24th, 2013 at 2:35:44 PM permalink

Quote: dicesitter
IN terms of deciding what you want to bet and how much you want to bet. it is fairly simple how much do want to
lose.

Every one knows the odds and edges and there is no way in the normal course of things to escape that.
...
There is no bet or combination of bets that changes that.

If you want to control your loss , you bet the best bets you can.

I agree--to a great extent--what you say. But this statement does not go far enough.

Until recently, my exclusive focus was on the house edge just as you described, dicesitter. I knew what my ev was for the bets that I made. And I used this information as my yardstick in comparing bets and in selecting bets that were most advantageous (or least painful). I also knew intuitively that by taking odds, I was exposed to more risk--but also more potential gain.

But that focus ignored a very important consideration of craps play: variance.

Most bets do not lose the expected value on every roll or decision. So it is not a totally accurate statement to say (as you did) for every $100 bet on the 6 and 8, you will lose $1.52. It is an average of all possible outcomes. Individual outcomes may vary. They DO vary. And it is this variation that allows a player to do better--or worse--than the expected value.

If it was not for variance, then maybe no one would play craps. Since it is variance that allows us to win from time to time. Is "variance" the mathematical word for "luck?"

I am trying to understand more the math for the ***complete*** picture. We should not stop at only computing the expected value (ev). We should continue further and measure how the individual outcome deviates or varies from the ev. We then square those deviations to take an average to arrive at variance. Then we need to take the square root of the variance to arrive at standard variation. (Did I say that right??)

Since variance and standard variation are measurements of volatility, it is also a useful measurement of risk. Not instead of ev. But with ev.

I understand that if the outcomes deviate more from ev then the higher the standard deviation will be. I should say, more spread out. And if the standard deviation is lower, the outcomes will be less spread out (deviate less from ev).

Bets with a lower standard deviation are more stable and should be considered less risky when compared to bets with higher SD. HOWEVER, more stability means fewer chances to win--which could, as a consequence, be interpreted as a more risky strategy.

Since craps is a game of negative expectation (just as you said, dicesitter), then we need variance to win. But with a greater chance to win comes a greater chance to lose.

***

I have also been realistic about the size of my bankroll in comparison with my bets. I think too many people over-bet in relation to their bankroll. I wanted to quantify it a little more precisely based on the math.

I would like to know--assuming a specific bet sequence that I want to employ--what is the exposure to loss (and also potential for win) based on the standard deviation. Then assuming further--based on what is a reasonable or acceptable standard deviation for me--the percent of those bet sequences or trials which fall within that range and then make sure that I have the bankroll to cover it. There is still a percent that falls outside that range so that it may be my bankroll is not enough, and so maybe I will need to up my bankroll. I don't want to play too conservatively either.

crapswoman

Threads: 2
Posts: 20

Joined: May 9, 2013

May 24th, 2013 at 3:04:49 PM permalink

Quote: odiousgambit
Crapswoman, it strikes me that you are not math-phobic in the least and may have taken some college courses. Somehow statistical math was skipped, eh? Nonetheless, you are not experiencing the kind of non-comprehension someone who has taken little math usually displays. It seems you will master the material right away, impressive.

I have to ask where you are going with this, though? I guess it seems to me you must know you can enjoy craps and avoid playing it stupidly without delving in quite so deep. Having said that, you are surely making the Wizard and others quite happy with this interest.

Care to elaborate?

Thank you for the compliment. I should say encouragement.

I have taken a good deal of math in school. But just as you said, not statistical math. And it's been a long, long time. Kids. Non-math career. High-maintenance husband.

Speaking of my husband--he also plays craps, I think very intelligently. I mentioned in another post why we don't play at the same table at the same time. But we have talked about craps. My husband as guided me in some of my thinking. It was my interest in wanting know more about the math that caused me to get on this site.

I know I can enjoy craps and avoid playing stupidly without knowing near as much detail about the math. But it is also enjoyable to KNOW MORE what I can EXPECT with my play and to better EVALUATE what HAPPENED to me after my play session has ended.

As I said, this knowledge should better help me with determining proper bet size in relation to bankroll size.

It should also help me better determine a win goal and a loss limit. My husband has convinced me, however, this sort of money management does not insure against losses.

I mentioned before in my thread on "Books on Craps" that it is difficult to tell who are the experts and who are not on this site. I have some doubts about several of the members on this forum (and a few in particular) who call themselves experts. But when people respond to my questions about the math in an intelligent way, I begin to figure out who I should listen to and who I should not.

Thanks for your patience and your help.

crapswoman

Threads: 2
Posts: 20

Joined: May 9, 2013

May 24th, 2013 at 3:20:28 PM permalink

Quote: crapswoman
I have some doubts about several of the members on this forum (and a few in particular) who call themselves experts. But when people respond to my questions about the math in an intelligent way, I begin to figure out who I should listen to and who I should not.

That sure did come across sounding harsh. I did NOT mean to sound that way!

It is probably because in another thread I was referred to as "woman" in a demeaning way by Ahigh (since I think he was perturbed with me when I commented about him). Also some people who have responded to me have assumed because I am female that I am a beginner or I don't know very much.

Let me be clear. I appreciate EVERYBODY on this site and I thoroughly enjoy reading the postings and going back to read past posts.

I am sorry if I came across as abrupt or offensive.

tringlomane

tringlomane

Threads: 8
Posts: 6284

Joined: Aug 25, 2012

May 24th, 2013 at 4:04:28 PM permalink

Although most things have been covered to the level I would cover them, I do have one tidbit to add.

When dealing with things like session bankrolls, it's good to remember that you will fall within 2 SDs of the mean ~95% of the time. So a -2SD result or worse will happen ~2.5% of the time. If you are someone who doesn't like to go broke earlier than expected very often, you can use this 2 SD mark to set up a fairly conservative session bankroll.

So if the table is averaging 25 points an hour (does this estimate sound good craps players?) and your just flatting the pass line at $10 with 3X odds and you want to play 2 hours, then a conservative bankroll would be (SD value from 7craps):

Expected loss = (0.0141 units lost/roll)*2hrs*25rolls/hr*$10 = $7.05

2SDs from mean = 2*(3.840744 units/roll^0.5)*sqrt(2hrs*25rolls/hr)*$10 = $543.16

Conservative bankroll (~2.2% of busting) = Expected loss + 2 SDs ~= $550

Since I am a terrible low roller, if I am playing craps, its $5 with 1X odds at the most...lol

Jimbo

Threads: 5
Posts: 158

Joined: Mar 11, 2013

May 29th, 2013 at 4:13:49 AM permalink

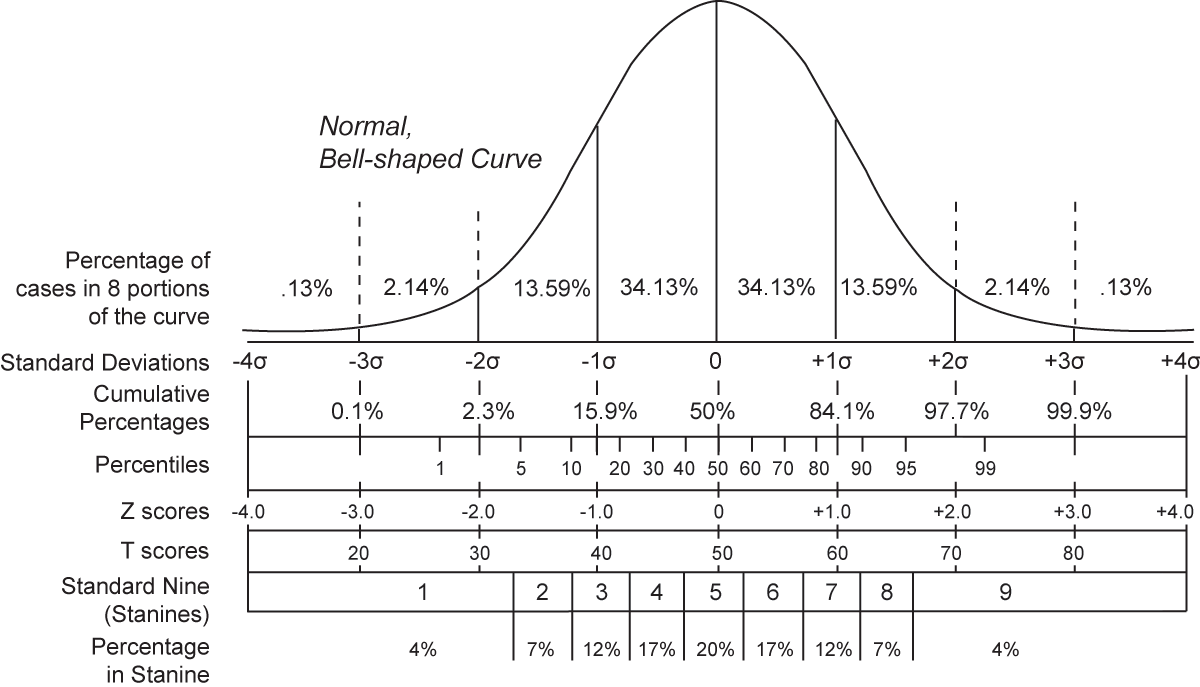
This bell curve shows the probability distribution of standard deviation. (I think I said that correctly.)

I understand in statistics, this bell curve for standard normal distribution is also referred to as the 68-95-99.7 rule or the 3-sigma rule or the empirical rule--which states that about 68.27% of the values lie within 1 standard deviation of the mean in a normal distribution. Similarly, about 95.45% of the values lie within 2 standard deviations of the mean. Nearly all (99.73%) of the values lie within 3 standard deviations of the mean.

I do not fully understand the math or the theory behind this, even after trying to grasp this from reading a couple of sources.

I know it is not necessary to know this in order to play and enjoy craps! But if someone is so inclined to explain this as simply as possible, I would be grateful.

However, this is not my main question. Rather--

I assumed the standard deviation percentages as shown on this bell curve applies to the standard deviation for any craps bet. However I was confused by the posting from MangoJ:

Quote: MangoJ
That is the meaning of standard deviation of a gaussian variate. There are several different variates, depending of the specific bet. All of them have properties called "standard deviation", and is a measure of the width of the probability distribution. But not with those numbers above....

By the way, MangoJ referenced a bell curve posted by s2dbaker. I substituted the same bell curve--only set out a little differently.

My question is this: Is it correct that the probability for a craps session outcome (or, for that matter, the session outcome for any casino game) will be within the standard deviation percentages shown by this bell curve? Or, as suggested by MangoJ, does this depends on the specific bet?

PapaChubby

PapaChubby

Threads: 11
Posts: 496

Joined: Mar 29, 2010

May 29th, 2013 at 5:02:25 AM permalink

Quote: Jimbo
My question is this: Is it correct that the probability for a craps session outcome (or, for that matter, the session outcome for any casino game) will be within the standard deviation percentages shown by this bell curve? Or, as suggested by MangoJ, does this depends on the specific bet?

No individual casino bet has a probability distribution function which resembles the bell curve.

However, the central limit theorem states that if you combine enough independent bets, the distribution function of the total will eventually resemble the bell curve, regardless of what the distribution functions of the individual events look like.

Consider a pass line bet. There are only two discrete outcomes for this bet. There's ~50% probability that you'll lose one betting unit, and ~50% probability of winning one betting unit. For two consecutive bets, there's ~50% probability of breaking even, ~25% probability of losing 2 units, and ~25% probability of winning 2 units. You might already be able to visualize the bell curve taking shape. It will probably take something like 25 bets before you get a reasonable approximation of the bell curve. The standard deviation will be about 5 units after 25 bets.

For a pass line bet with full odds, there are now more possible outcomes from a single bet. The probability distribution for a single bet is more complicated, but is still fairly well behaved. It may take 100 bets before the distibution of the total resembles the bell curve.

I'm not much of a craps guy, but I guess there's something called a fire bet (sometimes) which is a jackpot bet. The distribution function of this bet provides a very high probability of losing one betting unit, and a very, very small probability of winning a jackpot. You would need to make millions of these bets before the total distribution function would start to resemble a bell curve. You would not reach this condition during a betting session, nor during a lifetime most likely.

Jimbo

Threads: 5
Posts: 158

Joined: Mar 11, 2013

May 29th, 2013 at 6:04:55 AM permalink

Quote: PapaChubby
No individual casino bet has a probability distribution function which resembles the bell curve.

However, the central limit theorem states that if you combine enough independent bets, the distribution function of the total will eventually resemble the bell curve, regardless of what the distribution functions of the individual events look like.

Consider a pass line bet. There are only two discrete outcomes for this bet. There's ~50% probability that you'll lose one betting unit, and ~50% probability of winning one betting unit. For two consecutive bets, there's ~50% probability of breaking even, ~25% probability of losing 2 units, and ~25% probability of winning 2 units. You might already be able to visualize the bell curve taking shape. It will probably take something like 25 bets before you get a reasonable approximation of the bell curve. The standard deviation will be about 5 units after 25 bets.

I did not mean to imply that any "individual casino bet" has a probability distribution function that resembles a bell curve.

Thank you, PapaChubby, for your quick response and for explaining concisely how this bell curve comes about. It seems so logical when you explained it the way you did. Because of your posting, I also looked more at the the central limit theorem. I think I now understand better, pursuant to probability theory and the central limit theorem, that under conditions such as the throw of dice, with a well-defined mean and variance, and with sufficiently large number number of bets, the mean will be approximately normally (and identically) distributed.

I don't really know exactly the theory as to why the distribution follows the "68-95-99.7 Rule"--but I presume that is where the math functions come into play.

Consistent with your explanantion, PapaChubby, I found the following diagram showing the comparison of probability density functions, p(k), for the sum of n dice to show their convergence to a normal distribution with increasing n, in accordance with the central limit theorem.

Thanks again.

cowboy

cowboy

Threads: 6
Posts: 183

Joined: Apr 22, 2013

May 29th, 2013 at 12:00:21 PM permalink

Concerning the "68-95-99.7 Rule", we are looking at the area below the curve. As in the diagram you posted (a nice diagram BTW), you can see that 34.13 plus 34.13 % of the area below the curve is bounded by one standard deviation, either above or below the center. Likewise for the areas bounded by two or three standard deviations, i.e. ~95% and ~99% of the area.

If you have a population of samples that behave according to a bell shaped distribution, then you can expect that 68% of those samples will be found in the area of plus or minus one standard deviation from the mean - which is the center line.

Although the bell curve certainly applies to endless samples of rolling two dice, the way it applies to playing a game with a negative expectation is different. In this case the center line is the average house edge of the bets you typically make. You can expect to lose that much if everything performed "on average". But when you win overall it's because that session fell on the plus sigma side of all the samples of sessions considered. But the center line is not a break even point, it's a loss point. So more of the area of the curve falls below the break even point and less of it above.

Rather than looking at the samples in the population being playing sessions, you can look at them as being individual bets, each with their own center line at whatever the house edge for that bet is.

Jimbo

Threads: 5
Posts: 158

Joined: Mar 11, 2013

May 29th, 2013 at 1:05:30 PM permalink

You are exactly right, cowboy.

That is why--in the previous post from 7craps--in the example of 60 bets on the pass line with 0 odds--the EV is -$4.24 (which becomes your "center line" in the bell curve in that example). The standard deviation for those 60 wagers is $38.73. Which would mean that for 1 SD range, the amount is from -42.97 to $34.48 (and so forth for 2 SD and for 3 SD).

Because craps is always a negative expectation game--as you state, cowboy--it does mean that for there to be a winning session in accordance with the "68-95-99.7 Rule," you must have more than the average number of favorable bets to offset the negative EV.

MangoJ

Threads: 10
Posts: 905

Joined: Mar 12, 2011

May 29th, 2013 at 1:42:55 PM permalink

Quote: Jimbo
My question is this: Is it correct that [bell curve is] the probability for a craps session outcome ?

This depends on your "session", i.e. money management. If your session is to play a fixed (and large) number of crasp bets (or any other game), then YES your session outcome will following the bell curve.

However, if you play less bets if you lose, and play more if you win, your session outcome will be very different from a bell curve. For example, imagine the "money management" that you stop playing whenever you are at a net loss. Since you never stop at a win, your session outcome will always be negative. Then if your only betsize is 1 unit - all sessions will end with a "1 unit loss" - nothing like a bell curve thing.

cowboy

cowboy

Threads: 6
Posts: 183

Joined: Apr 22, 2013

May 29th, 2013 at 2:25:33 PM permalink

Quote: MangoJ
Quote: Jimbo
My question is this: Is it correct that [bell curve is] the probability for a craps session outcome ?

This depends on your "session", i.e. money management. If your session is to play a fixed (and large) number of crasp bets (or any other game), then YES your session outcome will following the bell curve.

However, if you play less bets if you lose, and play more if you win, your session outcome will be very different from a bell curve. For example, imagine the "money management" that you stop playing whenever you are at a net loss. Since you never stop at a win, your session outcome will always be negative. Then if your only betsize is 1 unit - all sessions will end with a "1 unit loss" - nothing like a bell curve thing.

Then the bell curve will apply to the length of your sessions.

Jimbo

Threads: 5
Posts: 158

Joined: Mar 11, 2013

May 29th, 2013 at 2:52:01 PM permalink

Quote: MangoJ
If your session is to play a fixed (and large) number of crasp bets (or any other game), then YES your session outcome will following the bell curve.

That brings up a good point.

I have mentioned before that our analysis of betting scenarios using math formulas and math principles can be accomplished provided the bets are the same amount and there are not many additional simultaneous bets to also factor in. The scenarios which have been posted as examples--and consistent with what you just posted, MangoJ--are for bets of equal or fixed amounts and generally include a sufficient number of bets. In these cases, the more the bets, the closer the end result (end of session) will coincide with the bell curve consisting of 1, 2 and 3 standard deviations.

I would add what you just stated, MangoJ, that there is a further layer of complexity when we adjust the size of our bets (to incorporate either positive or negative progressions) and/or when we adjust the length of the playing session pursuant to win goals and loss limits. I can easily see that the "session" would not coincide with the bell curve where we have altered or interfered with the betting sequence in an artificial way.

In these instances, I suppose the only way to analyze the betting scenario is with simulations (such as with WinCraps).

Quote: MangoJ
This depends on your "session"

Your comment about "sessions" brings up another interesting point, though this is probably a little off the main subject of the thread.

What is the actual length of a playing "session" from a mathematical viewpoint?

The dice have no memory (and no ears and no eyes) to know when or how long you've played. If you take a bathroom break or a dinner break, does that mean the old session ended and a new session begins upon your return? Is the playing session for the day or for the weekend? And what difference is it to the dice if you depart the casino and return in 6 months? To the dice, it is no different than if you did not take a break at all. For all the dice knows, you've never left the table.

From a mathematical perspective, are we not simply playing one long session?

The only time a session really ends is if you decide to quit playing for good and do not return to play again.

MangoJ

Threads: 10
Posts: 905

Joined: Mar 12, 2011

May 29th, 2013 at 3:15:28 PM permalink

Quote: Jimbo
What is the actual length of a playing "session" from a mathematical viewpoint?

I would see a "session" in analogy to the runtime of an algorithm. However, an algorithm (by definition) is deterministic (and thus has a fixed runtime). In this analogy, if you have some sort of "betting plan", then the session would be all play following that very plan.

The plan itself may explicitly be given by money management, bankroll constraints, stop limits - or simply time constraints or other kind of events you base your play on.

Jimbo

Threads: 5
Posts: 158

Joined: Mar 11, 2013

May 29th, 2013 at 4:01:22 PM permalink

I agree with your response about length of "session" and analysis.

My previous remarks were more philosophical. With a little bit of truth.

gr8player

gr8player

Threads: 8
Posts: 606

Joined: Mar 2, 2013

May 29th, 2013 at 4:39:35 PM permalink

Quote: Jimbo
What is the actual length of a playing "session" from a mathematical viewpoint?

The dice have no memory (and no ears and no eyes) to know when or how long you've played. If you take a bathroom break or a dinner break, does that mean the old session ended and a new session begins upon your return? Is the playing session for the day or for the weekend? And what difference is it to the dice if you depart the casino and return in 6 months? To the dice, it is no different than if you did not take a break at all. For all the dice knows, you've never left the table.

From a mathematical perspective, are we not simply playing one long session?

The only time a session really ends is if you decide to quit playing for good and do not return to play again.

Session management and money management are the very backbone of my pre-planned Bac play.

I concede that "from a mathematical perspective", each bet is affected similarly. I play Bac, which is, as we all know, a negative expectancy game.

And that very fact, IMHO, makes my pre-planned session- and money-management controls all the more important.

I'm playing "the house's" game, not my own. Hence, I'm getting the short end of the stick (read: the house edge).

In order to combat that, I need to convert the game to my own. I need to play my game. I need to control that which I can control.

If that means (oh, and, trust me on this, it does) that I need to "break up" that "one long session" into my own personal starting and stopping points, well, then, so be it.

And I happen to be of the belief that my rather strategic "breaking up" of that "one long session" is what facilitates my chances of success at this game over the long term.

I am not "the house". "The house" plays this game in "continuum"; they just keep dealing, shuffling, and dealing, over and over again. "The house" is a machine. A continuous, non-thinking, decision-spewing machine.

I, on the other hand, am human. I cannot possibly match up with their "continuum". So the long term, the "one long session", is all their's. That much I concede.

But, as human, I've a brain. I can think, and I think I know what I can and cannot control regarding this game. So I've developed a game plan built around what I can control, in order to "break up" that "one long session" into, frankly, something alot more manageable and controllable for me.

For me. For me and my psyche. For me and my bankroll. For my best interests.

That's what "session play" affords a player such as myself. It lands me in the very best position to counter their "house edge" that affects my singular bets.

I decide, at each and every separate and distinct session, the optimal stopping point based upon my current results, my current standing at the game, my current criteria. I decide. So I lump those "singular bets" into "sessions" that begin and end at the points that are most advantageous for me.

cowboy

cowboy

Threads: 6
Posts: 183

Joined: Apr 22, 2013

May 29th, 2013 at 8:01:32 PM permalink

Quote: Jimbo

In these instances, I suppose the only way to analyze the betting scenario is with simulations (such as with WinCraps).

I agree. I've written my own simulator to analyze the effect of different betting strategies. Assuming you set a starting bankroll and have target amounts for when you will leave the table (either up or down) or if those don't kick in, then leave after a certain number of hours (based on an average number of rolls per hour).

It's interesting to see what the percentage of winning and losing sessions will be based on 100,000 sessions using a certain set of criteria. So far the percentage of simulated winning sessions is between 30% and 40%, dependent on the betting strategy.

I need to revise my simulator to analyze some of the betting strategies I've read about on this forum.

The big question is that since I can never play 100,000 sessions, will my own limited number of sessions be better or worse than what the simulator predicts.

crapswoman