How many people would you expect to meet...

...before you met one born on a Wednesday?

Sounds like a question made for the Wizard but I'll take a shot. If we assume there's an even distribution of births over days of the week then you will have a 53% chance of meeting someone born on a Wednesday if you've met 5 people: 1 - (6/7)^5

A report from the CDC shows that births are significantly less common on Saturday and Sunday, most likely due to scheduled caesareans and induced labor. The birth rate they list for 1997 shows 11,723 births on Wednesdays out of 74,407 total births tracked or 15.75%. This would mean, at least for people born in 1997, that after meeting 5 people the chance that at least one was born on a Wednesday is 57%. The chance is 49.6% for 4 people. I'm sure I'm making several horrible assumptions there but I feel safe saying your answer is slightly over 4.

Not many...what doctor wants to work on a Friday or Monday, shiiit...

__6__

Care to show your work Wizard?

the old song says "wednesday's child is full of woe"...
i hope i don't meet one.

I found this problem in an old book called Problematical Recreations - 10th in a series that I picked up at a swap meet for a buck this past weekend.

The answer given is 7. The explanation given in the book is this:


Not 3.5 since this a case of sampling with replacement.

Each person has a 1/7 probability of having been born on a Wednesday. In a sense then, each person is "1/7 of an expected Wednesday child." Since it requires 7 such to add up to a Wednesday child, the answer is 7 people.


I initially thought, for a moment, the answer was 3.5. But based upon some of the not-so-obvious answers to some of the other questions in the book, I decided 3.5 was probably not correct.

This afternoon I wrote a computer program to simulate this problem (10,000,000 trials) and I decided the answer was indeed 7. (A total of 70,015,454 people were "met" in all, giving the average number of people met for each trial to be 7.0015)

Once I refreshed memory on what the differences were between "sampling with replacement" and "sampling without replacement" I realized the answer could not be 3.5 or 4 or even 5 point something. I tweaked my program to let me know how many people the "unluckiest" person had to meet before he met someone born on a Wednesday. The answer for one 10,000,000 trial was 100 (!) and for a later trial it was 108!

In a case of sampling WITHOUT replacement, if I understand the differences, the correct answer would be 4. (1+2+3+4+5+6+7) / 7 = 4

I'm with the Wizard on this one. Ed, maybe you included the Wednesday guy that you met. There should only be 6 people that you meet BEFORE the Wednesday guy. Otherwise, you met 7 other people for every Wednesday guy, so his frequency is only 1/8.

Quote: EdCollins

...The answer given is 7...

7 is the answer to this slightly different question: How many people would you expect to meet in order to meet one born on a Wednesday?

Yes, I think this could be back to a matter of language, which often seems to cause us difficulty. My limited analysis suggests that the answer is 7 if you interpret the question to mean you should include the person born on Wednesday in your count. If you are only to include those you meet before you meet that person, I think the answer is 6, which agrees with the Wizard's answer.

My formula (for not counting the person born on Wednesday) is:



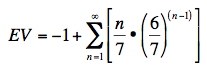
I suspect there is a way to simplify that, but my brain is too atrophied to do it. I just used Excel to figure the first 60 terms and got EV=5.9926. I suspect that if I included all ∞ terms, it would come out to 6. If you leave off the -1, you include the person born on Wednesday and get a total of 7.

Ah! I think that's it. I agree with Crystal and Chester and Doc's post about interpreting the question properly. Excellent work.

Quote: PopCan

If we assume there's an even distribution of births over days of the week then you will have a 53% chance of meeting someone born on a Wednesday if you've met 5 people: 1 - (6/7)^5

Ouch. Where did I go horribly wrong on this? I figured that you'd "win" if you met someone born on Wednesday so I tried to figure out the average number of consecutive losses.

Quote: PopCan

Ouch. Where did I go horribly wrong on this? I figured that you'd "win" if you met someone born on Wednesday so I tried to figure out the average number of consecutive losses.

I think what you calculated there is the probability that you will meet the first "Wednesday" person at some point before having met four people born on other days. That is a different issue than the "expected" number of people you will meet before meeting someone born on Wednesday. You need to calculate the expected value of the number of people you will meet.

The formula I presented calculates the Expected Value of the number of people met including the Wednesday person and subtracts 1.

EV(excluding) = -1 + EV(including) = -1 + 1*P(1) + 2*P(2) + 3*P(3) + ... + n*P(n) + ...

I don't think the answer is 6.

Consider a number from 1 to 7. If you knew that the sequence of numbers is 1,2,3,4,5,6,7, then the answer would be six. But the sequence of numbers can be any combination. Therefore, the answer is 3.

I'm thinking of a number between 1 and 7. What is the number of guesses it will take before you get it right? It won't be 7 guesses? It will be 4.

Oh yeah, the replacement thing! I'm wrong.

The answer is 6.

So this reminds me of that birthday problem. I think that states: How many people do you need to have in a room for there to be a 95% chance at least two share a birthday, and its a surprisingly low answer, like 29 right?

This doesn't seem much different. If I asked "How many people do I need in a room to have better than a 95% chance two were born on the same day of the week?" that would be more like 5 right?

Now that I'm thinking through it, this problem is quite different than the sharing birth DATE problem.

Here is my solution.

Let x be the answer. x has a memory-less property, in which no matter how many people you meet, you're never overdue to meet someone born on a Wednesday. So, when you meet the first person there is a 1/7 chance he was born on Wednesday, so you would have met 0 before him. There is a 6/7 chance he was not born on a Wednesday, so you met one person and you can still expect to meet x more. So the equation is:

x=(6/7)*(1+x) + (1/7)*0
x=(6/7)*(1+x)
7x=6*(1+x)
7x=6+6x
x=6

Note that I'm assuming a 1/7 chance of being born on a Wednesday. If the probability for being born on Wednesday is w, then the answer would be (1-w)/w.

As was discussed on an earlier thread, births are not evenly distributed over days of the week. I think Tuesdays and Wednesdays were the heaviest days.

I know that's sort of not the point of the question, but I wanted to bring it up.

I "conditionally" agree with the Wiz.

If you take into account the CDC's report that there are more people born mid-week than on weekends, etc. then the answer is slightly less than 6. For the point of argument though, the correct answer is 6.



But let me see if I can cut thru the remaining clutter.

If you shuffled a deck of cards and started flipping cards, how many cards can you expect to flip before flipping the [specific card] ?

Did you say 26? Good! (Note, the answer could be 25, or 25.5 depending on how anal you are about the math and phrasing.)

What about if you shuffled the deck, flipped one card, and put it back and reshuffled? How many times would you expect to do that before flipping the desired card?

Did you say 52? Great. (or 51 if you're anal.)

That's the difference between "sampling without replacement" and "sampling with replacement"

In the case of birthdays, with 7 billion people on this planet, although we may be careful not to ask the same person twice, the pool size is large enough that the math works by "sampling with replacement".

With this type of question, the answer is always the number of possibilities. Or minus 1 depending on the wording.

Quote: ewjones080

So this reminds me of that birthday problem. I think that states: How many people do you need to have in a room for there to be a 95% chance at least two share a birthday, and its a surprisingly low answer, like 29 right?

The reason this number is so low is because you're comparing each new response, to every response alreay provided, so the number of combinations increases exponentially with each person added to the pool.


Here's another way to look at things.

If you started asking people their birthday (month and day), how many people would you expect to ask before you get a response that is the same as the previous person's response?

The answer is 365.25

Quote: Doc

I think what you calculated there is the probability that you will meet the first "Wednesday" person at some point before having met four people born on other days. That is a different issue than the "expected" number of people you will meet before meeting someone born on Wednesday. You need to calculate the expected value of the number of people you will meet.

The formula I presented calculates the Expected Value of the number of people met including the Wednesday person and subtracts 1.

EV(excluding) = -1 + EV(including) = -1 + 1*P(1) + 2*P(2) + 3*P(3) + ... + n*P(n) + ...

Thanks. The moment you said "Expected Value" it made sense.

Quote: Wizard

Note that I'm assuming a 1/7 chance of being born on a Wednesday. If the probability for being born on Wednesday is w, then the answer would be (1-w)/w.

I was going to bring that up. Is there any kind of data of the weekday distribution of births? Did you run across any in your actuarial work?

US data for 2006. Please note: this chart does NOT show trends by year.

Average for all days: 11,686.

Monday: 12,079
Tuesday: 13,397
Wendesday: 13,482
Thursday: 13,444
Friday: 13,151
Saturday: 8,745
Sunday: 7,587

So yeah, the number of people is less than 6. Closer to 5.

Wow.

I hadn't realized that the numbers were skewed that far away from weekends.

And what's going on on Monday? Is that golf day?

---

But I'd stand by my prior statement that, ignoring the census data, for point of argument, the answer is 6.

Then again, since the Wiz is a former census worker, should we really ignore the census data? ;)

Quote: boymimbo

US data for 2006. Please note: this chart does NOT show trends by year.

Thanks.

I don't know if we can assume 06 to be a typical year or not, or whether even there are trends over the years or not.

The exact length of a pregnancy can't be known. But there are ways to induce labor, and there are C-sections. My sister in law, for example, after delivering her first child by C-section after hours of labor, scheduled like procedures for her other two children. Naturally those two were born on weekdays.

I think there are also ways of delaying labor (which would be useful to prevent premature births). But I'm on shaky ground on that.