Recommended online casinos

Thread Rating:

BruceZ
BruceZ
BruceZ
  • Threads: 2
  • Posts: 57
Joined: May 23, 2015
July 27th, 2015 at 6:30:43 AM permalink
Quote: mustangsally

thank you again
there is a trick (well known) for this when p=1/2
for Heads or Tails run

it is from a famous paper too
Mark F. Schilling
"The Longest Run of Heads"

I wonder if the Wizard knows him personally... (SoCal boys)


That follows directly from the trick I showed earlier for a fair coin whereby

P(run of at least m heads or tails in n tosses) = P(run of at least m-1 heads in n-1 tosses)

since we need m-1 "no-changes" in n-1 tosses where the no-changes have probability 1/2 same as heads. Then

P(m is longest streak of heads or tails in n tosses) =
P(run of at least m heads or tails in n tosses) - P(run of least m+1 heads or tails in n tosses)

= P(at least m-1 heads in n-1 tosses) - P(at least m heads in n-1 tosses)

= P(m-1 is longest streak of heads in n-1 tosses).
mustangsally
mustangsally
mustangsally
  • Threads: 25
  • Posts: 2463
Joined: Mar 29, 2011
July 30th, 2015 at 10:53:19 AM permalink
as a summary to this correction thread
here is some info:
remember p =1/2

H(7+run) = 0.317520387
T(7+run) = 0.317520387

https://www.wolframalpha.com/input/?i=streak+of+7+successes+in+100+trials
6289139215543317778531752497 / 19807040628566084398385987584
~~0.31752

either H or T = 0.542336855

https://www.wolframalpha.com/input/?i=streak+of+6+successes+in+99+trials
171873410099752056462360779295 / 316912650057057350374175801344
~~0.542337

this is new...
both H AND T = 0.092703919
H + T - (either)
0.635040774 - 0.542336855 = 0.09270392
=============================================
and because the Wizard threw this one in...
H run = 7 (exactly length 7) = 0.172920892
T run = 7 (exactly length 7) = 0.172920892
either H or T = 7 = 0.318273134
both H AND T = 7 = 0.02756865
=============================================
now a new slot machine at Sally's Casino is this
*7 Streak*
one can bet from $1 to $100 that in 100 coin flips
(fair, done on a computer screen of course) the bet wins if at least one Heads AND at least one Tails streaks are at least 7 in length)

a winning bet pays 9 to 1
(the high limit machine from $100 to $1000 the winning bet pays 9.5 to 1)

and sure, bet against that event too
bet $10 to win $1 (or $100 to win $10 etc) that the event does not happen (Both H and T streak 7 or higher)

there are many other bets also available and one can make more than one, just like when playing Roulette

all 7 machines are always busy and lots of yelling and screaming and W2Gs...
so i guess they are having fun, like when playing video Keno!
i hope i am making money from these machines

Mully
I Heart Vi Hart
mustangsally
mustangsally
mustangsally
  • Threads: 25
  • Posts: 2463
Joined: Mar 29, 2011
July 30th, 2015 at 11:18:31 AM permalink
Quote: BruceZ

That follows directly from the trick I showed earlier for a fair coin whereby <snip>

another trick that many may not know
i think this is from Mark S but could not locate the words

double the number of flips
and the probability is about the same for run+1

halve the number of flips and the probability is about the same for run-1

example with the streak of at least 7
it shows in a table i made

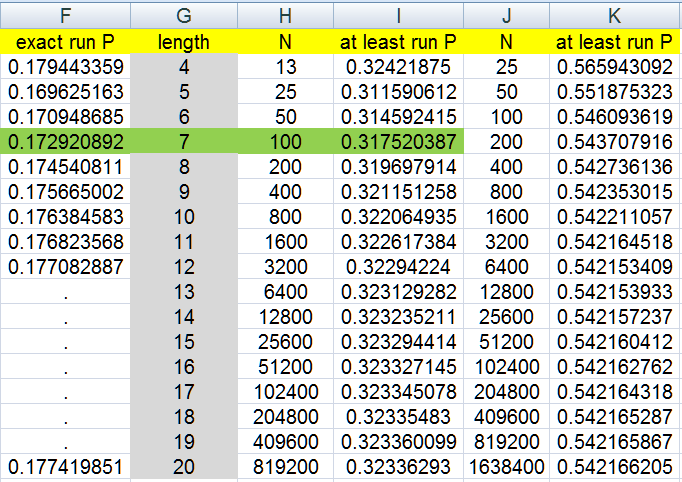
at least 7 in a row at 100 flips
is about the same as

at least 8 in a row at 200 flips
is about the same as

at least 6 in a row at 50 flips

i like stuff like this

happy reading and coin flipping!
Sally

wow
the Angels OVER was a nail biter last night
thank you Albert!
I need another vacation real soon
I Heart Vi Hart
mustangsally
mustangsally
mustangsally
  • Threads: 25
  • Posts: 2463
Joined: Mar 29, 2011
September 28th, 2018 at 9:24:55 PM permalink
Quote: pacomartin

However, there is a closed form expression using k-step Fibonacci sequences, where the standard Fibonacci sequence is defined as a 2 step Fibonacci sequence.
The extension of the concept is natural.
But there are two problems,
(1) the calculation is unstable for large numbers,
(2) Fibonacci sequences are calculated recursively, so there is no avoiding the recursion.
Mark Nelson describes the solution in his column , but he got it from the online guide to Mathematica here .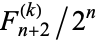

I was told that there is an incomplete answer here, and I just found it.

the Fibonacci formula shown above is for
NO runs of length X in N trials.
so one would have to subtract that calculated value from 1 to find the probability of at least one such streak.

One easily get an exact value using say Pari/GP
for example (a free windows program and there is a page online to run code too)
exact answer:
6289139215543317778531752497 / 19807040628566084398385987584
in decimal form
0.31752038749660580748723704512132355489

the 102nd 7th step Fibonacci number is
865145690433457063670671045568
some gp code
run=7
 trials=100
 gen(n)=k->my(v=vector(k,a,1));for(a=3,min(k,n),v[a]=2^(a-2));for(a=n+1,k,v[a]=sum(j=a-n,a-1,v
));v
 for(n=run,run,print(n"\t"gen(n)(trials+2)))
 a=865145690433457063670671045568; \\the 102nd 7th step Fibo number
 b=2.^100;
d=1 - a/b
print(d)

of course a simple transition matrix solves this real fast and easy too
that already has been shown

here is some R code for that
using section 1r.
https://sites.google.com/view/krapstuff/home
> runs.r(7,100,0.5,0)
[1] "for a run of 7, success probability: 0.3175203875"
[1] "1 in: 3.1494"
[1] "Number of trials: 100"


hope this can add to our interest in streak probabilities.
Sally
Last edited by: mustangsally on Sep 28, 2018
I Heart Vi Hart
smoothgrh
smoothgrh
smoothgrh
  • Threads: 91
  • Posts: 1605
Joined: Oct 26, 2011
September 28th, 2018 at 11:33:22 PM permalink
Quote: mustangsally



the Fibonacci formula shown above is for
NO runs of length X in N trials.
so one would have to subtract that calculated value from 1 to find the probability of at least one such streak.



I am primordial soup stewing among gods.
7craps
7craps
7craps
  • Threads: 18
  • Posts: 1977
Joined: Jan 23, 2010
April 25th, 2019 at 11:50:17 AM permalink
Quote: pacomartin

But there are two problems,
(1) the calculation is unstable for large numbers,
(2) Fibonacci sequences are calculated recursively, so there is no avoiding the recursion.

using an online calculator as pari/gp or even wolfram alpha
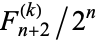
(1) and (2) are now deemed not problems.

(2) Fibonacci sequences are calculated recursively, so there is no avoiding the recursion.
(2) is true but one can use a simple matrix in a program that can raise that matrix to any arbitrary power.

I just finished some pari/gp code and thought I would add it to the mix.

the matrix solution for any n-step Fibonacci number can be found here in this pdf:
http://maths.dur.ac.uk/~dma0rcj/PED/fib.pdf

online pari/gp calculator found here: (works fast for me)
https://pari.math.u-bordeaux.fr/gp.html
the code below uses a matrix solution
run=7; \\nStep
trials=100; \\nStep Fibonacci number
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
numberRun=trials+2; \\nStep Fibonacci number+2
col=run;
\\build and populate matrix
A=matrix(run,col);
r1=vector(run,i,1);
A[1,]=r1;
for(i=2,run,A[i,(i - 1)]=1); \\diagonal starts at A[2,1]
result=A^numberRun;
fibNumber=result[1,run];
print(fibNumber)\\for run : optional, can be commented out
\\\\\\\\\\
x=1-(fibNumber/2^trials);
print(x)
xDec=1.*x;
print(xDec)
## \\time
#digits(fibNumber)


printed results:
865145690433457063670671045568 <<<< 102nd 7th step Fibonacci number
exact result:
6289139215543317778531752497/19807040628566084398385987584
as decimal:
0.3175203874966058074872370451

all in agreement with another pari/gp solution and result

enjoy

I did this as a question was asked years ago in 2+2 forum for the chance of a run of at least 10 Heads in a row in 1000 fair coin flips.
member BruceZ had this to say
"The exact formula in this case is
1 - F10[1002]/2^1000
where F10[1002] is the 1002nd Fibonacci 10-step number.
Whether you use this formula, or the one from the perl script above, the answer is exact, and you will need a program or spreadsheet either way, unless you just happen to know the first 1002 Fibonacci 10-step numbers."
https://forumserver.twoplustwo.com/25/probability/successes-row-904091/

here is pari/gp code (less than 1 sec on my internet connection)
? run=10; \\nStep
trials=1000; \\nStep Fibonacci number
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
numberRun=trials+2; \\nStep Fibonacci number+2
col=run;
\\build and populate matrix
A=matrix(run,col);
r1=vector(run,i,1);
A[1,]=r1;
for(i=2,run,A[i,(i - 1)]=1); \\diagonal starts at A[2,1]
result=A^numberRun;
fibNumber=result[1,run];
print(fibNumber)\\for run
\\\\\\\\\\
x=1-(fibNumber/2^trials);
print(x)
xDec=1.*x;
print(xDec)


6584958798384775410989568667391064982626093779379678589423888296935429803281664819022559936019379343684500202235918204744347504028936246904338337417504701896318926607869016202348627459568889551267118109653819261878460946269507218690144892367948689821935916413582143326098056502752519556568695574716415
4130127273477897798494681823208953122987954337675657485013615586768080707967696405909423852137579237591446526939613263507523948827986893531646240157193872907615641166955214783072447145493481590610836072499227213105120994997891548869020651578128373092635280064104398841562373328900104830268510093352961/10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376
0.3854497524124816359103324432
line 1 above is the 1002nd Fibonacci 10-step number
Last edited by: 7craps on Apr 25, 2019
winsome johnny (not Win some johnny)
RSS Feed
  • Jump to: