How to figure odds of losing "x" hands in a row.
1. What are the odds of losing 4,5, and 6 hands of BJ in a row?
2. What are the odds of losing 4,5 and 6 pass/don't pass bets in craps in a row?
3. If I know the probability of a win (say 48%) how do I figure this for 4,5,6 or for that matter any number of trials in a row?
Of course, with BJ, it's complex because of pushes, splits and doubles.
But if the assumption is you'll lose 52% of the time, then 52& ^ 4 = 7.3%, 52% ^ 6 = 1.9%, etc.
Quote: DJTeddyBearSimple: It's just the odds of one occurrence to the power of the number of occurrences you're concerned with.
Of course, with BJ, it's complex because of pushes, splits and doubles.
But if the assumption is you'll lose 52% of the time, then 52& ^ 4 = 7.3%, 52% ^ 6 = 1.9%, etc.
I thought that was it but it seemed too simple.
Quote: AZDuffmanI thought that was it but it seemed too simple.
And the answer is for only when n=4 or for 4 trials.
The next question to follow should be (using the blackjack lose rate): Probability of losing 4 hands in a row in 5 trials? How about 10 trials?
The math of streaks is a very challenging quest when p is NOT equal to .5, like in a fair coin toss, and all the recursive, matrices, Fibonacci number formulas that all deal with a fair coin toss probability will not help us in finding an exact answer for a biased coin toss.
BruceZ at http://forumserver.twoplustwo.com/25/probability/successes-row-904091/ has a perl script to calculate the chance of at least a run in n trials.
Better yet,
He repaired an online calculator using javascript that can be found HERE that a friend of mine placed in a html page, and it is 100% accurate up to n=1,000,000 (that is as high as I have tested). BruceZ (IMHO) is a rare math genius good guy that does a great job on explaining how to do something.
Probability of losing lose 4 BJ hands in a row in 5 trials? 10.82119168%
How about 10 trials? 27.7326854715615%
How about 100 trials? 98.4214302644146%
How about a ML Baseball team that has a 50% win rate, in 162 games how about a win streak of 5 or more? 93.4519474125220%
6 or more? 72.7712414312032%
How about a ML Baseball team that has a 60% win rate,(the best teams) in 162 games how about a win streak of 5 or more? 99.7768554358947%
6 or more? 96.6318323647770%
A calculator or script is a very useful tool. It saves time so computer simulations are not needed.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Soon to be in a new thread
But the streaks that are calculated are an "at least 1" calculation.
At least 1 streak of 5 or more in 162 games.
I am working on the math to solve the below question.
What about 2 streaks or more?
3 streaks or more? n streaks or more.
Example. a fair coin toss. n=10. Probability of at least 1 run of 2 or more heads is exactly 880/1024 or 85.9375%
Formula is 1-F2[12]/2^10 where F2[12] is the 12th Fibonacci 2-step number. (144)
Probability of at least 2 runs of heads 2 or more in 10 flips.
Answer 368/1024 or 0.359375
I have no formula for the answer, yet. Just crunched the numbers in Excel after placing all possible sequences (2^10) in lexicographical order.
A photo of my Excel sheet is HERE so one can see what i am trying to explain.
It is a great exercise in math and when I get enough information on it I will post a new thread about it.
Probability of at least 2 runs of heads 3 or more in 10 flips.
Answer 56/1024 or 0.0546875
Probability of at least 2 runs of heads 4 or more in 10 flips.
Answer 5/1024 or 0.0048828125
Probability of at least 2 runs of heads 5 or more in 10 flips.
Answer 0/1024
Need at least 11 flips for it to happen once.
Quote: nope27...He repaired an online calculator using javascript that can be found HERE that a friend of mine placed in a html page, and it is 100% accurate ...
I'm not sure what your point is, but using that calculator, I got the exact same results, albeit not rounded, as I reported in my post above.
PS:
>3. If I know the probability of a win (say 48%) how do I figure this
1 minus .48 is .52, in case that went past anybody
Quote: DJTeddyBear
I'm not sure what your point is, but using that calculator, I got the exact same results, albeit not rounded, as I reported in my post above.
I was not questioning your math. You are 100% correct. 4 BJ losses in a row in 4 hands. .52^4
But it is for only 4 hands.
How about at least 4 losses in a row in 10 hands?
20 hands?
100 hands?
It is just more complex math.
Streaks (or runs), either win or lose, exist.
The more trials, the longer the streaks, win and lose.
More trials, more streaks.
Quote: nope27I was not questioning your math. You are 100% correct. 4 BJ losses in a row in 4 hands. .52^4
But it is for only 4 hands.
How about 4 losses in a row in 10 hands?
20 hands?
100 hands?
It is just more complex math.
Streaks (or runs), either win or lose, exist.
The more trials, the longer the streaks, win and lose.
More trials, more streaks.
This calculator will raise things to the power of x quite nicely for very large numbers of trials; I like it anyway
http://web2.0calc.com/
Quote: nope27I was not questioning your math. You are 100% correct. 4 BJ losses in a row in 4 hands. .52^4
But it is for only 4 hands.
How about at least 4 losses in a row in 10 hands?
20 hands?
100 hands?
It is just more complex math.
Streaks (or runs), either win or lose, exist.
The more trials, the longer the streaks, win and lose.
More trials, more streaks.
What I see is the probability of getting exactly 4 losses in a row in 4 hands is .52^4 just like DJ posted or a binomial distribution formula will also work.
The probability of getting at least 1 run of 4 losses or more in a row in 10 trials is 27.7326854715615% using the streak calculator.
How about getting a run of exactly 4 losses in a row in 10 trials?
It is a different question and should have a different answer.
A quick 1 million, 10 flip sim shows
0 849208 84.92% for NO exact run of 4
1 147086 14.71%
2 3706 0.37%
What this does not show are the runs of 5,6,7,8,9 and 10.
So I guess if a gambler "fears" a losing streak of exactly 4 in a row, he better also fear the streaks of 4 "or more" in a row.
Quote: AZDuffmanThis may seem very elementry, but it has been a lifetime since Prob/Stat class.
2. What are the odds of losing 4,5 and 6 pass/don't pass bets in craps in a row?
For the pass line:
losing 4 in a row in 4 trials 251/495^4 = 6.6111%
Taking it further...
losing 4 in a row or more, at least once, in 10 trials = 25.6268663234987%
losing 4 in a row or more, at least once, in 30 trials (hour at the craps table average)= 65.7730718927031%
losing 4 in a row or more, at least once, in 100 trials = 97.7367454127325%
So, Nope27 question, for another thread, is
losing 4 in a row or more, at least twice, in 100 trials
losing 4 in a row or more, at least 3 times, in 100 trials
I got it now. Yes, some interesting math.
Nope27, how did you arrange your 10 coin flips in lexicographical order? I had to look that one up.
Do you have VBA or a software for it?
You are then trying to calculate the probability of multiple k-streaks within n-trials.
Interesting concept.
So playing Craps for 3 hours, how many runs of losses of 4 or more, at least twice, can one expect? Simulations would provide an accurate answer.
Quote: nope27And the answer is for only when n=4 or for 4 trials.
The next question to follow should be (using the blackjack lose rate): Probability of losing 4 hands in a row in 5 trials? How about 10 trials?
Probability of losing lose 4 BJ hands in a row in 5 trials? 10.82119168%
How about 10 trials? 27.7326854715615%
How about 100 trials? 98.4214302644146%
The answer might also depend on how you deal with unfinished streaks. If in the 10 trials example you lose the last three hands, do you make 11th trial to determine if the 4 losses in a row occurs or not? You could just end at 10th trial and determine that 4 losses in a row didn't occur. But shouldn't you then only include the first 7 trials as the last streak of 3 losses is still unfinished. In another words after 7th trial you already know that 4 losses in a row cannot happen so why even make the last three trials.
But most people are not really interested in that question. They are more interested in what is the probability that they will lose 6 in a row out of an afternoon of play which may be 200-400 games. The mathematics is much different and much more complex. It can't be calculated with an algebraic formula. You need a Markov transition matrix, or the equivalent series of recursively defined algorithms.
In the case of no house edge (coin tossing) you can solve the problem with an extended definition of Fibonacci sequences called the Fibonacci-k step function.
I wrote a short paper that does not give the algorithm, but it does give some graphs for coin tossing. In some ways the graphs are better than a java script calculator, because they make it much easier to see the changes that occur as you change some parameters (double the streak length, or double the space of total games). I did two charts, one has a logarithmic scale to show a larger range of parameters.
The paper has an anecdote that you may find interesting.
====================
If you are interested in repeating the calculations for yourself you must first define a n-step Fibonacci sequence
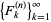is defined by letting 
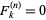for k<=0, and 
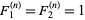, , and other terms according to the following linear recurrence sequence.
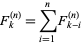for k>2.Once you have defined this function the probability that no k consecutive tails will occur in n tosses is given by
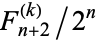where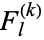 
is a Fibonacci k-step number defined above.====================
Once you know the probability that no k consecutive tails will occur in n tosses then the probability that it will happen is 100%-(not happen). There is a modification of this formula that can be defined to account for a house edge.
Quote: pacomartin
Once you know the probability that no k consecutive tails will occur in n tosses then the probability that it will happen is 100%-(not happen). There is a modification of this formula that can be defined to account for a house edge.
That was it. It was your study that got me into Fibonacci k-step numbers a while back ago. Yes, I have duplicated your work in Excel and enjoyed the learning experience. Thank you for a great effort.
Yes, the math for a fair coin is straight forward, more difficult for a biased coin for runs of at least 1.
My studies, I have completed many computer simulations also, are now to solve for multiple runs in n trials. Or runs of at least 2 etc.
Example: Playing Craps, Making 136 pass line bets, 4hours of play on average, a run of 4 wins or more in a row, at least 1 time, is 99.0750063212270% (by simulation 0.992)
a run of 4 wins or more in a row, at least 2 times, is 0.9435 (by simulation) at least 2 times meaning they do NOT overlap, they are separate runs.
a run of 4 wins or more in a row, at least 3 times, is 0.8097 (by simulation)
a run of 4 wins or more in a row, at least 4 times, is 0.6065 (by simulation)
a run of 4 wins or more in a row, at least 5 times, is 0.3745 (by simulation)
losing or winning 4 in a row or more, at least twice, in 100 trials
losing or winning 4 in a row or more, at least 3 times, in 100 trials
losing or winning 25 in a row or more, at least 4 times, in 100 trials can not happen.
As soon as I simplify some of my work in Excel I will share and maybe we can find a solution.
Quote: guido111I got it now. Yes, some interesting math.
Nope27, how did you arrange your 10 coin flips in lexicographical order? I had to look that one up.
Do you have VBA or a software for it?
You are then trying to calculate the probability of multiple k-streaks within n-trials.
Interesting concept.
So playing Craps for 3 hours, how many runs of losses of 4 or more, at least twice, can one expect? Simulations would provide an accurate answer.
Yes, I have done many, many simulations to create tables of probabilities.
It would be nice to just have a script or a formula to work with. Saves time.
lexicographical order?
I use PermuteCombine.exe
at http://saliu.com/free-science.html
It costs $10 if I remember correctly, but that gives you access to all sorts of software.
Ion Saliu is a unique person. Maybe because he is from Eastern Europe, I do not know. I am from Western Europe.
He has nice software programs but he must be slightly crazy IMO.
A relative/cumulative frequency table that can be made from data he has given a name of FFG. You can read about it there if you so desire.
Let me know if you plan to investigate the math, as you say, of multiple k-streaks in n-trials.
I have more work to do before I can share my data.
yesQuote: DeMangoI've got a craps question. If one places the 6 & 8, the odds are .375 on no hits before the 7 right?
6/16 = .375
yesQuote: DeMangoWhat are the odds of that happening 10 times in a row. Would that be .375^10?
and that would be the odds of it happening in exactly 10 rolls.
Quote: DeMangoHow about 10 in a row occurances in 480 rolls? It seems the result of 1.6% seems a little high according to nope27's friends calculator.
Remember the calculator is for 10 in a row or more, at least 1 time in 480 rolls.
My simulations show in 10,000 sessions a run of 10 or more at least 1 time occurred 156 times or 1.56%, so simulation shows the calculator numbers to be correct.
Also, since I have more info on the 6&8 win streaks B4 the 7,
in 432 rolls, (I know a weird number, I used 108 rolls per hour)
a run of 5 or more 6or8s before a 7 at least 1 time is 99.9999997386106% (sim 99.97%)
a run of 5 or more 6or8s before a 7 at least 2 times is (sim 99.79%)
a run of 5 or more 6or8s before a 7 at least 3 times is (sim 98.54%)
a run of 5 or more 6or8s before a 7 at least 4 times is (sim 94.85%)
a run of 5 or more 6or8s before a 7 at least 5 times is (sim 86.69%)
The expected value of the wait time of each run is also interesting. There is a formula for that but I will show that information with simulation results in another post.
Good point. Answer. No. The probability is based from n=10. I am dealing with a sequence of 10 hands before the first one is played as the probabilities do change as the sequence is played out.Quote: Jufo81The answer might also depend on how you deal with unfinished streaks. If in the 10 trials example you lose the last three hands, do you make 11th trial to determine if the 4 losses in a row occurs or not?
You are correct. That is all I am calculating. 4 or more.Quote: Jufo81You could just end at 10th trial and determine that 4 losses in a row didn't occur.
Again, I am only calculating the probability of a run of at least a certain length happening in n trials before it is played out. That is what probability is all about.Quote: Jufo81But shouldn't you then only include the first 7 trials as the last streak of 3 losses is still unfinished. In another words after 7th trial you already know that 4 losses in a row cannot happen so why even make the last three trials.
Quote: nope27
Remember the calculator is for 10 in a row or more, at least 1 time in 480 rolls.
My simulations show in 10,000 sessions a run of 10 or more at least 1 time occurred 156 times or 1.56%, so simulation shows the calculator numbers to be correct.
Also, since I have more info on the 6&8 win streaks B4 the 7,
in 432 rolls, (I know a weird number, I used 108 rolls per hour)
a run of 5 or more 6or8s before a 7 at least 1 time is 99.9999997386106% (sim 99.97%)
a run of 5 or more 6or8s before a 7 at least 2 times is (sim 99.79%)
a run of 5 or more 6or8s before a 7 at least 3 times is (sim 98.54%)
a run of 5 or more 6or8s before a 7 at least 4 times is (sim 94.85%)
a run of 5 or more 6or8s before a 7 at least 5 times is (sim 86.69%)
The expected value of the wait time of each run is also interesting. There is a formula for that but I will show that information with simulation results in another post.
I am understanding what you are doing.
This "wait time" that you talk about.
While the probability of an event happening(or frequency) describes how often a pattern occurs,
the waiting time describes when a pattern will occur on average from the time at which monitoring begins. This is from a book I have.
since 1/p is the expected value of an independent trial, I must conclude that a "run" is not an independent event.
Your 10 flip coin toss example, all 1024 sequences have the same frequency of 1 in 1024. So in 1024 coin flips, HHHHHHHHHH and HHTHTTTHTH have exactly the same probability of occurring. One has a run of 10 heads, the other just 1 run of 2 heads. But we know there are many other sequences that can give us a run of 2 heads and no other to give us a run of 10 heads.
Is the wait time for HHHHHHHHHH more than HHTHTTTHTH? If it is, then the only reason must be because of variance.
Can you direct me to more reading on the subject? I come up blank in Google.
Quote: guido111
Is the wait time for HHHHHHHHHH more than HHTHTTTHTH? If it is, then the only reason must be because of variance.
Can you direct me to more reading on the subject? I come up blank in Google.
This has to do with the subject of the Gambler's Fallacy and the Hot Hand belief.
http://journal.sjdm.org/10/91117/jdm91117.pdf
is one that I have studied about frequencies and wait times of runs. They use a 4 coin flip example.
One does not need to know everything about frequencies and wait times for runs, it is nice if you do know it, better to be able to use the knowledge in determining probabilities.
Good Luck
Quote: nope27
My simulations show in 10,000 sessions a run of 10 or more at least 1 time occurred 156 times or 1.56%, so simulation shows the calculator numbers to be correct.
Also, since I have more info on the 6&8 win streaks B4 the 7,
in 432 rolls, (I know a weird number, I used 108 rolls per hour)
a run of 5 or more 6or8s before a 7 at least 1 time is 99.9999997386106% (sim 99.97%)
a run of 5 or more 6or8s before a 7 at least 2 times is (sim 99.79%)
a run of 5 or more 6or8s before a 7 at least 3 times is (sim 98.54%)
a run of 5 or more 6or8s before a 7 at least 4 times is (sim 94.85%)
a run of 5 or more 6or8s before a 7 at least 5 times is (sim 86.69%)
The expected value of the wait time of each run is also interesting. There is a formula for that but I will show that information with simulation results in another post.
My simulations at first showed even higher run percentages for the 6&8 place bets. I figured it must have been due to the fact I had my place bets off on the come out roll. Your results matched mine for having the place bets always working in my last sims.
So the previous post about a 10 loss in a row on the place 6&8 was when they were working all the time.
I will finish all my sims and post my results.
1. I understand you are looking for a formula to calculate multiple k-streaks in n-trials. That is fine and dandy.
2. Any practical use?
Betting for streaks can get very expensive and unless the streaks are long, flat betting most times out performs any positive progression. Of course if you hit 10 6s and 8s in a row and press your bets each time and take them down before you lose you can win a bundle.
Just asking.
Thanks for the pdf. Wild stuff on runs.
Quote: nope27Good point. Answer. No. The probability is based from n=10. I am dealing with a sequence of 10 hands before the first one is played as the probabilities do change as the sequence is played out.
Again, I am only calculating the probability of a run of at least a certain length happening in n trials before it is played out. That is what probability is all about.
That's one way of calculating the streaks but I might also consider playing the very last streak to the end, so if in say 10 trials the last streak is still not finished, I would play it to the end because otherwise the outcome of the last streak is left undetermined. I also noted that this way the mathematics of streaks becomes simpler. The streak cut-off effect is somewhat responsible for the tricky maths I think.
Quote: guido111My simulations at first showed even higher run percentages for the 6&8 place bets. I figured it must have been due to the fact I had my place bets off on the come out roll. Your results matched mine for having the place bets always working in my last sims.
So the previous post about a 10 loss in a row on the place 6&8 was when they were working all the time.
I will finish all my sims and post my results.
1. I understand you are looking for a formula to calculate multiple k-streaks in n-trials. That is fine and dandy.
2. Any practical use?
Betting for streaks can get very expensive and unless the streaks are long, flat betting most times out performs any positive progression. Of course if you hit 10 6s and 8s in a row and press your bets each time and take them down before you lose you can win a bundle.
Just asking.
Thanks for the pdf. Wild stuff on runs.
You are welcome.
Answer to you first question is yes. I just want a formula or script. That is all.
Question 2 is also yes, but I would need more time to show my reasons.
Also your simulations above you must be careful in evaluating craps bets that resolve on 1 roll and those that resolve on 1 or more rolls.
With place bets there are 3 possible results from simulations and only 2 from calculations or using the streak calculator.
This is why I do not show my studies yet, since all situations are not yet complete.
That brings me back to the Craps question that was asked earlier. I found an error in my simulation code, that has been fixed and will address the earlier post below.
Quote: DeMangoI've got a craps question. If one places the 6 & 8, the odds are .375 on no hits before the 7 right? What are the odds of that happening 10 times in a row. Would that be .375^10? How about 10 in a row occurances in 480 rolls? It seems the result of 1.6% seems a little high according to nope27's friends calculator.
Now since I have completed my studies and simulations on Craps streaks I can now accurately answer your above question.
DeMango you are correct that the 1.6% seems high for 480 rolls.
The 1.6% probability of having at least 1 loss streak of 10 or more in a row in 480 rolls is also correct.
6&8 always working.
But those 480 rolls are only rolls of 6,7 and 8s. Meaning that there must be at least 960 (just an estimate) actual dice rolls to see that sequence.
The reason is we are only counting 6,7 and 8s in our initial calculation and so does the streak calculator.
I need to expand a few simulations to cover these and maybe add information to the streak calculator so one will understand that there is a difference between streaks for craps bets that resolve in 1 roll verses craps bets that resolve in 1 or more rolls.
If this does not make sense now it will in a future post.
Again, DeMango you are correct that the 1.6% chance of a losing streak of 10 in 480 rolls is too high.
When I am wrong, I do admit the fact.
How many total rolls does it take to see 480 6,7 and 8s?
1/(16/36) = 2.25*480 = 1080 rolls
So the 1.6% is for 1080 total dice rolls.
Now how about those 480 total dice rolls?
We expect to see 213.3 6,7 and 8s.
So enter 214,10 and .375 into the calculator and the answer is 0.7044245589027% or.007044245589027 and my simulations showed 68 out of 10,000.
Please accept my apology for giving you a wrong answer at first, but understanding the math and simulations of runs is my goal now and your question was a nice exercise in applying my understanding. I just answered it too early before I understood all my simulation data.
Quote: nope27
Also your simulations above you must be careful in evaluating craps bets that resolve on 1 roll and those that resolve on 1 or more rolls.
With place bets there are 3 possible results from simulations and only 2 from calculations or using the streak calculator.
This is why I do not show my studies yet, since all situations are not yet complete.
That brings me back to the Craps question that was asked earlier. I found an error in my simulation code, that has been fixed and will address the earlier post below.
I was scratching my head last night watching the Lakers in Portland and running simulations in WinCraps and testing them against the streak calculator.
The Lakers won in overtime and I finally won before midnight.
When I ran a sim on across place bets vs 7, the only way I could reconcile the sim results and the calculator results was not to count the horn numbers that rolled. Then I came to the same conclusion you did about bets resolving with 1 or more rolls.
Also, the percentages can be misleading by themselves. The average, standard deviation and mode together tell a better story,IMO, and I wonder if you also have gathered that data.
Example is in 54 total dice rolls, about half hour of play, I come up with these probabilities:
a run of 4 or more, at least 1 time 0.9999
a run of 4 or more, at least 2 times 0.9925
a run of 4 or more, at least 3 times 0.907
a run of 4 or more, at least 4 times 0.599
mean: 3.76
sd: 1.01
mode: 4
The distribution:
0 1 0.0001
1 74 0.0074
2 855 0.0855
3 3080 0.308
4 3775 0.3775
5 1799 0.1799
6 388 0.0388
7 28 0.0028
8 0 0
It appears to me that the relative frequencies give a better picture instead of the cumulative frequencies.
Just my thoughts. I know it has nothing to do with finding your elusive formula but I am looking ahead to see how one would apply this at an actual craps table.
Quote: guido111
The probability of getting at least 1 run of 4 losses or more in a row in 10 trials is 27.7326854715615% using the streak calculator.
How about getting a run of exactly 4 losses in a row in 10 trials?
It is a different question and should have a different answer.
If you want to know the answer to this question simply calculate the probability of losing 5 or more in a row and subtract that from the first calculation.
For "pass line craps"
23.4229% probability of getting a winning streak of at least 4 out of 10
10.2886% probability of getting a winning streak of at least 5 out of 10
13.1343% probability of getting a winning streak of exactly 4 out of 10
Quote: pacomartinIf you want to know the answer to this question simply calculate the probability of losing 5 or more in a row and subtract that from the first calculation.
For "pass line craps"
23.4229% probability of getting a winning streak of at least 4 out of 10
10.2886% probability of getting a winning streak of at least 5 out of 10
13.1343% probability of getting a winning streak of exactly 4 out of 10
Thanks for the refresher.
I know that works for independent events so I did a few sims to see how much of an error one can have since runs are not an independent event.
They are very close.
In 500 million session sims for p<= .5 the numbers are quite close.
I noticed when p= .6 the error is ~1%.
p= .7 the error is ~2.38%.
I say close is good enough to know where one stands.
So far for me...
The math of streaks and of multiple k-streaks in n-trials is turning out to be quite fascinating and challenging.
I am just wondering if it has any practical use in a casino.
There are two interpretations of the percentages
(1) Streak of wins or losses: For instance the probability of getting a streak of 3 out of 3 games is 25%
(2) Run of losses: The probability of two losses out of two games is 25%
Likewise the percentage of getting a streak of 3 out of 10 plays is the same as getting 2 losses out of 9 plays assuming no house edge:.
-----------------------------
The blanks in the upper right hand corner are illogical situations. You can't have a run of 8 unless you have played 8 or more times.
-----------------------------
You can think of this table as a limit. If you add different house edges the probability of reaching this situation is lower.
-----------------------------
The lead number in each column is 1/2 to different powers.
-----------------------------
The 6 losses in a row is in red, because the standard settings for ratio of max/min in most table games in a casino is 100 which permits you to double your bet 6 times in a row if you are stupidly playing Martingale.
It is a common mistake to believe that finding a table that permits more doubling than 6 will improve the odds at Martingale. The mathematics works out nearly identical regardless of how many times you can double. Even with no house edge you are twice as likely to burn out with Martingale as you are to double the minimum bankroll required. The house edge makes it worse.
-----------------------------
I showed the beginning of the table then moved to 80 some plays. At this point the more degenerate conditions of very low numbers of streaks are very close to 100% (given the number of decimal places ). This is when the special case approaches 50%. So for a coin toss you would expect to get to this many plays before you have an even chance of a 6 loss in a row. Given the house edge of the actual game, it will be a fewer number of plays.
| streak | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|
| loss | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 3 | 2 | 25.0000% | |||||||
| 4 | 3 | 37.5000% | 12.5000% | ||||||
| 5 | 4 | 50.0000% | 18.7500% | 6.2500% | |||||
| 6 | 5 | 59.3750% | 25.0000% | 9.3750% | 3.1250% | ||||
| 7 | 6 | 67.1875% | 31.2500% | 12.5000% | 4.6875% | 1.5625% | |||
| 8 | 7 | 73.4375% | 36.7188% | 15.6250% | 6.2500% | 2.3438% | 0.7813% | ||
| 9 | 8 | 78.5156% | 41.7969% | 18.7500% | 7.8125% | 3.1250% | 1.1719% | 0.3906% | |
| 10 | 9 | 82.6172% | 46.4844% | 21.6797% | 9.3750% | 3.9063% | 1.5625% | 0.5859% | 0.1953% |
| 11 | 10 | 85.9375% | 50.7813% | 24.5117% | 10.9375% | 4.6875% | 1.9531% | 0.7813% | 0.2930% |
| 12 | 11 | 88.6230% | 54.7363% | 27.2461% | 12.4512% | 5.4688% | 2.3438% | 0.9766% | 0.3906% |
| 13 | 12 | 90.7959% | 58.3740% | 29.8828% | 13.9404% | 6.2500% | 2.7344% | 1.1719% | 0.4883% |
| 14 | 13 | 92.5537% | 61.7188% | 32.4219% | 15.4053% | 7.0190% | 3.1250% | 1.3672% | 0.5859% |
| 15 | 14 | 93.9758% | 64.7949% | 34.8694% | 16.8457% | 7.7820% | 3.5156% | 1.5625% | 0.6836% |
| 16 | 15 | 95.1263% | 67.6239% | 37.2284% | 18.2617% | 8.5388% | 3.9032% | 1.7578% | 0.7813% |
| 17 | 16 | 96.0571% | 70.2255% | 39.5020% | 19.6533% | 9.2896% | 4.2892% | 1.9531% | 0.8789% |
| 18 | 17 | 96.8102% | 72.6181% | 41.6931% | 21.0213% | 10.0342% | 4.6738% | 2.1477% | 0.9766% |
| 19 | 18 | 97.4194% | 74.8184% | 43.8049% | 22.3660% | 10.7727% | 5.0568% | 2.3418% | 1.0742% |
| 20 | 19 | 97.9122% | 76.8419% | 45.8403% | 23.6877% | 11.5051% | 5.4382% | 2.5356% | 1.1717% |
| 21 | 20 | 98.3109% | 78.7028% | 47.8019% | 24.9870% | 12.2315% | 5.8182% | 2.7290% | 1.2691% |
| 87 | 86 | 100% | 100% | 95.4267% | 75.8502% | 49.0574% | 27.7948% | 14.6808% | 7.4879% |
| 88 | 87 | 100% | 100% | 95.5924% | 76.2614% | 49.4755% | 28.0850% | 14.8501% | 7.5791% |
| 89 | 88 | 100% | 100% | 95.7520% | 76.6655% | 49.8903% | 28.3739% | 15.0191% | 7.6702% |
| 90 | 89 | 100% | 100% | 95.9059% | 77.0628% | 50.3016% | 28.6617% | 15.1877% | 7.7611% |
| 91 | 90 | 100% | 100% | 96.0542% | 77.4533% | 50.7095% | 28.9483% | 15.3560% | 7.8520% |
