February 18th, 2025 at 8:45:50 AM
permalink
The object of this thread is to discuss a fair way to divide a cake. Assume you have no measurement tools. Also assume the cake is not uniform. In this example, assume there is one strawberry and some blueberries.
There are two possible goals:
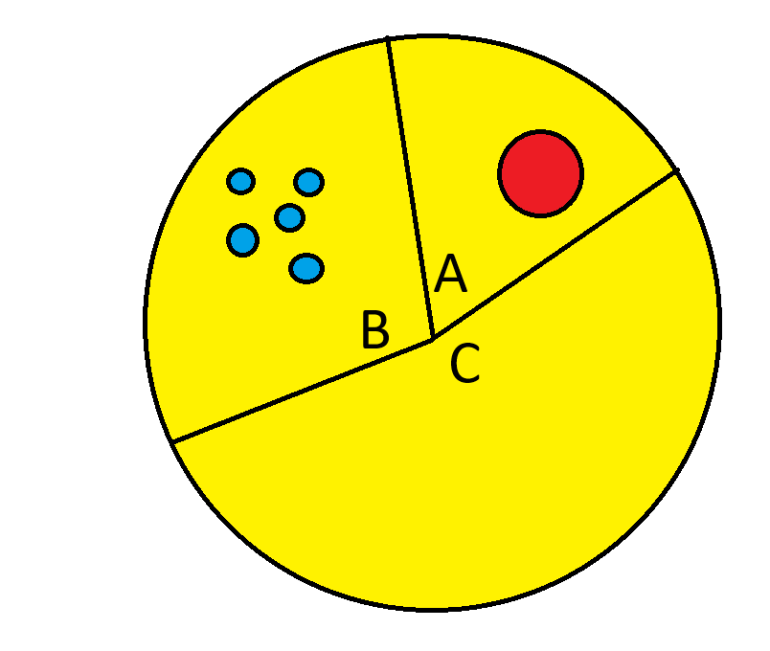
Let's keep it simple to start and assume just three people.
I'll start with how I would do it under the second goal listed above. It is not necessarily compliant with the first.
Example:
Player 1 cuts pieces A, B and C as shown above.
Players 2 and 3 both want piece B. Player 3 favors piece C as his second choice.
Player 2 cuts off section D from piece B and adds it to piece C.
Player 3 chooses C+D, which he gets.
Player 2 gets piece B.
Player 1 gets piece A.
There are two possible goals:
- The goal is to have nobody with "cake envy," meaning nobody feels somebody else got a better piece.
- Everybody at least feels he got equal or more than his fair share, although he may feel somebody else got more than he did.

Let's keep it simple to start and assume just three people.
I'll start with how I would do it under the second goal listed above. It is not necessarily compliant with the first.
- Choose somebody to cut the cake into three pieces he deems fair. If nobody volunteers, choose randomly. Call the cutter player 1.
- The other two indicate, which piece they want.
- If step 2 results in different choices, those two people get the piece they chose and the cutter gets the last piece.
- If step 2 results in the same choice, then determine a second cutter, randomly if necessary. Call the second cutter player 2 and the remaining person player 3.
- Player 2 asks player 3 his second favorite piece.
- Player 2 cuts off a portion of the piece they both desire to the second favorite piece of player 3 that he deems fair.
- Player 3 makes a choice after the cut of player 2.
- Player 2 gets the piece(s) after player 3's choice.
- Player 1 gets the remaining piece.
Example:
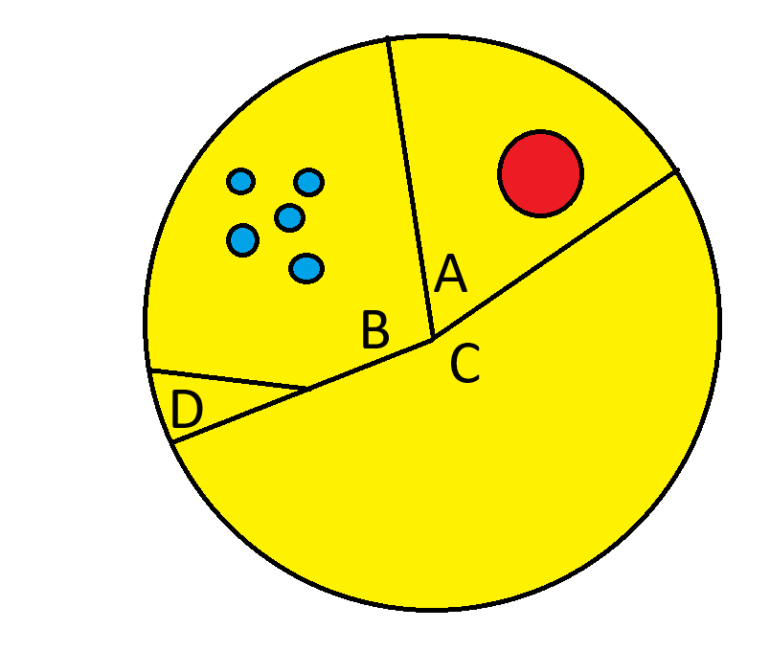
Player 1 cuts pieces A, B and C as shown above.
Players 2 and 3 both want piece B. Player 3 favors piece C as his second choice.
Player 2 cuts off section D from piece B and adds it to piece C.
Player 3 chooses C+D, which he gets.
Player 2 gets piece B.
Player 1 gets piece A.

Last edited by: Wizard on Feb 18, 2025
"My life is spent in one long effort to escape from the commonplace of existence. These little problems help me to do so." -- Sherlock Holmes
February 18th, 2025 at 10:24:09 AM
permalink
I just tell everyone the cake was not for them and eat it myself.....
All animals are equal, but some are more equal than others
February 18th, 2025 at 10:36:34 AM
permalink
My first rule would be the person who makes the cuts chooses last.
It appears the Premium pieces take up a third of the pie. I'd cut out the two premium pieces.
I'd divide the remaining two-thirds into six slices and give everyone two slices.
At this point, each of the three has had more cake than they need and can't be envious of their fellow cake eaters.
Hopefully, they learn that envy sucks, and there is a price to be paid for it. Next time, they can work together, and everyone gets an equal share they can eat rather than sharing nothing.
It appears the Premium pieces take up a third of the pie. I'd cut out the two premium pieces.
I'd divide the remaining two-thirds into six slices and give everyone two slices.
At this point, each of the three has had more cake than they need and can't be envious of their fellow cake eaters.
Hopefully, they learn that envy sucks, and there is a price to be paid for it. Next time, they can work together, and everyone gets an equal share they can eat rather than sharing nothing.
The older I get, the better I recall things that never happened
February 18th, 2025 at 12:46:41 PM
permalink
Are we assuming a circular cross section (cylindrical, hemispherical, or similar) cake (pizza)?
May the cards fall in your favor.
February 18th, 2025 at 12:48:42 PM
permalink
I suppose saying, Take whatever you like, and genuinely not caring what was left, would still open the possibility of unfairness between the other two.
I tell you itís wonderful to be here, man. I donít give a damn who wins or loses. Itís just wonderful to be here with you people.
https://wizardofvegas.com/forum/gambling/betting-systems/33908-the-adventures-of-mdawg/
February 18th, 2025 at 1:27:58 PM
permalink
For two people, it's "you cut, I choose."
February 18th, 2025 at 2:17:20 PM
permalink
This is a fairly well-known problem, and I have heard a few "solutions" over the years.
Person 1 cuts a slice
Person 2 then either takes that slice, or cuts a slice next to it to make a bigger slice.
Keep going until someone takes the most recently cut "combined slice."
I saw a comic strip that mentioned this; the person who cut the cake licked both sides of the knife first.
Person 1 cuts a slice
Person 2 then either takes that slice, or cuts a slice next to it to make a bigger slice.
Keep going until someone takes the most recently cut "combined slice."
Quote: smoothgrhFor two people, it's "you cut, I choose."
link to original post
I saw a comic strip that mentioned this; the person who cut the cake licked both sides of the knife first.
February 18th, 2025 at 3:56:19 PM
permalink
It is not possible to cut the cake into fair slices, So fairness can only be gained
by a fair contest from which selection order is determined, The fairness of the selection process
insures agreeableness in the participants.
Roshambo.
by a fair contest from which selection order is determined, The fairness of the selection process
insures agreeableness in the participants.
Roshambo.
February 18th, 2025 at 4:26:21 PM
permalink
Quote: DieterAre we assuming a circular cross section (cylindrical, hemispherical, or similar) cake (pizza)?
link to original post
It doesn't matter. For purposes of discussion, an unusual size works best.
"My life is spent in one long effort to escape from the commonplace of existence. These little problems help me to do so." -- Sherlock Holmes
February 18th, 2025 at 4:36:22 PM
permalink
Quote: ThatDonGuyThis is a fairly well-known problem, and I have heard a few "solutions" over the years.
Person 1 cuts a slice
Person 2 then either takes that slice, or cuts a slice next to it to make a bigger slice.
Keep going until someone takes the most recently cut "combined slice."
I don't think we need to put things in spoiler tags as there is no exact solution.
To your idea, let's assume there are three people and it's a uniform cake. Person 1 cuts off 30%. Person 2 votes no and adds 20% more. Person 3 happily accepts 50% of the cake. Person 1 would definitely have cake envy.
"My life is spent in one long effort to escape from the commonplace of existence. These little problems help me to do so." -- Sherlock Holmes
February 18th, 2025 at 5:10:23 PM
permalink
The guest of honor-birthday, anniversary, retirement, bridal shower, etc, gets to choose what type of piece they want-strawberry, blueberry or plain. Assuming they want the strawberry, and the other 2 want blueberries, then split the blueberries down the middle. If somebody wants a plain piece, that lessens chance for piece envy. Give everyone an equal size share, even if split into two different pieces.
If the guest of honor doesn't want the strawberry and wants blueberries, then split the blueberries down the middle and someone else can take either the BB piece or the SB piece.
If the guest of honor wants a plain piece then one person gets the SB if they want and another gets the BB piece if they want. If the SB is big enough perhaps split that down the middle to share.
At the end, Geno gets the leftovers !
If the guest of honor doesn't want the strawberry and wants blueberries, then split the blueberries down the middle and someone else can take either the BB piece or the SB piece.
If the guest of honor wants a plain piece then one person gets the SB if they want and another gets the BB piece if they want. If the SB is big enough perhaps split that down the middle to share.
At the end, Geno gets the leftovers !
February 18th, 2025 at 5:19:37 PM
permalink
Quote: rainmanIt is not possible to cut the cake into fair slices, So fairness can only be gained
by a fair contest from which selection order is determined, The fairness of the selection process
insures agreeableness in the participants.
Roshambo.
link to original post
Why? If you isolate the two premium pieces, you slice each in three and distribute it equally along with one third of the non premium. Each of the three gets exactly the same.
The older I get, the better I recall things that never happened
February 18th, 2025 at 7:59:50 PM
permalink
i think this is one of those things where no matter what solution we decide on, there is always an example where it fails to be the most fairly divided.
here are a couple I've come up with that I like and work just fine with any number of participants.
for the economists:
-cut the cake into a number of pieces.
-auction off each piece after giving each participant an equal amount of pretend dollars to use.
-could use real dollars in the auction with the money be divided equally among the people who didn't win. That brings up the philosophical issue of fairness when each participant starts with a different amount of dollars.
For the game theorists:
-instead of "I cut, you choose", it could be "you get a bit, I get a bite".
-each participant submits a bid for what they want the size of a bite to be.
-whomever submitted the smallest size of a bite takes a bite of that size.
-whomever submitted the second smallest size of a bite takes a bite of that size.
-keep going like that until everyone has taken a bite, then go back for seconds and keep going until the whole cake is gone.
-it's possible someone doesn't get a bite. Should have bid for a smaller bite.
-it's also possible two people say a bite is 1 atom of cake, while the third person says a bite is the whole cake. Should have bid bigger.
here are a couple I've come up with that I like and work just fine with any number of participants.
for the economists:
-cut the cake into a number of pieces.
-auction off each piece after giving each participant an equal amount of pretend dollars to use.
-could use real dollars in the auction with the money be divided equally among the people who didn't win. That brings up the philosophical issue of fairness when each participant starts with a different amount of dollars.
For the game theorists:
-instead of "I cut, you choose", it could be "you get a bit, I get a bite".
-each participant submits a bid for what they want the size of a bite to be.
-whomever submitted the smallest size of a bite takes a bite of that size.
-whomever submitted the second smallest size of a bite takes a bite of that size.
-keep going like that until everyone has taken a bite, then go back for seconds and keep going until the whole cake is gone.
-it's possible someone doesn't get a bite. Should have bid for a smaller bite.
-it's also possible two people say a bite is 1 atom of cake, while the third person says a bite is the whole cake. Should have bid bigger.
February 18th, 2025 at 8:16:57 PM
permalink
Ah, non-fungible types of slices. Someone might detest either blueberries, or strawberries, or both.
Being this is a social event my first priority is to ensure no one gets a slice they are unwilling to eat. So I am going to give them slips of paper and have them tell me which slice they like the least. If there is one slice with one non-veto, that person gets that slice, and then we repeat the process with two, with the understanding that they will have to draw lots if they do not veto different slices.
Works the same way with an unlimited number of people/slices. For n people we start with 1 slice being vetoed first, and we can increase the number of vetoes per round until we find slices that only one person is willing to eat. Or perhaps we can allow each eater an unlimited number of vetoes per round, but the person using the fewest number of vetoes wins the tiebreaker in case a slice is accepted by more than one person.
Being this is a social event my first priority is to ensure no one gets a slice they are unwilling to eat. So I am going to give them slips of paper and have them tell me which slice they like the least. If there is one slice with one non-veto, that person gets that slice, and then we repeat the process with two, with the understanding that they will have to draw lots if they do not veto different slices.
Works the same way with an unlimited number of people/slices. For n people we start with 1 slice being vetoed first, and we can increase the number of vetoes per round until we find slices that only one person is willing to eat. Or perhaps we can allow each eater an unlimited number of vetoes per round, but the person using the fewest number of vetoes wins the tiebreaker in case a slice is accepted by more than one person.
February 18th, 2025 at 9:43:26 PM
permalink
Quote: WizardQuote: DieterAre we assuming a circular cross section (cylindrical, hemispherical, or similar) cake (pizza)?
link to original post
It doesn't matter. For purposes of discussion, an unusual size works best.
link to original post
I thought I had an elegant general solution for round pies, but it falls apart with 3 prisoners.
May the cards fall in your favor.
February 19th, 2025 at 6:16:05 AM
permalink
This method will work with any number of people.
- Someone cuts a piece he would accept as fair for himself.
- Everyone else is given a chance to object, indicating he would also accept that piece. If there are no objectors, the cutter gets that piece. Otherwise, go to step 3.
- One of the objectors must cut off a little piece from the piece in step 1 that he would still accept for himself.
- Again, there is a chance for objections. If there are none, the cutter from step 3 gets that piece. Otherwise an objector must cut off a little bit.
- This process continues until there are no objections.
- The rest of the group repeats this process to determine the next piece.
"My life is spent in one long effort to escape from the commonplace of existence. These little problems help me to do so." -- Sherlock Holmes
February 19th, 2025 at 6:35:16 AM
permalink
This is why the Gordian knot puzzled so many mathletes. They refuse to consider the most straightforward solution and tried to be clever.
The older I get, the better I recall things that never happened
February 19th, 2025 at 7:09:10 AM
permalink
everyone assigns values to all parts of the cake. A third-party arbiter who's only purpose is to maximize value splits the cake.
example, one person only likes the strawberry and dislikes everything else; one person only likes the blueberries and dislikes everything else; one person dislikes the fruit and only likes the plain part. Everyone can get 100% of the value of the cake, so why not just do that?
If a fourth person only likes the edge portion, they can get a ring of an infinitesimal thickness giving them a piece that covers the entire circumference. They would also get 100% of the value, while one person would only lose an infinitesimal amount.
Thinking that giving all three people 1/3 of the value of the cake is "fair" will often mean losing value. That makes for a lot of times it is not fair.
example, one person only likes the strawberry and dislikes everything else; one person only likes the blueberries and dislikes everything else; one person dislikes the fruit and only likes the plain part. Everyone can get 100% of the value of the cake, so why not just do that?
If a fourth person only likes the edge portion, they can get a ring of an infinitesimal thickness giving them a piece that covers the entire circumference. They would also get 100% of the value, while one person would only lose an infinitesimal amount.
Thinking that giving all three people 1/3 of the value of the cake is "fair" will often mean losing value. That makes for a lot of times it is not fair.


