Calculating Count Frequency

Hello everyone,

Imagine a simple game where you are dealt one card.
If it’s an Ace you get 11:1, if not you lose your bet.
Say the game is dealt out of a six deck shoe, so one could assign a count and keep track of the number of Aces that are left in the shoe.
Through a simple analysis it comes out that at TC 1 the edge is 0%, TC 2 it’s 9.09%, TC 3 it’s 20% etc.
But is it possible to calculate the frequency of each count, i.e. how often the shoe will reach TC1,TC2,TC3 etc..? I mean instead of doing a simulation.

Thanks

These can be calculated exactly. For a question like this, I often refer it to the guru ThatDonGuy. Just like blackjack card counting, you may assign each card a tag number of +1, 0, or -1 to calculate the resulting true count frequencies. In your example, what tag numbers do you assign to each card?

Quote: gunbj

Hello everyone,

Imagine a simple game where you are dealt one card.
If it’s an Ace you get 11:1, if not you lose your bet.
Say the game is dealt out of a six deck shoe, so one could assign a count and keep track of the number of Aces that are left in the shoe.
Through a simple analysis it comes out that at TC 1 the edge is 0%, TC 2 it’s 9.09%, TC 3 it’s 20% etc.
But is it possible to calculate the frequency of each count, i.e. how often the shoe will reach TC1,TC2,TC3 etc..? I mean instead of doing a simulation.

Thanks
link to original post

I suspect that this game is not that much about counting the aces but rather about counting the cards already dealt, which have not been aces.

With odds 11:1 the player will break even if togehter with each ace only 11 non-ace cards are dealt. If fewer than 11 non-ace cards are dealt for any ace the player will make money.

A six deck shoe has 24 aces. So if all 24 aces are dealt before 24 * 11 = 264 other cards are dealt the palyer will make money on that shoe.

If the shoe is dealt down to the last card, the strategy would be to bet minimum on the first 24 non-ace cards and bet minimum on 11 more non-ace cards for each ace already dealt. After that, the player should bet big on each following card, because the player now is guaranteed to not lose any more - the worst case is to break even for the remaining shoe.

If a cut card is used to lower shoe penetration, the number of possible aces has to be determined and the strategy adapted accordingly.
number of aces n = integer(24 * portion of shoe played)
Bet minimum on the first n non-ace cards and bet minimum on 11 more non-ace cards for each ace already dealt. After that, bet big up to the nth ace or up to the cut card, whichever happens first.
In this case the player will be down on individual shoes, but in the long run will be up because n is the long run average number of aces to be expected for that short shoe.

Quote: aceside

These can be calculated exactly. For a question like this, I often refer it to the guru ThatDonGuy. Just like blackjack card counting, you may assign each card a tag number of +1, 0, or -1 to calculate the resulting true count frequencies. In your example, what tag numbers do you assign to each card?
link to original post

I think for a game like this, since the Aces are the only important cards, it would make sense to assign +1 to any card that is not an Ace, and -12 to Aces. Then to find the True Count one would divide the running count by 12 and then again by the number of decks remaining.
For example say the RC is +53, divide by 12 and round down it’s 4, divide by number of decks left (say 3) = TC +1
Unless there’s a better way.

You may reference the Ten Side Count for Blackjack insurance, in which a perfect side count for Insurance purposes would count Tens as -9 and all other cards as +4.

Actually, it’s not so perfect. Let me quote Eliot’s post about insurance. “For example, in a single deck game, there are 16 face cards and 35 non-face cards (the Ace is already exposed). It follows that the true odds for Insurance are 35-to-16, while it pays 32-to-16. The edge on the Insurance bet is then 3/51, or 5.8824%.”

Quote: aceside

These can be calculated exactly. For a question like this, I often refer it to the guru ThatDonGuy. Just like blackjack card counting, you may assign each card a tag number of +1, 0, or -1 to calculate the resulting true count frequencies. In your example, what tag numbers do you assign to each card?
link to original post

A callout, and on my birthday to boot (#62 - and I got a present from the federal government; a 10% increase to my pension when I retire)

Quote: gunbj

Hello everyone,

Imagine a simple game where you are dealt one card.
If it’s an Ace you get 11:1, if not you lose your bet.
Say the game is dealt out of a six deck shoe, so one could assign a count and keep track of the number of Aces that are left in the shoe.
Through a simple analysis it comes out that at TC 1 the edge is 0%, TC 2 it’s 9.09%, TC 3 it’s 20% etc.
But is it possible to calculate the frequency of each count, i.e. how often the shoe will reach TC1,TC2,TC3 etc..? I mean instead of doing a simulation.

Thanks
link to original post

Note that this is an unbalanced count, with Ace = 1 and everything else = 0.

Question: what, exactly, are you trying to figure out?
What is the probability that a shoe will reach TC 1, TC 2, and so on?
Or, how often in a shoe should it reach TC 1, TC 2, and so on?
Or is it something else?

You don't specify what count you are using. This is a straightforward probability problem.

The probability that there are 24 aces in the shoe before any cards are dealt is 100%. The probability that there are 24 aces left after 1 card is dealt is 12/13 (that is, 288/312). The probability that there are 23 aces left after 1 card is dealt is 1/13.

For the former case, the probability that there are 24 aces left after a second card is dealt is (12/13)*(287/311)

For the former case, the probability that there are 23 aces left after a second card is dealt is (12/13)*(24/311)

For the latter case, the probability that there are 24 aces left after a second card is dealt is zero.

For the latter case, the probability that there are 23 aces left after a second card is dealt is (1/13)*(287/311)

For the latter case, the probability that there are 22 aces left after a second card is dealt is (1/13)*(23/311)

Just keep repeating until you know the probability distribution for aces in the deck at each stage.

Doing the calculation for a 312-card shoe is tedious. Simulation is so quick and easy, I would just do that.

The Hypergeometric Distribution will tell you the CDF for remaining aces after you draw any number of cards.
https://en.wikipedia.org/wiki/Hypergeometric_distribution#Multivariate_hypergeometric_distribution

You can determine how often you will get a shoe that reaches TC1 at some point, but you might be more interested in how often it will get to TC1 by a particular point in the shoe.
By TC1, I am assuming that 1 out of every 12 remaining cards is an Ace. This is an unbalanced count starting at 24 with Ace = -1 and everything else = 0, and the "actual" TC is 13/12, as there would be 13/12 Aces left in 52 cards.
There is no "easy" way to do this that I know of other than brute force counting.

I get that you should reach an advantage play count at some point in the first third of the shoe about half the time.

Quote: ThatDonGuy

You can determine how often you will get a shoe that reaches TC1 at some point, but you might be more interested in how often it will get to TC1 by a particular point in the shoe.
By TC1, I am assuming that 1 out of every 12 remaining cards is an Ace. This is an unbalanced count starting at 24 with Ace = -1 and everything else = 0, and the "actual" TC is 13/12, as there would be 13/12 Aces left in 52 cards.
There is no "easy" way to do this that I know of other than brute force counting.

I get that you should reach an advantage play count at some point in the first third of the shoe about half the time.
link to original post

Makes sense, thank you very much

Quote: gunbj

Hello everyone,

Imagine a simple game where you are dealt one card.
If it’s an Ace you get 11:1, if not you lose your bet.
Say the game is dealt out of a six deck shoe, so one could assign a count and keep track of the number of Aces that are left in the shoe.
Through a simple analysis it comes out that at TC 1 the edge is 0%, TC 2 it’s 9.09%, TC 3 it’s 20% etc.
But is it possible to calculate the frequency of each count, i.e. how often the shoe will reach TC1,TC2,TC3 etc..? I mean instead of doing a simulation.

Thanks
link to original post

I wish I had thought this through more carefully before I made my first replies. Some commenters say that you need to do brute force calculations to get the exact answer. This would be time consuming for 6-decks and even worse for 8 decks.

I mentioned the Hypergeometric Distribution and gave a link to wiki. However, I am not sure that link is very useful to the uninitiated. Here is another link that includes a calculator:
https://mathworld.wolfram.com/HypergeometricDistribution.html
If Wizard has a link that covers this, I cannot find it so I am linking to an external page that I tried and seems safe.

I used the calculator to get the probability that zero aces would be dealt from a six-deck shoe after one full deck was dealt.

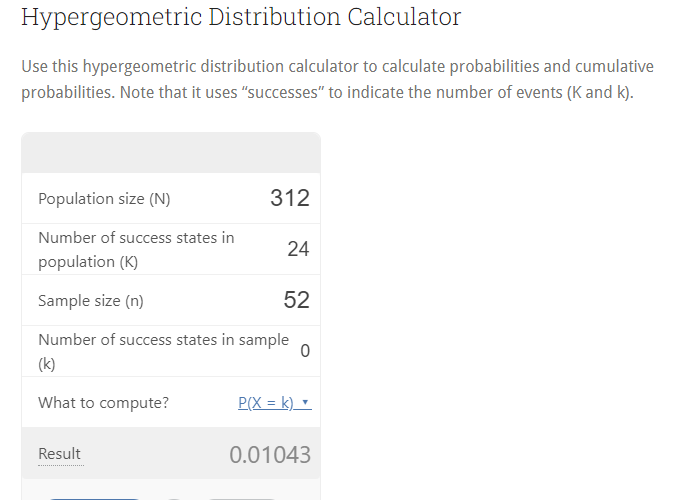
The population is 6*52 = 312 cards.
The number of success states (Aces) is 24.
Sample size means I looked at 52 cards.
Number of success states in sample is set to zero, so all 24 aces are left in the shoe.
'What to compute' is set to =, meaning I want the probability that exactly zero aces were dealt in the first 52 cards.

I easily verified this answer, 0.01043, using a spreadsheet.

If you wanted to ask how often there were 8 or fewer aces dealt from the shoe after half the cards were seen, the calculator will give you that answer (0.06779).

I don't think that there is a Hypergeometric Distribution built into and common spreadsheets. However, if you really need to create a table of results, you should be able to program the formula yourself using other preprogrammed functions. Please let us know if you succeed.