Thread Rating:
This is known as The Haberdasher's Puzzle/Problem
Here is the original footage:
part 1
part 2
part 3
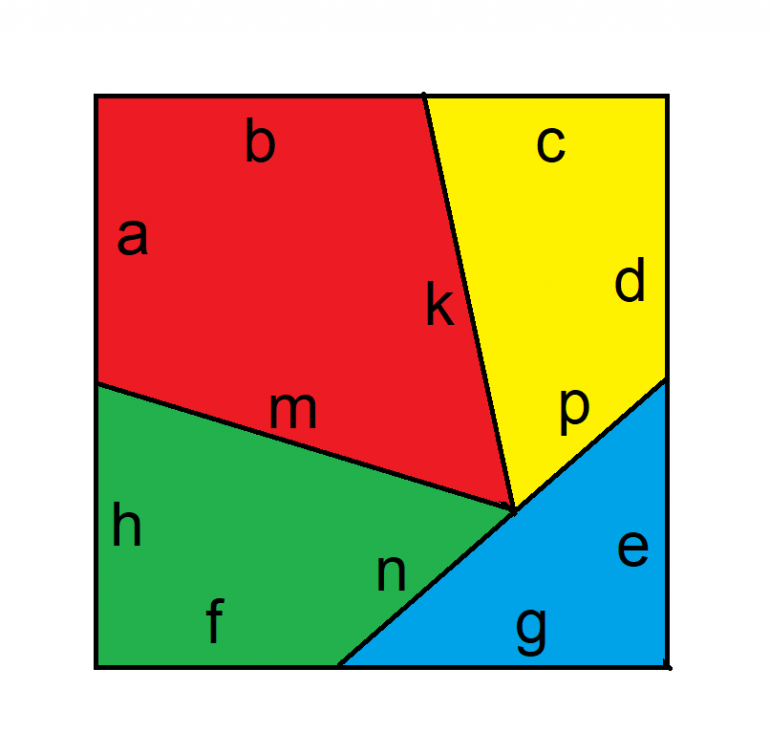
Here is a picture of the pieces forming a square:

Here is the triangle.

My question for the thread is what are the dimensions of the four pieces? Please assume the square has sides of length 1.
I have already worked on this a fair bit and have an answer. It's possible there are an infinite number of answers.
The Area of the triangle = Area of square = 1^2 = 1
For equilateral triangle of side S, will have height sqrt(3)/2 * S and area = (1/2)*(S/2)*(sqrt(3)/2 * S)
So I get side of triangle S = 8/sqrt(3)
In my drawing,
a) the two crossing lines are perpendicular. Both are length = 1 (side of of square) and A1=A2=A3=A4 = 1/2
b) the crossing lines are symmetric, so dotted red line makes an equilateral triangle of side B = sqrt(2)/2
c) So C = S-B = 8/sqrt(3) - sqrt(2)/2
d) E = B again by symmetry
e) D = .5*(S-E) = .5*(S-B) = .5*C = .5 *(8/sqrt(3) - sqrt(2)/2)
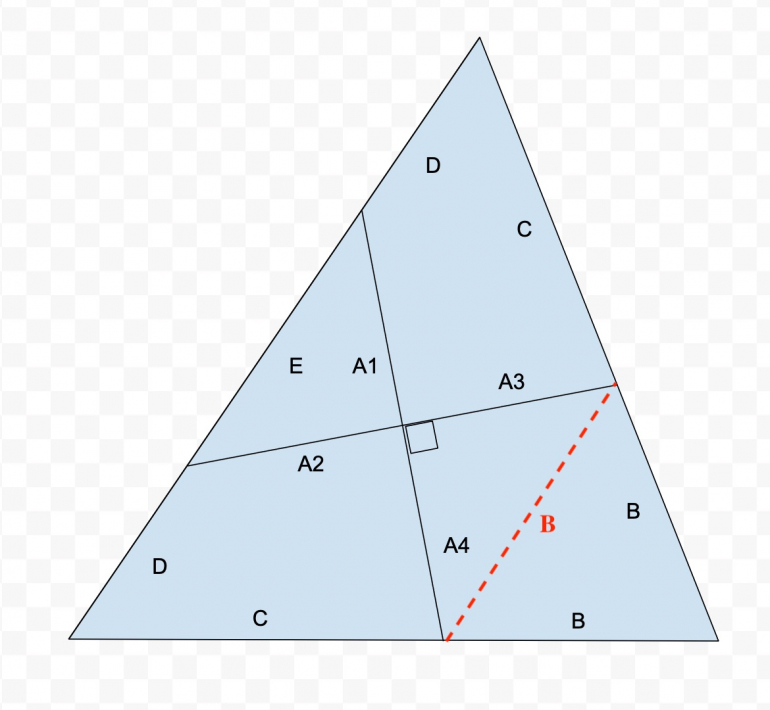
The needed conditions I think in general are that
i) A1+A2 =1 (side of triangle) and they are perpendicular
ii) A3+A4 =1 (side of triangle) and they are perpendicular
On original pic I labelled how they would be
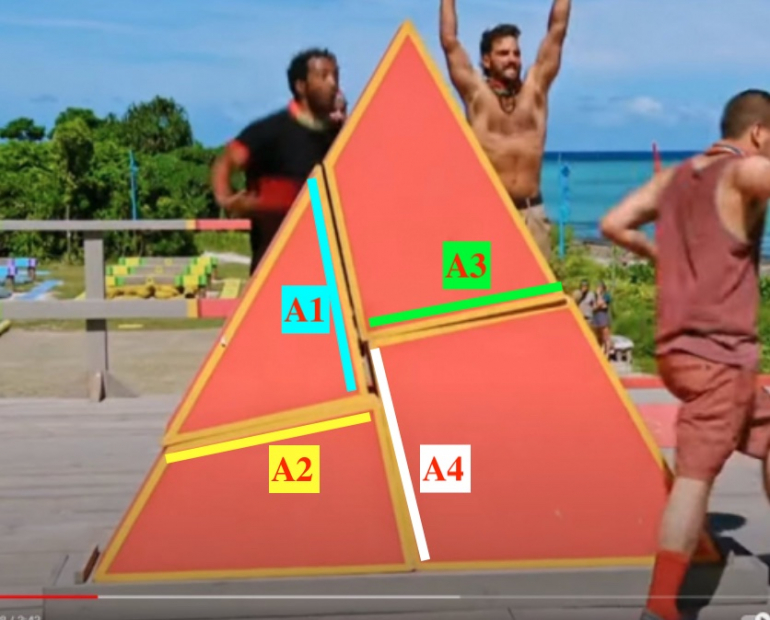
Anyway, that is a shot.....may have done my trig, Pythagorean theorem, or algebra wrong.....but art least you aren't talking to yourself?
I was only looking at the interior crosses and needing right angles and two legs adding to give side of square.
BUT.....I also need the pieces to fit together to form square. in my picture that would mean B=C....and sadly that does not work.
Will think about it more if I have the time
Quote: chevyCurrent opinion.......My above construction fails
link to original post
I'm glad to see interest in this problem.
I too did it your way at first and accused the triangle on Survivor of not being a true equilateral triangle. However, I later found an error in my work and deleted the accusation.
In your diagram you have D twice, indicating those positions are the same length. My solution does not have them equal. Close though.
For the actual dimensions of the pieces, I ask for only a handful of decimal places, like six. I think to put them in closed form would be too much to ask.
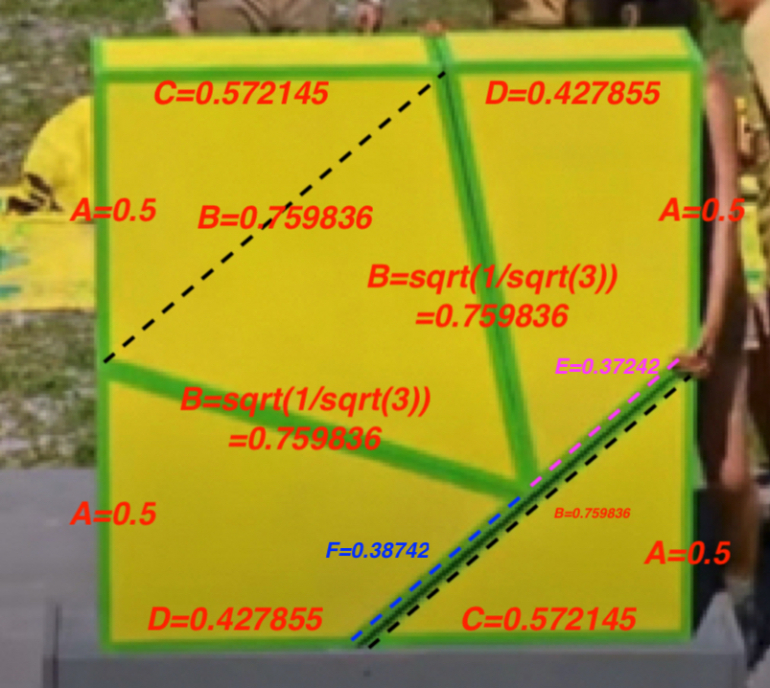
Here it is in picture form.
I got two values for E&F (per Wizard's comment.....) Close but different. I assigned the longer one to the segment that I thought had to be longer, but can't conclusively prove it....so they could be switched.
Quote: chevyMy second (and probably final attempt)
Here it is in picture form.
I got two values for E&F (per Wizard's comment.....) Close but different. I assigned the longer one to the segment that I thought had to be longer, but can't conclusively prove it....so they could be switched.
link to original post
I got the same value for B, my question to you is, on the kite piece, we know the two long sides are the same length, and that the adjacent angle is 60 degrees (since it's used as a corner on the triangle), wouldn't that mean it's an equilateral triangle? Which means that would make triangle ABC a 45, 45, 90 triangle? Or am I missing an extra step in there somewhere?
Quote: chevyMy second (and probably final attempt)
Here it is in picture form.
I got two values for E&F (per Wizard's comment.....) Close but different. I assigned the longer one to the segment that I thought had to be longer, but can't conclusively prove it....so they could be switched.
link to original post
I agree!
Quote: TheCapitalShipQuote: chevyMy second (and probably final attempt)
....clipped and moved to my reply....
link to original post
link to original post
TheCapitalShip: "I got the same value for B, my question to you is, on the kite piece, we know the two long sides are the same length, and that the adjacent angle is 60 degrees (since it's used as a corner on the triangle), wouldn't that mean it's an equilateral triangle? Which means that would make triangle ABC a 45, 45, 90 triangle? Or am I missing an extra step in there somewhere?"
"
Yes, I got that the "bottom of the kite" is a B-B-B equilateral triangle. (Third "B" is the dashed line)
Then to get C = sqrt (B^2 - A^2).....since ABC is right triangle and pythagorean theorem and we know B and A***
So the numbers don't end up as 45-45-90.
***You didn't mention it, but did you get A = 0.5? I used that fact in finding C. The top of left side is A and the bottom of the left side is A since they both come from the same cut on the triangle view. So each must be 0.5 (square side is 1)
Same for the right side by the way.
From this view, I used
ALB=A on Left Bottom of my square
ALT=A on Left Top of my square
ARB=A on Right Bottom of my square
ART=A on Right Top of my square
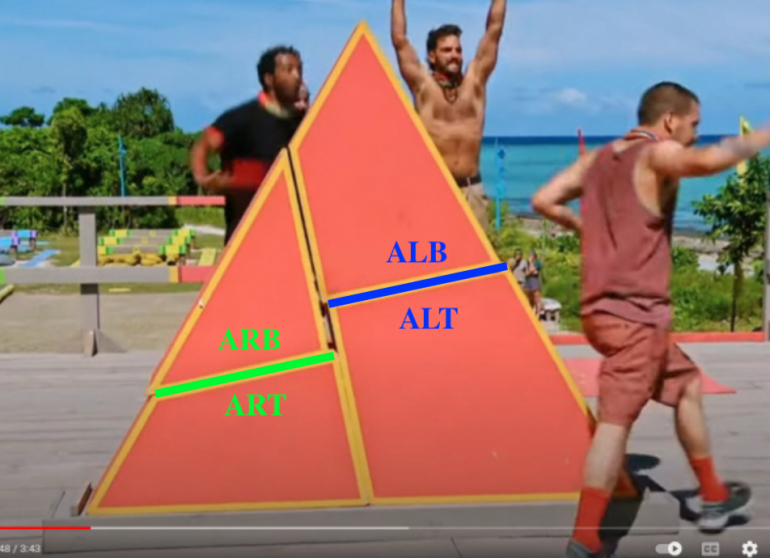
PS: As I see it, all the pieces in the survivor yellow team's square are the OPPOSITE side view of the survivor red team's triangle..i.e. we are seeing the construction from two different sides. (...easiest to see looking at the long side of the triangle piece.)
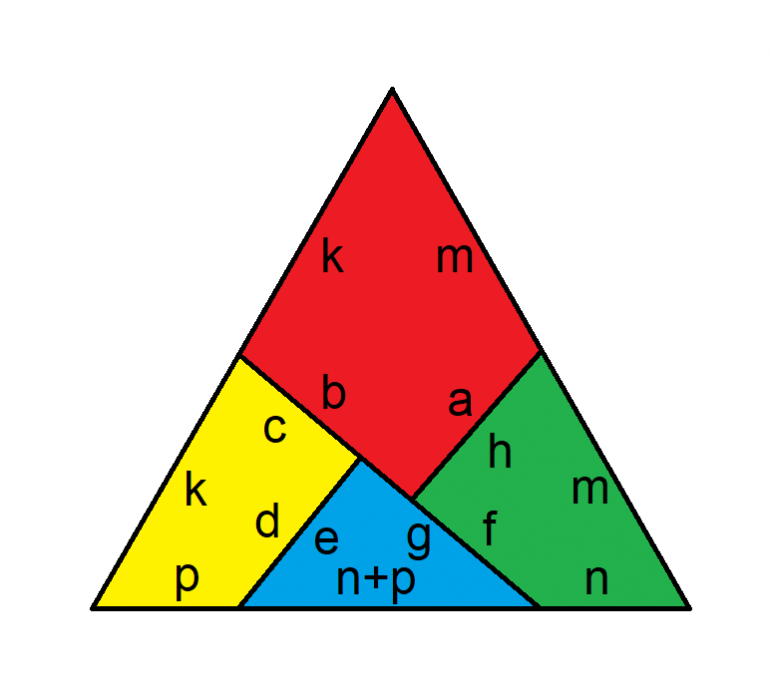
After computing the length of the sides of an equilateral triangle the first 10 equations were easy to come up with based on the lengths of the sides of the triangle and square, the common edges, and the blue right triangle. It took me awhile to come up with the equilateral triangle formed by K and M (K = M), giving an equation for A and B in terms of K. And then finally I used the triangle formed by the yellow and blue sections to come up with an equation for 2P + N in terms of C, G, and K.
A 0.500000000000000
B 0.572145321740578
C 0.427854678259422
D 0.500000000000000
E 0.500000000000000
F 0.427854678259422
G 0.572145321740578
H 0.500000000000000
K 0.759835685651595
M 0.759835685651595
N 0.386767938902278
P 0.373067746749317
red_area 0.393036330435146
blu_area 0.143036330435144
grn_area 0.234217477922977
yel_area 0.229709861206736
---------------------------
tot_area 1.000000000000000
Quote: WizardQuote: chevy
Here it is in picture form.
I got two values for E&F (per Wizard's comment.....) Close but different. I assigned the longer one to the segment that I thought had to be longer, but can't conclusively prove it....so they could be switched.
link to original post
I know previously said I agree with this, but I found two small disagreements.
You get E=0.37242. I get 0.386767939 =(3-SQRT(4*SQRT(3)-3))/(2*3^0.25)
You get F = 0.38742. I get 0.373067747 = (SQRT(4*SQRT(3)-3)-1)/(2*3^0.25)
Of course, I could be the one in error.
link to original post
I will gladly concede I am in error....
But I do note that my E is your F (within a reasonable margin of error for my numerical calc.) and vice versa. I did not solve for E and F analytically....I got down to solving for F and used a law of cosines on-line calculator (since you suggested numerical values would suffice.) so some rounding could come from that. Law of cosines solving for one of the adjacent sides is quadratic, and yielded the two answers for F (which do, by the wa. add up to the hypotenuse of the triangle piece....B=0.759836 on my pic (n+p in your nice drawing))
So my two QUADRATIC answers for F were F1, F2
F1 = 0.38742......and then I got E1 = B-F1 = 0.37242 which was just F2
F2 = 0.37242......and then I got E2 = B-F2 = 0.38742 which was just F1
In my "second attempt" I acknowledge that I got the two answers and simply assigned the pair to what looked correct on the survivor pic (the one being slightly longer), but that I had no proof. So I could have them switched and I accept that.
Then ,my question is, Did you (how did you) get unique answers for them.
Or
Quadratic suggests two possible answers, ... which by the way I would get the same law of cosines quadratic solving for the other leg E, so same two answers, so two answers are pairs with E and F flipped.
I do not know how in my solution to tell which quadratic answer is physically real or if they both are.
Quote: chevyThen ,my question is, Did you (how did you) get unique answers for them.
Or
Quadratic suggests two possible answers, ... which by the way I would get the same law of cosines quadratic solving for the other leg E, so same two answers, so two answers are pairs with E and F flipped.
link to original post
The only formula I needed was the quadradic formula for my latest solve. I never once needed to measure an angle, except for 60 and 90 degrees.
I'm in the early stages of writing up a solution.
In total, I must have used up about 50 pieces of paper on this problem and at least three hours. However, I can now explain the whole thing on three pages.
Quote: WizardQuote: chevyThen ,my question is, Did you (how did you) get unique answers for them.
Or
Quadratic suggests two possible answers, ... which by the way I would get the same law of cosines quadratic solving for the other leg E, so same two answers, so two answers are pairs with E and F flipped.
link to original post
The only formula I needed was the quadradic formula for my latest solve. I never once needed to measure an angle, except for 60 and 90 degrees.
I'm in the early stages of writing up a solution.
In total, I must have used up about 50 pieces of paper on this problem and at least three hours. However, I can now explain the whole thing on three pages.
link to original post
I also never needed to measure an angle, I needed law of cosines using the 60 degrees to find the last legs....and since it is solving for an adjacent side not the side opposite the angle, it gives a quadratic. That is the one I used.
c=sqrt(a^2 + b^2 - 2abcos(theta))
I knew c and b and theta, solve for "a"
Will be interested to see your full solution.
Quote: WizardHere is my solution (PDF).
link to original post
Nicely done. Very Thorough and Easy to follow. I see no mistakes. Though I have some comments
1) you calculate "f" cleanly on at top of page 5. Then you introduce "q", solve for it and do extra work to find "f" again based on "q" ending on page 6....this seems redundant....unless doing it as a "check"
2). You do use "q" to find "b". But If looking to streamline solution I think you can avoid "q".....I found "b" by looking at the "kite" piece. Draw a line to make equilateral triangle, and new line is m=k. The the right triangle with sides (m=k)=0.759836, a=0.5 , b is same as (n+p)=0.759836, e=0.5, g....so b=g=0.572145 by same Pythagorean theorem.
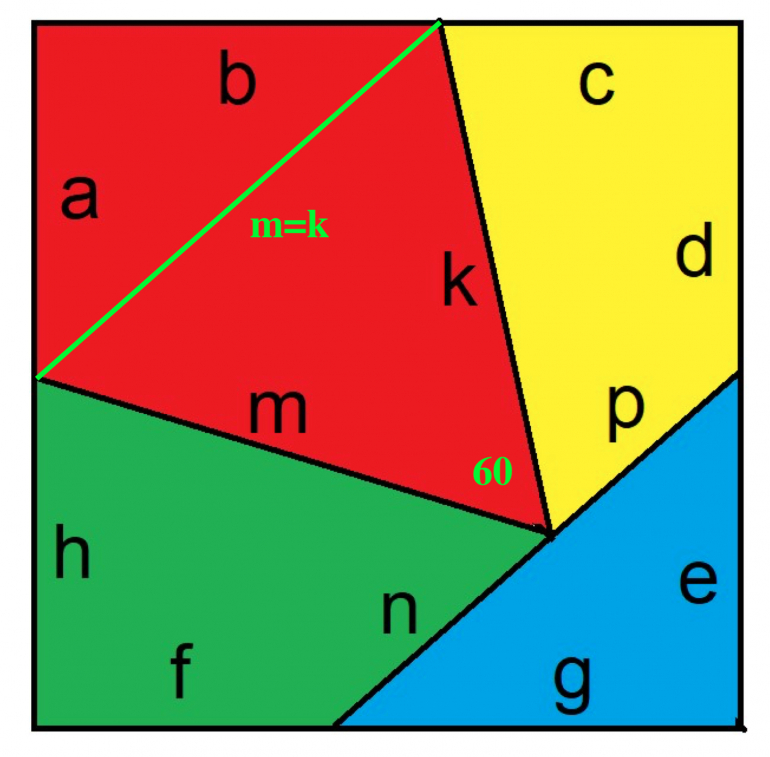
3)******Even if you keep "q" to find "b" or to find the lone remaining "length" on the pictures, the portion from bottom of page 7 seems unused?? (maybe from an old solve?)
"Next, letís solve for the side of the triangle c+q+f = c+g
We have shown already that g=b so:
c +g = c + b.
We know from the square that b+c = 1, so c+q+f = 1"
******EDIT*** I now see how you used it in right triangle with side = 1.....I guess the "q" part threw me off. In the original triangle you just need b+f = g+f = 1.
4) Again, I see no problems with your solve. FYI, I found the last two pieces by connecting the two vertices in the yellow piece (exactly what you comment on where you drop the perpendicular and can't assume new lengths are equal. by connecting the vertices, I had the right triangle with sides c,d,v........I find v by Pythagorean theorem. but then I am left with NON-right triangle with sides k,p,v and angle 60....which is where I used law of cosines as mentioned.
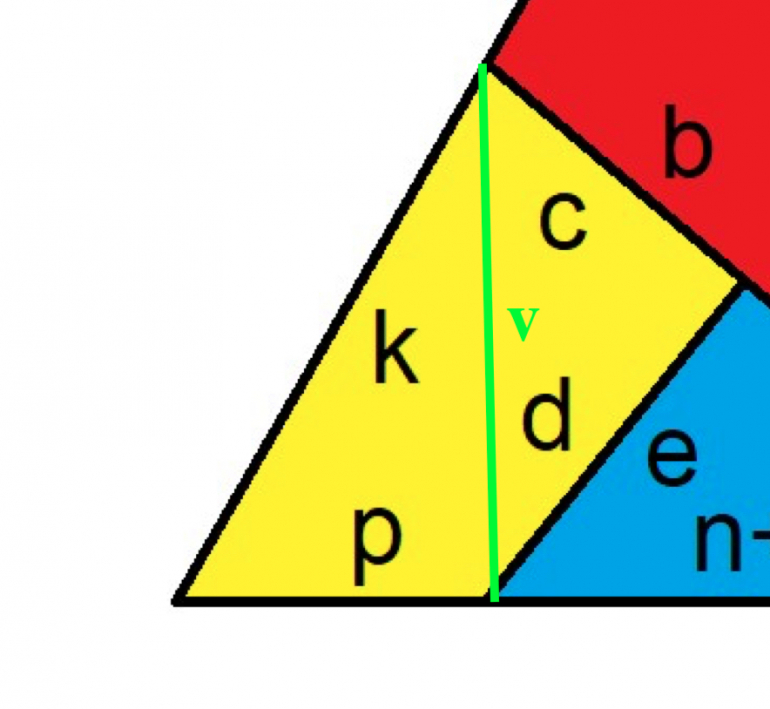
solution version 2.
Please note the attribution at the end.


