Easy math puzzles

Threads: 1520
Posts: 27118

Joined: Oct 14, 2009

March 13th, 2022 at 4:58:17 AM permalink

Quote: ThatDonGuy
Here's an easy problem that ties in with the upcoming NCAA Division I basketball tournament (your choice - men's or women's)
link to original post

I have a feeling I may not understand the question correctly, but I'm going with 65,536. This does not factor in the four teams that have to fight to even get into the 64 bracket, as I'm not sure how those rules work.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

chevy

chevy

Threads: 3
Posts: 151

Joined: Apr 15, 2011

March 13th, 2022 at 12:53:56 PM permalink

Quote: Wizard

You are correct with your updated answer! On Survivor, they allowed for two guesses.
link to original post

Then sadly I would be dead as my "updates" came in two distinct steps making my answers total 3 (i.e death)

ThatDonGuy

Threads: 122
Posts: 6738

Joined: Jun 22, 2011

March 13th, 2022 at 2:26:04 PM permalink

Quote: Wizard
Quote: ThatDonGuy
Here's an easy problem that ties in with the upcoming NCAA Division I basketball tournament (your choice - men's or women's)
link to original post

I have a feeling I may not understand the question correctly, but I'm going with 65,536. This does not factor in the four teams that have to fight to even get into the 64 bracket, as I'm not sure how those rules work.

link to original post

I think you did misunderstand. If it wasn't for any restrictions as to who made it to the Final Four, the tournament is a 64-team single elimination tournament, so there are 63 games, and, as a result, 2^63 possible brackets.

The way the "First Four" (don't call them Play-In Games - that term means something else) works is, the four weakest teams in the tournament play each other, and the four weakest teams that did not win their conference tournaments (and the automatic berth in the NCAA tournament that goes with it) play each other; the four winners advance to the "first round," which is the round of 64. There was a brief period when the NCAA called the round of 64 the "second round," as it wanted to make clear that the teams that lost in the First Four were every bit as much "NCAA tournament teams" as the eventuual national champion, but too many people complained and/or got confused, so it was changed back.

Quote: chevy

2^47???

Don't have to pick any games with the final four teams up to the final four. So # games to pick in rounds are

(28+12+4+0)=44

Then have to pick 3 more games (both semis and thee championship) since you say final four are know but NOT that you know the outcome of final four.

link to original post

Chevy's answer is correct

Each region has 15 games, but 4 of them have to be won by the team in that region chosen to be in the Final Four, so that's 2^11 possible sets of results.
Since there are four regions, that's (2^11)^4 = 2^44 sets of results where the selected four teams are in the Final Four.
For each one, there are 4 choices for the national champion, and for each of those, 2 choices for the team it beat in the final, for a total of 8 x 2^44 = 2^47 different brackets.

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 20th, 2022 at 4:16:59 PM permalink

From a deck of 52 cards, how many 5 card hands can be formed with at least 3 face cards (J, Q, K) and what is the probability you'll be dealt such a hand?

Have you tried 22 tonight? I said 22.

ThatDonGuy

Threads: 122
Posts: 6738

Joined: Jun 22, 2011

Thanked by

March 20th, 2022 at 4:33:38 PM permalink

Quote: Gialmere
From a deck of 52 cards, how many 5 card hands can be formed with at least 3 face cards (J, Q, K) and what is the probability you'll be dealt such a hand?
link to original post

There are C(12,5) = 792 hands with 5 face cards
C(12,4) x 40 = 19,800 hands with 4
C(12,3) x C(40,2) = 171,600 hands with 3
for a total of 192,192 hands
Since there are C(52,5) = 2,598,960 possible hands, the probability of being dealt one with at least 3 face cards is 44/595, or about 7.395%.

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 20th, 2022 at 7:27:06 PM permalink

Quote: ThatDonGuy

There are C(12,5) = 792 hands with 5 face cards
C(12,4) x 40 = 19,800 hands with 4
C(12,3) x C(40,2) = 171,600 hands with 3
for a total of 192,192 hands
Since there are C(52,5) = 2,598,960 possible hands, the probability of being dealt one with at least 3 face cards is 44/595, or about 7.395%.

Correct!!
----------------------------------------------

Have you tried 22 tonight? I said 22.

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 21st, 2022 at 8:00:19 AM permalink

From The Riddler...

We�re playing a game where you have to pick four whole numbers. Then I will roll four fair dice. If any two of the dice add up to any one of the numbers you picked, then you win! Otherwise, you lose.

For example, suppose you picked the numbers 2, 3, 4 and 12, and the four dice came up 1, 2, 4 and 5. Then you�d win, because two of the dice (1 and 2) add up to at least one of the numbers you picked (3).

To maximize your chances of winning, which four numbers should you pick? And what are your chances of winning?

Have you tried 22 tonight? I said 22.

Ace2

Ace2

Threads: 32
Posts: 2706

Joined: Oct 2, 2017

March 21st, 2022 at 8:28:14 AM permalink

Choose 5-8 or 6-9. 5/9 chance of winning. Basically the opposite of a field bet

It�s all about making that GTA

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 21st, 2022 at 9:05:30 AM permalink

Quote: Ace2
Choose 5-8 or 6-9. 5/9 chance of winning. Basically the opposite of a field bet

Hmm. You seem to be selecting only two numbers.

Have you tried 22 tonight? I said 22.

avianrandy

avianrandy

Threads: 8
Posts: 1858

Joined: Mar 7, 2010

Thanked by

March 21st, 2022 at 9:20:38 AM permalink

[spoiler] I think he meant 5 through 8 or 6 through 9. I. Other words 5,6,7,8 or 6,7,8,9. [/Spolier]

avianrandy

avianrandy

Threads: 8
Posts: 1858

Joined: Mar 7, 2010

March 21st, 2022 at 9:22:14 AM permalink

Tried to delete post but could not

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 21st, 2022 at 9:26:34 AM permalink

Quote: avianrandy
I think he meant 5 through 8 or 6 through 9. I. Other words 5,6,7,8 or 6,7,8,9.

Ah! Got it but, tragically, incorrect.

Have you tried 22 tonight? I said 22.

ThatDonGuy

Threads: 122
Posts: 6738

Joined: Jun 22, 2011

Thanked by

March 21st, 2022 at 9:29:34 AM permalink

Quote: Gialmere
From The Riddler...
We�re playing a game where you have to pick four whole numbers. Then I will roll four fair dice. If any two of the dice add up to any one of the numbers you picked, then you win! Otherwise, you lose.

For example, suppose you picked the numbers 2, 3, 4 and 12, and the four dice came up 1, 2, 4 and 5. Then you�d win, because two of the dice (1 and 2) add up to at least one of the numbers you picked (3).

To maximize your chances of winning, which four numbers should you pick? And what are your chances of winning?
link to original post

Choose 4, 6, 8, 10; 1264 of the 1296 possible rolls win

The only ones that lose are:
Four 1s
Three 1s and a 2, 4, or 6
Two 1s and two 6s
Three 6s and a 1, 3, or 5
Four 6s

charliepatrick

charliepatrick

Threads: 39
Posts: 3017

Joined: Jun 17, 2011

Thanked by

March 21st, 2022 at 10:00:49 AM permalink

I suspect the logic of picking 4 6 8 10 is the chances of making an even number is the opposite of only being able to make odd numbers or 2/12. Two odd rolls, not being 11, will make one of these (i.e. be a winner), and two even numbers not being 66, will also be a winner.

Thus if any die is 3 (except 3666) you can win, similarly 5 (except 5666), 2 (except 2111), 4 (except 4111). Then all combinations of 1s and/or 6s would lose: e.g. 1111 1116, 1166, 1666 and 6666. Obviously all of these can be in any order.

This gives the chances of winning 1264/1296.

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 21st, 2022 at 4:37:41 PM permalink

Quote: ThatDonGuy

Choose 4, 6, 8, 10; 1264 of the 1296 possible rolls win

The only ones that lose are:
Four 1s
Three 1s and a 2, 4, or 6
Two 1s and two 6s
Three 6s and a 1, 3, or 5
Four 6s

Quote: charliepatrick
I suspect the logic of picking 4 6 8 10 is the chances of making an even number is the opposite of only being able to make odd numbers or 2/12. Two odd rolls, not being 11, will make one of these (i.e. be a winner), and two even numbers not being 66, will also be a winner.

Thus if any die is 3 (except 3666) you can win, similarly 5 (except 5666), 2 (except 2111), 4 (except 4111). Then all combinations of 1s and/or 6s would lose: e.g. 1111 1116, 1166, 1666 and 6666. Obviously all of these can be in any order.

This gives the chances of winning 1264/1296.

Correct!!

Very good.

First off, two dice can add up to any whole number between 2 (snake eyes) and 12 (double sixes), so all four of your numbers should have come within that range. Also, whenever one of your numbers was a match, you won, so there was no point in picking the same number twice. In other words, you were picking four distinct whole numbers between 2 and 12.

Many readers knew that 7 was the most likely sum you could get from two dice, with a probability of 6/36 (or 1/6). This was followed by 6 and 8, which each had a probability of 5/36, and then 5 and 9, which each had a probability of 4/36 (or 1/9). So if you had to pick four numbers, why not pick the four most likely numbers? That meant the optimal choice of four was 5, 6, 7 and 8, or 6, 7, 8 and 9. (By symmetry, these two sets of numbers would win with equal probabilities.)

All that made sense. But it was wrong!

You could have checked it by writing out all 64 (or 1,296) cases, or preferably by checking these cases with the aid of a computer. Two dice added up to 5, 6, 7 or 8 in 1,224 of them, good for a 94.4 percent chance of victory. That sounded rather close to 100 percent, but it was possible to do even better.

The best four numbers to pick were 4, 6, 8 and 10. Two dice added up to at least one of these values in 1,264 cases, meaning your chances of victory were 97.5 percent. In the end, the most likely single sum to achieve, 7, wasn�t one of the four numbers you should have picked. What a surprising result! How was this even possible?

Your goal was to pick the four numbers that collectively covered as many of the 1,296 cases as possible. So while 7 was the single best choice, it unfortunately had significant overlap with other common sums. For example, the probability of having a pair of dice add up to 7 and a pair of dice add up to an 8 was 36.9 percent � quite a bit of overlap between those two sums. Meanwhile, the probability of having a pair add up to 6 and a pair add up to 8 was just 29.8 percent. That�s only about 7 percentage points lower, but every little bit made a difference here.

The big idea was that choosing the four most likely sums resulted in more overlap, and therefore less overall coverage of the 1,296 cases. Meanwhile, picking a set of sums that were not quite as likely individually, but more spread out across the sample space, improved your odds. Below is a sketch that is not mathematically precise, but which analogously illustrates how four smaller circles can cover a slightly greater area by having less overlap.

Solver Emma Knight took this puzzle a step further, exploring what happened when you changed the number of dice and the number of guesses. Regardless of the number of dice, if you only had one guess, you should have, of course, picked 7. With two guesses, you should have picked 6 and 7 (or, equivalently, 7 and 8). With three guesses, you should have picked 6, 7 and 8. But after that, the even numbers started to take over, leaving 7 by the wayside. As Emma pointed out, with three or more dice, you were guaranteed to have at least one even sum.

And if you were rolling at least three dice with more than six guesses, after you guessed all the even numbers, Emma suggested guessing e or 𝜋. And why not? When it comes to The Riddler, more often than not, one of those numbers shows up around here.

-------------------------------------------------------------

Have you tried 22 tonight? I said 22.

gordonm888
Administrator

gordonm888

Threads: 61
Posts: 5375

Joined: Feb 18, 2015

March 25th, 2022 at 12:49:01 PM permalink

Here's a game analysis problem, based on a bingo game structure I observed in a slot-based video game:

Bingo card has 6 columns and 6 rows with no free space square anywhere on the card. There are 120 possible numbers, your bingo card is selected randomly subject to:

First column has 6 boxes selected from 1-20
2nd column has 6 boxes selected from 21-40
...
sixth column has 6 boxes selected from 101-120.

You win a prize for each column or row that is completed on your 6x6 grid/card. Completing a diagonal is NOT considered to be a Bingo. 80 bingo numbers are drawn at random.

What are the odds that you will have zero bingos (Zero rows or columns complete) after 80 numbers have been drawn?

Full disclosure: I have not yet attempted to solve this problem. I will attempt to, but I am not the authority on when this is answered correctly.

Anyone who can provide additional info on the frequency of winning n bingos, with n=1-12 will be a math hero in my eyes.

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

ThatDonGuy

Threads: 122
Posts: 6738

Joined: Jun 22, 2011

Thanked by

March 25th, 2022 at 1:29:24 PM permalink

11 is impossible as you would need either 6 rows or 6 columns, but that requires all 36 numbers to be called, so you would have 12 bingos.

12 bingos needs all 36 numbers on the card drawn:
C(120-36, 80-36) / C(120, 80)
= C(84, 44) / C(120, 80)
= C(84, 40) / C(120, 40)
= (84 * 83 x ... x 45) / (120 x 119 x ... x 81)
= (80 x 79 x ... x 45) / (120 x 119 x ... x 85)
= 33,469,015,180 / 2,509,137,339,315,652,219, or about 1 / 74,968,962

10 requires 35 numbers, since you can only do it with 5 rows and 5 columns:
C(36,35) x C(120-36, 80-35) / C(120, 80)
= 36 x C(84, 45) / C(120, 80)
= 36 x C(84, 39) / C(120, 40)
= 36 x (84! / (45! 39!)) / (120! / (80! 40!))
= 36 x (84! 80! 40!) / (120! 45! 39!)
= 36 x (40 x 84! 80!) / (120! 45!)
= 36 x 40 x (84 x 83 x ... x 46) / (120 x 119 x ... x 81)
= 1,071,008,485,760 / 2,509,137,339,315,652,219, or about 1 / 2,342,780

Ace2

Ace2

Threads: 32
Posts: 2706

Joined: Oct 2, 2017

March 25th, 2022 at 4:22:59 PM permalink

These types of problems aren't my forte and I've never played bingo, but to get 12 bingos wouldn't the probability be:

c(80,36) / c(120,80) =~ 1 in 1,582,806,520 ?

It�s all about making that GTA

ThatDonGuy

Threads: 122
Posts: 6738

Joined: Jun 22, 2011

March 25th, 2022 at 7:05:43 PM permalink

Quote: Ace2
These types of problems aren't my forte and I've never played bingo, but to get 12 bingos wouldn't the probability be:

c(80,36) / c(120,80) =~ 1 in 1,582,806,520 ?

link to original post

No. You're right about there being C(120,80) sets of drawn numbers, but look at it this way:
In order to get 12 bingos, all 36 of your numbers have to be drawn.
Color the 36 balls on your card red, and the other 84 white.
Of the 80 that are drawn, all 36 red ones need to be drawn, which means that 44 of the 84 white ones will be drawn as well.

ThatDonGuy

Threads: 122
Posts: 6738

Joined: Jun 22, 2011

March 27th, 2022 at 4:02:09 PM permalink

After some serious number crunching (doing a brute force computing search), I get the following probabilities for each number of lines:

0 lines: 20,399,310,508,737,822,613,691,645 / 54,208,514,626,416,667,373,209,017 (1 / 2.657)
1 line: 453,138,748,079,790,278,790,802,600 / 1,246,795,836,407,583,349,583,807,391 (1 / 2.751)
2 lines: 75,184,281,240,179,546,107,280,550 / 415,598,612,135,861,116,527,935,797 (1 / 5.528)
3 lines: 74,961,880,766,219,254,839,487,700 / 1,246,795,836,407,583,349,583,807,391 (1 / 16.63)
4 lines: 19,111,256,934,190,578,133,923,260 / 1,246,795,836,407,583,349,583,807,391 (1 / 65.24)
5 lines: 22,485,961,213,854,457,920,528 / 7,044,044,273,489,171,466,575,183 (1 / 313.26)
6 lines: 4,112,990,939,009,607,535,740 / 7,044,044,273,489,171,466,575,183 (1 / 1712.6)
7 lines: 12,492,941,476,251,446,600 / 132,906,495,726,210,782,388,211 (1 / 10,639)
8 lines: 41,224,371,704,971,650 / 2,712,377,463,800,220,048,739 (1 / 65,795)
9 lines: 104,423,327,361,600 / 57,710,158,804,260,001,037 (1 / 552,656)
10 lines: 1,071,008,485,760 / 2,509,137,339,315,652,219 (1 / 2,342,780)
11 lines: 0
12 lines: 33,469,015,180 / 2,509,137,339,315,652,219 (1 / 74,968,962)

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 28th, 2022 at 8:07:06 AM permalink

Here's a classic puzzle that's harder than it looks...

A grassy field is in the shape of a circle of radius 100m and is enclosed by a circular fence.

A goat is attached by a rope to a hook, at a fixed point on the fence.

To stop the goat getting too fat, the farmer wants to make sure that it can only reach half of the grass in the field.

How long should the rope be?

Have you tried 22 tonight? I said 22.

ThatDonGuy

Threads: 122
Posts: 6738

Joined: Jun 22, 2011

March 28th, 2022 at 10:32:49 AM permalink

Is there an "exact" value for this? I can come up with a solution, but it involves a bit of trigonometry in the answer.

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 28th, 2022 at 10:39:24 AM permalink

Quote: ThatDonGuy

Is there an "exact" value for this? I can come up with a solution, but it involves a bit of trigonometry in the answer.

link to original post

An approximation rounding the rope to the nearest meter in length is acceptable.

Have you tried 22 tonight? I said 22.

Ace2

Ace2

Threads: 32
Posts: 2706

Joined: Oct 2, 2017

March 28th, 2022 at 10:55:19 AM permalink

The weather channel app on my phone listed a 100% chance of rain this morning but it never did rain...now the sky is clearing and there is no more forecast for rain today

What are the odds of something with a 100% chance not occurring?

It�s all about making that GTA

ThatDonGuy

Threads: 122
Posts: 6738

Joined: Jun 22, 2011

Thanked by

March 28th, 2022 at 11:07:21 AM permalink

Quote: Gialmere
Quote: ThatDonGuy

Is there an "exact" value for this? I can come up with a solution, but it involves a bit of trigonometry in the answer.

link to original post

An approximation rounding the rope to the nearest meter in length is acceptable.

link to original post

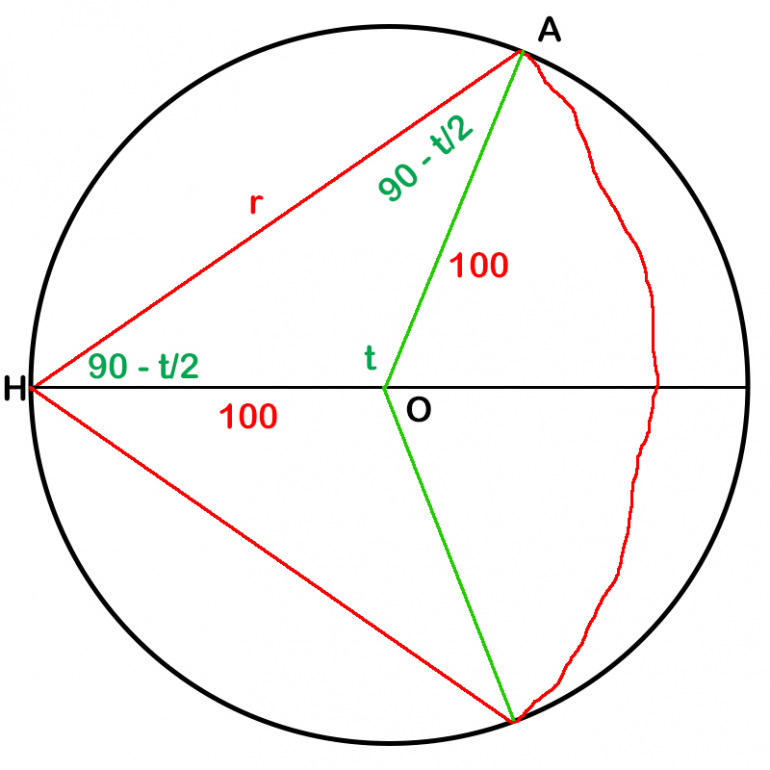
Sorry about that red arc on the right; you would think Adobe Photoshop Elements would include an easy way to draw an arc.

Let O be the center of the field, H be the point where the rope is hooked to the fence,
and A be one of the two points on the fence that is the length of the rope away from H.
Let r be the length of the rope; HA = r.
The field is symmetric with respect to the diameter that includes H, so only half of the value will be calculated, and the result multiplied by 2 to obtain the final result.

One formula for the area of a triangle = 1/2 the product of the lengths of two sides * the sine of the angle where they meet
The area covered in half of the field = PI r^2 * (90 - t/2) / 360 + PI * 100^2 * t / 360 - 1/2 * 100^2 sin t
Bisect AH; sin (t / 2) = (r / 2) / 100 = r / 200
t = 2 arcsin (r / 200)

The total area covered = 2 (PI r^2 * (90 - t/2) / 360 + PI * 100^2 * t / 360 - 1/2 * 100^2 sin t)
= 2 (PI r^2 * (90 - arcsin(r / 200)) / 360 + PI * 500 arcsin(r / 200) / 9 - 5000 sin t)
= PI r^2 * (90 - arcsin(r / 200)) / 180 + PI * 1000 arcsin(r / 200) / 9 - 10,000 sin t

Since this equals half of the area of the field, which is 5000 PI:

5000 PI = PI r^2 * (90 - arcsin(r / 200)) / 180 + PI * 1000 arcsin(r / 200) / 9 - 10,000 sin t
5000 = r^2 * (90 - arcsin(r / 200)) / 180 + 1000 arcsin(r / 200) / 9 - 10,000 / PI * sin t

sin t = sin (2 * t/2) = 2 sin (t/2) cos (t/2) = 2 * r / 200 * sqrt(1 - r^2 / 40,000) = r sqrt(1 - r^2 / 40,000) / 100

5000 = r^2 * (90 - arcsin(r / 200)) / 180 + 1000 arcsin(r / 200) / 9 - 100 / PI * r sqrt(1 - r^2 / 40,000)

The length of the rope = about 116 m

aceside

aceside

Threads: 2
Posts: 591

Joined: May 14, 2021

March 28th, 2022 at 12:06:20 PM permalink

This can be solved by using polar equations.

The polar equation of the larger circle is
r=x.

The polar equation of the smaller circle is
r=200 cos(theta).

Solving the set of two equations to find the intersection points, and thus the limits of integration.

Using the polar equations and the intersection points to do an area integration, we should find it.

ThatDonGuy

Threads: 122
Posts: 6738

Joined: Jun 22, 2011

March 28th, 2022 at 12:31:48 PM permalink

Quote: aceside
This can be solved by using polar equations.

The polar equation of the larger circle is
r=x.

The polar equation of the smaller circle is
r=200 cos(theta).

Solving the set of two equations to find the intersection points, and thus the limits of integration.

Using the polar equations and the intersection points to do an area integration, we should find it.
link to original post

But doesn't the range of the integration depend on the length of the rope?

unJon

unJon

Threads: 16
Posts: 4808

Joined: Jul 1, 2018

March 28th, 2022 at 12:35:01 PM permalink

Quote: ThatDonGuy
Quote: Gialmere
Quote: ThatDonGuy

Is there an "exact" value for this? I can come up with a solution, but it involves a bit of trigonometry in the answer.

link to original post

An approximation rounding the rope to the nearest meter in length is acceptable.

link to original post

Sorry about that red arc on the right; you would think Adobe Photoshop Elements would include an easy way to draw an arc.

Let O be the center of the field, H be the point where the rope is hooked to the fence,
and A be one of the two points on the fence that is the length of the rope away from H.
Let r be the length of the rope; HA = r.
The field is symmetric with respect to the diameter that includes H, so only half of the value will be calculated, and the result multiplied by 2 to obtain the final result.

One formula for the area of a triangle = 1/2 the product of the lengths of two sides * the sine of the angle where they meet
The area covered in half of the field = PI r^2 * (90 - t/2) / 360 + PI * 100^2 * t / 360 - 1/2 * 100^2 sin t
Bisect AH; sin (t / 2) = (r / 2) / 100 = r / 200
t = 2 arcsin (r / 200)

The total area covered = 2 (PI r^2 * (90 - t/2) / 360 + PI * 100^2 * t / 360 - 1/2 * 100^2 sin t)
= 2 (PI r^2 * (90 - arcsin(r / 200)) / 360 + PI * 500 arcsin(r / 200) / 9 - 5000 sin t)
= PI r^2 * (90 - arcsin(r / 200)) / 180 + PI * 1000 arcsin(r / 200) / 9 - 10,000 sin t

Since this equals half of the area of the field, which is 5000 PI:

5000 PI = PI r^2 * (90 - arcsin(r / 200)) / 180 + PI * 1000 arcsin(r / 200) / 9 - 10,000 sin t
5000 = r^2 * (90 - arcsin(r / 200)) / 180 + 1000 arcsin(r / 200) / 9 - 10,000 / PI * sin t

sin t = sin (2 * t/2) = 2 sin (t/2) cos (t/2) = 2 * r / 200 * sqrt(1 - r^2 / 40,000) = r sqrt(1 - r^2 / 40,000) / 100

5000 = r^2 * (90 - arcsin(r / 200)) / 180 + 1000 arcsin(r / 200) / 9 - 100 / PI * r sqrt(1 - r^2 / 40,000)

The length of the rope = about 116 m

link to original post

Your drawing is funny. Note that the rope should bisect the circle at points that are to the left of the center of the circle, not the right of the center of the circle.

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 28th, 2022 at 4:45:51 PM permalink

Quote: ThatDonGuy

Sorry about that red arc on the right; you would think Adobe Photoshop Elements would include an easy way to draw an arc.

Let O be the center of the field, H be the point where the rope is hooked to the fence,
and A be one of the two points on the fence that is the length of the rope away from H.
Let r be the length of the rope; HA = r.
The field is symmetric with respect to the diameter that includes H, so only half of the value will be calculated, and the result multiplied by 2 to obtain the final result.

One formula for the area of a triangle = 1/2 the product of the lengths of two sides * the sine of the angle where they meet
The area covered in half of the field = PI r^2 * (90 - t/2) / 360 + PI * 100^2 * t / 360 - 1/2 * 100^2 sin t
Bisect AH; sin (t / 2) = (r / 2) / 100 = r / 200
t = 2 arcsin (r / 200)

The total area covered = 2 (PI r^2 * (90 - t/2) / 360 + PI * 100^2 * t / 360 - 1/2 * 100^2 sin t)
= 2 (PI r^2 * (90 - arcsin(r / 200)) / 360 + PI * 500 arcsin(r / 200) / 9 - 5000 sin t)
= PI r^2 * (90 - arcsin(r / 200)) / 180 + PI * 1000 arcsin(r / 200) / 9 - 10,000 sin t

Since this equals half of the area of the field, which is 5000 PI:

5000 PI = PI r^2 * (90 - arcsin(r / 200)) / 180 + PI * 1000 arcsin(r / 200) / 9 - 10,000 sin t
5000 = r^2 * (90 - arcsin(r / 200)) / 180 + 1000 arcsin(r / 200) / 9 - 10,000 / PI * sin t

sin t = sin (2 * t/2) = 2 sin (t/2) cos (t/2) = 2 * r / 200 * sqrt(1 - r^2 / 40,000) = r sqrt(1 - r^2 / 40,000) / 100

5000 = r^2 * (90 - arcsin(r / 200)) / 180 + 1000 arcsin(r / 200) / 9 - 100 / PI * r sqrt(1 - r^2 / 40,000)

The length of the rope = about 116 m

link to original post

Correct!!

Well done.

-------------------------------------------------------------------------

Have you tried 22 tonight? I said 22.

Wizard
Administrator

Threads: 1520
Posts: 27118

Joined: Oct 14, 2009

March 28th, 2022 at 5:21:31 PM permalink

My answer is 115.8728598 meters.

I got it with basic geometry and trial and error.

If this is correct, I'll work on a closed form solution, but am afraid already it will be a mess.

What is the term for the section of a circle cut off by a chord?

p.s. Dang, I see Don beat me to the punch. At least my answer looks right.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Wizard
Administrator

Threads: 1520
Posts: 27118

Joined: Oct 14, 2009

March 28th, 2022 at 6:53:07 PM permalink

Quote: Wizard
What is the term for the section of a circle cut off by a chord?
link to original post

To answer my own question -- a segment.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Wizard
Administrator

Threads: 1520
Posts: 27118

Joined: Oct 14, 2009

March 28th, 2022 at 7:26:15 PM permalink

I plan to make an Ask the Wizard question for this one. Here is a diagram I plan to use, should anyone wish to use it as a reference.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 30th, 2022 at 8:48:53 AM permalink

Here's an easy one...

'Decimals? Bah! That may be how math works on your stupid planet Earth, but here on Mars everyone knows one half of five is three exactly,' grumbled Jim the Martian, as if he had just heard the most ridiculous thing in his life.

If one half of five is three on Mars, and assuming this strange proportion is the rule, what is one third of ten?

Have you tried 22 tonight? I said 22.

chevy

chevy

Threads: 3
Posts: 151

Joined: Apr 15, 2011

Thanked by

March 30th, 2022 at 9:20:35 AM permalink

4??

3 = 5/2
so
1/3 = 2/5

and

(1/3)*10 = (2/5)*10 = 4???

charliepatrick

charliepatrick

Threads: 39
Posts: 3017

Joined: Jun 17, 2011

Thanked by

March 30th, 2022 at 9:50:07 AM permalink

I'm not convinced but if 3+3=5 then 3+3+3+3=10 (although it isn't obvious why 5+5 might not be less) so 3/3+3/3+3/3+3/3=10/3=4.

Wizard
Administrator

Threads: 1520
Posts: 27118

Joined: Oct 14, 2009

Thanked by

March 30th, 2022 at 11:15:44 AM permalink

I'm not sure I understand the question correctly, but I'm going with 4.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 30th, 2022 at 5:55:34 PM permalink

Quote: chevy

4??

3 = 5/2
so
1/3 = 2/5

and

(1/3)*10 = (2/5)*10 = 4???

link to original post

Quote: charliepatrick
I'm not convinced but if 3+3=5 then 3+3+3+3=10 (although it isn't obvious why 5+5 might not be less) so 3/3+3/3+3/3+3/3=10/3=4.

link to original post

Quote: Wizard
I'm not sure I understand the question correctly, but I'm going with 4.

link to original post

Correct!!

We know that according to Martian rules, 1/2 * 5 = 3 (Here on Earth, the real answer is 2.5). We want to know what 1/3 * 10 would be using the same wonky proportions.

--Try setting up the problem like so: 1/2 * 5 = 3.
--But we want to know about thirds. So multiply both sides of the equation by 1/3. You will end up with 1/6 * 5 = 1. Getting there!
--Turn that 1/6 into 1/3 by multiplying both sides by two and you will end up with 1/3 * 5 = 2. So, one third of five is two�
--Now all you have to do is double the whole thing (multiply both sides by two again) to figure out what one third of ten would be. (It is, of course, four.)

--------------------------------------------------------------

Bad Jokes

...they should send me up there with a golf club and a ball.

It seems it has received signals from Hot MILFs in it's area.

Have you tried 22 tonight? I said 22.

rsactuary

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

March 30th, 2022 at 7:41:17 PM permalink

Here's an interesting problem that i saw floating on the interwebs. I admit I never would have figured this out.

Problem: You have a calculator that has broken multiply and divide buttons. The only operations available to you are addition, subtraction and the reciprocal function.

You are given two numbers. X and Y. Determine a way that you can find X*Y (x times y) on this calculator.

Dieter
Administrator

Dieter

Threads: 16
Posts: 6107

Joined: Jul 23, 2014

March 30th, 2022 at 8:43:14 PM permalink

Quote: rsactuary
Here's an interesting problem that i saw floating on the interwebs. I admit I never would have figured this out.

Problem: You have a calculator that has broken multiply and divide buttons. The only operations available to you are addition, subtraction and the reciprocal function.

You are given two numbers. X and Y. Determine a way that you can find X*Y (x times y) on this calculator.
link to original post

Take the reciprocal of (1/x)-(1/y).

In keypresses, x reciprocal - y reciprocal = reciprocal.

If your X and Y are entered wrong way round, you may get a negative number when it should be positive. Such are the perils of using a broken calculator.

May the cards fall in your favor.

rsactuary

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

March 30th, 2022 at 9:21:36 PM permalink

Quote: Dieter
Quote: rsactuary
Here's an interesting problem that i saw floating on the interwebs. I admit I never would have figured this out.

Problem: You have a calculator that has broken multiply and divide buttons. The only operations available to you are addition, subtraction and the reciprocal function.

You are given two numbers. X and Y. Determine a way that you can find X*Y (x times y) on this calculator.
link to original post

Take the reciprocal of (1/x)-(1/y).

In keypresses, x reciprocal - y reciprocal = reciprocal.

If your X and Y are entered wrong way round, you may get a negative number when it should be positive. Such are the perils of using a broken calculator.

link to original post

On the right track, but no

Dieter
Administrator

Dieter

Threads: 16
Posts: 6107

Joined: Jul 23, 2014

March 30th, 2022 at 9:35:03 PM permalink

Quote: rsactuary

On the right track, but no
link to original post

Yes, I think I saw some cases that might not work.

Although why one would on a calculator without an enter key puzzles me.

May the cards fall in your favor.

charliepatrick

charliepatrick

Threads: 39
Posts: 3017

Joined: Jun 17, 2011

March 30th, 2022 at 11:46:17 PM permalink

1/x+1/y = (y+x)/xy, so xy = (y+x)/(1/x + 1/y). You can work the numerator and denominator but not do the division.

Example 2.4 * 3.6 = 6 / (.4166+.2777) = 6 * 1.44. That's back to the original problem of multiplying two numbers!

ThatDonGuy

Threads: 122
Posts: 6738

Joined: Jun 22, 2011

March 31st, 2022 at 6:40:25 AM permalink

Quote: Dieter
Quote: rsactuary
Here's an interesting problem that i saw floating on the interwebs. I admit I never would have figured this out.

Problem: You have a calculator that has broken multiply and divide buttons. The only operations available to you are addition, subtraction and the reciprocal function.

You are given two numbers. X and Y. Determine a way that you can find X*Y (x times y) on this calculator.
link to original post

Take the reciprocal of (1/x)-(1/y).

In keypresses, x reciprocal - y reciprocal = reciprocal.

If your X and Y are entered wrong way round, you may get a negative number when it should be positive. Such are the perils of using a broken calculator.

link to original post

1 / (1 / x - 1 / y) = xy / (y - x), but where do you go from there? You can't multiply that by (y - x) as the multiply key is broken, remember?

Wizard
Administrator

Threads: 1520
Posts: 27118

Joined: Oct 14, 2009

March 31st, 2022 at 6:48:12 AM permalink

I would first take the smaller number and break it into powers of 2. For example, let's say a = 53 and b = 69.

a = 32+16+4+1

Then, keep doubling a until you can put it together by it's powers of 2:

c = a+a = 138
d = c+c = 276
e = d+d = 552
f = e+e = 1104
g = f+f = 2208

In our example, a*b = b + d + f + g = 3657

I would first take the smaller number and break it into powers of 2. For example, let's say a = 53 and b = 69.

a = 32+16+4+1

Then, keep doubling a until you can put it together by it's powers of 2:

c = b+b = 138
d = c+c = 276
e = d+d = 552
f = e+e = 1104
g = f+f = 2208

In our example, a*b = b + d + f + g = 3657

Last edited by: Wizard on Mar 31, 2022

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Dieter
Administrator

Dieter

Threads: 16
Posts: 6107

Joined: Jul 23, 2014

March 31st, 2022 at 6:49:42 AM permalink

Quote: ThatDonGuy
Quote: Dieter
Quote: rsactuary
Here's an interesting problem that i saw floating on the interwebs. I admit I never would have figured this out.

Problem: You have a calculator that has broken multiply and divide buttons. The only operations available to you are addition, subtraction and the reciprocal function.

You are given two numbers. X and Y. Determine a way that you can find X*Y (x times y) on this calculator.
link to original post

Take the reciprocal of (1/x)-(1/y).

In keypresses, x reciprocal - y reciprocal = reciprocal.

If your X and Y are entered wrong way round, you may get a negative number when it should be positive. Such are the perils of using a broken calculator.

link to original post

1 / (1 / x - 1 / y) = xy / (y - x), but where do you go from there? You can't multiply that by (y - x) as the multiply key is broken, remember?

link to original post

It works great if x-y=1.

May the cards fall in your favor.

rsactuary

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

March 31st, 2022 at 7:05:00 AM permalink

Quote: Wizard

I would first take the smaller number and break it into powers of 2. For example, let's say a = 53 and b = 69.

a = 32+16+4+1

Then, keep doubling a until you can put it together by it's powers of 2:

c = a+a = 138
d = c+c = 276
e = d+d = 552
f = e+e = 1104
g = f+f = 2208

In our example, a*b = b + d + f + g = 3657

link to original post

Not sure what I'm missing but a+a doesn't equal 138 in my head. Your solution is not the one I saw with the question and doesn't your solution really rely on you knowing the answer beforehand?

Wizard
Administrator

Threads: 1520
Posts: 27118

Joined: Oct 14, 2009

March 31st, 2022 at 7:45:41 AM permalink

Quote: rsactuary
Not sure what I'm missing but a+a doesn't equal 138 in my head. Your solution is not the one I saw with the question and doesn't your solution really rely on you knowing the answer beforehand?
link to original post

You don't need to be sarcastic. I had a typo. I meant to say b+b=138. No, my method doesn't rely on know the answer beforehand. If you replace the line c=a+a=138 with c=b+b=138, tell me where my method does not meet your rules.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ThatDonGuy

Threads: 122
Posts: 6738

Joined: Jun 22, 2011

March 31st, 2022 at 8:07:36 AM permalink

Quote: Wizard

I would first take the smaller number and break it into powers of 2. For example, let's say a = 53 and b = 69.

a = 32+16+4+1

Then, keep doubling a until you can put it together by it's powers of 2:

c = a+a = 138
d = c+c = 276
e = d+d = 552
f = e+e = 1104
g = f+f = 2208

In our example, a*b = b + d + f + g = 3657

I would first take the smaller number and break it into powers of 2. For example, let's say a = 53 and b = 69.

a = 32+16+4+1

Then, keep doubling a until you can put it together by it's powers of 2:

c = b+b = 138
d = c+c = 276
e = d+d = 552
f = e+e = 1104
g = f+f = 2208

In our example, a*b = b + d + f + g = 3657

link to original post

You are assuming that at least one of the numbers is an integer. In that case, this solution is equally valid:

Let y be an integer.
Enter x + x + x + ... + x, where there are y x's.

I am working under the assumption that neither x nor y are integers, nor can I assume that either is an integer divided by a positive power of 10.

Wizard
Administrator