Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
Quote: Ace2Iíve never played repeater, but Iím asking what is the chance of rolling (at least) two 2s, three 3s, four 4s etc before rolling a 7.
Did you mean two 2s, three 3s, and so on, through twelve 12s, or just two of each?
Just rolling 12 12s before a 7 is (1/7)^12, or about 1 in 13.84 billion.
What is the over/under on how many posts before somebody's reply mentions "18 Yos"?
Quote: Ace2Going by the repeater rules, a 12 is like a 2 (must be repeated twice), an 11 three times etc
I get about 1 in 185,100
Question for the calculus boffins: I know the probability of not rolling a 2 in time t is 1 / e^(t/36), but what is the probability of not rolling a 2 at least twice in time t?
I agree with that estimate. The exact answer is:Quote: ThatDonGuyI get about 1 in 185,100
228,296,650,211,142,223,842,235,175,926,562,819,565,310,943,733,017,295,518,075,498,704,612,736,041,415,500,474,174,790,373,335,885,790,742,403,815,919,759,376,329,015,547,908,450,301,690,458,558,920,417,797,769,549,693,735,380,351,101,698,849,553,401,942,470,326,707,347,462,797,442,543,279,964,206,576,929,140,810,851,250,499,537,038,847,980,599,155,971,380,821,671,855,091,570,073,172,919,198,633,489/
42,257,698,361,772,482,521,904,922,230,217,663,263,013,990,621,490,761,617,970,468,605,585,232,439,497,131,274,911,233,268,994,399,835,192,106,236,921,993,503,595,172,067,323,864,679,436,391,989,136,613,954,326,164,471,151,500,091,945,731,257,099,763,259,926,492,493,587,351,085,501,547,293,599,982,107,240,564,537,220,360,657,324,137,622,979,804,472,478,269,440,000,000,000,000,000,000,000,000,000,000,000,000
Does anyone want more time before I post the method?
Quote: Ace2I agree with that estimate. The exact answer is:
228,296,650,211,142,223,842,235,175,926,562,819,565,310,943,733,017,295,518,075,498,704,612,736,041,415,500,474,174,790,373,335,885,790,742,403,815,919,759,376,329,015,547,908,450,301,690,458,558,920,417,797,769,549,693,735,380,351,101,698,849,553,401,942,470,326,707,347,462,797,442,543,279,964,206,576,929,140,810,851,250,499,537,038,847,980,599,155,971,380,821,671,855,091,570,073,172,919,198,633,489/
42,257,698,361,772,482,521,904,922,230,217,663,263,013,990,621,490,761,617,970,468,605,585,232,439,497,131,274,911,233,268,994,399,835,192,106,236,921,993,503,595,172,067,323,864,679,436,391,989,136,613,954,326,164,471,151,500,091,945,731,257,099,763,259,926,492,493,587,351,085,501,547,293,599,982,107,240,564,537,220,360,657,324,137,622,979,804,472,478,269,440,000,000,000,000,000,000,000,000,000,000,000,000
Does anyone want more time before I post the method?
That is a surprising number of zeros at the end of the denominator. Are you sure it didnít round that?
Yes Iím pretty sure. Even if it was rounded, thereís still about 300 significant digitsQuote: unJonThat is a surprising number of zeros at the end of the denominator. Are you sure it didnít round that?
(1 - ((1 - ((5x/36)^5/120 + (5x/36)^4/24 + (5x/36)^3/6 + (5x/36)^2/2 + (5x/36) + 1) * e^(-5x/36)) * (1 - ((x/9)^4/24 + (x/9)^3/6 + (x/9)^2/2 + (x/9) + 1) * e^(-x/9)) * (1 - ((x/12)^3/6 + (x/12)^2/2 + (x/12) + 1) * e^(-x/12)) * (1 - ((x/18)^2/2 + (x/18) + 1) * e^(-x/18)) * (1 - ((x/36) + 1) * e^(-x/36)))^2) * e^(-x/6) * 1/6 dx
The integral evaluates the probabilities at all time (x) that at least one repeater bet has not been won and a seven has not been rolled. Multiply by 1/6 for the chance that the next roll is a seven, causing the bet to lose.
Quote: Ace2The answer is 1 minus the integral from zero to infinity of:
(1 - ((1 - ((5x/36)^5/120 + (5x/36)^4/24 + (5x/36)^3/6 + (5x/36)^2/2 + (5x/36) + 1) * e^(-5x/36)) * (1 - ((x/9)^4/24 + (x/9)^3/6 + (x/9)^2/2 + (x/9) + 1) * e^(-x/9)) * (1 - ((x/12)^3/6 + (x/12)^2/2 + (x/12) + 1) * e^(-x/12)) * (1 - ((x/18)^2/2 + (x/18) + 1) * e^(-x/18)) * (1 - ((x/36) + 1) * e^(-x/36)))^2) * e^(-x/6) * 1/6 dx
The integral evaluates the probabilities at all time (x) that at least one repeater bet has not been won and a seven has not been rolled. Multiply by 1/6 for the chance that the next roll is a seven, causing the bet to lose.
I assume that ((5x/36)^5/120 + (5x/36)^4/24 + (5x/36)^3/6 + (5x/36)^2/2 + (5x/36) + 1) * e^(-5x/36) is the probability of not rolling a 6 at least 6 times in time x. How did you work that out?
Quote: unJonQuote: Ace2I agree with that estimate. The exact answer is:
228,296,650,211,142,223,842,235,175,926,562,819,565,310,943,733,017,295,518,075,498,704,612,736,041,415,500,474,174,790,373,335,885,790,742,403,815,919,759,376,329,015,547,908,450,301,690,458,558,920,417,797,769,549,693,735,380,351,101,698,849,553,401,942,470,326,707,347,462,797,442,543,279,964,206,576,929,140,810,851,250,499,537,038,847,980,599,155,971,380,821,671,855,091,570,073,172,919,198,633,489/
42,257,698,361,772,482,521,904,922,230,217,663,263,013,990,621,490,761,617,970,468,605,585,232,439,497,131,274,911,233,268,994,399,835,192,106,236,921,993,503,595,172,067,323,864,679,436,391,989,136,613,954,326,164,471,151,500,091,945,731,257,099,763,259,926,492,493,587,351,085,501,547,293,599,982,107,240,564,537,220,360,657,324,137,622,979,804,472,478,269,440,000,000,000,000,000,000,000,000,000,000,000,000
That is a surprising number of zeros at the end of the denominator. Are you sure it didnít round that?
My Markov chain result is the same, right down to the same number of zeroes in the denominator.
Itís just Poisson.Quote: ThatDonGuyI assume that ((5x/36)^5/120 + (5x/36)^4/24 + (5x/36)^3/6 + (5x/36)^2/2 + (5x/36) + 1) * e^(-5x/36) is the probability of not rolling a 6 at least 6 times in time x. How did you work that out?
.
e^(-5x/36) * (5x/36)^5/120 is the chance of rolling five 6s in time x, e^(-5x/36) * (5x/36)^4/24 is the chance of rolling four 6s in time x, etc. Sum these for values 0 - 5 and thatís the probability of rolling less than six 6ís.
Rephrase: All fire bet winners will have won at least six points before sevening out. When someone wins the fire bet, what is the expected number of total points won?Quote: Ace2When someone wins the Fire Bet, how many total pass bets will they have won, on average?
Quote: Ace2Rephrase: All fire bet winners will have won at least six points before sevening out. When someone wins the fire bet, what is the expected number of total points won?
Tough one!
I tried a Markov chain, where the probability of making a particular point was in proportion to establishing that point, but I got something like 17 - while a simulation returns around 7.4.
Presumably, it's low because the higher the number of points that are established, the more likely it is that you will seven out.
A total of seven is rolled
A total of three is rolled 3x
A total of five is rolled 5x
A total of nine is rolled 5x
A total of 11 is rolled 3x
What is the probability the ending event is any of the last four listed?
Quote: Ace21 - 30026163533 / 31381059609 =~ 4.32%
How about that - I actually managed to figure out the Poisson-based method for this one:
Only rolls of 3, 5, 7, 9, and 11 are concerned here, so they have probabilities of 1/9, 2/9, 1/3, 2/9, and 1/9 respectively
Note that all of these are derivatives from 0 to positive infinity, dx
In time x:
P(< 3 3s) = P(< 3 11s) = e^(-x/9) * (1 + x/9 + (x/9)^2 / 2)
P(< 5 5s) = P(< 5 9s) = e^(-2x/9) * (1 + 2x/9 + (2x/9)^2 / 2 + (2x/9)^3 / 6) + (2x/9)^4 / 24)
P(no 7s) = e^(-x/3)
P(all five) = e^(-x/3) * (e^(-x/9) * (1 + x/9 + (x/9)^2 / 2) * e^(-2x/9) * (1 + 2x/9 + (2x/9)^2 / 2 + (2x/9)^3 / 6) + (2x/9)^4 / 24))^2
= e^(-x) * ((1 + x/9 + (x/9)^2 / 2) * (1 + 2x/9 + (2x/9)^2 / 2 + (2x/9)^3 / 6 + (2x/9)^4 / 24))^2
P(rolling a 7 first) = P(all five, and then a 7) = e^(-x) * ((1 + x/9 + (x/9)^2 / 2) * (1 + 2x/9 + (2x/9)^2 / 2 + (2x/9)^3 / 6 + (2x/9)^4 / 24))^2
Quote: Ace21 - 30026163533 / 31381059609 =~ 4.32%
I agree! I show a brief solution of all the difficult Repeater Bet Plus bets here.
The exact answer is:Quote: Ace2Rephrase: All fire bet winners will have won at least six points before sevening out. When someone wins the fire bet, what is the expected number of total points won?
51,194,997,861,765,388,097,526,966,955,556,874,130,535,332,020,426,690,698,014,074,625,318,137,025,571,849,255 /
6,923,708,358,532,324,948,598,712,995,072,892,018,553,301,246,118,708,475,186,839,062,876,563,686,189,522,216
=~7.39415862291138014289 average total points won
Would any of our calculus ninjas like more time before I post the solution?
Quote: Ace2The exact answer is:
51,194,997,861,765,388,097,526,966,955,556,874,130,535,332,020,426,690,698,014,074,625,318,137,025,571,849,255 /
6,923,708,358,532,324,948,598,712,995,072,892,018,553,301,246,118,708,475,186,839,062,876,563,686,189,522,216
=~7.39415862291138014289 average total points won
Would any of our calculus ninjas like more time before I post the solution?
Don't look at me; I'm surprised there is a rational number solution - I thought it would end up being an infinite series (calculate the probabilities of winning with 6, 7, 8, 9, ... points, then add them together).
If you know how to calculate the house edge of the fire bet using calculus, then you already have almost the entire solution. Itís just a slightly different approach
Quote: Ace2Rephrase: All fire bet winners will have won at least six points before sevening out. When someone wins the fire bet, what is the expected number of total points won?
First you calculate the probability of winning the fire bet. Though this has already been posted, I'll recap as follows. Out of 3,960 possible outcomes/decisions, there are 165 ways to win a 4 (same to win a 10), 264 ways to win a 5 (same to win a 9), 375 ways to win a 6 (same to win an 8) and 2,352 ways to seven out.
The "indirect" way (counting all winning strings regardless of when they win) to calculate the edge is by integrating the following from zero to infinity:
((1 - e^(-165x/3960))^2 * (1 - e^(-264x/3960))^2 * (1 - e^(-375x/3960))^2 * e^(-2352x/3960) * 2352/3960 dx
The "direct" way (counting all strings at the exact time they win) to calculate the edge is by integrating the following from zero to infinity:
((1 - e^(-165x/3960))^2 * (1 - e^(-264x/3960))^2 * (1 - e^(-375x/3960)) * e^(-375x/3960) * 375/3960 + (1 - e^(-165x/3960))^2 * ( 1 - e^(-375x/3960))^2 * ( 1 -e^(-264x/3960)) * e^(-264x/3960) * 264/3960 + (1 - e^(-375x/3960))^2 * (1 - e^(-264x/3960))^2 * (1 - e^(-165x/3960)) * e^(-165x/3960) * 165/3960) * e^(-2352x/3960) * 2 dx
Both methods give the same probability of winning of ~0.0001624.
Next, take the same direct integral from zero to infinity but also multiply by x. Using the indirect integral will not give the correct answer. So :
((1 - e^(-165x/3960))^2 * (1 - e^(-264x/3960))^2 * (1 - e^(-375x/3960)) * e^(-375x/3960) * 375/3960 + (1 - e^(-165x/3960))^2 * ( 1 - e^(-375x/3960))^2 * ( 1 -e^(-264x/3960)) * e^(-264x/3960) * 264/3960 + (1 - e^(-375x/3960))^2 * (1 - e^(-264x/3960))^2 * (1 - e^(-165x/3960)) * e^(-165x/3960) * 165/3960) * e^(-2352x/3960) * 2 * x dx
Since this integral sums the individual probabilities of winning the fire bet at all times(x) and then multiplies by time (x), it gives us the weighed average of ~0.001201 decisions to win the fire bet. That is the average all of all outcomes, including the losing ones. We are only interested in outcomes where the fire bet was won, so take 0.001201 divided by 0.0001624 (the probability of winning) to get ~7.39 average total decisions (points won) when the winning the fire bet. The exact answer is:
51,194,997,861,765,388,097,526,966,955,556,874,130,535,332,020,426,690,698,014,074,625,318,137,025,571,849,255/
6,923,708,358,532,324,948,598,712,995,072,892,018,553,301,246,118,708,475,186,839,062,876,563,686,189,522,216
I will use the "direct method fire bet" integral in the example:
(
(1 - e^(-165x/3960))^2 * (1 - e^(-264x/3960))^2 * (1 - e^(-375x/3960)) * e^(-375x/3960) * 375/3960
+ (1 - e^(-165x/3960))^2 * ( 1 - e^(-375x/3960))^2 * ( 1 -e^(-264x/3960)) * e^(-264x/3960) * 264/3960
+ (1 - e^(-375x/3960))^2 * (1 - e^(-264x/3960))^2 * (1 - e^(-165x/3960)) * e^(-165x/3960) * 165/3960
) * e^(-2352x/3960) * 2 dx
Let y = e^(-x/3960): the integral becomes
2 *
(
(1 - y^165)^2 * (1 - y^264)^2 * (1 - y^375) * y^375 * 375/3960
+ (1 - y^165)^2 * (1 - y^375)^2 * (1 - y^264) * y^264 * 264/3960
+ (1 - y^375)^2 * (1 - y^264)^2 * (1 - y^165) * y^165 * 165/3960
)
* y^2352 dx
Expand all of the squares, and take 1/3960 out of the sum:
2 / 3960 *
(
(1 - 2 y^165 + y^330) * (1 - 2 y^264 + y^528) * (1 - y^375) * y^375 * 375
+ (1 - 2 y^165 + y^330) * (1 - 2 y^375 + y^750) * (1 - y^264) * y^264 * 264
+ (1 - 2 y^375 + y^750) * (1 - 2 y^264 + y^528) * (1 - y^165) * y^165 * 165
)
* y^2352 dx
I will not bore you with calculating the expansion (hint: use Excel, and a lot of cutting and pasting), but this is:
1 / 1980 *
(
165 y^2517
+ 264 y^2616
- 165 y^2682
+ 375 y^2727
- 528 y^2781 - 330 y^2781
- 264 y^2880
- 750 y^2892 - 330 y^2892
+ 264 y^2946 + 330 y^2946
- 750 y^2991 - 528 y^2991
+ 528 y^3045 + 165 y^3045
+ 375 y^3057 + 330 y^3057
- 375 y^3102
+ 1500 y^3156 + 1056 y^3156 + 660 y^3156
- 264 y^3210 - 165 y^3210
+ 375 y^3255 + 528 y^3255
+ 750 y^3267 + 165 y^3267
- 750 y^3321 - 528 y^3321 - 660 y^3321
+ 750 y^3366 + 264 y^3366
- 750 y^3420 - 1056 y^3420 - 330 y^3420
- 375 y^3432 - 165 y^3432
- 1500 y^3531 - 528 y^3531 - 330 y^3531
+ 375 y^3585 + 528 y^3585 + 330 y^3585
- 375 y^3630 - 264 y^3630
+ 750 y^3696 + 264 y^3696 + 330 y^3696
+ 750 y^3795 + 528 y^3795 + 165 y^3795
- 375 y^3960 - 264 y^3960 - 165 y^3960
)
"Now what?"
d/dx (e^(nx)) = e^(nx) / n
y^n = e^(x * (-n/3960)), so d/dx (y^n) = e^(x * (-n/3960)) * (-3960/n)
For positive n, at x = +INF, this is 0; at x = 0, this is -3960/n, so the integral over x = 0 to +INF = 3960/n
Replace each "a y^b" with "3960 * b / a"; you can take 3960 out of each numerator and multiply the 1/1980 term by 3960 to get 2.
The solution becomes
2 *
(
165 / 2517
+ 264 / 2616
- 165 / 2682
+ 375 / 2727
- 858 / 2781
- 264 / 2880
- 1080 / 2892
+ 594 / 2946
- 1278 / 2991
+ 693 / 3045
+ 705 / 3057
- 375 / 3102
+ 3216 / 3156
- 429 / 3210
+ 903 / 3255
+ 915 / 3267
- 1938 / 3321
+ 1014 / 3366
- 2136 / 3420
- 540 / 3432
- 2358 / 3531
+ 1233 / 3585
- 639 / 3630
+ 1344 / 3696
+ 1443 / 3795
- 804 / 3960
)
Easy, right?
The sum is done one term at a time (i.e. start with the first two, then add the third, then add the fourth, and so on), using:
a / b + c / d = (ad + bc) / bd
No, you can't do this in Excel, as you will soon run out of digits of precision.
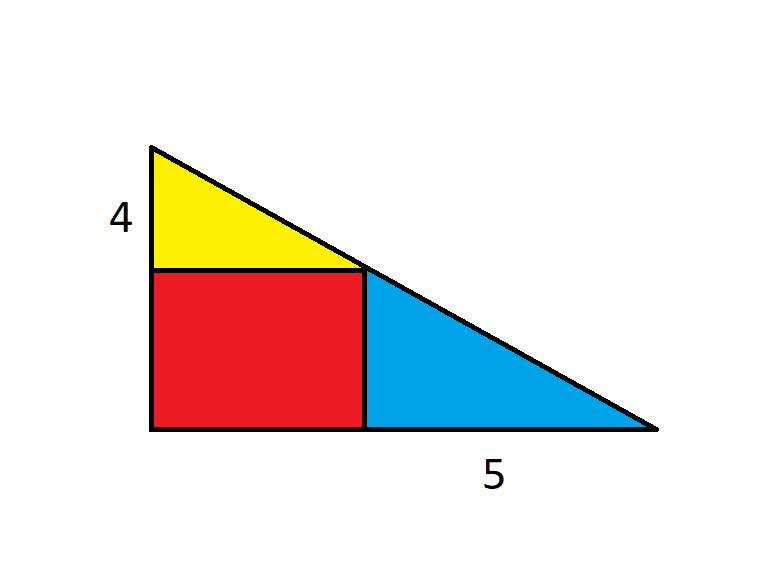
Questions:
1. What is the area of the red rectangle*?
2. What is the least possible area of the entire figure?
In case it's not clear, the height of the yellow triangle is 4 and the base of the blue triangle is 5.
* Corrected from square
Quote: WizardMy apologies if business is not concluded on Don's problem. Here is something easier.
Questions:
1. What is the area of the red square?
2. What is the least possible area of the entire figure?
In case it's not clear, the height of the yellow triangle is 4 and the base of the blue triangle is 5.
Clarify: the red portion is supposed to be a square, and not just a rectangle. The way it appears, it is not a square.
Or perhaps question 1 requires that it be a square, but question 2 requires only that it be a rectangle?
Also, my "problem" was not a problem, but an explanation as to how to calculate the exact rational number solution of a Poisson-based probability problem, rather than depending on, e.g., Integral Calculator to do it for you.
Quote: ThatDonGuyClarify: the red portion is supposed to be a square, and not just a rectangle.
Yes, I should have said red rectangle.
Let b be the "missing" length of a leg of the blue triangle, and y the "missing" length of a leg of the yellow one.
Both problems depend on the fact that the blue triangle, the yellow triangle, and the large triangle are all similar; 4 / y = b / 5 = (4 + b) / (5 + y).
For #1, y = b, so 4 / b = b / 5, which means b = 2 sqrt(5), and the area of the large triangle = 1/2 (4 + 2 sqrt(5)) (5 + 2 sqrt(5)) = 20 + 9 sqrt(5)
For #2, 4 / y = b / 5, so y = 20 / b. The area of the triangle is 1/2 (4 + b) (5 + y) = 1/2 (4 + b) (5 + 20/b) = 20 + 5/2 b + 40/b.
Let A denote the area; the first derivative with respect to b, dA / db = 5/2 - 40/b^2. This equals zero when b^2 = 16; since b > 0, b = 4.
Note that the second derivative, d^2A / db^2 = 80/b^3, which is positive when b = 4, so A is a minimum at b = 4.
b = 4, so y = 5, and the minimum area = 1/2 (4 + 4) (5 + 5) = 40.
Note that there is no maximum area, as 20 + 5/2 b + 40/b approaches infinity as b approaches infinity.
Quote: ThatDonGuyWell, the area of the red rectangle could be anything
I disagree. It has a specific answer.
If the area of the rectangle were a billion, you couldn't inscribe it a right triangle with the 4 and 5 distances given. If you feel otherwise, please give me the dimensions of a the rectangle with area one billion.
Quote: WizardI disagree. It has a specific answer.
If the area of the rectangle were a billion, you couldn't inscribe it a right triangle with the 4 and 5 distances given. If you feel otherwise, please give me the dimensions of a the rectangle with area one billion.
1) x= width of rectangle, y = height of rectangle, 4/x=y/5, xy = 20
2) Entire figure area, A = (4+y) * (5 +x)/2 = (20 + 4x + 5y + xy)/2, and xy = 20
So, A = 20 + 2x + 50/x
dA/dx = 2 - 50/x^2 = 0
x= 5
Minimum A = 20 + 2(5) + 50/5 = 40
What if x=0, y= 0 ? still applicable to your question ?
Quote: WizardI disagree. It has a specific answer.
If the area of the rectangle were a billion, you couldn't inscribe it a right triangle with the 4 and 5 distances given. If you feel otherwise, please give me the dimensions of a the rectangle with area one billion.
Oh, you're looking for the area of the rectangle. I misread it - I thought you were looking for the area of the large triangle.
In that case...
As stated in my earlier solution, if b is the length of the undetermined leg of the blue triangle and y the length of the undetermined length of the yellow triangle, then 4 / y = b / 5, so by = 20. Since the rectangle has height b and width y, its area is yb, or 20.
Quote: ssho88
1) x= width of rectangle, y = height of rectangle, 4/x=y/5, xy = 20
2) Entire figure area, A = (4+y) * (5 +x)/2 = (20 + 4x + 5y + xy)/2, and xy = 20
So, A = 20 + 2x + 50/x
dA/dx = 2 - 50/x^2 = 0
x= 5
Minimum A = 20 + 2(5) + 50/5 = 40
What if x=0, y= 0 ? still applicable to your question ?
I agree to both!
Quote: WizardI agree to both!
What if x=0, y= 0 ? still applicable to your question ?
Quote: ssho88What if x=0, y= 0 ? still applicable to your question ?
If you want to be pedantic, if x and y = 0, it's no longer a rectangle, but a point. Even if just one of them = 0, it's a line segment.
Itís very useful to see that some of these can be hashed out manually. However, if you need to take the integral of, for instance, 1-(1-(1+(x/6)+(x/6)^2/2+ (x/6)^3/6+ (x/6)^4/24+ (x/6)^5/120)*e^(-x/6))^6 or 1-(1-1/e^(x/38))^38, would it be feasible to do it manually ?Quote: ThatDonGuyWho wants a rather lengthy explanation of how to calculate the exact (rational number) solution to these integrals?
I will use the "direct method fire bet" integral in the example:
(
(1 - e^(-165x/3960))^2 * (1 - e^(-264x/3960))^2 * (1 - e^(-375x/3960)) * e^(-375x/3960) * 375/3960
+ (1 - e^(-165x/3960))^2 * ( 1 - e^(-375x/3960))^2 * ( 1 -e^(-264x/3960)) * e^(-264x/3960) * 264/3960
+ (1 - e^(-375x/3960))^2 * (1 - e^(-264x/3960))^2 * (1 - e^(-165x/3960)) * e^(-165x/3960) * 165/3960
) * e^(-2352x/3960) * 2 dx
Let y = e^(-x/3960): the integral becomes
2 *
(
(1 - y^165)^2 * (1 - y^264)^2 * (1 - y^375) * y^375 * 375/3960
+ (1 - y^165)^2 * (1 - y^375)^2 * (1 - y^264) * y^264 * 264/3960
+ (1 - y^375)^2 * (1 - y^264)^2 * (1 - y^165) * y^165 * 165/3960
)
* y^2352 dx
Expand all of the squares, and take 1/3960 out of the sum:
2 / 3960 *
(
(1 - 2 y^165 + y^330) * (1 - 2 y^264 + y^528) * (1 - y^375) * y^375 * 375
+ (1 - 2 y^165 + y^330) * (1 - 2 y^375 + y^750) * (1 - y^264) * y^264 * 264
+ (1 - 2 y^375 + y^750) * (1 - 2 y^264 + y^528) * (1 - y^165) * y^165 * 165
)
* y^2352 dx
I will not bore you with calculating the expansion (hint: use Excel, and a lot of cutting and pasting), but this is:
1 / 1980 *
(
165 y^2517
+ 264 y^2616
- 165 y^2682
+ 375 y^2727
- 528 y^2781 - 330 y^2781
- 264 y^2880
- 750 y^2892 - 330 y^2892
+ 264 y^2946 + 330 y^2946
- 750 y^2991 - 528 y^2991
+ 528 y^3045 + 165 y^3045
+ 375 y^3057 + 330 y^3057
- 375 y^3102
+ 1500 y^3156 + 1056 y^3156 + 660 y^3156
- 264 y^3210 - 165 y^3210
+ 375 y^3255 + 528 y^3255
+ 750 y^3267 + 165 y^3267
- 750 y^3321 - 528 y^3321 - 660 y^3321
+ 750 y^3366 + 264 y^3366
- 750 y^3420 - 1056 y^3420 - 330 y^3420
- 375 y^3432 - 165 y^3432
- 1500 y^3531 - 528 y^3531 - 330 y^3531
+ 375 y^3585 + 528 y^3585 + 330 y^3585
- 375 y^3630 - 264 y^3630
+ 750 y^3696 + 264 y^3696 + 330 y^3696
+ 750 y^3795 + 528 y^3795 + 165 y^3795
- 375 y^3960 - 264 y^3960 - 165 y^3960
)
"Now what?"
d/dx (e^(nx)) = e^(nx) / n
y^n = e^(x * (-n/3960)), so d/dx (y^n) = e^(x * (-n/3960)) * (-3960/n)
For positive n, at x = +INF, this is 0; at x = 0, this is -3960/n, so the integral over x = 0 to +INF = 3960/n
Replace each "a y^b" with "3960 * b / a"; you can take 3960 out of each numerator and multiply the 1/1980 term by 3960 to get 2.
The solution becomes
2 *
(
165 / 2517
+ 264 / 2616
- 165 / 2682
+ 375 / 2727
- 858 / 2781
- 264 / 2880
- 1080 / 2892
+ 594 / 2946
- 1278 / 2991
+ 693 / 3045
+ 705 / 3057
- 375 / 3102
+ 3216 / 3156
- 429 / 3210
+ 903 / 3255
+ 915 / 3267
- 1938 / 3321
+ 1014 / 3366
- 2136 / 3420
- 540 / 3432
- 2358 / 3531
+ 1233 / 3585
- 639 / 3630
+ 1344 / 3696
+ 1443 / 3795
- 804 / 3960
)
Easy, right?
The sum is done one term at a time (i.e. start with the first two, then add the third, then add the fourth, and so on), using:
a / b + c / d = (ad + bc) / bd
No, you can't do this in Excel, as you will soon run out of digits of precision.
Incidentally, the result is the expected number of rolls to hit all six sides of a single die at least six times and the expected number of spins to hit all 38 numbers on a roulette wheel at least once, respectively
Quote: ssho88What if x=0, y= 0 ? still applicable to your question ?
No, because it wouldn't be inscribed in the triangle.
Quote: Ace2Itís very useful to see that some of these can be hashed out manually. However, if you need to take the integral of, for instance, 1-(1-(1+(x/6)+(x/6)^2/2+ (x/6)^3/6+ (x/6)^4/24+ (x/6)^5/120)*e^(-x/6))^6 or 1-(1-1/e^(x/38))^38, would it be feasible to do it manually ?
Who said anything about "feasible"? Just integrating something like x e^(-x/6) is a pain.
Integrate by parts:
u = x; dv = e^(-x/6) dx
du = dx; v = -6 e^(-x/6)
The integral = -6x e^(-x/6) - the integral of -6 e^(-x/6) dx = -6x e^(-x/6) + 6 (-6 e^(x/6)) = -(6x + 36) e^(-x/6) = -6 (x + 6) / e^(x/6)
As x approaches positive infinity, the numerator and denominator approach positive infinity, so apply L'Hopital's Rule; the limit of 1 / (6 e^(x/6)) = 0, so the definite integral over x from 0 to positive infinity = 0 - (-6 (0 + 6) / e^0)) = 36.
1 + 2 + 3 + ... + N = (N+1) + (N+2) + ... (N+K)?
I have solutions so far for N = 2, 14, 84, 492, 2870, 16730 and 97512.
And now I just ruined it for myself by looking up the sequence on OEIS.org :) Well, it was fun anyway for a few minutes.Quote: teliotWhat is the largest solution you can find of the equation:
1 + 2 + 3 + ... + N = (N+1) + (N+2) + ... (N+K)?
I have solutions so far for N = 2, 14, 84, 492, 2870, 16730 and 97512.
I didn't see the solution beforehand...Quote: Wizard...I agree to both!
The second idea is then to flip the 5-wide triangle to lie on top of the diagonal line. Construct a rectangle 4x5 (to the right of the 4-side). Where x is less than 5, the top triangle extends below this rectangle. Hence the total area of the original triangle exceeds 40. Similar logic applies where x exceeds 5 except the 4-side triangle extends beyond the rectangle. Hence 40 is the minimum.


For full credit, I'd like to the degree of efficiency (meaning ratio of the volume of cannonballs to to the volume of the whole pyramid), both ways, as the number of cannonballs approaches infinity?
There will probably be an extra credit problem coming up, but one thing at a time.
Quote: ThatDonGuyFor efficiency calculation purposes, how is the "volume of the whole pyramid" measured - the volume of the circumscribing pyramid (I just had a 40-year-old flashback to an AMC exam problem I had in high school), or the volume of the pyramid whose vertices are the centers of the golf balls at each vertex?
As the number of cannonballs approaches infinity, it shouldn't matter how exactly the volume is of the pyramid is measured.
However, if you must have an answer, let's keep it simple and say the length of a side of the base is the sum of the diameters of the cannonballs in a that side. For the height and slant height, use the same logic, keeping the angles in the pyramid correct.
Quote: WizardAs the number of cannonballs approaches infinity, it shouldn't matter how exactly the volume is of the pyramid is measured.
However, if you must have an answer, let's keep it simple and say the length of a side of the base is the sum of the diameters of the cannonballs in a that side. For the height and slant height, use the same logic, keeping the angles in the pyramid correct.
r = radius of golf ball.
For square base, imagine a ball put on top of 4 balls and you join the center of five balls to form a square base pyramid, the vertical height of square base pyramid = 2^0.5 * r = 1.414r, and the slant distance = 2r.
For triangular base, imagine a ball put on top of 3 balls and you join the center of four balls to form a triangular base pyramid, the vertical height of triangular base pyramid = 2/3 * 6^0.5 * r = 1.633r, and the slant distance = 2r.
From there, we can calculate the total vertical height of N layers of balls, Am I missing something ?
Assume the "volume of the shape" is the volume of the tetrahedron/pyramid whose vertices are the centers of the cannonballs at the vertices.
Also assume each cannonball has radius 1.
If there are N levels:
The number of cannonballs in the tetrahedron is N (N^2 + 3 N + 2) / 6
The combined volume of the cannonballs is N (N^2 + 3 N + 2) / 6 * 4 PI / 3
= 2 PI (N^3 + 3 N^2 + 2 N) / 9
The tetrahedron is a regular tetrahedron of side length 2 (N - 1)
The volume is (2 (N - 1))^3 / (6 sqrt(2))
= 2 sqrt(2) / 3 * (N^3 - 3 N^2 + 3 N - 1)
The number of cannonballs in the pyramid is N (2 N^2 + 3 N + 1) / 6
The combined volume of the cannonballs is N (2 N^2 + 3 N + 1) / 6 * 4 PI / 3
= 2 PI (2 N^3 + 3 N^2 + N) / 9
The pyramid has sides of length 2 (N - 1)
The area of the base is 4 (N - 1)^2, and the height is (N - 1) sqrt(2),
The volume is 4 (N - 1)^2 * (N - 1) sqrt(2) / 3
= 4 sqrt(2) * (N^3 - 3 N^2 + 3 N - 1) / 3
The tetrahedron's efficiency is
(2 PI (N^3 + 3 N^2 + 2 N) / 9) / (2 sqrt(2) * (N^3 - 3 N^2 + 3 N - 1) / 3)
= PI / (3 sqrt(2)) * (N^3 + 3 N^2 + 2 N) / (N^3 - 3 N^2 + 3 N - 1)
As N approaches infinity, this approaches PI * sqrt(2) / 6
The pyramid's efficiency is
(2 PI (2 N^3 + 3 N^2 + N) / 9) / (4 sqrt(2) * (N^3 - 3 N^2 + 3 N - 1) / 3)
= PI / (3 sqrt(2)) * (N^3 + 3/2 N^2 + 1/2 N) / (N^3 - 3 N^2 + 3 N - 1)
As N approaches infinity, this also approaches PI * sqrt(2) / 6
The two have equal efficiency - specifically, PI sqrt(2) / 6
Quote: WizardWhich method of stacking cannonballs is the most efficient -- a pyramid with a square base or triangular?
For full credit, I'd like to the degree of efficiency (meaning ratio of the volume of cannonballs to to the volume of the whole pyramid), both ways, as the number of cannonballs approaches infinity?
There will probably be an extra credit problem coming up, but one thing at a time.
Good problem. One of my calc professors in college solved the Kepler conjecture (ie, whatís the most efficient way to pack spheres). When I was in his class was before he solved it, but he was obsessed with it. Talked about it during multiple classes. He had reduced the problem to a differential equation but was unable to integrate it. A few years later he managed to find the integral and solved it.
Quote: ThatDonGuy
Assume the "volume of the shape" is the volume of the tetrahedron/pyramid whose vertices are the centers of the cannonballs at the vertices.
Also assume each cannonball has radius 1.
If there are N levels:
The number of cannonballs in the tetrahedron is N (N^2 + 3 N + 2) / 6
The combined volume of the cannonballs is N (N^2 + 3 N + 2) / 6 * 4 PI / 3
= 2 PI (N^3 + 3 N^2 + 2 N) / 9
The tetrahedron is a regular tetrahedron of side length 2 (N - 1)
The volume is (2 (N - 1))^3 / (6 sqrt(2))
= 2 sqrt(2) / 3 * (N^3 - 3 N^2 + 3 N - 1)
The number of cannonballs in the pyramid is N (2 N^2 + 3 N + 1) / 6
The combined volume of the cannonballs is N (2 N^2 + 3 N + 1) / 6 * 4 PI / 3
= 2 PI (2 N^3 + 3 N^2 + N) / 9
The pyramid has sides of length 2 (N - 1)
The area of the base is 4 (N - 1)^2, and the height is (N - 1) sqrt(2),
The volume is 4 (N - 1)^2 * (N - 1) sqrt(2) / 3
= 4 sqrt(2) * (N^3 - 3 N^2 + 3 N - 1) / 3
The tetrahedron's efficiency is
(2 PI (N^3 + 3 N^2 + 2 N) / 9) / (2 sqrt(2) * (N^3 - 3 N^2 + 3 N - 1) / 3)
= PI / (3 sqrt(2)) * (N^3 + 3 N^2 + 2 N) / (N^3 - 3 N^2 + 3 N - 1)
As N approaches infinity, this approaches PI * sqrt(2) / 6
The pyramid's efficiency is
(2 PI (2 N^3 + 3 N^2 + N) / 9) / (4 sqrt(2) * (N^3 - 3 N^2 + 3 N - 1) / 3)
= PI / (3 sqrt(2)) * (N^3 + 3/2 N^2 + 1/2 N) / (N^3 - 3 N^2 + 3 N - 1)
As N approaches infinity, this also approaches PI * sqrt(2) / 6
The two have equal efficiency - specifically, PI sqrt(2) / 6
I agree!
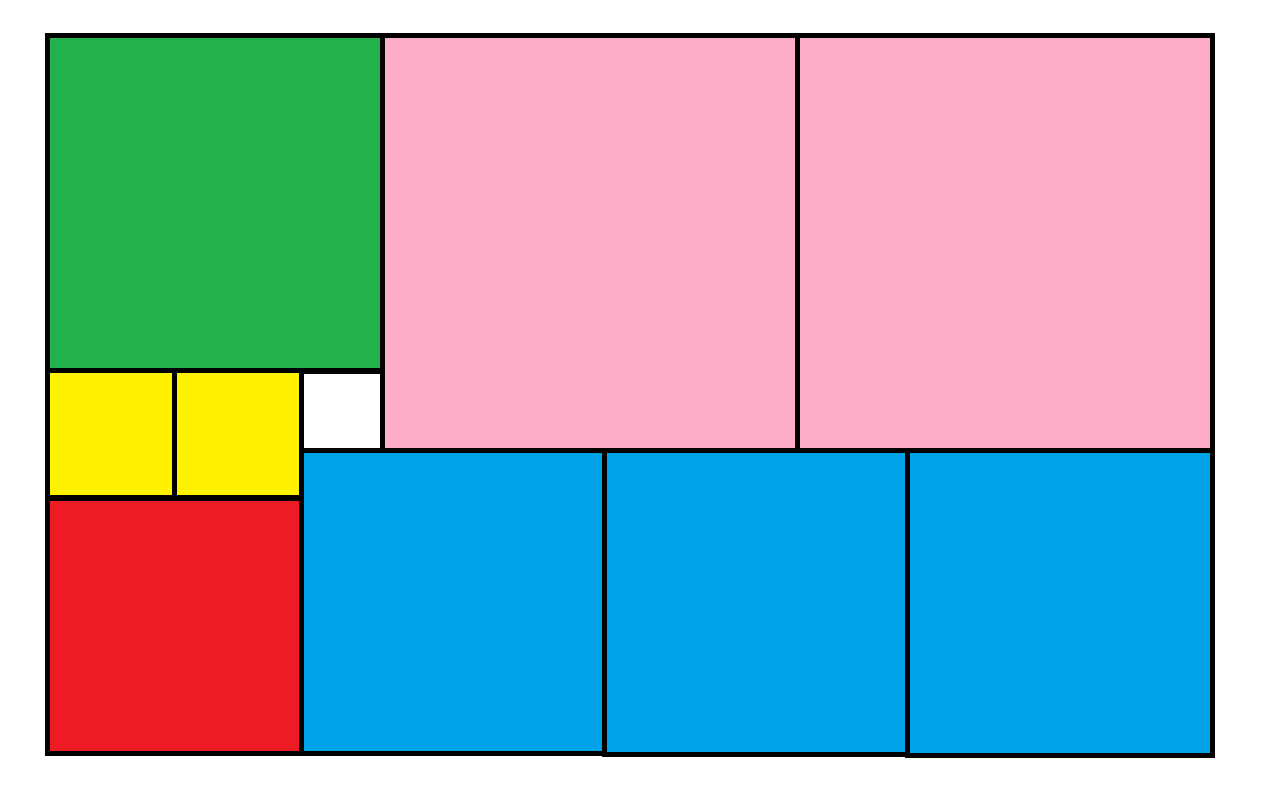
The above figure contains 10 squares inscribed in a rectangle. The white square has side length of 1. What is the area of the entire rectangle?
Please, no cheating with rulers.
Simultaneous equations gets it...Quote: Wizard...The above figure contains 10 squares inscribed in a rectangle. The white square has side length of 1. What is the area of the entire rectangle?...
Green = 2x+1
Pink = 2x+2
Red = 2x
Blue = 3x-1
Then look at the widths 2 Pink + Green (6x+5) or 3 Blue + Red (11x-3) giving x=8/5
So width = 14 3/5 and Height = (Pink+Blue) 5x+1 = 9
So area = 131.4.
Quote: charliepatrickSimultaneous equations gets it...
Let Yellow = x
Green = 2x+1
Pink = 2x+2
Red = 2x
Blue = 3x-1
Then look at the widths 2 Pink + Green (6x+5) or 3 Blue + Red (11x-3) giving x=8/5
So width = 14 3/5 and Height = (Pink+Blue) 5x+1 = 9
So area = 131.4.
I agree!
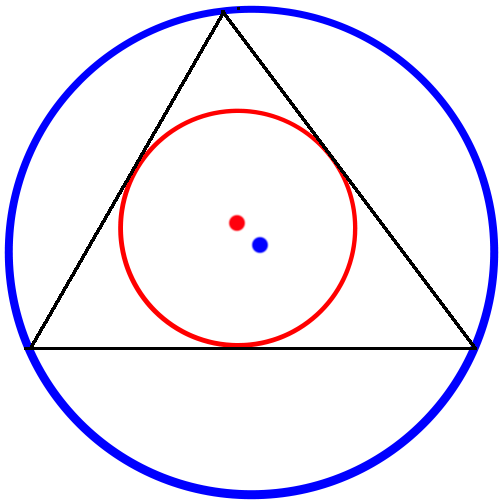
Triangle ABC has side lengths of 13, 14, and 15.
X is the center of the inscribed circle - that is, the circle that is tangent to all three sides. (In the image, it is in red.)
Y is the center of the circumscribed circle - that is, the circle that goes through A, B, and C. (In the image, it is in blue.)
What is the distance from X to Y?
If you want to make it easier, here are three hints:
The radius of the inscribed circle is 4
The radius of the circumscribed circle is 65/8
If AB has length 13 and BC has length 15, the distance from B to the point where the inscribed circle touches BC is 7.


