Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
Good one. I guess this joke would only work in written form.Quote: WizardThere are only 10 kinds of people -- Those who get binary arithmetic and those who don't.
Quote: charliepatrickIt's all about the base!
Quote: DogHandWith thanks to Charlie for the hint, I get...
220 = 24 in base 3. Each number is 24 in based decreasing from 12 to 2.
Dog Hand
Correct!!
----------------------------------------




A 10kg box is placed on the back of a lorry. As the lorry accelerates uniformly from 0 to 36 kmh^-1 in 5 seconds, the box begins to slide. The lorry then continues to drive at a constant speed and the box comes to rest.
If the box slides 2 meters in total, and assuming g=9.8 ms^-2, find µ, the coefficient of friction between the box and the surface.
[For simplicity, assume throughout that the coefficient of friction remains constant and that the dynamic friction (once the box begins sliding) is the same as the static (limiting) friction.]
Quote: GialmereIt's toughie Tuesday. Let's go for a drive...
A 10kg box is placed on the back of a lorry. As the lorry accelerates uniformly from 0 to 36 kmh^-1 in 5 seconds, the box begins to slide. The lorry then continues to drive at a constant speed and the box comes to rest.
If the box slides 2 meters in total, and assuming g=9.8 ms^-2, find µ, the coefficient of friction between the box and the surface.
[For simplicity, assume throughout that the coefficient of friction remains constant and that the dynamic friction (once the box begins sliding) is the same as the static (limiting) friction.]
I used high school physics and found 0.1877551.
Quote: GialmereAs the lorry accelerates uniformly from 0 to 36 kmh^-1 in 5 seconds,
What does kmh^-1 mean?
Do you mean the rate of acceleration is constant, the lorry starts from a standing position and reaches 35 kilometers per hour in five seconds?
Also, what is a lorry?
Quote: WizardWhat does kmh^-1 mean?
Do you mean the rate of acceleration is constant, the lorry starts from a standing position and reaches 35 kilometers per hour in five seconds?
Also, what is a lorry?
Yes, and British for "truck".
Quote: GialmereYes, and British for "truck".
I havenít got a correct confirmation, so I recalculated it. My new result is mu=0.18896447.
Quote: Ace2In Crapless Craps, what is the chance of winning the Fire Bet with all ten points?
spreadsheet
I saw there was an old thread on this. I'm looking for a calculated (not simulated) answer expressed as a rational numberQuote: miplet
I disagree with your answer
I get 1 in 344,842,585.
I'll show my method if I'm correct.
Quote: Ace2I'm looking for a calculated (not simulated) answer expressed as a rational number
I get:
125,085,337,830,737
,750,040,946,884,515,600,828,826,106,122,701,544,847,430,450
,629,046,605,089,708,493,923,039,495,721,017,570,418,222,323
,016,473,845,293,309,175,319,694,738,875,002,802,771,338,500
,366,299,331,953,447,220,689,670,202,784,565,639,415,289,332
,084,779,481,597,229,081,746,080,364,803,215,921,066,911,536
,541,381,291,811,341,713,825,167,788,888,871,197,475,636,470
,784,515,810,574,611,990,369,837,114,575,201,669,878,148,297
/
43,134,751,192,953,914,210,993
,943,271,802,543,777,980,988,349,922,891,546,230,519,480,217
,557,626,817,255,231,365,456,478,947,627,840,676,555,835,923
,392,957,024,113,969,618,568,826,138,354,283,301,839,972,359
,049,974,938,603,820,014,108,197,177,751,482,827,734,201,244
,571,353,546,913,323,627,624,872,502,898,073,424,297,340,815
,406,874,056,759,075,587,522,737,125,509,897,688,175,170,811
,478,174,333,289,594,416,341,915,851,631,174,536,884,518,568
(which is about 1 / 344,842,584.6)
Quote: WizardLet the record show I beat Don by 13 seconds.
But you didn't express it as a rational number, as requested
Quote: ThatDonGuyBut you didn't express it as a rational number, as requested
Grrrrrrrrrrrrrrrr!
Today I have to declare ThatDonGuy as winner since he was the first to provide the answer in rational format as requested. What a close race
I would be interested in seeing everyone's method...I'm guessing the Wizard integrated a Poisson formula like I did.
Quote: Ace2I would be interested in seeing everyone's method...I'm guessing the Wizard integrated a Poisson formula like I did.
As usual, I used a brute force Markov chain.
Let a2, a3, ..., a12 = 0 if that point has not been made yet, and 1 if it has.
Let P(a2, a3, ..., a12) be the probability of winning from that state; P(1,1,1,1,1,1,1,1,1,1) = 1.
P(a2, a3, ..., a12) = 1/30 x 1/7 x P(1, a3, a4, ..., a12) + 1/15 x 1/4 x P(a2, 1, a4, ..., a12) + 1/10 x 1/3 x P(a2, a3, 1, a5, ..., a12) + ... + 1/30 x 1/7 x P(a2, a3, ..., a11, 1)
The two fractions are the probability that this is the point (1/30 for 2 and 12, 2/30 = 1/15 for 3 and 11, 3/30 = 1/10 for 4 and 10, 4/30 = 2/15 for 5 and 9, and 5/30 = 1/6 for 6 and 8) and the probability that, if it is the point, the point is made (1/7 for 2 and 12, 2/8 = 1/4 for 3 and 11, 3/9 = 1/3 for 4 and 10, 4/10 = 2/5 for 5 and 9, and 5/11 for 6 and 8)
Work backwards from (1,1,1,...,1,1,0) to (0,0,0,...,0,0,0), which is the solution.
Quote: Ace2I would be interested in seeing everyone's method...I'm guessing the Wizard integrated a Poisson formula like I did.
Yes, of course. You taught me and won't let me forget the method.
Here is the integral in text form: exp(-7303x/13860)*(1-exp(-x/252))^2*(1-exp(-x/72))^2*(1-exp(-x/36))^2*(1-exp(-2x/45))^2*(1-exp(-25x/396))^2*(7303/13860)
Here it is in proper notation:
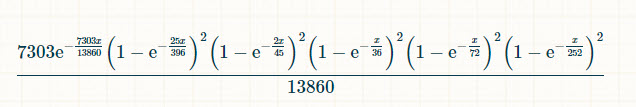
Here is the screen with the answer. One has to scroll way over to the right to see all the digits.
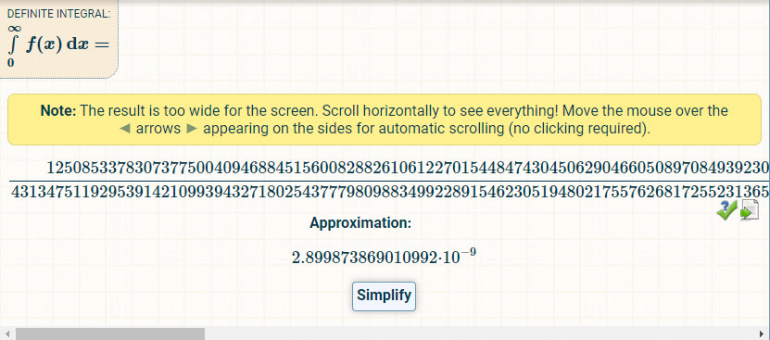
I hope this proves I at least had the right answer and just didn't report it properly.
3^2 + 4^2 = 5^2.
10^2 + 11^2 + 12^2 = 13^2 + 14^2
21^2 + 22^2 + 23^2 + 24^2 = 25^2 + 26^2 + 27^2
18^2 + 19^2 + 20^2 + ... + 34^2 = 35^2 + 36^2 + 37^2 + ... + 42^2
What's the longest one you can find?
Quote: acesideI havenít got a correct confirmation, so I recalculated it. My new result is mu=0.18896447.
Correct!!
Very good.
---------------------------------------
Did you hear about the Star Wars fan who ate a truck?
They call him the The Mandalorryin.
I owe all three of you a beer:
Miplet: First to solve
ThatDonGuy: First to post a rational answer
Wizard: In my opinion, he provided the most elegant/efficient solution...expressed as a single line formula
Incidentally, my method uses the same concept as the Wizard's but it's not exactly the same. I took 1 minus the integral over all time of:
(1-((1-1/e^(t/210))*(1-1/e^(t/60))*(1-1/e^(t/30))*(1-1/e^(4t/75))*(1-1/e^(5t/66)))^2)*1/e^(7303t/11550)*7303/11550 dt
Quote: teliotOkay ... new puzzle. A sum of consecutive squares equaling a sum of the following successive consecutive squares.
3^2 + 4^2 = 5^2.
10^2 + 11^2 + 12^2 = 13^2 + 14^2
21^2 + 22^2 + 23^2 + 24^2 = 25^2 + 26^2 + 27^2
18^2 + 19^2 + 20^2 + ... + 34^2 = 35^2 + 36^2 + 37^2 + ... + 42^2
What's the longest one you can find?
Let there be A numbers on the left, and B on the right
(N - (A - 1))^2 + (N - (A - 2))^2 + ... + (N - 1)^2 + N^2 = (N + 1)^2 + (N + 2)^2 + ... + (N + B)^2
The left is the sum of 1^2 through N^2 - the sum of 1^2 through (N - A)^2
The right is the sum of 1^2 through (N + B)^2 - the sum of 1^2 through N^2
1^2 + 2^2 + ... + N^2 = N (N + 1) (2N + 1) / 6 for all positive integers N
1/6 N (N + 1) (2N + 1) - 1/6 (N - A) (N - A + 1) (2 (N - A) + 1) = 1/6 (N + B) (N + B + 1) (2 (N + B) + 1) - 1/6 N (N + 1) (2N + 1)
N (N + 1) (2N + 1) - (N - A) (N - A + 1) (2 (N - A) + 1) = (N + B) (N + B + 1) (2 (N + B) + 1) - N (N + 1) (2N + 1)
The largest sum I have found so far has 6195 terms:
385^2 + 386^2 + ... + 5222^2 = 5223^2 + 5224^2 + ... + 6579^2 = 47,461,421,035
Quote: Ace2Incidentally, my method uses the same concept as the Wizard's but it's not exactly the same. I took 1 minus the integral over all time of:
(1-((1-1/e^(t/210))*(1-1/e^(t/60))*(1-1/e^(t/30))*(1-1/e^(4t/75))*(1-1/e^(5t/66)))^2)*1/e^(7303t/11550)*7303/11550 dt
I understand the first five terms, but where does 7303 / 11550 come from?
It's the probability of sevening out. Sum the first five terms, multiply by 2, then add 7303/11550 and it equals 1.Quote: ThatDonGuyI understand the first five terms, but where does 7303 / 11550 come from?
The formula says: while at least one point has not been won and no there have been no seven-outs, what's the chance that the next decision is a seven out?
Clever! And beats my largest by (ehem) a few terms.Quote: ThatDonGuy
Let there be A numbers on the left, and B on the right
(N - (A - 1))^2 + (N - (A - 2))^2 + ... + (N - 1)^2 + N^2 = (N + 1)^2 + (N + 2)^2 + ... + (N + B)^2
The left is the sum of 1^2 through N^2 - the sum of 1^2 through (N - A)^2
The right is the sum of 1^2 through (N + B)^2 - the sum of 1^2 through N^2
1^2 + 2^2 + ... + N^2 = N (N + 1) (2N + 1) / 6 for all positive integers N
1/6 N (N + 1) (2N + 1) - 1/6 (N - A) (N - A + 1) (2 (N - A) + 1) = 1/6 (N + B) (N + B + 1) (2 (N + B) + 1) - 1/6 N (N + 1) (2N + 1)
N (N + 1) (2N + 1) - (N - A) (N - A + 1) (2 (N - A) + 1) = (N + B) (N + B + 1) (2 (N + B) + 1) - N (N + 1) (2N + 1)
The largest sum I have found so far has 6195 terms:
385^2 + 386^2 + ... + 5222^2 = 5223^2 + 5224^2 + ... + 6579^2 = 47,461,421,035
Quote: teliotClever! And beats my largest by (ehem) a few terms.Quote: ThatDonGuy
The largest sum I have found so far has 6195 terms:
385^2 + 386^2 + ... + 5222^2 = 5223^2 + 5224^2 + ... + 6579^2 = 47,461,421,035
8964 terms: 2931^2 + ... + 9487^2 = 9488^2 + ... + 11,894^2 = 276,276,145,995
Quote: Ace2I owe all three of you a beer:
Very gracious of you! I proudly accept.
Quote: ThatDonGuy
Let there be A numbers on the left, and B on the right
(N - (A - 1))^2 + (N - (A - 2))^2 + ... + (N - 1)^2 + N^2 = (N + 1)^2 + (N + 2)^2 + ... + (N + B)^2
The left is the sum of 1^2 through N^2 - the sum of 1^2 through (N - A)^2
The right is the sum of 1^2 through (N + B)^2 - the sum of 1^2 through N^2
1^2 + 2^2 + ... + N^2 = N (N + 1) (2N + 1) / 6 for all positive integers N
1/6 N (N + 1) (2N + 1) - 1/6 (N - A) (N - A + 1) (2 (N - A) + 1) = 1/6 (N + B) (N + B + 1) (2 (N + B) + 1) - 1/6 N (N + 1) (2N + 1)
N (N + 1) (2N + 1) - (N - A) (N - A + 1) (2 (N - A) + 1) = (N + B) (N + B + 1) (2 (N + B) + 1) - N (N + 1) (2N + 1)
The largest sum I have found so far has 6195 terms:
385^2 + 386^2 + ... + 5222^2 = 5223^2 + 5224^2 + ... + 6579^2 = 47,461,421,035
Can you also find some successive consecutive cubes for fun? Just replace all of the second power to the third power.
Quote: acesideCan you also find some successive consecutive cubes for fun? Just replace all of the second power to the third power.
I'll see what I can do.
Cubes should be easier, as 1^3 + 2^3 + ... + n^3 = (1 + 2 + ... + n)^2
which means if you start with
(n-(a-1))^3 + (n-(a-2))^3 + ... + n^3 = (n+1)^3 + (n+2)^3 + ... + (n+b)^3
you get:
(n (n + 1) / 2)^2 - ((n - a) (n - a + 1) / 2)^2 = ((n + b)(n + b + 1) / 2)^2 = (n (n + 1) / 2)^2
2 (n (n + 1))^2 = ((n + b) (n + b + 1))^2 + ((n-a) (n - a + 1))^2
So far, the only one I have found is 3^3 + 4^3 + 5^3 = 6^3 = 216
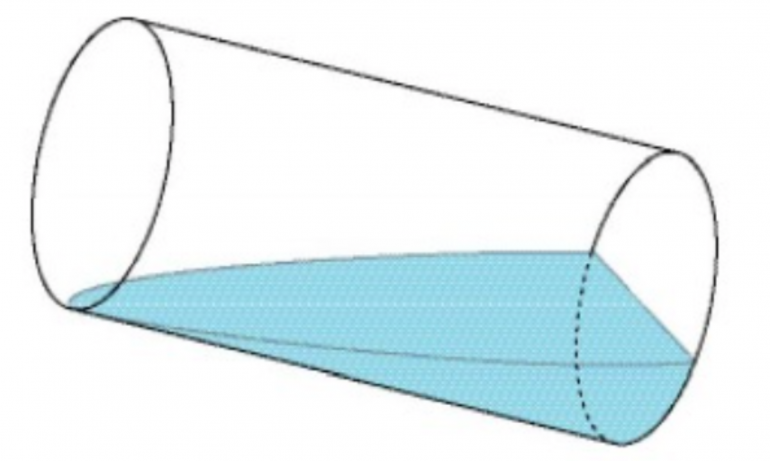
Fill a cylindrical glass with water. A quick way to empty it to exactly half its volume is to pour out the water until the water line just touches the circular bottom of the glass. Suppose you tip the glass further, until the water line crosses the center of the bottom of the glass (forming a diameter of the bottom circle).
What fraction of the glass' volume is now filled with water?
Within the range of the INT data size that's the only one I found as well.Quote: ThatDonGuyI'll see what I can do.
Cubes should be easier, as 1^3 + 2^3 + ... + n^3 = (1 + 2 + ... + n)^2
which means if you start with
(n-(a-1))^3 + (n-(a-2))^3 + ... + n^3 = (n+1)^3 + (n+2)^3 + ... + (n+b)^3
you get:
(n (n + 1) / 2)^2 - ((n - a) (n - a + 1) / 2)^2 = ((n + b)(n + b + 1) / 2)^2 = (n (n + 1) / 2)^2
2 (n (n + 1))^2 = ((n + b) (n + b + 1))^2 + ((n-a) (n - a + 1))^2
So far, the only one I have found is 3^3 + 4^3 + 5^3 = 6^3 = 216
Quote: Ace2Incidentally, my method uses the same concept as the Wizard's but it's not exactly the same. I took 1 minus the integral over all time of:
(1-((1-1/e^(t/210))*(1-1/e^(t/60))*(1-1/e^(t/30))*(1-1/e^(4t/75))*(1-1/e^(5t/66)))^2)*1/e^(7303t/11550)*7303/11550 dt
Let me see if I have this straight:
1 - 1/e^(t/210) is the probability that at least one point of 2 will be rolled and then made in time t (probability = 1/30 that a 2 will be rolled (ignoring 7s on the comeout) x 1/7 that a 2 will be rolled again before a 7 = 1/210)
1 - 1/e^(t/60) is the probability that at least one point of 3 will be rolled and then made in time t
1 - 1/e^(t/30) is the probability that at least one point of 4 will be rolled and then made in time t
...
1 - 1/e^(t/60) is the probability that at least one point of 11 will be rolled and then made in time t
1 - 1/e^(t/210) is the probability that at least one point of 12 will be rolled and then made in time t
The product is the probabiity that all 10 points will be rolled and then made in time t, so 1 - the product is the probability that at least one point will not be rolled and then made
1/e^(t*7303/11550) is the probability that a point will be rolled and then missed (i.e. a seven-out), so multiply this by the previous product to get the probability of sevening out before making all ten points
But why do you then multiply by 7303/11550 (the probability of sevening out in a particular pass)?
Quote: teliotWithin the range of the INT data size that's the only one I found as well.
I got as far as N = 13,000 (N is the largest term on the left side), and also could not find any others.
Quote: Gialmere
Fill a cylindrical glass with water. A quick way to empty it to exactly half its volume is to pour out the water until the water line just touches the circular bottom of the glass. Suppose you tip the glass further, until the water line crosses the center of the bottom of the glass (forming a diameter of the bottom circle).
What fraction of the glass' volume is now filled with water?
Let the height and radius of the glass equal 1. Then:
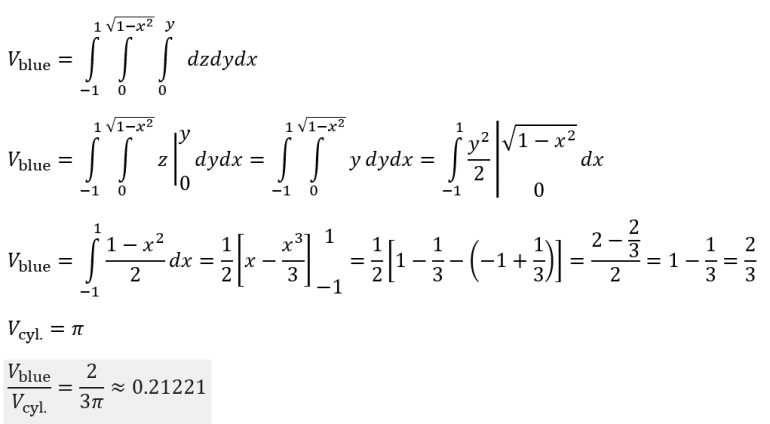
You have it mostly correct. Ignoring 7s on come out rolls, there are 11 possibilities: 1/210 winning a 2, 1/210 of winning a 12, 1/60 if winning a 3...etc and a 7303/11550 chance of sevening-out. As mentioned, these probabilities add up to 1.Quote: ThatDonGuyLet me see if I have this straight:
1 - 1/e^(t/210) is the probability that at least one point of 2 will be rolled and then made in time t (probability = 1/30 that a 2 will be rolled (ignoring 7s on the comeout) x 1/7 that a 2 will be rolled again before a 7 = 1/210)
1 - 1/e^(t/60) is the probability that at least one point of 3 will be rolled and then made in time t
1 - 1/e^(t/30) is the probability that at least one point of 4 will be rolled and then made in time t
...
1 - 1/e^(t/60) is the probability that at least one point of 11 will be rolled and then made in time t
1 - 1/e^(t/210) is the probability that at least one point of 12 will be rolled and then made in time t
The product is the probabiity that all 10 points will be rolled and then made in time t, so 1 - the product is the probability that at least one point will not be rolled and then made
1/e^(t*7303/11550) is the probability that a point will be rolled and then missed (i.e. a seven-out), so multiply this by the previous product to get the probability of sevening out before making all ten points
But why do you then multiply by 7303/11550 (the probability of sevening out in a particular pass)?
The second to last term of 1/e^(7303t/11550) is the probability that zero seven-outs have happened. And, as you know, the previous terms represent the probability that at least 1 of the 10 points has not been won. Therefore, starting from this state, if the next decision is a seven-out then the fire bet loses at that point in time t. There is a 7303/11550 chance of that happening so we multiply by that factor. Combining all that and integrating gives the sum of the probabilities, at all times from zero to infinity, that the fire bet will lose at that point in time.
Quote: Ace2You have it mostly correct. Ignoring 7s on come out rolls, there are 11 possibilities: 1/210 winning a 2, 1/210 of winning a 12, 1/60 if winning a 3...etc and a 7303/11550 chance of sevening-out. As mentioned, these probabilities add up to 1.
The second to last term of 1/e^(7303t/11550) is the probability that zero seven-outs have happened. And, as you know, the previous terms represent the probability that at least 1 of the 10 points has not been won. Therefore, starting from this state, if the next decision is a seven-out then the fire bet loses at that point in time t. There is a 7303/11550 chance of that happening so we multiply by that factor. Combining all that and integrating gives the sum of the probabilities, at all times from zero to infinity, that the fire bet will lose at that point in time.
So the last part of my explanation should be:
1/e^(t*7303/11550) is the probability that a point will not be rolled and then missed (i.e. a seven-out), so multiply this by the previous product to get the probability of not rolling and making every point nor missing any points (i.e. the bet is "still active").
Multiply this by 7303/11550 to get the probability of sevening out before making all ten points.
Subtract this result from 1 to get the probability of making all ten points before sevening out (i.e. winning the fire bet).
Quote: ChesterDog
Let the height and radius of the glass equal 1. Then:
Correct!!
lol! Apologies for the size of that picture. I was trying to whip out a puzzle on my cell at work. Heh, it looks just fine on a phone screen.
--------------------------------------------------------------
An optimist sees the glass as half full.
A pessimist sees the glass as half empty.
An engineer sees the glass as a waste of space and money since it's twice as big as you need.

1) Oh no! You want to play a board game but the box is missing its pair of standard dice. You look around and see some 3x5 cards. Hmm. Woo hoo! You can make two piles of six cards, each numbered 1-6, and Bam! By randomly drawing one card from each pile you have a "pair of dice".
D'oh! There's only eight cards. Hmm. A ha! You can still divide the cards into two sets (piles) and number them in such a way that by drawing two cards from each pile, and adding the four cards together, you get an integer from 2 to 12 with the same frequency of occurrence as rolling that sum on two standard dice.
How do you do it?
2) But wait! You recount and find there are actually nine cards available. Hmm. It occurs to you that you could number the nine cards in such a way that randomly drawing two cards from the pile of nine cards also gives an integer from 2 to 12 with the same frequency of occurrence as rolling that sum on two standard dice.
How do you do it?

The way to show it is to consider the binary for the numbers 1 thru 6 as 001 010 011 100 101 and 110, some which use two digits and others which use one. So picking two from 1 2 4 covers the two digit ones while 0+ another cover the others. Thus each set create the numbers 1 thru 6, so are equivalent to a regular die.
I think this is a trick question. I suspect it is impossible if you stick with the constraints of using integers and adding the two cards.
I've tried using negative numbers and adding, but can't find a solution.
I've tried multiplying, instead of adding, but still can't find a solution.
I suspect there is some other function of the two cards I must take.
That's about where I am now.
Practical Question
In the land of Calizonia, casinos may not use dice in craps, but they may use cards. They must draw two cards, without replacement, from a seven card deck and add the results. The probabilities must match those with two dice. There are no regulations on what can be on the cards.
What should the Calizonia casino do?
Quote: WizardI agree with Charlie on four cards. My answer is by trial and error.
I think this is a trick question. I suspect it is impossible if you stick with the constraints of using integers and adding the two cards.
I've tried using negative numbers and adding, but can't find a solution.
I've tried multiplying, instead of adding, but still can't find a solution.
I suspect there is some other function of the two cards I must take.
That's about where I am now.
Who said anything about the numbers having to be integers? Try having all of the numbers be {integer} + 1/2.
For example, the lowest two can be 1/2 and 3/2, so you can "roll" a 2.
Quote: ThatDonGuy...
Who said anything about the numbers having to be integers? Try having all of the numbers be {integer} + 1/2.
For example, the lowest two can be 1/2 and 3/2, so you can "roll" a 2.
Quote: ThatDonGuy
Who said anything about the numbers having to be integers? Try having all of the numbers be {integer} + 1/2.
For example, the lowest two can be 1/2 and 3/2, so you can "roll" a 2.
I tried that too and couldn't find an answer, although I guess I didn't try hard enough.
Quote: Wizard...
Practical Question
In the land of Calizonia, casinos may not use dice in craps, but they may use cards. They must draw two cards, without replacement, from a seven card deck and add the results. The probabilities must match those with two dice. There are no regulations on what can be on the cards.
What should the Calizonia casino do?
The following method works.
The cards are labeled 1 2 3 4 5 6 "same". The first card drawn determine the roll of the first die. However if the first card drawn is "same" then you start over again. The second card drawn determines the roll of the second die, except if it's the "same" then you've thrown a repeat of the first roll. Using the "same" to replace the first roll means the second roll still has an equal chance for each outcome.
Quote: charliepatrickSince if you only looked at the two cards there would be 21 permutations you must use the order. Then you have 42 combinations, so some of these must be "to try again".
The following method works.
The cards are labeled 1 2 3 4 5 6 "same". The first card drawn determine the roll of the first die. However if the first card drawn is "same" then you start over again. The second card drawn determines the roll of the second die, except if it's the "same" then you've thrown a repeat of the first roll. Using the "same" to replace the first roll means the second roll still has an equal chance for each outcome.
I agree! One of the California casinos uses this method, I forget which one.
Quote: charliepatrickEach set is 0 1 2 4.
The way to show it is to consider the binary for the numbers 1 thru 6 as 001 010 011 100 101 and 110, some which use two digits and others which use one. So picking two from 1 2 4 covers the two digit ones while 0+ another cover the others. Thus each set create the numbers 1 thru 6, so are equivalent to a regular die.
Quote: charliepatrickQuote: ThatDonGuy...
Who said anything about the numbers having to be integers? Try having all of the numbers be {integer} + 1/2.
For example, the lowest two can be 1/2 and 3/2, so you can "roll" a 2.That helps as it had to be symmetric and having the middle one being 3.5 seemed to work. Working from the top the first two have to be .5 and 1.5 (to get one 2) then two 2.5 to (get two 3's). Similarly 6.5 5.5 4.5 4.5. The rest falls out.
Correct!!
-------------------------------------------------
My wife accused me of never achieving anything because of my addiction to board games.
She must have forgotten that time I won second prize in a beauty contest.
Quote: GialmereBut wait! You recount and find there are actually nine cards available. Hmm. It occurs to you that you could number the nine cards in such a way that randomly drawing two cards from the pile of nine cards also gives an integer from 2 to 12 with the same frequency of occurrence as rolling that sum on two standard dice.
Draw two cards and sum them normally with the following caveats:
2W, 3W, 4W and 5W means pair. So, for example, 4W means 44 or 8
1W is 5, W1 is 6, 6W is 8, W6 is 9. These are the only 4 cases when the order of the cards matters
I think this works but I may be wrong
Quote: GialmereThere's only eight cards. Hmm. A ha! You can still divide the cards into two sets (piles) and number them in such a way that by drawing two cards from each pile, and adding the four cards together, you get an integer from 2 to 12 with the same frequency of occurrence as rolling that sum on two standard dice.
For each pile, draw two cards and value them by their sum as follows:
01 is 1
02 is 2
12 is 3
13 is 4
23 is 5
30 is 6 (this is the only exception to the sum rule)
So, for instance, a draw of 23 and 02 is valued at 52 or 7


