Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
Quote: rsactuaryPlaying around with this.
My first strategy (don't know if it's optimal yet) was:
If first roll is a 5 or 6, place in 100s spot. If first roll is a 1 or 2, place in the 1s spot. Else (dice roll of 3 or 4), place in 10s spot.
If second roll is 4, 5, 6 place in leftmost open spot. Else in right most open spot.
This gives an expected value of 504.
Quote: ThatDonGuyI did a simulation, and 504 does appear to be correct. I'll have to check my numbers again.
I see the problem: I was assigning the second die to the higher value on a 3-6 instead of a 4-6.
Now I get 504, and 503.625 for assigning a first die of 3 to 1 instead of 10.
Quote: charliepatrickAgree - I did play around a bit more using a spreadsheet and your idea gives 504. Putting 3's into the Units Columns gives 503.625. Only keeping 6s is 492.75.
Correct!!!
:strip_icc()/pic6198361.png)
:strip_icc()/pic6198360.png)
A four digit version would interesting.
-----------------------------------------------
Quote: ThatDonGuyCould somebody point me to the post where this particular version of the problem is stated? I have a feeling it's a misinterpretation of the three-level one
2 7 6 / 5 4 3 1 0
3 5 6 / 7 4 2 1 0
3 5 7 / 4 6 2 1 0
3 5 7 / 6 2 4 1 0
3 6 5 / 7 4 1 2 0
3 6 5 / 7 4 2 0 1
3 6 7 / 2 5 4 1 0
3 6 7 / 4 2 5 0 1
3 6 7 / 4 5 0 1 2
3 6 7 / 5 2 1 4 0
3 7 4 / 5 6 2 1 0
3 7 4 / 6 5 1 2 0
3 7 4 / 6 5 2 0 1
3 7 5 / 6 1 4 2 0
3 7 5 / 6 4 0 1 2
3 7 6 / 2 4 5 1 0
3 7 6 / 2 5 4 0 1
3 7 6 / 4 1 5 2 0
3 7 6 / 5 1 2 4 0
3 7 6 / 5 1 4 0 2
4 5 6 / 3 7 1 2 0
4 5 6 / 3 7 2 0 1
4 5 6 / 7 1 3 0 2
4 5 6 / 7 2 0 3 1
4 5 7 / 2 6 1 3 0
4 5 7 / 3 2 6 1 0
4 5 7 / 3 6 0 1 2
4 5 7 / 6 0 2 3 1
4 5 7 / 6 0 3 1 2
4 5 7 / 6 1 2 0 3
4 5 7 / 6 2 0 1 3
4 6 3 / 7 5 2 1 0
4 6 5 / 2 7 3 1 0
4 6 5 / 7 0 3 2 1
4 6 5 / 7 2 1 0 3
4 6 7 / 2 1 5 3 0
4 6 7 / 2 3 1 5 0
4 6 7 / 2 5 0 1 3
4 6 7 / 3 0 5 2 1
4 6 7 / 3 1 2 5 0
4 6 7 / 5 0 1 2 3
4 7 3 / 6 2 5 1 0
4 7 3 / 6 5 0 2 1
4 7 3 / 6 5 1 0 2
4 7 5 / 1 6 2 3 0
4 7 5 / 2 3 6 0 1
4 7 5 / 2 6 0 3 1
4 7 5 / 3 1 6 2 0
4 7 5 / 6 0 1 3 2
4 7 5 / 6 0 2 1 3
4 7 5 / 6 1 0 2 3
4 7 6 / 0 5 3 2 1
4 7 6 / 1 2 5 3 0
4 7 6 / 1 3 5 0 2
4 7 6 / 1 5 2 0 3
4 7 6 / 3 0 5 1 2
4 7 6 / 3 2 0 5 1
5 3 6 / 7 2 4 1 0
5 3 7 / 6 1 4 2 0
5 3 7 / 6 4 0 1 2
5 4 6 / 2 7 3 1 0
5 4 6 / 7 0 3 2 1
5 4 6 / 7 2 1 0 3
5 4 7 / 1 6 3 2 0
5 4 7 / 2 3 6 1 0
5 4 7 / 3 2 6 0 1
5 4 7 / 6 1 0 3 2
5 6 2 / 7 3 4 1 0
5 6 2 / 7 4 3 0 1
5 6 3 / 7 2 1 4 0
5 6 4 / 2 7 1 3 0
5 6 4 / 3 7 0 1 2
5 6 4 / 7 1 0 3 2
5 6 7 / 0 2 3 4 1
5 6 7 / 0 4 1 2 3
5 6 7 / 1 2 3 0 4
5 6 7 / 3 0 1 2 4
5 7 2 / 3 6 4 1 0
5 7 2 / 4 6 1 3 0
5 7 2 / 6 3 1 4 0
5 7 2 / 6 4 0 3 1
5 7 3 / 2 4 6 1 0
5 7 3 / 4 1 6 2 0
5 7 3 / 6 0 4 1 2
5 7 4 / 1 3 6 2 0
5 7 4 / 2 6 0 1 3
5 7 4 / 3 1 6 0 2
5 7 6 / 0 2 4 1 3
5 7 6 / 0 3 1 4 2
5 7 6 / 1 0 4 3 2
5 7 6 / 1 3 0 2 4
5 7 6 / 2 0 3 1 4
5 7 6 / 2 1 0 4 3
6 2 7 / 3 5 4 1 0
6 2 7 / 4 3 5 1 0
6 2 7 / 4 5 1 3 0
6 3 4 / 7 5 1 2 0
6 3 4 / 7 5 2 0 1
6 3 5 / 4 7 1 2 0
6 3 5 / 4 7 2 0 1
6 3 5 / 7 1 4 2 0
6 3 5 / 7 4 0 1 2
6 3 7 / 1 5 4 2 0
6 3 7 / 2 5 1 4 0
6 3 7 / 4 1 5 0 2
6 3 7 / 4 2 1 5 0
6 3 7 / 5 0 4 1 2
6 4 3 / 5 7 2 1 0
6 4 5 / 2 7 1 3 0
6 4 5 / 3 7 0 1 2
6 4 5 / 7 1 0 3 2
6 4 7 / 0 5 2 3 1
6 4 7 / 0 5 3 1 2
6 4 7 / 1 3 2 5 0
6 4 7 / 1 5 0 3 2
6 4 7 / 2 1 3 5 0
6 4 7 / 2 3 0 5 1
6 5 2 / 7 3 4 0 1
6 5 2 / 7 4 1 3 0
6 5 3 / 4 7 0 2 1
6 5 3 / 4 7 1 0 2
6 5 3 / 7 1 2 4 0
6 5 3 / 7 1 4 0 2
6 5 4 / 1 7 3 2 0
6 5 4 / 3 2 7 1 0
6 5 4 / 7 0 1 3 2
6 5 4 / 7 0 2 1 3
6 5 4 / 7 1 0 2 3
6 5 7 / 0 2 4 1 3
6 5 7 / 0 3 1 4 2
6 5 7 / 1 0 4 3 2
6 5 7 / 1 3 0 2 4
6 5 7 / 2 0 3 1 4
6 5 7 / 2 1 0 4 3
6 7 1 / 3 5 4 2 0
6 7 1 / 4 3 5 2 0
6 7 1 / 4 5 3 0 2
6 7 1 / 5 2 4 3 0
6 7 1 / 5 3 2 4 0
6 7 1 / 5 3 4 0 2
6 7 2 / 3 4 1 5 0
6 7 2 / 3 5 0 4 1
6 7 2 / 5 0 4 3 1
6 7 2 / 5 1 4 0 3
6 7 2 / 5 3 1 0 4
6 7 3 / 0 5 4 2 1
6 7 3 / 1 4 2 5 0
6 7 3 / 2 1 5 4 0
6 7 3 / 2 4 0 5 1
6 7 3 / 2 5 1 0 4
6 7 3 / 4 0 2 5 1
6 7 3 / 5 0 2 1 4
6 7 3 / 5 1 0 2 4
6 7 4 / 0 2 5 3 1
6 7 4 / 0 5 1 2 3
6 7 4 / 2 0 3 5 1
6 7 4 / 2 0 5 1 3
6 7 4 / 2 3 1 0 5
6 7 4 / 3 0 1 5 2
6 7 4 / 3 1 2 0 5
6 7 4 / 3 2 0 1 5
6 7 5 / 0 1 3 4 2
6 7 5 / 0 1 4 2 3
6 7 5 / 0 2 3 1 4
6 7 5 / 0 3 1 2 4
6 7 5 / 1 2 0 3 4
6 7 5 / 2 0 1 3 4
7 2 4 / 6 5 3 1 0
7 2 5 / 4 6 3 0 1
7 2 6 / 3 4 5 0 1
7 2 6 / 4 5 0 3 1
7 2 6 / 5 1 4 3 0
7 2 6 / 5 4 1 0 3
7 3 4 / 5 2 6 1 0
7 3 4 / 5 6 0 1 2
7 3 4 / 6 1 5 2 0
7 3 5 / 2 4 6 1 0
7 3 5 / 4 1 6 2 0
7 3 5 / 6 0 4 1 2
7 3 6 / 1 5 2 4 0
7 3 6 / 1 5 4 0 2
7 3 6 / 2 4 1 5 0
7 3 6 / 2 5 0 4 1
7 3 6 / 4 0 5 1 2
7 3 6 / 4 2 0 5 1
7 3 6 / 5 1 0 4 2
7 3 6 / 5 1 2 0 4
7 3 6 / 5 2 0 1 4
7 4 2 / 5 6 3 0 1
7 4 2 / 6 3 5 1 0
7 4 2 / 6 5 1 3 0
7 4 3 / 5 2 6 0 1
7 4 5 / 0 6 3 2 1
7 4 5 / 1 6 2 0 3
7 4 5 / 2 1 6 3 0
7 4 5 / 3 0 6 2 1
7 4 5 / 3 2 1 6 0
7 4 6 / 0 3 5 1 2
7 4 6 / 0 5 1 3 2
7 4 6 / 0 5 2 1 3
7 4 6 / 1 2 5 0 3
7 4 6 / 3 1 0 5 2
7 4 6 / 3 2 1 0 5
7 5 1 / 6 3 4 2 0
7 5 1 / 6 4 2 3 0
7 5 2 / 3 4 6 1 0
7 5 2 / 4 3 6 0 1
7 5 2 / 4 6 0 3 1
7 5 2 / 6 1 3 4 0
7 5 2 / 6 3 0 4 1
7 5 2 / 6 4 0 1 3
7 5 3 / 4 1 6 0 2
7 5 3 / 6 1 0 4 2
7 5 3 / 6 1 2 0 4
7 5 3 / 6 2 0 1 4
7 5 4 / 0 6 2 3 1
7 5 4 / 0 6 3 1 2
7 5 4 / 1 2 6 3 0
7 5 4 / 1 3 6 0 2
7 5 4 / 1 6 0 3 2
7 5 4 / 2 3 1 6 0
7 5 4 / 3 0 6 1 2
7 5 4 / 3 1 2 6 0
7 5 6 / 0 1 3 4 2
7 5 6 / 0 1 4 2 3
7 5 6 / 0 2 3 1 4
7 5 6 / 0 3 1 2 4
7 5 6 / 1 2 0 3 4
7 5 6 / 2 0 1 3 4
7 6 1 / 3 4 5 2 0
7 6 1 / 5 2 3 4 0
7 6 1 / 5 4 2 0 3
7 6 2 / 1 5 4 3 0
7 6 2 / 4 1 3 5 0
7 6 2 / 4 3 0 5 1
7 6 2 / 5 0 3 4 1
7 6 2 / 5 3 0 1 4
7 6 3 / 0 4 5 2 1
7 6 3 / 0 5 4 1 2
7 6 3 / 1 2 5 4 0
7 6 3 / 2 1 4 5 0
7 6 3 / 2 5 0 1 4
7 6 3 / 4 1 0 5 2
7 6 3 / 4 2 1 0 5
7 6 3 / 5 0 1 2 4
7 6 4 / 0 3 2 5 1
7 6 4 / 1 3 0 5 2
7 6 4 / 2 3 0 1 5
7 6 5 / 0 2 1 4 3
7 6 5 / 1 0 2 4 3
7 6 5 / 1 0 3 2 4
0 2 7 6 / 5 4 3 1
0 3 5 6 / 7 4 2 1
0 3 5 7 / 4 6 2 1
0 3 5 7 / 6 2 4 1
0 3 6 5 / 7 4 1 2
0 3 6 7 / 2 5 4 1
0 3 6 7 / 5 2 1 4
0 3 7 4 / 5 6 2 1
0 3 7 4 / 6 5 1 2
0 3 7 5 / 6 1 4 2
0 3 7 6 / 2 4 5 1
0 3 7 6 / 4 1 5 2
0 3 7 6 / 5 1 2 4
0 4 5 6 / 3 7 1 2
0 4 5 7 / 2 6 1 3
0 4 5 7 / 3 2 6 1
0 4 6 3 / 7 5 2 1
0 4 6 5 / 2 7 3 1
0 4 6 7 / 2 1 5 3
0 4 6 7 / 2 3 1 5
0 4 6 7 / 3 1 2 5
0 4 7 3 / 6 2 5 1
0 4 7 5 / 1 6 2 3
0 4 7 5 / 3 1 6 2
0 4 7 6 / 1 2 5 3
0 5 3 6 / 7 2 4 1
0 5 3 7 / 6 1 4 2
0 5 4 6 / 2 7 3 1
0 5 4 7 / 1 6 3 2
0 5 4 7 / 2 3 6 1
0 5 6 2 / 7 3 4 1
0 5 6 3 / 7 2 1 4
0 5 6 4 / 2 7 1 3
0 5 7 2 / 3 6 4 1
0 5 7 2 / 4 6 1 3
0 5 7 2 / 6 3 1 4
0 5 7 3 / 2 4 6 1
0 5 7 3 / 4 1 6 2
0 5 7 4 / 1 3 6 2
0 6 2 7 / 3 5 4 1
0 6 2 7 / 4 3 5 1
0 6 2 7 / 4 5 1 3
0 6 3 4 / 7 5 1 2
0 6 3 5 / 4 7 1 2
0 6 3 5 / 7 1 4 2
0 6 3 7 / 1 5 4 2
0 6 3 7 / 2 5 1 4
0 6 3 7 / 4 2 1 5
0 6 4 3 / 5 7 2 1
0 6 4 5 / 2 7 1 3
0 6 4 7 / 1 3 2 5
0 6 4 7 / 2 1 3 5
0 6 5 2 / 7 4 1 3
0 6 5 3 / 7 1 2 4
0 6 5 4 / 1 7 3 2
0 6 5 4 / 3 2 7 1
0 6 7 1 / 3 5 4 2
0 6 7 1 / 4 3 5 2
0 6 7 1 / 5 2 4 3
0 6 7 1 / 5 3 2 4
0 6 7 2 / 3 4 1 5
0 6 7 3 / 1 4 2 5
0 6 7 3 / 2 1 5 4
0 7 2 4 / 6 5 3 1
0 7 2 6 / 5 1 4 3
0 7 3 4 / 5 2 6 1
0 7 3 4 / 6 1 5 2
0 7 3 5 / 2 4 6 1
0 7 3 5 / 4 1 6 2
0 7 3 6 / 1 5 2 4
0 7 3 6 / 2 4 1 5
0 7 4 2 / 6 3 5 1
0 7 4 2 / 6 5 1 3
0 7 4 5 / 2 1 6 3
0 7 4 5 / 3 2 1 6
0 7 5 1 / 6 3 4 2
0 7 5 1 / 6 4 2 3
0 7 5 2 / 3 4 6 1
0 7 5 2 / 6 1 3 4
0 7 5 4 / 1 2 6 3
0 7 5 4 / 2 3 1 6
0 7 5 4 / 3 1 2 6
0 7 6 1 / 3 4 5 2
0 7 6 1 / 5 2 3 4
0 7 6 2 / 1 5 4 3
0 7 6 2 / 4 1 3 5
0 7 6 3 / 1 2 5 4
0 7 6 3 / 2 1 4 5
1 2 6 5 / 7 4 0 3
1 2 6 7 / 3 5 0 4
1 2 6 7 / 5 0 4 3
1 2 7 4 / 6 5 0 3
1 2 7 6 / 4 3 0 5
1 2 7 6 / 5 0 3 4
1 3 4 6 / 5 7 0 2
1 3 5 4 / 7 6 0 2
1 3 5 6 / 7 0 2 4
1 3 5 7 / 2 6 0 4
1 3 5 7 / 4 0 6 2
1 3 6 7 / 0 5 2 4
1 3 7 4 / 5 0 6 2
1 3 7 5 / 0 6 4 2
1 3 7 5 / 4 2 0 6
1 3 7 6 / 2 0 5 4
1 4 3 5 / 7 6 0 2
1 4 3 7 / 6 0 5 2
1 4 5 6 / 0 7 2 3
1 4 5 6 / 3 0 7 2
1 4 5 7 / 3 0 2 6
1 4 6 3 / 7 2 0 5
1 4 7 2 / 6 3 0 5
1 4 7 3 / 5 2 0 6
1 4 7 5 / 2 0 3 6
1 5 2 6 / 7 3 0 4
1 5 2 7 / 6 0 4 3
1 5 3 7 / 0 6 4 2
1 5 3 7 / 4 2 0 6
1 5 4 7 / 0 2 6 3
1 5 6 2 / 3 7 0 4
1 5 6 3 / 0 7 4 2
1 5 6 4 / 0 3 7 2
1 5 6 4 / 2 0 7 3
1 5 6 4 / 3 2 0 7
1 5 7 0 / 4 6 3 2
1 5 7 2 / 3 4 0 6
1 5 7 3 / 2 0 6 4
1 5 7 4 / 0 2 3 6
1 6 2 5 / 7 0 4 3
1 6 2 7 / 4 0 3 5
1 6 3 5 / 4 0 7 2
1 6 3 7 / 0 2 5 4
1 6 4 3 / 7 0 2 5
1 6 4 5 / 0 3 7 2
1 6 4 5 / 2 0 7 3
1 6 4 5 / 3 2 0 7
1 6 5 0 / 7 4 3 2
1 6 5 4 / 2 3 0 7
1 6 7 0 / 2 5 4 3
1 6 7 0 / 4 3 2 5
1 6 7 2 / 0 3 4 5
1 7 0 6 / 4 5 3 2
1 7 0 6 / 5 3 4 2
1 7 0 6 / 5 4 2 3
1 7 2 3 / 6 5 0 4
1 7 2 4 / 6 0 5 3
1 7 2 5 / 4 0 6 3
1 7 2 5 / 4 3 0 6
1 7 2 6 / 0 4 5 3
1 7 2 6 / 0 5 3 4
1 7 2 6 / 3 0 4 5
1 7 3 2 / 5 6 0 4
1 7 3 4 / 0 6 5 2
1 7 3 4 / 5 0 2 6
1 7 3 5 / 2 0 6 4
1 7 4 0 / 6 5 3 2
1 7 4 2 / 3 6 0 5
1 7 4 2 / 5 0 6 3
1 7 4 2 / 5 3 0 6
1 7 4 2 / 6 0 3 5
1 7 4 3 / 0 5 6 2
1 7 4 3 / 2 5 0 6
1 7 5 0 / 3 6 4 2
1 7 5 0 / 6 2 3 4
1 7 5 2 / 0 6 3 4
1 7 5 2 / 3 0 6 4
1 7 5 2 / 4 0 3 6
1 7 5 3 / 0 2 6 4
1 7 5 3 / 0 4 2 6
1 7 5 3 / 2 0 4 6
1 7 6 0 / 2 4 5 3
1 7 6 0 / 2 5 3 4
1 7 6 0 / 3 4 2 5
1 7 6 0 / 4 2 3 5
2 0 7 6 / 5 4 1 3
2 1 5 6 / 7 4 0 3
2 1 5 7 / 4 6 0 3
2 1 5 7 / 6 3 0 4
2 1 6 7 / 4 3 0 5
2 1 6 7 / 5 0 3 4
2 1 7 4 / 5 6 0 3
2 1 7 5 / 6 0 4 3
2 1 7 6 / 3 4 0 5
2 1 7 6 / 4 0 5 3
2 3 4 7 / 5 0 1 6
2 3 5 6 / 0 7 1 4
2 3 6 5 / 4 1 0 7
2 3 7 1 / 6 5 0 4
2 3 7 4 / 0 6 1 5
2 3 7 4 / 1 5 0 6
2 3 7 5 / 0 1 6 4
2 4 1 7 / 5 6 0 3
2 4 3 7 / 1 6 0 5
2 4 5 1 / 7 6 0 3
2 4 5 3 / 7 1 0 6
2 4 6 0 / 7 5 1 3
2 4 6 1 / 7 3 0 5
2 4 6 3 / 1 7 0 5
2 4 6 3 / 5 1 0 7
2 4 6 5 / 0 3 1 7
2 4 7 1 / 3 6 0 5
2 4 7 1 / 5 0 6 3
2 4 7 1 / 5 3 0 6
2 4 7 1 / 6 0 3 5
2 4 7 3 / 0 5 1 6
2 5 1 6 / 7 0 4 3
2 5 3 4 / 7 1 0 6
2 5 3 6 / 4 0 1 7
2 5 3 7 / 0 1 6 4
2 5 4 1 / 6 7 0 3
2 5 4 3 / 7 0 1 6
2 5 4 6 / 0 3 1 7
2 5 6 3 / 1 0 7 4
2 5 6 4 / 0 1 3 7
2 5 7 0 / 1 6 4 3
2 5 7 0 / 4 3 1 6
2 5 7 1 / 0 4 6 3
2 6 0 7 / 4 1 5 3
2 6 0 7 / 4 3 1 5
2 6 1 5 / 3 7 0 4
2 6 1 7 / 0 4 5 3
2 6 1 7 / 0 5 3 4
2 6 1 7 / 3 0 4 5
2 6 3 1 / 7 5 0 4
2 6 3 4 / 5 0 1 7
2 6 3 5 / 1 4 0 7
2 6 4 0 / 5 7 1 3
2 6 4 3 / 0 7 1 5
2 6 4 5 / 0 1 3 7
2 6 5 0 / 3 7 1 4
2 6 5 1 / 4 0 7 3
2 6 5 3 / 0 1 7 4
2 6 5 3 / 0 4 1 7
2 7 0 5 / 3 6 1 4
2 7 0 6 / 1 5 4 3
2 7 0 6 / 4 1 3 5
2 7 1 3 / 6 4 0 5
2 7 1 4 / 3 6 0 5
2 7 1 4 / 5 0 6 3
2 7 1 4 / 5 3 0 6
2 7 1 4 / 6 0 3 5
2 7 1 5 / 0 6 4 3
2 7 1 6 / 0 3 5 4
2 7 1 6 / 0 4 3 5
2 7 3 0 / 6 5 1 4
2 7 3 1 / 4 6 0 5
2 7 3 4 / 1 0 6 5
2 7 4 0 / 5 1 6 3
2 7 4 0 / 6 1 3 5
2 7 4 1 / 5 0 3 6
2 7 4 3 / 0 1 6 5
2 7 4 3 / 1 0 5 6
2 7 5 0 / 1 4 6 3
2 7 5 0 / 3 1 6 4
2 7 5 0 / 4 1 3 6
2 7 5 1 / 0 3 6 4
3 0 5 7 / 6 2 1 4
3 0 6 7 / 2 5 1 4
3 0 6 7 / 4 2 1 5
3 0 7 6 / 4 1 2 5
3 1 4 7 / 6 2 0 5
3 1 5 7 / 4 2 0 6
3 1 6 4 / 7 2 0 5
3 1 6 5 / 2 7 0 4
3 1 6 7 / 0 4 2 5
3 1 6 7 / 2 0 4 5
3 1 7 4 / 5 2 0 6
3 1 7 5 / 0 6 2 4
3 1 7 5 / 2 4 0 6
3 1 7 5 / 4 0 2 6
3 1 7 6 / 0 2 5 4
3 2 4 7 / 1 6 0 5
3 2 5 6 / 4 1 0 7
3 2 5 7 / 0 4 1 6
3 2 5 7 / 1 0 6 4
3 2 6 5 / 4 0 1 7
3 2 7 1 / 5 6 0 4
3 2 7 5 / 1 0 4 6
3 4 1 7 / 5 2 0 6
3 4 2 5 / 7 1 0 6
3 4 2 7 / 0 6 1 5
3 4 2 7 / 1 5 0 6
3 4 5 1 / 7 2 0 6
3 4 5 2 / 6 1 0 7
3 4 6 1 / 5 2 0 7
3 4 7 2 / 0 1 6 5
3 4 7 2 / 1 0 5 6
3 5 1 7 / 2 0 6 4
3 5 2 6 / 1 4 0 7
3 5 2 7 / 0 1 4 6
3 5 4 2 / 6 0 1 7
3 5 6 0 / 4 2 1 7
3 5 6 2 / 1 0 4 7
3 5 7 0 / 1 2 4 6
3 6 0 4 / 7 2 1 5
3 6 0 5 / 2 7 1 4
3 6 0 7 / 1 2 4 5
3 6 1 4 / 2 7 0 5
3 6 2 1 / 5 7 0 4
3 6 2 1 / 7 4 0 5
3 6 2 5 / 0 1 7 4
3 6 2 5 / 0 4 1 7
3 6 4 1 / 5 0 2 7
3 6 5 0 / 4 1 2 7
3 6 5 1 / 0 2 7 4
3 6 5 2 / 0 1 4 7
3 7 0 2 / 6 5 1 4
3 7 0 4 / 2 6 1 5
3 7 0 4 / 5 1 2 6
3 7 0 5 / 2 1 6 4
3 7 1 2 / 5 4 0 6
3 7 1 2 / 6 0 5 4
3 7 1 5 / 0 2 4 6
3 7 2 0 / 6 4 1 5
3 7 2 1 / 4 5 0 6
3 7 2 1 / 6 0 4 5
3 7 2 4 / 0 1 5 6
3 7 4 0 / 1 5 2 6
3 7 4 1 / 0 2 6 5
4 0 7 3 / 6 2 1 5
4 0 7 5 / 2 3 1 6
4 0 7 5 / 3 1 2 6
4 1 3 6 / 7 2 0 5
4 1 3 7 / 6 0 2 5
4 1 5 6 / 3 2 0 7
4 1 5 7 / 0 3 2 6
4 1 6 2 / 7 3 0 5
4 1 6 5 / 2 3 0 7
4 1 7 2 / 3 6 0 5
4 1 7 2 / 5 3 0 6
4 1 7 2 / 6 0 3 5
4 1 7 3 / 2 5 0 6
4 2 3 5 / 7 1 0 6
4 2 3 7 / 0 6 1 5
4 2 3 7 / 1 5 0 6
4 2 5 6 / 1 0 3 7
4 2 6 3 / 0 7 1 5
4 2 6 5 / 0 1 3 7
4 2 7 1 / 3 5 0 6
4 2 7 3 / 1 0 6 5
4 3 1 6 / 7 0 2 5
4 3 1 7 / 2 6 0 5
4 3 2 5 / 7 0 1 6
4 3 2 6 / 1 7 0 5
4 3 2 6 / 5 1 0 7
4 3 5 2 / 6 0 1 7
4 3 6 2 / 1 5 0 7
4 3 7 0 / 1 6 2 5
4 3 7 0 / 2 5 1 6
4 3 7 1 / 0 5 2 6
4 3 7 1 / 2 0 6 5
4 3 7 2 / 0 1 5 6
4 5 0 7 / 1 2 3 6
4 5 1 6 / 2 0 3 7
4 5 3 1 / 6 2 0 7
4 5 3 2 / 1 7 0 6
4 6 0 2 / 7 3 1 5
4 6 0 5 / 2 3 1 7
4 6 0 5 / 3 1 2 7
4 6 1 3 / 5 0 2 7
4 6 1 5 / 0 2 3 7
4 6 2 0 / 7 1 3 5
4 6 2 1 / 5 3 0 7
4 6 2 3 / 0 5 1 7
4 6 3 0 / 5 2 1 7
4 6 3 2 / 1 0 7 5
4 7 0 1 / 6 3 2 5
4 7 1 0 / 6 2 3 5
4 7 1 2 / 0 6 3 5
4 7 1 2 / 3 0 6 5
4 7 1 3 / 0 2 6 5
4 7 2 1 / 3 0 5 6
4 7 3 0 / 1 2 6 5
4 7 3 0 / 2 1 5 6
5 0 4 7 / 2 3 1 6
5 0 4 7 / 3 1 2 6
5 0 7 3 / 2 4 1 6
5 0 7 4 / 1 2 3 6
5 1 2 7 / 4 3 0 6
5 1 4 6 / 3 0 2 7
5 1 6 3 / 2 4 0 7
5 1 6 3 / 4 0 2 7
5 1 6 4 / 2 0 3 7
5 1 7 2 / 3 0 4 6
5 1 7 3 / 0 2 4 6
5 2 1 7 / 3 4 0 6
5 2 3 4 / 6 1 0 7
5 2 4 3 / 6 0 1 7
5 2 6 1 / 3 4 0 7
5 2 6 3 / 1 0 4 7
5 2 7 1 / 0 4 3 6
5 3 0 7 / 4 1 2 6
5 3 1 4 / 7 2 0 6
5 3 1 7 / 0 4 2 6
5 3 1 7 / 2 0 4 6
5 3 2 4 / 6 0 1 7
5 3 2 6 / 0 4 1 7
5 3 4 1 / 6 2 0 7
5 3 4 2 / 1 7 0 6
5 3 6 0 / 2 4 1 7
5 3 6 1 / 0 4 2 7
5 3 6 1 / 2 0 4 7
5 4 0 6 / 3 2 1 7
5 4 1 3 / 7 0 2 6
5 4 1 6 / 0 3 2 7
5 4 2 1 / 7 3 0 6
5 4 2 3 / 1 7 0 6
5 4 3 0 / 7 2 1 6
5 6 0 3 / 2 4 1 7
5 6 0 4 / 1 2 3 7
5 6 2 0 / 3 4 1 7
5 6 2 1 / 3 0 4 7
5 6 3 0 / 2 1 4 7
5 7 0 2 / 1 3 4 6
5 7 1 0 / 2 4 3 6
5 7 1 0 / 3 2 4 6
6 0 5 4 / 3 2 1 7
6 1 3 4 / 5 2 0 7
6 1 3 5 / 2 4 0 7
6 1 3 5 / 4 0 2 7
6 1 4 5 / 0 3 2 7
6 1 5 2 / 3 4 0 7
6 1 5 4 / 0 2 3 7
6 2 3 5 / 1 0 4 7
6 2 4 1 / 5 3 0 7
6 2 4 3 / 0 5 1 7
6 2 5 1 / 4 0 3 7
6 3 1 4 / 5 0 2 7
6 3 2 4 / 0 5 1 7
6 3 2 5 / 0 1 4 7
6 3 4 0 / 5 1 2 7
6 3 5 0 / 1 4 2 7
6 3 5 1 / 0 2 4 7
6 4 0 5 / 1 3 2 7
6 4 0 5 / 2 1 3 7
6 4 2 1 / 3 5 0 7
6 4 3 2 / 1 0 5 7
6 5 0 2 / 4 3 1 7
6 5 1 2 / 3 0 4 7
6 5 1 3 / 0 2 4 7
6 5 2 0 / 4 1 3 7
6 5 3 0 / 1 2 4 7
There is no original problem. Let me just make one now.
Consider an 8-inch long scale bar with 9 marks equally gapped by one inch. There are also 7 weights, each weighing 1, 2, 3, 4, 5, 6, and 7 ounces, respectively. You will tie a pivot hook and all these 7 weights on the 9 marks to balance the scale bar. At each mark, you can only tie a hook or a weight once, or leave it empty. How to tie?
I complied your solutions. If the hook is at the center, there are 441 ways to tie; if the hook is one inch off center, there are 251 ways to tie.
:strip_icc()/pic6192893.png)
Find your way through the number maze.
You begin the logic maze above in the upper left red square and try to make it to the lower right "Goal" square. The number you are on tells you how many squares you MUST traverse -- in either the horizontal or vertical direction -- on your next move.
Assume the top row is, from left to right, labeled A1 to A5. The next row is B1 to B5 etc. So your first move will be 4 squares from either A1 to A5 or A1 to E1. In both cases the next move will be 3 squares (and so on).
Answer with your path through the maze: A1, . . ., Goal
I can find two solutions (easiest done by working backwards):
A1, E1, B1, B3, D3, A3, C3, E3, Goal
A1, E1, B1, B3, D3, A3, C3, C5, Goal
Quote: ThatDonGuy
I can find two solutions (easiest done by working backwards):
A1, E1, B1, B3, D3, A3, C3, E3, Goal
A1, E1, B1, B3, D3, A3, C3, C5, Goal
Correct!
---------------------------------------
I'm surrounded by idiots.
Unfortunately, I am currently stuck in a mirror maze.
---------------------------------------
MEMORIAL DAY BONUS!
Too easy? Well...
Try a 6x6!
:strip_icc()/pic6203301.png)
(i) Working backwards the blue centre square and cross (and other blues in columns 1 3 and 5, get you to the goal using the 2's (avoid the 3s as they get you back to green). Thus the aim is to get to A3 (from whence you go C3 and either route (C5/E3) to goal.
(ii) There are four blue squares in columns 2 and 4; these need to be avoided since, having 2s, they only point at each other; so you can't get out from them.
(iii) Thus way from Green to the above has to be via A3, hence you come from D3. Note that the greens also have two parts.
(iv) The Greens on Rows 2 and 4 (using the 2s and avoiding the 3s, could reach D3).
(v) The Greens on Rows 1 3 and 5 cannot reach D3 - so these should be avoided.
(vi) Now see how you get from the start onto the correct set of green squares and avoiding the 3s, this can only be achieved by going via E1 and B1. (There are four first moves (EW, ES, SN, SW), and the others don't work).
(vii) So the start is A1 E1 B1, the green bit to blue is B1 B3 D3 A3, and the last bit is A3 C3 (C5/E3) E5.
A1 A6 E6 E2 B2 B5 D5 F5 C5 C1 B1 B4 F4 End
Quote: charliepatrickThe only way is to work backwards (and accept you go up some loops) to get
A1 A6 E6 E2 B2 B5 D5 F5 C5 C1 B1 B4 F4 End
Correct!
There's a fun, multi-state version of this type of logic maze which I'll save for a future toughie Tuesday.
--------------------------------------


Can you create a set of dials that meet the following requirements?
There are six dials, each with four values. Each value is a unique positive integer (for a total 24 unique values.)
The dials are arranged left to right. The first two dials spin freely. The other dials may only turn to a new value if the two previous dials sum to that value.
There are no unused values. There exists some way for each dial to turn to all four of its values, and the values on the first two dials can all be used in a sum. (The first dial's values can all be used with values from the second dial to obtain a sum on the third dial. The values on the second dial can be used to obtain a sum on either the third or fourth dial. For example, the first three dials could be: {1,2,3,4}; {5,6,7,8}; {9,10,11,12}. The {1,2,3,4} can be summed with {8,7,6,5} to obtain "9" on the third dial, and the {10,11,12} can all be obtained through other sums.)
The largest value (of all 24) is as small as possible.
Here is a solution where the largest value is 25:
1, 2, 7, 11
3, 4, 12, 20
5 (1,4), 6 (2,4), 13 (1,12) ,19 (7,12)
8 (3,5), 9 (4,5), 10 (4,6), 17 (4,13)
14 (5,9), 15 (6,9), 16 (6,10), 21 (13,8)
22 (8,14), 23 (9,14), 24 (9,15), 25 (9,16)
Do I hear bids for a perfect 24?
Quote: GialmereThatDonGuy has solved for 26 and 25.
Do I hear bids for a perfect 24?
1 2 3 8 12 20
4 5 7 9 15 21
11 6 10 16 18 23
13 14 17 22 19 24
The method I used, trial and error, except that to get an 8 requires 1 2 3 with a 5 in the 2nd column. Then I was working backwards but also seeing that, say 10, needs a 1 2 3 or 4, so you couldn't have used them all elsewhere.
Quote: charliepatrick1 2 3 8 12 20
4 5 7 9 15 21
11 6 10 16 18 23
13 14 17 22 19 24
The method I used, trial and error, except that to get an 8 requires 1 2 3 with a 5 in the 2nd column. Then I was working backwards but also seeing that, say 10, needs a 1 2 3 or 4, so you couldn't have used them all elsewhere.
This "machine" works, however, it does not match the criteria since the 13 on dial #1 is an unused value.
Note: You can place numbers on the dials anywhere you want.
:strip_icc()/pic6208536.png)
You step out of the time machine into Vegas of the future. It somehow appears both immediately recognizable and totally alien.
You enter a casino and find it filled with slot machines (they're still around of course) but no live table games. In fact, the only real humans working here seem to be the ones that fix the machines. Even the escort girls are androids.
You approach a machine with a large video screen filled with numbers. At first you think it's some sort of keno game but find it's actually a futuristic version of craps played with a pair of one million sided dice. To your surprise, the rules are recognizable.
A Pass Line bet wins immediately if the Come Out roll is a 1,000,001 or a 1,999,999. It loses immediately if the Come Out roll is a 2, 3, or 2,000,000. Any other number becomes the point, and the point number must then be rolled again before a result of 1,000,001 shows up.
What is the probability of winning this Pass Line bet?
Quote: GialmereWe'll let the dials hang for another day or two. In the meantime, I'll set them for several centuries ahead...
You step out of the time machine into Vegas of the future. It somehow appears both immediately recognizable and totally alien.
You enter a casino and find it filled with slot machines (they're still around of course) but no live table games. In fact, the only real humans working here seem to be the ones that fix the machines. Even the escort girls are androids.
You approach a machine with a large video screen filled with numbers. At first you think it's some sort of keno game but find it's actually a futuristic version of craps played with a pair of one million sided dice. To your surprise, the rules are recognizable.
A Pass Line bet wins immediately if the Come Out roll is a 1,000,001 or a 1,999,999. It loses immediately if the Come Out roll is a 2, 3, or 2,000,000. Any other number becomes the point, and the point number must then be rolled again before a result of 1,000,001 shows up.
What is the probability of winning this Pass Line bet?
The numbers of ways of rolling 1,999,999 or 1,000,001 on the come out roll are 2 or 1,000,000, respectively. So, the probability of winning on the come out roll is 1,000,002 / 1012.
The number of ways of establishing a point, n, less than 1,000,001 is n - 1. And the probability of rolling another n before rolling a 1,000,001 is (n - 1) / (n - 1 + 1,000,000).
The probability of establishing and making a point, n, less than 1,000,001 is (n - 1)2 / (1012(n + 999,999)). The sum of these terms for n = 4 to n = 1,000,000 is approximately 0.193147 according to the site WolframAlpha. The probability of establishing and making a point greater than 1,000,001 would also equal this number.
So, the probability of winning a pass line bet would be 1,000,002 / 1012 + 2(0.193147) or about 0.3863.
I did it on Excel, and get 0.38621453.
I have a feeling one, or possibly both, of us has a roundoff error. I am trying to get an exact answer, but it may take a while; it took 5 minutes just to calculate the first 15,000 of the 1,000,000 terms, and it is currently running at 1000 terms a minute (and will slow down considerably). Reminds me of when I was part of GIMPS, and it took 24 hours a day for a month just to find out, "Sorry, but this one is not prime."
Update: I stopped when I discovered that the denominator will have more than 433,221 digits - that is the size of the product of all of the primes < 1,000,000
Quote: Gialmere...What is the probability of winning this Pass Line bet?
| Sided | House Edge | P(Win) |
|---|---|---|
6 | -1.414 141% | 49.292 929% |
12 | -12.463 882% | 43.768 059% |
20 | -16.908 085% | 41.545 958% |
100 | -21.700 592% | 39.149 704% |
1000 | -22.640 705% | 38.679 648% |
10000 | -22.731 124% | 38.634 438% |
100000 | -22.740 128% | 38.629 936% |
1000000 | -22.741 028% | 38.629 486% |
Today is a sequentially perfect day, it being 06.03.21, and 6 = 3 + 2 + 1 and 6 = 3*2*1.
What is the next sequentially perfect day?
What is the next perfect day? (Some rearrangement of the date fits the perfect number equations).
Quote: ThatDonGuyWhat ChesterDog said, except...
I did it on Excel, and get 0.38621453.
I checked it again, and now I get 0.386 294 861 123
Quote: teliotThis is too easy, but worthy of note in a math thread.
Today is a sequentially perfect day, it being 06.03.21, and 6 = 3 + 2 + 1 and 6 = 3*2*1.
What is the next sequentially perfect day?
What is the next perfect day? (Some rearrangement of the date fits the perfect number equations).
Neat. Iím not quite sure I understand the sequential part but it seems to me the answers are:
A "perfect number" is one that is the sum of its proper divisors. Only one of your answers fits that. But good :) And after that?Quote: unJonNeat. Iím not quite sure I understand the sequential part but it seems to me the answers are:
Next perfect: 06.12.21 then 06.21.21 then 06.30.21 and then 07.04.21. Last two seem like sequential perfects to me
2021 is a very "special" year. Perfect in many ways.
6 / 1 / 23: 6 = 1 + 2 + 3
6 / 1 / 23: 6 = 1 * 2 * 3
Quote: ChesterDog
The numbers of ways of rolling 1,999,999 or 1,000,001 on the come out roll are 2 or 1,000,000, respectively. So, the probability of winning on the come out roll is 1,000,002 / 1012.
The number of ways of establishing a point, n, less than 1,000,001 is n - 1. And the probability of rolling another n before rolling a 1,000,001 is (n - 1) / (n - 1 + 1,000,000).
The probability of establishing and making a point, n, less than 1,000,001 is (n - 1)2 / (1012(n + 999,999)). The sum of these terms for n = 4 to n = 1,000,000 is approximately 0.193147 according to the site WolframAlpha. The probability of establishing and making a point greater than 1,000,001 would also equal this number.
So, the probability of winning a pass line bet would be 1,000,002 / 1012 + 2(0.193147) or about 0.3863.
Quote: charliepatrickUsing excel spreadsheet, I get the following numbers.
Sided House Edge P(Win)
Quote: ThatDonGuyQuote: ThatDonGuyWhat ChesterDog said, except...
I did it on Excel, and get 0.38621453.
I checked it again, and now I get 0.386 294 861 123
Correct!!!
:strip_icc()/pic6209931.png)
:strip_icc()/pic6209932.png)
--------------------------------------------------------

If you think the HE for this future Pass Line bet is ridiculous, wait 'till you see the center bets.
Quote: teliotThis is too easy, but worthy of note in a math thread.
Today is a sequentially perfect day, it being 06.03.21, and 6 = 3 + 2 + 1 and 6 = 3*2*1.
What is the next sequentially perfect day?
What is the next perfect day? (Some rearrangement of the date fits the perfect number equations).
next sequentially perfect day = 06.30.21.
next perfect day (Some rearrangement of the date fits the perfect number equations) = 01.06.23
If these are considered perfect days, I misunderstood what a "perfect day" is.Quote: gordonm888
next sequentially perfect day = 06.30.21.
next perfect day (Some rearrangement of the date fits the perfect number equations) = 01.06.23
In the only example given (6.3.21), the month equaled the date plus the two digits in the year, when the date and the two digits were added or multiplied. (6 = 3+2+1 or 6 = 3x2x1)
So that's what I assumed we wanted. The month was on one side of the equation.
That doesn't work with 06.30.21 as 6 (the month) does not equal 30 + 2 + 1 nor does 6 equal 30 x 2 x 1.
That doesn't work with 01.06.23 as 1 (the month) does not equal 6 + 2 + 3 nor does 1 equal 6 x 2 x 3.
Quote: GialmereQuote: ChesterDog
The numbers of ways of rolling 1,999,999 or 1,000,001 on the come out roll are 2 or 1,000,000, respectively. So, the probability of winning on the come out roll is 1,000,002 / 1012.
The number of ways of establishing a point, n, less than 1,000,001 is n - 1. And the probability of rolling another n before rolling a 1,000,001 is (n - 1) / (n - 1 + 1,000,000).
The probability of establishing and making a point, n, less than 1,000,001 is (n - 1)2 / (1012(n + 999,999)). The sum of these terms for n = 4 to n = 1,000,000 is approximately 0.193147 according to the site WolframAlpha. The probability of establishing and making a point greater than 1,000,001 would also equal this number.
So, the probability of winning a pass line bet would be 1,000,002 / 1012 + 2(0.193147) or about 0.3863.Quote: charliepatrickUsing excel spreadsheet, I get the following numbers.
Sided House Edge P(Win) What ChesterDog said, except...
I did it on Excel, and get 0.38621453.
I checked it again, and now I get 0.386 294 861 123
Correct!!!
I tried posting the exact value for 100,000 sides (which took 3 1/2 hours to calculate, although that was only on a single thread), but the board server choked on it. What? It was only a fraction with an 86,862-digit numerator and an 86,863-digit denominator.
For 6 dials:
{2,5,7,12}, {1,9,10,11}, {3,6,8,13}, {4,14,15,16}, {17,18,19,20}, {21,22,23,24}
It is impossible to make a perfect solution for 8 or more dials.
The smallest number you can put on each dial (besides the first) is given by the following sequence:
2 1 3 4 7 11 18 29 47
Thus, the 9th dial must have numbers larger than 36.
The 8th dial can only form a perfect 8-dial solution if it contains 29, 30, 31, and 32, AND all the other numbers from the sequence are forced.
Now, note that 1 through 4 are already placed and no pair of adjacent dials adds to 5. So 5 must go on the 1st or 2nd dial. And 6 is also not formed by any pair, unless 5 goes on the 1st dial and 6 on the 3rd. The smallest remaining numbers are 8 and 9, and while it is possible to get either of these on the 4th dial by placing 5 or 6 on the 2nd, there is no way to get either of these on the 5th dial.
For the given forced values, the 2nd-smallest possible number on the 4th dial is 8 and the 2nd-smallest possible number on the 5th dial is 10. Therefore, the 2nd-smallest possible number on the 6th dial is 14 and the 2nd-smallest possible number on the 7th dial is 21. This means there is no way to make the sums 30 and 31 on the 8th dial.
So if a 6-dial solution is easy and an 8 is impossible, a perfect 7-dial solution should be just right! I have not found one yet, though having coming just one number short four times without much difficulty suggests that it should be possible.
---------------------------------------------
Fibonacci. It's as easy as 1, 1, 2, 3.
My most cited research paper is on the Fibonacci sequence ... I decided to experiment with the Fibonacci sequence modulo increasing powers of 2 and discovered that the distribution of residues stabilized at 2^5. That lead to about xxx more papers over the next 10 years that nobody cared about.Quote: GialmereFibonacci. It's as easy as 1, 1, 2, 3.
https://www.mathstat.dal.ca/FQ/Scanned/30-3/jacobson.pdf
So the answer seems to approach a limit of 0.38629... as n goes to infinity.Quote: Gialmere[
The real question is : what does that limit represent? Itís not just some random number...we can be almost certain of that
Quote: Ace2...So the answer seems to approach a limit of 0.38629... as n goes to infinity.
The real question is : what does that limit represent? Itís not just some random number...we can be almost certain of that
ln(4) - 1
Quote: ChesterDog
ln(4) - 1
This is so cool! Now I have a question from this result. Can we just say that the probability Pn is exclusively decided by the third sum term without the first two terms? Because the limits of both 1/n and 2/n^2 are zero. Thank you in advance.
Very nice. I see Ln series that resemble this dice scenario but I havenít been able to fit one exactly. Can you show how you got to ln(4) - 1 ?Quote: ChesterDog
ln(4) - 1
Quote: acesideQuote: ChesterDog
ln(4) - 1
This is so cool! Now I have a question from this result. Can we just say that the probability Pn is exclusively decided by the third sum term without the first two terms? Because the limits of both 1/n and 2/n^2 are zero. Thank you in advance.
Notice that the sum is 1 / n + 2 / n^2 + 2 / n^2 ē (3^2 / (n+3) + 4^2 / (n+4) + 5^2 / (n+5) + ... + (n-1)^2 / (2n-1))
As n approaches positive infinity, you should be able to add the terms 1^2 / (n+1) and 2^2 / (n+2) to it.
If it does equal ln 4 - 1, then the limit of 1^2 / (n^2 (n+1)) + 2^2 / (n^2 (n+2)) + 3^2 / (n^2 (n+3)) + ... should be ln 2 - 1/2.
Quote: aceside...
This is so cool! Now I have a question from this result. Can we just say that the probability Pn is exclusively decided by the third sum term without the first two terms? Because the limits of both 1/n and 2/n^2 are zero. Thank you in advance.
Quote: Ace2...Very nice. I see Ln series that resemble this dice scenario but I havenít been able to fit one exactly. Can you show how you got to ln(4) - 1 ?
Here's how I did it:

LIMIT(n->+INF) {ln (2n / (n + 3))}
= LIMIT(n->+INF) {ln ((2n + 6 - 6) / (n + 3))}
= LIMIT(n->+INF) {ln (2 - 6 / (n + 3))}
= ln 2
So yes, the limit as n approaches positive infinity of ln (2n / (3 + n)) = ln 2.
Quote: ThatDonGuyI think I have this right:
LIMIT(n->+INF) {ln (2n / (n + 3))}
= LIMIT(n->+INF) {ln ((2n + 6 - 6) / (n + 3))}
= LIMIT(n->+INF) {ln (2 - 6 / (n + 3))}
= ln 2
So yes, the limit as n approaches positive infinity of ln (2n / (3 + n)) = ln 2.
Thanks. Also, how would you prove these limits are equal?
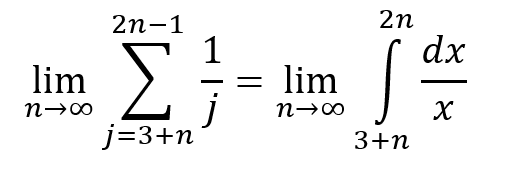

Using only pennies, nickels, dimes, quarters, half dollars, $1 bills, $5 bills, and $10 bills, what is the most money that you can have without being able to change a $20 bill?
Quote: ChesterDogThanks. Also, how would you prove these limits are equal?
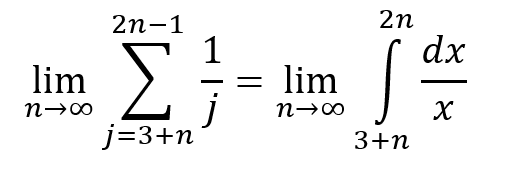

Quote: GialmereUsing only pennies, nickels, dimes, quarters, half dollars, $1 bills, $5 bills, and $10 bills, what is the most money that you can have without being able to change a $20 bill?
$20.24
There are various ways it could be done, with the following being just one:
1 quarter = $0.25
199 dimes = $19.90
9 pennies = $0.09
Total = $20.24
Quote: GialmereIt's easy Monday. Let's change things up...
g]
without being able to change a $20 bill?
Iíve read this part several times but still havenít got its exact meaning. Can you rephrase this part into precise mathematical terms?
Quote: acesideQuote: GialmereIt's easy Monday. Let's change things up...
g]
without being able to change a $20 bill?
Iíve read this part several times but still havenít got its exact meaning. Can you rephrase this part into precise mathematical terms?
You cannot make exactly $20 with any combination of bills and coins. You can have more than $20, but not exactly $20.
Quote: WizardQuote: GialmereUsing only pennies, nickels, dimes, quarters, half dollars, $1 bills, $5 bills, and $10 bills, what is the most money that you can have without being able to change a $20 bill?
$20.24
There are various ways it could be done, with the following being just one:
1 quarter = $0.25
199 dimes = $19.90
9 pennies = $0.09
Total = $20.24
Thatís a nickel higher than I get. But I think I can make change for a $20 with your coins:
1 quarter
5 pennies
Quote: unJonthatís a nickel higher than I get. But I think I can make change for a $20 with your coins:
197 dimes
1 quarter
5 pennies
You're right.
$20.19
There are various ways it could be done, with the following being just one:
1 quarter = $0.25
199 dimes = $19.90
4 pennies = $0.04
Total = $20.19
Adding 4x10c takes the total to $20.15. You cannot have anything that makes 5c, so you can only add 4x1c.
This brings to total to $20.19.
Quote: ThatDonGuyQuote: ChesterDogThanks. Also, how would you prove these limits are equal?
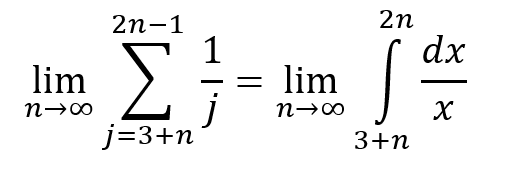

Update: I'll have to check my numbers, and there could be precision issues involved, but at the moment, it appears that the two are equal somewhere around n = 283,836,518, but for larger n, the integral slowly gets larger than the sum. Note that the difference < 10^-8 even at n = 1 billion.
Quote: unJonThatís a nickel higher than I get.
Quote: Wizard
You're right.
$20.19
There are various ways it could be done, with the following being just one:
1 quarter = $0.25
199 dimes = $19.90
4 pennies = $0.04
Total = $20.19
Quote: charliepatrickYou can make $19.75 in various means but it will include either 3x25c or 1x25c 1x50c plus $19. Any combination of coins/notes using 25c or more must be a multiple of 25c, hence their total value cannot exceed $19.75. So the important thing is it can make $19.50 or $19.75 as the highest two values. So part two of the solution has to ensure you can't get from either of these to $20.
Adding 4x10c takes the total to $20.15. You cannot have anything that makes 5c, so you can only add 4x1c.
This brings to total to $20.19.
Correct!
----------------------------------------

Quote: ThatDonGuyQuote: ThatDonGuyQuote: ChesterDogThanks. Also, how would you prove these limits are equal?
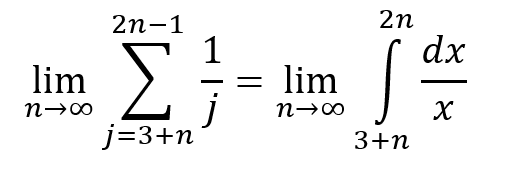

Update: I'll have to check my numbers, and there could be precision issues involved, but at the moment, it appears that the two are equal somewhere around n = 283,836,518, but for larger n, the integral slowly gets larger than the sum. Note that the difference < 10^-8 even at n = 1 billion.
Wait a minute...it's impossible for the integral to be equal to, much less greater than, the sum.
Use n = 100 as an example.
The sum is the sum of the areas of 97 rectangles, each with width 1, and heights 1/103, 1/104, 1/105, ..., 1/198, 1/199.
The integral is the sum of (the area underneath the graph y = 1/x between x = 103 and x = 104 + the area underneath the graph y = 1/x between x = 104 and x = 105 + ... + the area underneath the graph y = 1/x between x = 199 and x = 200).
For any given integer K, the "box" between x = K and x = K + 1 contains all of the points underneath the curve y = 1/x between K and K + 1, as well as the points above the curve and below y = 1/K, so the box's area > the integral section's area. This means the sum > the integral.

You are a mathematician who works for a game show.
A wheel of choice is marked with the numbers 1,2,...,n, and a prize is associated with each number.
A player faced with the wheel chooses some number q and starts spinning the wheel k times. On each spin, the wheel moves forward q steps in a clockwise direction and the number / prize reached is eliminated from the wheel (i.e., the player does not get it). After k such spins, all the prizes remaining on the wheel are gifted to the player.
At the beginning, the wheel's arrow points between 1 and n. If the wheel reaches the number t, t is removed from the wheel, the size of the remaining numbers are readjusted and evenly spaced, and the arrow is moved to the point in between t's left and right neighbors. Each step moves the wheel a little less than one number forward (so the wheel comes to rest on a number and not between two). So, if the wheel is right before 1 and performs 3 steps, it ends up on 3.
An example of the wheel for n=8:
:strip_icc()/pic6216946.png)
And after three spins with q=5:
:strip_icc()/pic6216947.png)
For a given n, we call a set of k numbers unwinnable if no matter what q the player chooses, he will not be able to win exactly this set after n-k spins. The game show wants to know the unwinnable sets of a given n to avoid handing out the best prizes.
For example, there are no unwinnable sets for n smaller than 9. For n=9, there are three unwinnable sets, all of size k=5:
(1, 2, 5, 8, 9)
(2, 3, 4, 5, 8)
(2, 5, 6, 7, 8)
Your goal: Find an n such that there is a set of unwinnable numbers for seven steps (i.e., the set is of size n-7). In your answer, supply the number n and the elements of the unwinnable set.


