Easy math puzzles
Poll
 | 21 votes (45.65%) | ||
| | 14 votes (30.43%) | ||
| | 6 votes (13.04%) | ||
| | 3 votes (6.52%) | ||
| | 12 votes (26.08%) | ||
| | 3 votes (6.52%) | ||
| | 6 votes (13.04%) | ||
| | 5 votes (10.86%) | ||
| | 12 votes (26.08%) | ||
| | 10 votes (21.73%) |
46 members have voted
May 17th, 2021 at 5:26:38 PM
permalink
Quote: Ace2Round 1: don’t switch
Round 2: either
Round 3: switch
Correct!!!
Quote: EdCollinsIf I was on stage, and had to make a decision right then and there, I would NOT switch initially, and hope I did not pick the right door, hoping to win in Round 2 or Round 3.
And given the opportunity, assuming if I did indeed not pick the right door in Round 1, and thus now advanced to the special zonk Second Round, at that point I think I would switch doors.
If I did not guess right here either, and thus advanced to the 3rd round, I'd definitely switch of course, hoping for the best shot at that final prize of $30,000.
I suspect it's right not to switch in Round 1 and of course you always switch in Round 3. The one round I'm least confident in is the Second Round, but yea, let's switch here too, for the best chance at the $20,000.
Although indecisive about round 2, this response is technically Correct!
As mentioned, everything keys off of round 3 where, assuming you reach it, you should always switch. This simplifies things to 3 possibilities...
switch, switch, switch
stand, switch, switch
stand, stand, switch
The strategy is that if the cash amount for the next round is greater than 1.5 times the current cash amount, you should stand and hope to lose the round. If, however, the cash amount for the next round is less than 1.5 times the current amount, you should switch and hope to win the round. Since 20k is two times 10k, you should always try to lose the first round.
What about round 2? Since 30k is neither greater than nor less than but is rather exactly 1.5 times 20k, the potential return is the same for either choice. (Although I would personally follow the EdCollins strategy which intuitively feels like a wiser path. Lord, what fools these mortals be!)
switch, switch, switch
stand, switch, switch
stand, stand, switch
The strategy is that if the cash amount for the next round is greater than 1.5 times the current cash amount, you should stand and hope to lose the round. If, however, the cash amount for the next round is less than 1.5 times the current amount, you should switch and hope to win the round. Since 20k is two times 10k, you should always try to lose the first round.
What about round 2? Since 30k is neither greater than nor less than but is rather exactly 1.5 times 20k, the potential return is the same for either choice. (Although I would personally follow the EdCollins strategy which intuitively feels like a wiser path. Lord, what fools these mortals be!)
--------------------------------------------------------------
Have you tried 22 tonight? I said 22.
May 18th, 2021 at 2:35:25 PM
permalink
It's toughie Tuesday!
Let x<y
Q1. For what values of x is x^y > y^x?
Q2. For what values of y is x^y > y^x?
Q3: For what values of x and y does it depend on y-x?
Let x<y
Q1. For what values of x is x^y > y^x?
Q2. For what values of y is x^y > y^x?
Q3: For what values of x and y does it depend on y-x?
Last edited by: Wizard on May 18, 2021
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 18th, 2021 at 6:14:38 PM
permalink
Quote: WizardIt's toughie Tuesday!
Let x>y
Q1. For what values of x is x^y > y^x?
Q2. For what values of x is x^y < y^x?
Q3: For what values of x does it depend on x-y ?
For each question, is it asking for what values of x does the inequality hold over all positive y?
If it does, then...
the answer to Q1 is 0 < x <= e
To show this, first look at the function f(x) = ln x / x.
df/dx = (x * 1/x - ln x * 1) / x^2 = (1 - ln x) / x^2. This has one zero, at x = e.
d^f/dx^2 = (x^2 * (-1/x) - (1 - ln x) * 2x) / x^4 = (-x - 2x + 2x ln x) / x^4 = (2x ln x - 3x) / x^4. At x = e, this is (2e - 3e) / e^4 < 0, so f(x) is a maximum at x = e.
For all positive x <> e, ln x / x < ln e / e -> e^(ln x / x) < e^(ln e / e) (since e^x is strictly increasing) -> x^(1/x) < e^(1/e) -> (x^(1/x))^(ex) < (e^(1/e))^(ex) -> x^e < e^x.
If 0 < y < x <= e, then x^y > y^x.
However, if x > e, then let y = e; you get x^e > e^x, which is not true.
I want to say that the answer to Q2 is none.
For any x > 1, let y = 1; x^1 > 1^x
For all x <= 1, since y < x < e, x^y > y^x.
May 18th, 2021 at 6:20:44 PM
permalink
Quote: ThatDonGuyFor each question, is it asking for what values of x does the inequality hold over all positive y?
I didn't state the questions properly, but based on your answer, you get what I was trying to ask.
This was a tough one, so please add one more beer I owe you to my tab.
I edited the OP to ask the question properly, hopefully.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 18th, 2021 at 6:33:48 PM
permalink
The way you have them written now, 1 and 2 are the same question. Should the sign in #2 be facing the other way?
May 18th, 2021 at 6:37:42 PM
permalink
This is for x>y.
The answer to Q1 is 0<y<e. For example, 0.5^0.4>0.4^0.5; 2^1.5>1.5^2; and 3^2>2^3, but 4^2=2^4
The answer to Q2 is y>e. For example 4^3<3^4.
I don't understand Q3.
The answer to Q1 is 0<y<e. For example, 0.5^0.4>0.4^0.5; 2^1.5>1.5^2; and 3^2>2^3, but 4^2=2^4
The answer to Q2 is y>e. For example 4^3<3^4.
I don't understand Q3.
Last edited by: aceside on May 18, 2021
May 18th, 2021 at 6:53:15 PM
permalink
What’s e?
It’s all about making that GTA
May 19th, 2021 at 4:41:49 AM
permalink
This puzzle comes from the April/May 2021 Mensa Bulletin.
There are three seats in the logic room -- the High Seat, the Middle Seat, and the Low Seat. Each one is occupied by a different woman -- Alice, Betty, or Carol.
The woman in the High Seat always speaks truthfully.
The woman in the Middle Seat can speak truthfully or falsely as she chooses.
The woman in the Low Seat always speaks falsely.
Alice says, "Betty sits in the High Seat."
Betty said, "Carol sits in the Low Seat."
Carol says, "Alice sits in the Middle Seat."
Who sits in each seat?
There are three seats in the logic room -- the High Seat, the Middle Seat, and the Low Seat. Each one is occupied by a different woman -- Alice, Betty, or Carol.
The woman in the High Seat always speaks truthfully.
The woman in the Middle Seat can speak truthfully or falsely as she chooses.
The woman in the Low Seat always speaks falsely.
Alice says, "Betty sits in the High Seat."
Betty said, "Carol sits in the Low Seat."
Carol says, "Alice sits in the Middle Seat."
Who sits in each seat?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 19th, 2021 at 5:32:22 AM
permalink
Quote: WizardThis puzzle comes from the April/May 2021 Mensa Bulletin.
There are three seats in the logic room -- the High Seat, the Middle Seat, and the Low Seat. Each one is occupied by a different woman -- Alice, Betty, or Carol.
The woman in the High Seat always speaks truthfully.
The woman in the Middle Seat can speak truthfully or falsely as she chooses.
The woman in the Low Seat always speaks falsely.
Alice says, "Betty sits in the High Seat."
Betty said, "Carol sits in the Low Seat."
Carol says, "Alice sits in the Middle Seat."
Who sits in each seat?
Alice cannot sit in the high seat.
If she were sitting in the low seat, Betty also cannot sit in the high seat, since Alice's statement would be a lie. Which means it must go CBA from high to low. But that means Carol's statement would be a lie, so that cannot be true.
That means Alice sits in the middle seat, Carol's statement means she must sit in the high seat and not the low seat. Which means Betty sits in the low seat..
May 19th, 2021 at 7:02:32 AM
permalink
Quote: TomG
Alice cannot sit in the high seat.
If she were sitting in the low seat, Betty also cannot sit in the high seat, since Alice's statement would be a lie. Which means it must go CBA from high to low. But that means Carol's statement would be a lie, so that cannot be true.
That means Alice sits in the middle seat, Carol's statement means she must sit in the high seat and not the low seat. Which means Betty sits in the low seat..
I agree!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 19th, 2021 at 11:57:37 AM
permalink
Quote: Ace2What’s e?
The note between D and F. In the C Major scale, it's "Mi" (as in Do, Re, Mi, Fa...)
Seriously, it's the number where, if you graph y = e^x, the slope of the graph at x is y. It is the base of "natural" logarithms (the function "ln" is the base-e logarithm; that is, if e^x = y, then ln y = x). Its value is 1 + 1 / 1! + 1 / 2! + 1 / 3! + ... = about 2.7182818.
May 19th, 2021 at 12:22:12 PM
permalink
Those that did mainframe and hexadecimal might remember there was Able, Baker, Charlie, Dog, Easy and Fox. Perhaps that's why they're called "Easy" Maths puzzles as it's all about e.
I'm not sure how they got to this combination of the NATO alphabet, but can see the same list at https://arstechnica.com/civis/viewtopic.php?f=23&t=508410 and https://community.ibm.com/community/user/ibmz-and-linuxone/blogs/destination-z1/2019/12/23/first-encounters-of-the-z-kind .
I'm not sure how they got to this combination of the NATO alphabet, but can see the same list at https://arstechnica.com/civis/viewtopic.php?f=23&t=508410 and https://community.ibm.com/community/user/ibmz-and-linuxone/blogs/destination-z1/2019/12/23/first-encounters-of-the-z-kind .
May 19th, 2021 at 1:36:52 PM
permalink
Quote: ThatDonGuyThe note between D and F. In the C Major scale, it's "Mi" (as in Do, Re, Mi, Fa...)
Seriously, it's the number where, if you graph y = e^x, the slope of the graph at x is y. It is the base of "natural" logarithms (the function "ln" is the base-e logarithm; that is, if e^x = y, then ln y = x). Its value is 1 + 1 / 1! + 1 / 2! + 1 / 3! + ... = about 2.7182818.
Was he serious? I thought a joke. He’s constantly doing Poisson distributions and integrals with an e in it.
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
May 19th, 2021 at 1:56:43 PM
permalink
Quote: unJonWas he serious? I thought a joke. He’s constantly doing Poisson distributions and integrals with an e in it.
I thought he was joking too.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 20th, 2021 at 8:00:23 AM
permalink
MrCasinoGames starts messing around with his 20-sided (icosahedron) dice. He selects three of them (each numbered 1-20) and decides to make a casino game with an in-between theme.
His first idea is to have the house roll two of the dice and the player roll the third. If the player rolls a number on his die between the two numbers the house rolled, then the player wins. Otherwise, the house wins (including ties).
For his second idea, two of the 20-sided dice are rolled and the player gets to choose one of them for his in-between number. The third die is then rolled to determine the house's second number.
His third idea combines the first two. The player can either select one of the first two dice rolled as his number, or choose to roll the third die.
Assuming optimal choices, what is the probability the player will win the first game idea? The second game idea? The third game idea?
Have you tried 22 tonight? I said 22.
May 20th, 2021 at 8:22:23 AM
permalink
The geometry of icosahedron is a math of itself. This is complicated.
May 20th, 2021 at 9:15:23 AM
permalink
Yes, it was nerd humorQuote: WizardI thought he was joking too.
It’s all about making that GTA
May 20th, 2021 at 12:18:05 PM
permalink
Interestingly, thanks to Stephen, I have a few of his dice and they actually have 0 00 1-18!Quote: Gialmere...Assuming optimal choices, what is the probability the player will win the first game idea? The second game idea? The third game idea?
If there were an infinite number of numbers then the chances would be 1/3. The logic is pick the three numbers, the chances you have the middle one is 1 in 3.
Assume the lower die roll is X and the higher one is Y. With the an icosahedron your chances are (Y-X-2) or zero if Y-X is 1 or 0.
With the second game you get to choose the largest range of [1 to (X-1)], [(X+1) to (Y-1)] or [(Y+1) to 20] as winners. I'm sure someone with a good knowledge of integration can work this out for infinite numbers, looks like it's 1/2!
Using a spreadsheet I get your chances of winning as (i) 28.50% (ii) 43.875% (iii) 54.15%; so a reasonable game would be having to bet both (ii) and (iii).
Interestingly with larger numbers the second game gets very interesting - I sense a possible online game is there!
For 100-sided it is 32.34% 48.755% 59.6994%
For 1k - sided it is 33.233% 49.875% 60.969%
Actually for all the dice here the game two with a win if the two rolls were equal makes for a great game!
Also for normal dice, consider this easy game.
(i) If the rolls are the same - WIN
(ii) Else you have to roll either between the two dice - WIN
(iii) Roll equal to either of the two dice - STANDOFF (I did have roll the higher to win, but it's the same payback using this method).
(c) Charlie Patrick !!
Win 76, Tie 60, Lose 80.
Assume the lower die roll is X and the higher one is Y. With the an icosahedron your chances are (Y-X-2) or zero if Y-X is 1 or 0.
With the second game you get to choose the largest range of [1 to (X-1)], [(X+1) to (Y-1)] or [(Y+1) to 20] as winners. I'm sure someone with a good knowledge of integration can work this out for infinite numbers, looks like it's 1/2!
Using a spreadsheet I get your chances of winning as (i) 28.50% (ii) 43.875% (iii) 54.15%; so a reasonable game would be having to bet both (ii) and (iii).
Interestingly with larger numbers the second game gets very interesting - I sense a possible online game is there!
For 100-sided it is 32.34% 48.755% 59.6994%
For 1k - sided it is 33.233% 49.875% 60.969%
Actually for all the dice here the game two with a win if the two rolls were equal makes for a great game!
Also for normal dice, consider this easy game.
(i) If the rolls are the same - WIN
(ii) Else you have to roll either between the two dice - WIN
(iii) Roll equal to either of the two dice - STANDOFF (I did have roll the higher to win, but it's the same payback using this method).
(c) Charlie Patrick !!
Win 76, Tie 60, Lose 80.
May 20th, 2021 at 5:24:51 PM
permalink
Quote: charliepatrickInterestingly, thanks to Stephen, I have a few of his dice and they actually have 0 00 1-18!
If there were an infinite number of numbers then the chances would be 1/3. The logic is pick the three numbers, the chances you have the middle one is 1 in 3.
Assume the lower die roll is X and the higher one is Y. With the an icosahedron your chances are (Y-X-2) or zero if Y-X is 1 or 0.
With the second game you get to choose the largest range of [1 to (X-1)], [(X+1) to (Y-1)] or [(Y+1) to 20] as winners. I'm sure someone with a good knowledge of integration can work this out for infinite numbers, looks like it's 1/2!
Using a spreadsheet I get your chances of winning as (i) 28.50% (ii) 43.875% (iii) 54.15%; so a reasonable game would be having to bet both (ii) and (iii).
Interestingly with larger numbers the second game gets very interesting - I sense a possible online game is there!
For 100-sided it is 32.34% 48.755% 59.6994%
For 1k - sided it is 33.233% 49.875% 60.969%
Actually for all the dice here the game two with a win if the two rolls were equal makes for a great game!
Also for normal dice, consider this easy game.
(i) If the rolls are the same - WIN
(ii) Else you have to roll either between the two dice - WIN
(iii) Roll equal to either of the two dice - STANDOFF (I did have roll the higher to win, but it's the same payback using this method).
(c) Charlie Patrick !!
Win 76, Tie 60, Lose 80.
Correct!!
Very good.
Heh, yeah. I had to intentionally specify how they were numbered so as not to confuse those who might actually be familiar with his Roulette 18 dice. And what do you know -- my paranoia was justified.
----------------------------------------
Have you tried 22 tonight? I said 22.
May 20th, 2021 at 6:12:04 PM
permalink
So using 1,000 sided dice the answer for game 3 is 60.969%. What’s the limit as the number of sides trends towards infinity? I haven’t worked on this problem but my wild guesses (if 60.969 % is approaching the limit) would be: 1 - 1/e, the golden ratio minus 1, or the natural log of 2.
Last edited by: Ace2 on May 20, 2021
It’s all about making that GTA
May 24th, 2021 at 8:04:36 AM
permalink
It's easy monday. Let's play cards...
Place 2 Aces, 2 Kings, 2 Queens, and 2 Jacks in the spaces below so that:
Every Ace borders a King.
Every King borders a Queen.
Every Queen borders a Jack.
No two of the same cards border each other.
No Ace borders a Queen.
(Border means horizontal or vertical.)
:strip_icc()/pic6187469.png)
Place 2 Aces, 2 Kings, 2 Queens, and 2 Jacks in the spaces below so that:
Every Ace borders a King.
Every King borders a Queen.
Every Queen borders a Jack.
No two of the same cards border each other.
No Ace borders a Queen.
(Border means horizontal or vertical.)
Have you tried 22 tonight? I said 22.
May 24th, 2021 at 9:03:41 AM
permalink
[SPOILER=I'm not sure if these two are the only answers]
--K-
QJQ-
-AKJ
--A-
--K-
QJQ-
-AKA-
--J-
May 24th, 2021 at 6:00:26 PM
permalink
Quote: charliepatrick[SPOILE"=I'm not sure if these two are the only answers]
--K-
QJQ-
-AKJ
--A-
--K-
QJQ-
-AKA-
--J-
Correct!!...
(...heh, although you might want to brush up on your coding.)
-------------------------------------------
Have you tried 22 tonight? I said 22.
May 24th, 2021 at 11:40:03 PM
permalink
Sorry - I had lots to do yesterday so forgot to check it - also it doesn't allow me to edit it now!Quote: Gialmere......heh, although you might want to brush up on your coding.
May 25th, 2021 at 7:29:37 AM
permalink
I get the same answer as Gialmere, using brute force computing
May 25th, 2021 at 7:30:35 AM
permalink
It's toughie Tuesday. Let's play more cards...
Take a full suit of 13 cards. Each card weighs as many ounces as its value. Aces weigh 1 ounce, Jacks weigh 11, Queens weigh 12, and Kings weigh 13 ounces.
Take four bars of length 4 inches and create a mobile with the cards. You can tie to each bar in 5 places (at locations 0, 1, 2, 3, and 4 inches.) You can only tie once to each location.
On the lowest bar, tie 4 cards, and one string up to the next bar. On the other three bars, tie 3 cards, one string down to the previous bar, and one string up to the next. (The top bar has one string up to the ceiling.)
All bars balance. Assume the weight of the bars and strings are negligible.
Try to find solutions for which the center of mass is as high as possible and as low as possible.
Take a full suit of 13 cards. Each card weighs as many ounces as its value. Aces weigh 1 ounce, Jacks weigh 11, Queens weigh 12, and Kings weigh 13 ounces.
Take four bars of length 4 inches and create a mobile with the cards. You can tie to each bar in 5 places (at locations 0, 1, 2, 3, and 4 inches.) You can only tie once to each location.
On the lowest bar, tie 4 cards, and one string up to the next bar. On the other three bars, tie 3 cards, one string down to the previous bar, and one string up to the next. (The top bar has one string up to the ceiling.)
All bars balance. Assume the weight of the bars and strings are negligible.
Try to find solutions for which the center of mass is as high as possible and as low as possible.
Have you tried 22 tonight? I said 22.
May 26th, 2021 at 12:16:53 PM
permalink
Yes. The instructions could have been written better. Let me clarify...
As mentioned, strings and bars have no weight, nor does string length matter.
Obviously, to balance a bar you need equal weight on either side of its up-string. A card hung next to the up-string is 1x its weight. A card 2 spots away is 2x its weight. 3 spots equals 3x. For example...
Q-6-U-D-2
The 12oz queen is 2 spots away from the up-string and therefore doubles to 24oz. (If it was 3 spaces away, it would triple to 36oz.) The 6, being 1 space away from up, stays at 6oz for a total of 30oz.
On the other side, the deuce doubles to 4oz so the down-string must carry 26oz. Note that all cards hung on bars beneath this one are merely 1x their weight from this bar"s perspective. If, however, the 2 and D were reversed, then the deuce would be 2oz and the D would only need to carry (a now doubled) 14oz.
It's actually a fun type of puzzle (although perhaps I'm the only one to think so).
As mentioned, strings and bars have no weight, nor does string length matter.
Obviously, to balance a bar you need equal weight on either side of its up-string. A card hung next to the up-string is 1x its weight. A card 2 spots away is 2x its weight. 3 spots equals 3x. For example...
Q-6-U-D-2
The 12oz queen is 2 spots away from the up-string and therefore doubles to 24oz. (If it was 3 spaces away, it would triple to 36oz.) The 6, being 1 space away from up, stays at 6oz for a total of 30oz.
On the other side, the deuce doubles to 4oz so the down-string must carry 26oz. Note that all cards hung on bars beneath this one are merely 1x their weight from this bar"s perspective. If, however, the 2 and D were reversed, then the deuce would be 2oz and the D would only need to carry (a now doubled) 14oz.
It's actually a fun type of puzzle (although perhaps I'm the only one to think so).
Have you tried 22 tonight? I said 22.
May 26th, 2021 at 8:07:58 PM
permalink
Quote: Gialmere
Obviously, to balance a bar you need equal weight on either side of its up-string.
This statement is incorrect. To balance a bar, you need equal moment on either side of it’s up-string...
The rest are details...
May 27th, 2021 at 8:03:12 AM
permalink
I found 2 solutions where the center of mass is at its lowest, and 10 where it is at its highest
The two with the lowest Centers of Mass:
Down, Up, 6, 9, King
Down, Up, 4, 5, 10
Down, Up, 3, 2, 8
Queen, Ace, Up, Jack, 7
Down, Up, 3, Jack, King
Down, Up, 6, 4, 10
Down, Up, 5, 2, 7
Queen, Ace, Up, 9, 8
I get 132 total possible solutions, not including reflections
The two with the lowest Centers of Mass:
Down, Up, 6, 9, King
Down, Up, 4, 5, 10
Down, Up, 3, 2, 8
Queen, Ace, Up, Jack, 7
Down, Up, 3, Jack, King
Down, Up, 6, 4, 10
Down, Up, 5, 2, 7
Queen, Ace, Up, 9, 8
I get 132 total possible solutions, not including reflections
May 27th, 2021 at 9:21:26 AM
permalink
Let me make sure I have my physics right. Black lines are strings and the blue line is a balanced rod. The blue numbers are distances and the red numbers are weights. Find x.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 27th, 2021 at 9:23:49 AM
permalink
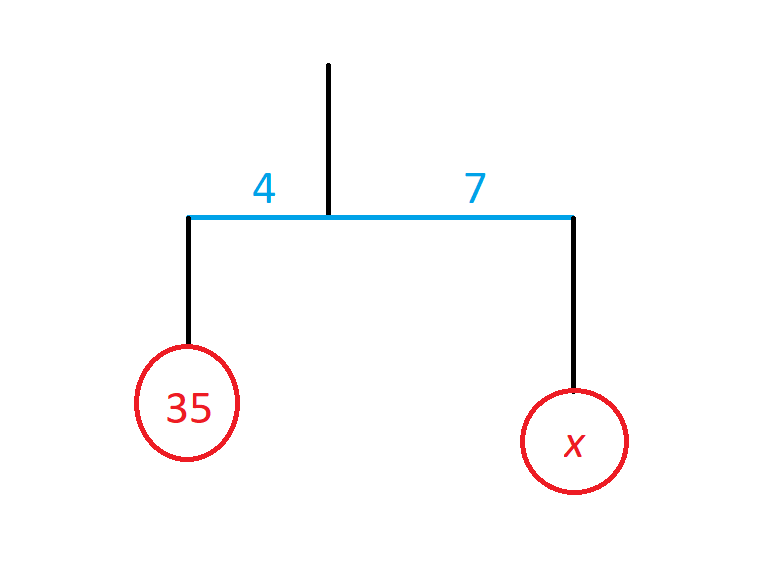
Quote: WizardLet me make sure I have my physics right. Black lines are strings and the blue line is a balanced rod. The blue numbers are distances and the red numbers are weights. Find x.
35 * 4^2 = X * 7^2
X = 560 / 49
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
May 27th, 2021 at 10:41:28 AM
permalink
Quote: ThatDonGuyI found 2 solutions where the center of mass is at its lowest, and 10 where it is at its highest
The two with the lowest Centers of Mass:
Down, Up, 6, 9, King
Down, Up, 4, 5, 10
Down, Up, 3, 2, 8
Queen, Ace, Up, Jack, 7
Down, Up, 3, Jack, King
Down, Up, 6, 4, 10
Down, Up, 5, 2, 7
Queen, Ace, Up, 9, 8
I get 132 total possible solutions, not including reflections
Can you also solve a simpler version of this problem?
Now consider 7 cards, and each card weighs as many ounces as its value: an ace weighs 1 ounce, a Two weighs 2 ounces, and so on, a Seven weighs 7 ounces.
Take 3 bars of length 3 inches and create a mobile with the cards. You can tie to each bar in 4 places (at locations 0, 1, 2, and 3 inches.) You can only tie once to each location.
May 27th, 2021 at 11:20:21 AM
permalink
Quote: acesideCan you also solve a simpler version of this problem?
Now consider 7 cards, and each card weighs as many ounces as its value: an ace weighs 1 ounce, a Two weighs 2 ounces, and so on, a Seven weighs 7 ounces.
Take 3 bars of length 3 inches and create a mobile with the cards. You can tie to each bar in 4 places (at locations 0, 1, 2, and 3 inches.) You can only tie once to each location.
I can't find any solutions to this. I will try it with different sets of seven cards.
I found one using Ace, 3, 5, 7, 9, Jack, King:
Down, Up, 5, King
Down, Up, Jack, 3
9, Up, 7, Ace
Last edited by: ThatDonGuy on May 27, 2021
May 27th, 2021 at 1:58:55 PM
permalink
Quote: unJonQuote: WizardLet me make sure I have my physics right. Black lines are strings and the blue line is a balanced rod. The blue numbers are distances and the red numbers are weights. Find x.
35 * 4^2 = X * 7^2
X = 560 / 49
Think seesaws (teeter-totters.)
A 35-kilogram kid at a distance of 4 units from the fulcrum can be balanced by a 20-kilogram kid 7 units from the fulcrum. (35)(4)=(20)(7)
May 27th, 2021 at 2:01:32 PM
permalink
Quote: ChesterDogQuote: unJonQuote: WizardLet me make sure I have my physics right. Black lines are strings and the blue line is a balanced rod. The blue numbers are distances and the red numbers are weights. Find x.
35 * 4^2 = X * 7^2
X = 560 / 49
Think seesaws (teeter-totters.)
A 35-kilogram kid at a distance of 4 units from the fulcrum can be balanced by a 20-kilogram kid 7 units from the fulcrum. (35)(4)=(20)(7)
Oh. I guess my physics is rusty. Thank you.
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
May 27th, 2021 at 2:15:41 PM
permalink
Quote: ThatDonGuyI can't find any solutions to this. I will try it with different sets of seven cards.
I found one using Ace, 3, 5, 7, 9, Jack, King:
Down, Up, 5, King
Down, Up, Jack, 3
9, Up, 7, Ace
I can't find any where the highest card is 7 or 8.
I found one where the highest card is 9:
Down, Up, 8, 7
Down, Up, 2, 6
9, Up, Ace, 4
There are 9 with the high card 10, 14 with the high card Jack, 26 with the high card Queen, and 43 with the high card King.
May 27th, 2021 at 4:22:46 PM
permalink
1-2-4-7-CCENTER- 6-5-3-blank
1*4+2*3+4*2+7*1 = 6*1+5*2+3*3 + 0*4
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
May 27th, 2021 at 4:22:49 PM
permalink
Sorry,inadvertent double post.
Or, maybe I'm just showing off.
1-2-4-7-CENTER- 6-5-3-blank
1*4+2*3+4*2+7*1 = 6*1+5*2+3*3 + 0*4
Or, maybe I'm just showing off.
1-2-4-7-CENTER- 6-5-3-blank
1*4+2*3+4*2+7*1 = 6*1+5*2+3*3 + 0*4
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
May 27th, 2021 at 5:16:36 PM
permalink
Quote: ThatDonGuyI found 2 solutions where the center of mass is at its lowest, and 10 where it is at its highest
The two with the lowest Centers of Mass:
Down, Up, 6, 9, King
Down, Up, 4, 5, 10
Down, Up, 3, 2, 8
Queen, Ace, Up, Jack, 7
Down, Up, 3, Jack, King
Down, Up, 6, 4, 10
Down, Up, 5, 2, 7
Queen, Ace, Up, 9, 8
I get 132 total possible solutions, not including reflections
Correct!
(Heh. At least I think.I lost track of things several posts ago.)
The best you can do is:
Center of mass is 57/182 above center.
Center of mass is 11/182 below center.
Here's a few examples...
:strip_icc()/pic6196692.png)
Center of mass is 57/182 above center.
Center of mass is 11/182 below center.
Here's a few examples...
---------------------------------------
Have you tried 22 tonight? I said 22.
May 27th, 2021 at 7:52:52 PM
permalink
Quote: gordonm888
1-2-4-7-CCENTER- 6-5-3-blank
1*4+2*3+4*2+7*1 = 6*1+5*2+3*3 + 0*4
This is very creative! This is the most original problem I have ever seen.
May 28th, 2021 at 7:38:18 AM
permalink
Meanwhile, at the satanic temple, worshipers gamble on a dice game called 666. The object is to create the highest three digit number possible.
A player rolls a fair die and decides which digit (100s, 10s, 1s) it will represent. The die is rolled again and the number is placed in one of the remaining two spots. A third roll is placed in the final empty spot.
What is the best strategy for this game and what is its expected value?
Have you tried 22 tonight? I said 22.
May 28th, 2021 at 8:19:21 AM
permalink
Playing around with this.
My first strategy (don't know if it's optimal yet) was:
If first roll is a 5 or 6, place in 100s spot. If first roll is a 1 or 2, place in the 1s spot. Else (dice roll of 3 or 4), place in 10s spot.
If second roll is 4, 5, 6 place in leftmost open spot. Else in right most open spot.
This gives an expected value of 504.
My first strategy (don't know if it's optimal yet) was:
If first roll is a 5 or 6, place in 100s spot. If first roll is a 1 or 2, place in the 1s spot. Else (dice roll of 3 or 4), place in 10s spot.
If second roll is 4, 5, 6 place in leftmost open spot. Else in right most open spot.
This gives an expected value of 504.
May 28th, 2021 at 8:41:47 AM
permalink
Quote: rsactuaryThis gives an expected value of 504.
I agree with the strategy, but I am getting an expected value of 498.5 (just slightly better than the 498.25 if a first roll of 3 is placed in the 1s spot).
May 28th, 2021 at 8:45:54 AM
permalink
Quote: ThatDonGuyI agree with the strategy, but I am getting an expected value of 498.5 (just slightly better than the 498.25 if a first roll of 3 is placed in the 1s spot).
Hmm.. if I have an error in my EV calc, I can't find it.
May 28th, 2021 at 8:55:49 AM
permalink
Quote: rsactuaryHmm.. if I have an error in my EV calc, I can't find it.
I did a simulation, and 504 does appear to be correct. I'll have to check my numbers again.
I see the problem: I was assigning the second die to the higher value on a 3-6 instead of a 4-6.
Now I get 504, and 503.625 for assigning a first die of 3 to 1 instead of 10.
Last edited by: ThatDonGuy on May 28, 2021
May 28th, 2021 at 9:19:52 AM
permalink
Agree - I did play around a bit more using a spreadsheet and your idea gives 504. Putting 3's into the Units Columns gives 503.625. Only keeping 6s is 492.75.Quote: rsactuaryPlaying around with this.
My first strategy (don't know if it's optimal yet) was:
If first roll is a 5 or 6, place in 100s spot. If first roll is a 1 or 2, place in the 1s spot. Else (dice roll of 3 or 4), place in 10s spot.
If second roll is 4, 5, 6 place in leftmost open spot. Else in right most open spot.
This gives an expected value of 504.
May 28th, 2021 at 10:11:42 AM
permalink
I've toyed a bit with a few tweaks to the strategy and can't come up with anything higher than 504. Assuming that this is optimal, I'm curious how one would go about proving it's optimal instead of relying on simulation.
May 28th, 2021 at 10:42:19 AM
permalink
^ I used a spreadsheet. Just create one with 216 rows ranging catering for 1 1 1, 1 1 2, ... 1 1 6, 1 2 1, ... 6 6 6. Look at the first digit and decide where it goes, look at the second digit and decide whether it goes in the earlier empty slot or later one, place the third digit in the empty slot.
There's only a few methods one can use but the obvious is for anything in a higher range place it in the 100s, for a middle range (if any) place it in the 10s, for a lower range place it in the 1s. There are only a few places where the border between these ranges can lie, so it's easy to try all the sensible ones out.
The second decision is obvious, since you want to maximise the expected value of the higher digit; so place any 3,2 or 1 in the lower of the two left.
Interestingly if you had a ten sided dice (numbered 1 to 10), then using the same spreadsheet method gives 1,2,3,4 go into the 1s, 5,6 into the 10s, and 7,8,9,10 into the 100s.
There's only a few methods one can use but the obvious is for anything in a higher range place it in the 100s, for a middle range (if any) place it in the 10s, for a lower range place it in the 1s. There are only a few places where the border between these ranges can lie, so it's easy to try all the sensible ones out.
The second decision is obvious, since you want to maximise the expected value of the higher digit; so place any 3,2 or 1 in the lower of the two left.
Interestingly if you had a ten sided dice (numbered 1 to 10), then using the same spreadsheet method gives 1,2,3,4 go into the 1s, 5,6 into the 10s, and 7,8,9,10 into the 100s.
May 28th, 2021 at 10:50:30 AM
permalink
Quote: gordonm888Sorry,inadvertent double post.
Or, maybe I'm just showing off.
1-2-4-7-CENTER- 6-5-3-blank
1*4+2*3+4*2+7*1 = 6*1+5*2+3*3 + 0*4
I find two more solutions for your problem:
7-6-5-HOOK-1-0-2-4-3
7*3+6*2+5*1=1*1+0*2+2*3+4*4+3*5;
And
7-6-1-HOOK-5-2-3-4-0
7*3+6*2+1*1=5*1+2*2+3*3+4*4+0*5.
Can anybody use your program to find all of the solutions?
May 28th, 2021 at 1:42:00 PM
permalink
Quote: acesideCan anybody use your program to find all of the solutions?
Could somebody point me to the post where this particular version of the problem is stated? I have a feeling it's a misinterpretation of the three-level one
2 7 6 / 5 4 3 1 0
3 5 6 / 7 4 2 1 0
3 5 7 / 4 6 2 1 0
3 5 7 / 6 2 4 1 0
3 6 5 / 7 4 1 2 0
3 6 5 / 7 4 2 0 1
3 6 7 / 2 5 4 1 0
3 6 7 / 4 2 5 0 1
3 6 7 / 4 5 0 1 2
3 6 7 / 5 2 1 4 0
3 7 4 / 5 6 2 1 0
3 7 4 / 6 5 1 2 0
3 7 4 / 6 5 2 0 1
3 7 5 / 6 1 4 2 0
3 7 5 / 6 4 0 1 2
3 7 6 / 2 4 5 1 0
3 7 6 / 2 5 4 0 1
3 7 6 / 4 1 5 2 0
3 7 6 / 5 1 2 4 0
3 7 6 / 5 1 4 0 2
4 5 6 / 3 7 1 2 0
4 5 6 / 3 7 2 0 1
4 5 6 / 7 1 3 0 2
4 5 6 / 7 2 0 3 1
4 5 7 / 2 6 1 3 0
4 5 7 / 3 2 6 1 0
4 5 7 / 3 6 0 1 2
4 5 7 / 6 0 2 3 1
4 5 7 / 6 0 3 1 2
4 5 7 / 6 1 2 0 3
4 5 7 / 6 2 0 1 3
4 6 3 / 7 5 2 1 0
4 6 5 / 2 7 3 1 0
4 6 5 / 7 0 3 2 1
4 6 5 / 7 2 1 0 3
4 6 7 / 2 1 5 3 0
4 6 7 / 2 3 1 5 0
4 6 7 / 2 5 0 1 3
4 6 7 / 3 0 5 2 1
4 6 7 / 3 1 2 5 0
4 6 7 / 5 0 1 2 3
4 7 3 / 6 2 5 1 0
4 7 3 / 6 5 0 2 1
4 7 3 / 6 5 1 0 2
4 7 5 / 1 6 2 3 0
4 7 5 / 2 3 6 0 1
4 7 5 / 2 6 0 3 1
4 7 5 / 3 1 6 2 0
4 7 5 / 6 0 1 3 2
4 7 5 / 6 0 2 1 3
4 7 5 / 6 1 0 2 3
4 7 6 / 0 5 3 2 1
4 7 6 / 1 2 5 3 0
4 7 6 / 1 3 5 0 2
4 7 6 / 1 5 2 0 3
4 7 6 / 3 0 5 1 2
4 7 6 / 3 2 0 5 1
5 3 6 / 7 2 4 1 0
5 3 7 / 6 1 4 2 0
5 3 7 / 6 4 0 1 2
5 4 6 / 2 7 3 1 0
5 4 6 / 7 0 3 2 1
5 4 6 / 7 2 1 0 3
5 4 7 / 1 6 3 2 0
5 4 7 / 2 3 6 1 0
5 4 7 / 3 2 6 0 1
5 4 7 / 6 1 0 3 2
5 6 2 / 7 3 4 1 0
5 6 2 / 7 4 3 0 1
5 6 3 / 7 2 1 4 0
5 6 4 / 2 7 1 3 0
5 6 4 / 3 7 0 1 2
5 6 4 / 7 1 0 3 2
5 6 7 / 0 2 3 4 1
5 6 7 / 0 4 1 2 3
5 6 7 / 1 2 3 0 4
5 6 7 / 3 0 1 2 4
5 7 2 / 3 6 4 1 0
5 7 2 / 4 6 1 3 0
5 7 2 / 6 3 1 4 0
5 7 2 / 6 4 0 3 1
5 7 3 / 2 4 6 1 0
5 7 3 / 4 1 6 2 0
5 7 3 / 6 0 4 1 2
5 7 4 / 1 3 6 2 0
5 7 4 / 2 6 0 1 3
5 7 4 / 3 1 6 0 2
5 7 6 / 0 2 4 1 3
5 7 6 / 0 3 1 4 2
5 7 6 / 1 0 4 3 2
5 7 6 / 1 3 0 2 4
5 7 6 / 2 0 3 1 4
5 7 6 / 2 1 0 4 3
6 2 7 / 3 5 4 1 0
6 2 7 / 4 3 5 1 0
6 2 7 / 4 5 1 3 0
6 3 4 / 7 5 1 2 0
6 3 4 / 7 5 2 0 1
6 3 5 / 4 7 1 2 0
6 3 5 / 4 7 2 0 1
6 3 5 / 7 1 4 2 0
6 3 5 / 7 4 0 1 2
6 3 7 / 1 5 4 2 0
6 3 7 / 2 5 1 4 0
6 3 7 / 4 1 5 0 2
6 3 7 / 4 2 1 5 0
6 3 7 / 5 0 4 1 2
6 4 3 / 5 7 2 1 0
6 4 5 / 2 7 1 3 0
6 4 5 / 3 7 0 1 2
6 4 5 / 7 1 0 3 2
6 4 7 / 0 5 2 3 1
6 4 7 / 0 5 3 1 2
6 4 7 / 1 3 2 5 0
6 4 7 / 1 5 0 3 2
6 4 7 / 2 1 3 5 0
6 4 7 / 2 3 0 5 1
6 5 2 / 7 3 4 0 1
6 5 2 / 7 4 1 3 0
6 5 3 / 4 7 0 2 1
6 5 3 / 4 7 1 0 2
6 5 3 / 7 1 2 4 0
6 5 3 / 7 1 4 0 2
6 5 4 / 1 7 3 2 0
6 5 4 / 3 2 7 1 0
6 5 4 / 7 0 1 3 2
6 5 4 / 7 0 2 1 3
6 5 4 / 7 1 0 2 3
6 5 7 / 0 2 4 1 3
6 5 7 / 0 3 1 4 2
6 5 7 / 1 0 4 3 2
6 5 7 / 1 3 0 2 4
6 5 7 / 2 0 3 1 4
6 5 7 / 2 1 0 4 3
6 7 1 / 3 5 4 2 0
6 7 1 / 4 3 5 2 0
6 7 1 / 4 5 3 0 2
6 7 1 / 5 2 4 3 0
6 7 1 / 5 3 2 4 0
6 7 1 / 5 3 4 0 2
6 7 2 / 3 4 1 5 0
6 7 2 / 3 5 0 4 1
6 7 2 / 5 0 4 3 1
6 7 2 / 5 1 4 0 3
6 7 2 / 5 3 1 0 4
6 7 3 / 0 5 4 2 1
6 7 3 / 1 4 2 5 0
6 7 3 / 2 1 5 4 0
6 7 3 / 2 4 0 5 1
6 7 3 / 2 5 1 0 4
6 7 3 / 4 0 2 5 1
6 7 3 / 5 0 2 1 4
6 7 3 / 5 1 0 2 4
6 7 4 / 0 2 5 3 1
6 7 4 / 0 5 1 2 3
6 7 4 / 2 0 3 5 1
6 7 4 / 2 0 5 1 3
6 7 4 / 2 3 1 0 5
6 7 4 / 3 0 1 5 2
6 7 4 / 3 1 2 0 5
6 7 4 / 3 2 0 1 5
6 7 5 / 0 1 3 4 2
6 7 5 / 0 1 4 2 3
6 7 5 / 0 2 3 1 4
6 7 5 / 0 3 1 2 4
6 7 5 / 1 2 0 3 4
6 7 5 / 2 0 1 3 4
7 2 4 / 6 5 3 1 0
7 2 5 / 4 6 3 0 1
7 2 6 / 3 4 5 0 1
7 2 6 / 4 5 0 3 1
7 2 6 / 5 1 4 3 0
7 2 6 / 5 4 1 0 3
7 3 4 / 5 2 6 1 0
7 3 4 / 5 6 0 1 2
7 3 4 / 6 1 5 2 0
7 3 5 / 2 4 6 1 0
7 3 5 / 4 1 6 2 0
7 3 5 / 6 0 4 1 2
7 3 6 / 1 5 2 4 0
7 3 6 / 1 5 4 0 2
7 3 6 / 2 4 1 5 0
7 3 6 / 2 5 0 4 1
7 3 6 / 4 0 5 1 2
7 3 6 / 4 2 0 5 1
7 3 6 / 5 1 0 4 2
7 3 6 / 5 1 2 0 4
7 3 6 / 5 2 0 1 4
7 4 2 / 5 6 3 0 1
7 4 2 / 6 3 5 1 0
7 4 2 / 6 5 1 3 0
7 4 3 / 5 2 6 0 1
7 4 5 / 0 6 3 2 1
7 4 5 / 1 6 2 0 3
7 4 5 / 2 1 6 3 0
7 4 5 / 3 0 6 2 1
7 4 5 / 3 2 1 6 0
7 4 6 / 0 3 5 1 2
7 4 6 / 0 5 1 3 2
7 4 6 / 0 5 2 1 3
7 4 6 / 1 2 5 0 3
7 4 6 / 3 1 0 5 2
7 4 6 / 3 2 1 0 5
7 5 1 / 6 3 4 2 0
7 5 1 / 6 4 2 3 0
7 5 2 / 3 4 6 1 0
7 5 2 / 4 3 6 0 1
7 5 2 / 4 6 0 3 1
7 5 2 / 6 1 3 4 0
7 5 2 / 6 3 0 4 1
7 5 2 / 6 4 0 1 3
7 5 3 / 4 1 6 0 2
7 5 3 / 6 1 0 4 2
7 5 3 / 6 1 2 0 4
7 5 3 / 6 2 0 1 4
7 5 4 / 0 6 2 3 1
7 5 4 / 0 6 3 1 2
7 5 4 / 1 2 6 3 0
7 5 4 / 1 3 6 0 2
7 5 4 / 1 6 0 3 2
7 5 4 / 2 3 1 6 0
7 5 4 / 3 0 6 1 2
7 5 4 / 3 1 2 6 0
7 5 6 / 0 1 3 4 2
7 5 6 / 0 1 4 2 3
7 5 6 / 0 2 3 1 4
7 5 6 / 0 3 1 2 4
7 5 6 / 1 2 0 3 4
7 5 6 / 2 0 1 3 4
7 6 1 / 3 4 5 2 0
7 6 1 / 5 2 3 4 0
7 6 1 / 5 4 2 0 3
7 6 2 / 1 5 4 3 0
7 6 2 / 4 1 3 5 0
7 6 2 / 4 3 0 5 1
7 6 2 / 5 0 3 4 1
7 6 2 / 5 3 0 1 4
7 6 3 / 0 4 5 2 1
7 6 3 / 0 5 4 1 2
7 6 3 / 1 2 5 4 0
7 6 3 / 2 1 4 5 0
7 6 3 / 2 5 0 1 4
7 6 3 / 4 1 0 5 2
7 6 3 / 4 2 1 0 5
7 6 3 / 5 0 1 2 4
7 6 4 / 0 3 2 5 1
7 6 4 / 1 3 0 5 2
7 6 4 / 2 3 0 1 5
7 6 5 / 0 2 1 4 3
7 6 5 / 1 0 2 4 3
7 6 5 / 1 0 3 2 4
0 2 7 6 / 5 4 3 1
0 3 5 6 / 7 4 2 1
0 3 5 7 / 4 6 2 1
0 3 5 7 / 6 2 4 1
0 3 6 5 / 7 4 1 2
0 3 6 7 / 2 5 4 1
0 3 6 7 / 5 2 1 4
0 3 7 4 / 5 6 2 1
0 3 7 4 / 6 5 1 2
0 3 7 5 / 6 1 4 2
0 3 7 6 / 2 4 5 1
0 3 7 6 / 4 1 5 2
0 3 7 6 / 5 1 2 4
0 4 5 6 / 3 7 1 2
0 4 5 7 / 2 6 1 3
0 4 5 7 / 3 2 6 1
0 4 6 3 / 7 5 2 1
0 4 6 5 / 2 7 3 1
0 4 6 7 / 2 1 5 3
0 4 6 7 / 2 3 1 5
0 4 6 7 / 3 1 2 5
0 4 7 3 / 6 2 5 1
0 4 7 5 / 1 6 2 3
0 4 7 5 / 3 1 6 2
0 4 7 6 / 1 2 5 3
0 5 3 6 / 7 2 4 1
0 5 3 7 / 6 1 4 2
0 5 4 6 / 2 7 3 1
0 5 4 7 / 1 6 3 2
0 5 4 7 / 2 3 6 1
0 5 6 2 / 7 3 4 1
0 5 6 3 / 7 2 1 4
0 5 6 4 / 2 7 1 3
0 5 7 2 / 3 6 4 1
0 5 7 2 / 4 6 1 3
0 5 7 2 / 6 3 1 4
0 5 7 3 / 2 4 6 1
0 5 7 3 / 4 1 6 2
0 5 7 4 / 1 3 6 2
0 6 2 7 / 3 5 4 1
0 6 2 7 / 4 3 5 1
0 6 2 7 / 4 5 1 3
0 6 3 4 / 7 5 1 2
0 6 3 5 / 4 7 1 2
0 6 3 5 / 7 1 4 2
0 6 3 7 / 1 5 4 2
0 6 3 7 / 2 5 1 4
0 6 3 7 / 4 2 1 5
0 6 4 3 / 5 7 2 1
0 6 4 5 / 2 7 1 3
0 6 4 7 / 1 3 2 5
0 6 4 7 / 2 1 3 5
0 6 5 2 / 7 4 1 3
0 6 5 3 / 7 1 2 4
0 6 5 4 / 1 7 3 2
0 6 5 4 / 3 2 7 1
0 6 7 1 / 3 5 4 2
0 6 7 1 / 4 3 5 2
0 6 7 1 / 5 2 4 3
0 6 7 1 / 5 3 2 4
0 6 7 2 / 3 4 1 5
0 6 7 3 / 1 4 2 5
0 6 7 3 / 2 1 5 4
0 7 2 4 / 6 5 3 1
0 7 2 6 / 5 1 4 3
0 7 3 4 / 5 2 6 1
0 7 3 4 / 6 1 5 2
0 7 3 5 / 2 4 6 1
0 7 3 5 / 4 1 6 2
0 7 3 6 / 1 5 2 4
0 7 3 6 / 2 4 1 5
0 7 4 2 / 6 3 5 1
0 7 4 2 / 6 5 1 3
0 7 4 5 / 2 1 6 3
0 7 4 5 / 3 2 1 6
0 7 5 1 / 6 3 4 2
0 7 5 1 / 6 4 2 3
0 7 5 2 / 3 4 6 1
0 7 5 2 / 6 1 3 4
0 7 5 4 / 1 2 6 3
0 7 5 4 / 2 3 1 6
0 7 5 4 / 3 1 2 6
0 7 6 1 / 3 4 5 2
0 7 6 1 / 5 2 3 4
0 7 6 2 / 1 5 4 3
0 7 6 2 / 4 1 3 5
0 7 6 3 / 1 2 5 4
0 7 6 3 / 2 1 4 5
1 2 6 5 / 7 4 0 3
1 2 6 7 / 3 5 0 4
1 2 6 7 / 5 0 4 3
1 2 7 4 / 6 5 0 3
1 2 7 6 / 4 3 0 5
1 2 7 6 / 5 0 3 4
1 3 4 6 / 5 7 0 2
1 3 5 4 / 7 6 0 2
1 3 5 6 / 7 0 2 4
1 3 5 7 / 2 6 0 4
1 3 5 7 / 4 0 6 2
1 3 6 7 / 0 5 2 4
1 3 7 4 / 5 0 6 2
1 3 7 5 / 0 6 4 2
1 3 7 5 / 4 2 0 6
1 3 7 6 / 2 0 5 4
1 4 3 5 / 7 6 0 2
1 4 3 7 / 6 0 5 2
1 4 5 6 / 0 7 2 3
1 4 5 6 / 3 0 7 2
1 4 5 7 / 3 0 2 6
1 4 6 3 / 7 2 0 5
1 4 7 2 / 6 3 0 5
1 4 7 3 / 5 2 0 6
1 4 7 5 / 2 0 3 6
1 5 2 6 / 7 3 0 4
1 5 2 7 / 6 0 4 3
1 5 3 7 / 0 6 4 2
1 5 3 7 / 4 2 0 6
1 5 4 7 / 0 2 6 3
1 5 6 2 / 3 7 0 4
1 5 6 3 / 0 7 4 2
1 5 6 4 / 0 3 7 2
1 5 6 4 / 2 0 7 3
1 5 6 4 / 3 2 0 7
1 5 7 0 / 4 6 3 2
1 5 7 2 / 3 4 0 6
1 5 7 3 / 2 0 6 4
1 5 7 4 / 0 2 3 6
1 6 2 5 / 7 0 4 3
1 6 2 7 / 4 0 3 5
1 6 3 5 / 4 0 7 2
1 6 3 7 / 0 2 5 4
1 6 4 3 / 7 0 2 5
1 6 4 5 / 0 3 7 2
1 6 4 5 / 2 0 7 3
1 6 4 5 / 3 2 0 7
1 6 5 0 / 7 4 3 2
1 6 5 4 / 2 3 0 7
1 6 7 0 / 2 5 4 3
1 6 7 0 / 4 3 2 5
1 6 7 2 / 0 3 4 5
1 7 0 6 / 4 5 3 2
1 7 0 6 / 5 3 4 2
1 7 0 6 / 5 4 2 3
1 7 2 3 / 6 5 0 4
1 7 2 4 / 6 0 5 3
1 7 2 5 / 4 0 6 3
1 7 2 5 / 4 3 0 6
1 7 2 6 / 0 4 5 3
1 7 2 6 / 0 5 3 4
1 7 2 6 / 3 0 4 5
1 7 3 2 / 5 6 0 4
1 7 3 4 / 0 6 5 2
1 7 3 4 / 5 0 2 6
1 7 3 5 / 2 0 6 4
1 7 4 0 / 6 5 3 2
1 7 4 2 / 3 6 0 5
1 7 4 2 / 5 0 6 3
1 7 4 2 / 5 3 0 6
1 7 4 2 / 6 0 3 5
1 7 4 3 / 0 5 6 2
1 7 4 3 / 2 5 0 6
1 7 5 0 / 3 6 4 2
1 7 5 0 / 6 2 3 4
1 7 5 2 / 0 6 3 4
1 7 5 2 / 3 0 6 4
1 7 5 2 / 4 0 3 6
1 7 5 3 / 0 2 6 4
1 7 5 3 / 0 4 2 6
1 7 5 3 / 2 0 4 6
1 7 6 0 / 2 4 5 3
1 7 6 0 / 2 5 3 4
1 7 6 0 / 3 4 2 5
1 7 6 0 / 4 2 3 5
2 0 7 6 / 5 4 1 3
2 1 5 6 / 7 4 0 3
2 1 5 7 / 4 6 0 3
2 1 5 7 / 6 3 0 4
2 1 6 7 / 4 3 0 5
2 1 6 7 / 5 0 3 4
2 1 7 4 / 5 6 0 3
2 1 7 5 / 6 0 4 3
2 1 7 6 / 3 4 0 5
2 1 7 6 / 4 0 5 3
2 3 4 7 / 5 0 1 6
2 3 5 6 / 0 7 1 4
2 3 6 5 / 4 1 0 7
2 3 7 1 / 6 5 0 4
2 3 7 4 / 0 6 1 5
2 3 7 4 / 1 5 0 6
2 3 7 5 / 0 1 6 4
2 4 1 7 / 5 6 0 3
2 4 3 7 / 1 6 0 5
2 4 5 1 / 7 6 0 3
2 4 5 3 / 7 1 0 6
2 4 6 0 / 7 5 1 3
2 4 6 1 / 7 3 0 5
2 4 6 3 / 1 7 0 5
2 4 6 3 / 5 1 0 7
2 4 6 5 / 0 3 1 7
2 4 7 1 / 3 6 0 5
2 4 7 1 / 5 0 6 3
2 4 7 1 / 5 3 0 6
2 4 7 1 / 6 0 3 5
2 4 7 3 / 0 5 1 6
2 5 1 6 / 7 0 4 3
2 5 3 4 / 7 1 0 6
2 5 3 6 / 4 0 1 7
2 5 3 7 / 0 1 6 4
2 5 4 1 / 6 7 0 3
2 5 4 3 / 7 0 1 6
2 5 4 6 / 0 3 1 7
2 5 6 3 / 1 0 7 4
2 5 6 4 / 0 1 3 7
2 5 7 0 / 1 6 4 3
2 5 7 0 / 4 3 1 6
2 5 7 1 / 0 4 6 3
2 6 0 7 / 4 1 5 3
2 6 0 7 / 4 3 1 5
2 6 1 5 / 3 7 0 4
2 6 1 7 / 0 4 5 3
2 6 1 7 / 0 5 3 4
2 6 1 7 / 3 0 4 5
2 6 3 1 / 7 5 0 4
2 6 3 4 / 5 0 1 7
2 6 3 5 / 1 4 0 7
2 6 4 0 / 5 7 1 3
2 6 4 3 / 0 7 1 5
2 6 4 5 / 0 1 3 7
2 6 5 0 / 3 7 1 4
2 6 5 1 / 4 0 7 3
2 6 5 3 / 0 1 7 4
2 6 5 3 / 0 4 1 7
2 7 0 5 / 3 6 1 4
2 7 0 6 / 1 5 4 3
2 7 0 6 / 4 1 3 5
2 7 1 3 / 6 4 0 5
2 7 1 4 / 3 6 0 5
2 7 1 4 / 5 0 6 3
2 7 1 4 / 5 3 0 6
2 7 1 4 / 6 0 3 5
2 7 1 5 / 0 6 4 3
2 7 1 6 / 0 3 5 4
2 7 1 6 / 0 4 3 5
2 7 3 0 / 6 5 1 4
2 7 3 1 / 4 6 0 5
2 7 3 4 / 1 0 6 5
2 7 4 0 / 5 1 6 3
2 7 4 0 / 6 1 3 5
2 7 4 1 / 5 0 3 6
2 7 4 3 / 0 1 6 5
2 7 4 3 / 1 0 5 6
2 7 5 0 / 1 4 6 3
2 7 5 0 / 3 1 6 4
2 7 5 0 / 4 1 3 6
2 7 5 1 / 0 3 6 4
3 0 5 7 / 6 2 1 4
3 0 6 7 / 2 5 1 4
3 0 6 7 / 4 2 1 5
3 0 7 6 / 4 1 2 5
3 1 4 7 / 6 2 0 5
3 1 5 7 / 4 2 0 6
3 1 6 4 / 7 2 0 5
3 1 6 5 / 2 7 0 4
3 1 6 7 / 0 4 2 5
3 1 6 7 / 2 0 4 5
3 1 7 4 / 5 2 0 6
3 1 7 5 / 0 6 2 4
3 1 7 5 / 2 4 0 6
3 1 7 5 / 4 0 2 6
3 1 7 6 / 0 2 5 4
3 2 4 7 / 1 6 0 5
3 2 5 6 / 4 1 0 7
3 2 5 7 / 0 4 1 6
3 2 5 7 / 1 0 6 4
3 2 6 5 / 4 0 1 7
3 2 7 1 / 5 6 0 4
3 2 7 5 / 1 0 4 6
3 4 1 7 / 5 2 0 6
3 4 2 5 / 7 1 0 6
3 4 2 7 / 0 6 1 5
3 4 2 7 / 1 5 0 6
3 4 5 1 / 7 2 0 6
3 4 5 2 / 6 1 0 7
3 4 6 1 / 5 2 0 7
3 4 7 2 / 0 1 6 5
3 4 7 2 / 1 0 5 6
3 5 1 7 / 2 0 6 4
3 5 2 6 / 1 4 0 7
3 5 2 7 / 0 1 4 6
3 5 4 2 / 6 0 1 7
3 5 6 0 / 4 2 1 7
3 5 6 2 / 1 0 4 7
3 5 7 0 / 1 2 4 6
3 6 0 4 / 7 2 1 5
3 6 0 5 / 2 7 1 4
3 6 0 7 / 1 2 4 5
3 6 1 4 / 2 7 0 5
3 6 2 1 / 5 7 0 4
3 6 2 1 / 7 4 0 5
3 6 2 5 / 0 1 7 4
3 6 2 5 / 0 4 1 7
3 6 4 1 / 5 0 2 7
3 6 5 0 / 4 1 2 7
3 6 5 1 / 0 2 7 4
3 6 5 2 / 0 1 4 7
3 7 0 2 / 6 5 1 4
3 7 0 4 / 2 6 1 5
3 7 0 4 / 5 1 2 6
3 7 0 5 / 2 1 6 4
3 7 1 2 / 5 4 0 6
3 7 1 2 / 6 0 5 4
3 7 1 5 / 0 2 4 6
3 7 2 0 / 6 4 1 5
3 7 2 1 / 4 5 0 6
3 7 2 1 / 6 0 4 5
3 7 2 4 / 0 1 5 6
3 7 4 0 / 1 5 2 6
3 7 4 1 / 0 2 6 5
4 0 7 3 / 6 2 1 5
4 0 7 5 / 2 3 1 6
4 0 7 5 / 3 1 2 6
4 1 3 6 / 7 2 0 5
4 1 3 7 / 6 0 2 5
4 1 5 6 / 3 2 0 7
4 1 5 7 / 0 3 2 6
4 1 6 2 / 7 3 0 5
4 1 6 5 / 2 3 0 7
4 1 7 2 / 3 6 0 5
4 1 7 2 / 5 3 0 6
4 1 7 2 / 6 0 3 5
4 1 7 3 / 2 5 0 6
4 2 3 5 / 7 1 0 6
4 2 3 7 / 0 6 1 5
4 2 3 7 / 1 5 0 6
4 2 5 6 / 1 0 3 7
4 2 6 3 / 0 7 1 5
4 2 6 5 / 0 1 3 7
4 2 7 1 / 3 5 0 6
4 2 7 3 / 1 0 6 5
4 3 1 6 / 7 0 2 5
4 3 1 7 / 2 6 0 5
4 3 2 5 / 7 0 1 6
4 3 2 6 / 1 7 0 5
4 3 2 6 / 5 1 0 7
4 3 5 2 / 6 0 1 7
4 3 6 2 / 1 5 0 7
4 3 7 0 / 1 6 2 5
4 3 7 0 / 2 5 1 6
4 3 7 1 / 0 5 2 6
4 3 7 1 / 2 0 6 5
4 3 7 2 / 0 1 5 6
4 5 0 7 / 1 2 3 6
4 5 1 6 / 2 0 3 7
4 5 3 1 / 6 2 0 7
4 5 3 2 / 1 7 0 6
4 6 0 2 / 7 3 1 5
4 6 0 5 / 2 3 1 7
4 6 0 5 / 3 1 2 7
4 6 1 3 / 5 0 2 7
4 6 1 5 / 0 2 3 7
4 6 2 0 / 7 1 3 5
4 6 2 1 / 5 3 0 7
4 6 2 3 / 0 5 1 7
4 6 3 0 / 5 2 1 7
4 6 3 2 / 1 0 7 5
4 7 0 1 / 6 3 2 5
4 7 1 0 / 6 2 3 5
4 7 1 2 / 0 6 3 5
4 7 1 2 / 3 0 6 5
4 7 1 3 / 0 2 6 5
4 7 2 1 / 3 0 5 6
4 7 3 0 / 1 2 6 5
4 7 3 0 / 2 1 5 6
5 0 4 7 / 2 3 1 6
5 0 4 7 / 3 1 2 6
5 0 7 3 / 2 4 1 6
5 0 7 4 / 1 2 3 6
5 1 2 7 / 4 3 0 6
5 1 4 6 / 3 0 2 7
5 1 6 3 / 2 4 0 7
5 1 6 3 / 4 0 2 7
5 1 6 4 / 2 0 3 7
5 1 7 2 / 3 0 4 6
5 1 7 3 / 0 2 4 6
5 2 1 7 / 3 4 0 6
5 2 3 4 / 6 1 0 7
5 2 4 3 / 6 0 1 7
5 2 6 1 / 3 4 0 7
5 2 6 3 / 1 0 4 7
5 2 7 1 / 0 4 3 6
5 3 0 7 / 4 1 2 6
5 3 1 4 / 7 2 0 6
5 3 1 7 / 0 4 2 6
5 3 1 7 / 2 0 4 6
5 3 2 4 / 6 0 1 7
5 3 2 6 / 0 4 1 7
5 3 4 1 / 6 2 0 7
5 3 4 2 / 1 7 0 6
5 3 6 0 / 2 4 1 7
5 3 6 1 / 0 4 2 7
5 3 6 1 / 2 0 4 7
5 4 0 6 / 3 2 1 7
5 4 1 3 / 7 0 2 6
5 4 1 6 / 0 3 2 7
5 4 2 1 / 7 3 0 6
5 4 2 3 / 1 7 0 6
5 4 3 0 / 7 2 1 6
5 6 0 3 / 2 4 1 7
5 6 0 4 / 1 2 3 7
5 6 2 0 / 3 4 1 7
5 6 2 1 / 3 0 4 7
5 6 3 0 / 2 1 4 7
5 7 0 2 / 1 3 4 6
5 7 1 0 / 2 4 3 6
5 7 1 0 / 3 2 4 6
6 0 5 4 / 3 2 1 7
6 1 3 4 / 5 2 0 7
6 1 3 5 / 2 4 0 7
6 1 3 5 / 4 0 2 7
6 1 4 5 / 0 3 2 7
6 1 5 2 / 3 4 0 7
6 1 5 4 / 0 2 3 7
6 2 3 5 / 1 0 4 7
6 2 4 1 / 5 3 0 7
6 2 4 3 / 0 5 1 7
6 2 5 1 / 4 0 3 7
6 3 1 4 / 5 0 2 7
6 3 2 4 / 0 5 1 7
6 3 2 5 / 0 1 4 7
6 3 4 0 / 5 1 2 7
6 3 5 0 / 1 4 2 7
6 3 5 1 / 0 2 4 7
6 4 0 5 / 1 3 2 7
6 4 0 5 / 2 1 3 7
6 4 2 1 / 3 5 0 7
6 4 3 2 / 1 0 5 7
6 5 0 2 / 4 3 1 7
6 5 1 2 / 3 0 4 7
6 5 1 3 / 0 2 4 7
6 5 2 0 / 4 1 3 7
6 5 3 0 / 1 2 4 7
