Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
DisagreeQuote: ThatDonGuy
I'll go with the obvious answer: I expect him to be on the sidewalk.
Since the sidewalk runs north-south, the distance from the sidewalk will be the difference between the number of steps east and the number of steps west. However, since these are equally likely with each step, the expected number of steps east equals the expected number of steps west.
For that matter, since the expected number of steps north equals the number of steps south, I expect him to be at his starting location.
link to original post
The answer is (10,000/π)^.5 =~ 56.419 steps from the sidewalk. Thatís technically an approximation though a very accurate one. The formula comes from integrating the normal curve times x from zero to infinity then multiplying times two. This gives the expected distance from the mean.Quote: Ace2Hereís another easy one:
A drunkard starts walking on a straight sidewalk that runs north-south. His goal is to walk northward, but for each step heís equally likely to go one foot directly north, south, east or west.
After 10,000 steps, how far off the sidewalk would you expect him to be?
Closed form solutions only.
link to original post
The exact answer (shown to ten digits) of 56.41825312 can be obtained via Markov chain, though thatís not a closed form solution.
If you were to start searching for the drunkard, the best place to start would be at the sidewalk since you donít know which side of it heís on, but youíd be an average of ~56 steps away from it when you found him. The chance of him being on the sidewalk is <1%
Quote: Ace2The answer is (10,000/π)^.5 =~ 56.419 steps from the sidewalk. Thatís technically an approximation though a very accurate one. The formula comes from integrating the normal curve times x from zero to infinity then multiplying times two. This gives the expected distance from the mean.
The exact answer (shown to ten digits) of 56.41825312 can be obtained via Markov chain, though thatís not a closed form solution.
link to original post
Technically, an approximation isn't one either.
The closest to a "closed form solution" that I got was this:
Each step has probability 1/4 of adding 1 to the number of steps to the left of the sidewalk, 1/4 of subtracting 1, and 1/2 of keeping it the same.
Let (m, n, 10,000 - (m + n)) represent the number of steps to the left, the number to the right, and the number forward/backward, with each one being >= 0 and <= 10,000.
The number of steps away from the sidewalk is |m - n|, and the probability of that particular triple is C(10,000, m) C(10,000 - m, n) (1/4)^10,000, or C(10,000, m) C(10,000 - m, n) / 2^20,000.
The solution is the sum over all m from 0 to 10,000 of (the sum over all n from 0 to (10,000 - n) of ( |m - n| C(10,000, m) C(10,000 - m, n) ) ), divided by 2^20,000.
However, I could not find a way to simplify that.
-62-36
Quote: WizardI get a lot of simple math problems on my Facebook feed. Usually there is a strong consensus on the answer, but this one is split about 50/50.
-62-36-72
link to original post
My answer would be:
- 6² - 36
= - (6 * 6)-36
= - 36 - 36
= - 72
An alternate solution using brackets is:
(-6 * -6) - 36
= 0
Quote: WizardI get a lot of simple math problems on my Facebook feed. Usually there is a strong consensus on the answer, but this one is split about 50/50.
-62-36-72
link to original post
Quote: WizardI get a lot of simple math problems on my Facebook feed. Usually there is a strong consensus on the answer, but this one is split about 50/50.
-62-36-72
link to original post
Wizard is correct
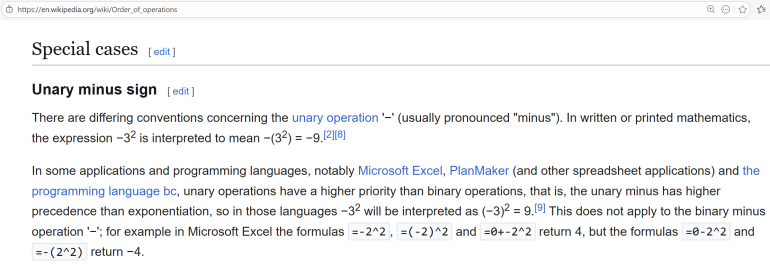
Thus, state the convention you are using to decide whether exponentiation or unary minus has precedence.
Dog Hand
(-6)^2 (-36) = -1,296
I donít agree with that answer but one could make the argument if parentheses can be implied
Quote: Ace2If parentheses are implied around the -6 to get (-6)^2 - 36 =0, then we should be consistent and assume parentheses are implied around the -36. Therefore:
(-6)^2 (-36) = -1,296
I donít agree with that answer but one could make the argument if parentheses can be implied
link to original post
Except that, since that minus sign is between two numbers, it is not unary, but binary.


