Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
There are only seven partitions of six using 1-3 digits:Quote: WizardHere is something a bit easier.
How many ways are there to put six distinct balls into three identical boxes?
Is there a general formula for n distinct balls into three identical boxes?
link to original post
6
15
24
33
114
123
222
It's easy to calculate the number of combinations for any of them. For instance, there are combin(6,1) * combin(5,2) * combin(3,3) = 60 combinations of 123. The combinations of all seven partitions sum to the answer of 122 combinations for boxes containing 0-6 balls.
If all boxes must contain at least one ball, then we subtract the 32 combinations of 6, 15, 24 and 33 to get the answer of 90 combinations
Incidentally, regarding the ďrandom board cutsĒ problem: You guys analyzed it for days, eventually concluding there was no direct solution for n cuts, then I post the direct solution using nothing but basic combinatorics/calculus, and apparently no one cares?
Quote: Ace2The combinations of all seven partitions sum to the answer of 122 combinations for boxes containing 0-6 balls.
I agree!
Sorry for the tardy response.
Quote:
Incidentally, regarding the ďrandom board cutsĒ problem: You guys analyzed it for days, eventually concluding there was no direct solution for n cuts, then I post the direct solution using nothing but basic combinatorics/calculus, and apparently no one cares?
link to original post
Sorry but I was out of town for almost a month and didn't see it. I'll have a look.
Quote: Ace2
Let's say you have 100 baseballs lined up on the ground and you randomly divide them into 5 groups (a group can contain 0-100 balls). There are combin(101,4) ways to insert 4 dividers among 101 positions to create the 5 groups. If you want to ensure all 5 groups contain at least 3 balls, then you remove 5*3 balls, then randomly insert 4 dividers into the remaining 85 balls ((combin(86,4) ways), then add 3 balls back to each group. Therefore, the probability that each of the 5 random groups contains at least 3 balls is 86*85*84*83/(101*100*99*98). As the total number of balls (n) goes to infinity, the probability that each group contains at least 0.03n balls is obviously 0.85^4. Therefore, as n goes to infinity, the probability that all 5 groups contain least xn balls is (1 - 5x)^4
So if we make 4 random cuts into a 1 foot long board, we know that the probability of all 5 pieces being at least x long is (1 - 5x)^4. Now we apply the very useful property that the expected value of an event to happen is the cumulative probability of it never happening. The "event" is finding a piece shorter than x. For this problem, this means: add the probabilities that all pieces are longer than x for all x from 0 to 0.20 (obviously all 5 pieces can't be longer than 0.20). We get this sum by integrating (1 - 5x)^4 dx from 0 to 0.20, which gives us the answer of 1/25 feet =expected length of shortest piece
Putting it all together, the expected length of the shortest piece when making (s - 1) cuts into a 1 foot board to get (s) pieces is the integral from 0 to 1/s of (1 - sx)^(s-1) dx, which evaluates to 1/s^2. So, for example, if we are cutting the board into s=8 pieces, the expected length of the shortest piece is 1/8^2
Note: the probability of all segments having a minimum size can be explained without the discrete baseball example as follows. But IMO, the discrete example is more intuitive. Starting with a board 1 foot long, you want to make 4 random cuts into 5 pieces with a minimum length of 0.03. You accomplish this by drawing a line at length 5 * 0.03 =0.15, then make the 4 random cuts irrespective of the line. If they all fall on the 0.85 side then subdivide the 0.15 side into 5 pieces of 0.03 and fasten one of them to each of the 5 pieces cut on the 0.85 side. So there's a (1-0.15)^4 chance they all fall on the 0.85 side and no pieces are <0.03
link to original post
This is really good. Thank you. I think I'll make an Ask the Wizard question out of it. Sorry it took so long to reply. I was out of town.
You take a 100 foot board, make one random cut and keep the shorter piece. Then you take another 100 foot board, make two random cuts and keep the shortest piece. Then you take another 100 foot board, make three random cuts and keep the shortest piece. This pattern continues forever.
What's the expected length of all the shortest pieces combined?
Quote: Ace2Now for a truly easy math puzzle.
You take a 100 foot board, make one random cut and keep the shorter piece. Then you take another 100 foot board, make two random cuts and keep the shortest piece. Then you take another 100 foot board, make three random cuts and keep the shortest piece. This pattern continues forever.
What's the expected length of all the shortest pieces combined?
link to original post
The expected length of cutting a 100-foot board into N pieces is 100 / N^2, so the sum is 100 / 2^2 + 100 / 3^2 + 100 / 4^2 + ...
= 100 (1 / 2^2 + 1 / 3^2 + 1 / 4^2 + ...)
= 100 ((1 + 1 / 2^2 + 1 / 3^2 + 1 / 4^2 + ...) - 1)
= 100 (PI^2 / 6 - 1)
= 50 PI^2 / 3 - 100, or about 64.4934.

Height = 2 + sqrt(24) / 3
Consider a tetrahedron with vertices (1,1,0), (1,0,1), (0,1,1), and (0,0,0).
The coordinates of the center of a face of the tetrahedron are the average of coordinates of its vertices. The average of (1,1,0), (1,0,1), and (0,1,1) is (2/3, 2/3, 2/3). The distance between this center and (0,0,0) is sqrt(4/9 + 4/9 + 4/9), which is sqrt(12) / 3.
Place a sphere at each vertex. Touching spheres would have radii of sqrt (2) / 2. The height of the group of spheres would be sqrt(12) / 3 + sqrt(2).
Scale the ball pyramid height such that the radii are 1 instead of sqrt (2) / 2. The objectís height would then be sqrt (24) / 3 + 2.
$40,000 in cash today or $40,000 financed over five years at 12% APR compounded CONTINUOUSLY. So there would be 5*12 = 60 equal payments (first payment due one month from today).
If you decide to finance, how much would the monthly payment be?
If the APR is 12%, then the amount the principle is multiplied by each time for monthly payments is 1.12^(1/12).
Let I = 1.12^(1/12), P = 50,000, and N = 60.
Applying the interest/loan formula P I^N = M (I^N - 1) / (I - 1), rewritten as M = P I^N (I - 1) / (I^N - 1), we get the monthly payment = $1096.79.
Of course, if it's me, I pay the $40,000 up front. I haven't made payments on a car since 1988.
Also, doesn't "APR" always mean that the interest is compounded continuously? A 12% annual rate, compounded monthly, has an APR of about 12.6825%.
Quote: Ace2If you decide to finance, how much would the monthly payment be?
link to original post
If the interest is 12% per year, then it's 1% per month, so it's .001% per 1/1000th month, etc.
As a comparison if 12% were applied each year and you never paid anything back, then on $40k after 5 years I get it you owe $70,493.67 (1.12^5*40k). Whereas the 1/1000th method gives it at 72,884.53.
APR means annual percentage rate. The compounding interval is another variable. A normal car/house loan is paid back monthly and also compounded monthly. So for a 12% APR, 12% / 12 months per year = 1% of interest is added to the outstanding balance every month. This would be an APY (annual percentage yield) of 1.01^12 - 1 =~ 12.68%. Compounded daily would be an APY of (1 + .12/365)^365 - 1 =~ 12.75%. For this problem, interest is compounded CONTINUOUSLY.Quote: ThatDonGuy
If the APR is 12%, then the amount the principle is multiplied by each time for monthly payments is 1.12^(1/12).
Let I = 1.12^(1/12), P = 50,000, and N = 60.
Applying the interest/loan formula P I^N = M (I^N - 1) / (I - 1), rewritten as M = P I^N (I - 1) / (I^N - 1), we get the monthly payment = $1096.79.
Of course, if it's me, I pay the $40,000 up front. I haven't made payments on a car since 1988.
Also, doesn't "APR" always mean that the interest is compounded continuously? A 12% annual rate, compounded monthly, has an APR of about 12.6825%.
link to original post
Your answer is for an APR of (1.12^(1/12) - 1) * 12 =~ 11.39% compounded MONTHLY for an APY of 12%, applied to a $50,000 loan instead of $40,000. Disagree
A few dollars off. DisagreeQuote: WizardQuote: Ace2If you decide to finance, how much would the monthly payment be?
link to original post$905.01
link to original post
You have the right idea and are within a penny of the answer. I verified my answer by compounding one million times per month in excelQuote: charliepatrickUsing a spreadsheet I get about $890.99. This was using the assumption where you're initially charged 40c on $40,000 for the first 1/1000th of a month, and similar logic thereafter.
If the interest is 12% per year, then it's 1% per month, so it's .001% per 1/1000th month, etc.
As a comparison if 12% were applied each year and you never paid anything back, then on $40k after 5 years I get it you owe $70,493.67 (1.12^5*40k). Whereas the 1/1000th method gives it at 72,884.53.
link to original post
For full credit, you must give an exact expression of the answer. It cannot be answered exactly to two decimal places.
History and Hint: The mathematical constant e was discovered by Bernoulli in 1683 while studying compound interest
Agree. 🍺Quote: ThatDonGuyQuote: Ace2Now for a truly easy math puzzle.
You take a 100 foot board, make one random cut and keep the shorter piece. Then you take another 100 foot board, make two random cuts and keep the shortest piece. Then you take another 100 foot board, make three random cuts and keep the shortest piece. This pattern continues forever.
What's the expected length of all the shortest pieces combined?
link to original post
The expected length of cutting a 100-foot board into N pieces is 100 / N^2, so the sum is 100 / 2^2 + 100 / 3^2 + 100 / 4^2 + ...
= 100 (1 / 2^2 + 1 / 3^2 + 1 / 4^2 + ...)
= 100 ((1 + 1 / 2^2 + 1 / 3^2 + 1 / 4^2 + ...) - 1)
= 100 (PI^2 / 6 - 1)
= 50 PI^2 / 3 - 100, or about 64.4934.
link to original post
Iím still amazed that the solution to this problem uses pi.
Quote: Ace2Disagree
link to original post
I misunderstood the question. So, the 12% interest gets compounded monthly, in other words 1% per month and that gets compounded infinitely. That said, I now get ...
To be more precise $890.995237303.
An exact expression is 40000/((1-(1/EXP(0.6)))/(EXP(0.01)-1))
Which is what I said.Quote: Ace2APR means annual percentage rate. The compounding interval is another variable. A normal car/house loan is paid back monthly and also compounded monthly. So for a 12% APR, 12% / 12 months per year = 1% of interest is added to the outstanding balance every month. This would be an APY (annual percentage yield) of 1.01^12 - 1 =~ 12.68%.
Quote: Ace2Compounded daily would be an APY of (1 + .12/365)^365 - 1 =~ 12.75%. For this problem, interest is compounded CONTINUOUSLY.
I will make some assumptions as to what you are asking...
When compounded continuously at n%, the effective annual rate is e^(n/100).
In this case, since payments are monthly, the principle is multiplied by (e^(12/100))^(1/12) = e^0.01 each month.
Using the payment calculation formula, I get 40,000 ((e^0.01) ^ 60) (e^0.01 - 1) / ((e^0.01) ^ 60 - 1)
= 40,000 (e^0.6) (e^0.01 - 1) / (e^0.6 - 1)
= about $891
Agree! 🍺Quote: WizardQuote: Ace2Disagree
link to original post
I misunderstood the question. So, the 12% interest gets compounded monthly, in other words 1% per month and that gets compounded infinitely. That said, I now get ...$891.00.
To be more precise $890.995237303.
An exact expression is 40000/((1-(1/EXP(0.6)))/(EXP(0.01)-1))
link to original post
The 12% APR gets compounded continuously, not monthly at 1%. Only the payments are monthly.
No. What you said was:Quote: ThatDonGuyWhich is what I said.Quote: Ace2APR means annual percentage rate. The compounding interval is another variable. A normal car/house loan is paid back monthly and also compounded monthly. So for a 12% APR, 12% / 12 months per year = 1% of interest is added to the outstanding balance every month. This would be an APY (annual percentage yield) of 1.01^12 - 1 =~ 12.68%.
Wrong.Quote: ThatDonGuyIf the APR is 12%, then the amount the principle is multiplied by each time for monthly payments is 1.12^(1/12).
Wrong. Very few people (mostly math nerds) even know what continuously compounded interest is. Iíve never actually seen it used for any financial instrument and Iím a seasoned finance guy. Have you ever seen a financial contract that lists the interest/payment terms using the mathematical constant e?Quote: ThatDonGuyAlso, doesn't "APR" always mean that the interest is compounded continuously?
You obviously did not understand what APR meant which is why I defined it for you.
Quote: Ace2Agree! 🍺
The 12% APR gets compounded continuously, not monthly at 1%. Only the payments are monthly.
link to original post
Thanks!
If the APR is i and it gets converted infinitely, then the effective annual interest rate is exp(i)-1.
So, at 12% APR, the actual interest rate after infinite compounding is exp(0.12) - 1 = 0.127497.
Next I had to calculate how much interest the rate was per month. Let that be m. Then:
(1+m)^12 = 1.127497
m = EXP(LN(1.127497)/12)-1 = 0.010050.
Next I use the standard amortization formula, which I've used on actuary exams many times.
Principle = Payment * (1-v^n)/i, where v = (1/(1+i)).
Here we have:
v = 1/(1+i) = 0.990050.
Principle = Payment * (1-v^n)/i.
40,000 = Payment * (1-0.990050^60)/0.010050
Payment = 40000/((1-0.990050^60)/0.010050) = 890.9952373
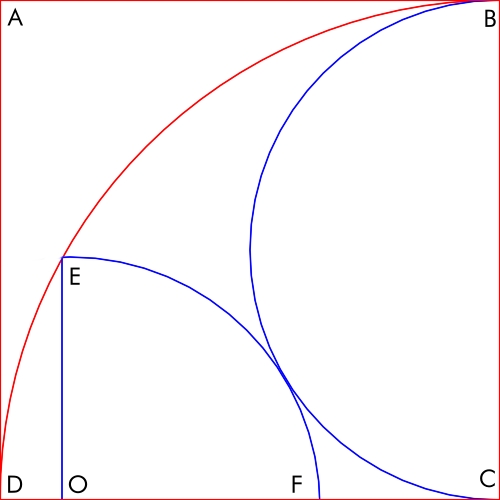
ABCD is a square of side length 10
BC, BD, and EF are circular arcs
EOF is a right angle
What is the length of OE?
Quote: ThatDonGuy
ABCD is a square of side length 10
BC, BD, and EF are circular arcs
EOF is a right angle
What is the length of OE?
link to original post
Disclaimer: I suck at geometry. Always have; always will.
Is there enough information here? You don't state that the arc BC is semicircle (so BC need not be the diameter: it could be any cord) and furthermore you don't state that arc BD is a quarter circle (so its center need not be C).
Intuitively it seems like if I make BD an arc of a huge circle that's centered very far "southeast" of C, and make arc BC the arc of a huge circle centered very far "east" of the midpoint of BC, I can get different answers for the length of OE. In particular, as the circle that contains arc BC gets bigger, the arc approaches a straight line (so it gets closer to the line BC). But then again I suck at geometry so my intuition may be off.
Quote: SkinnyTonyIs there enough information here? You don't state that the arc BC is semicircle (so BC need not be the diameter: it could be any cord) and furthermore you don't state that arc BD is a quarter circle (so its center need not be C).
BC is a semicircle, and EF and BD are quarter-circles.
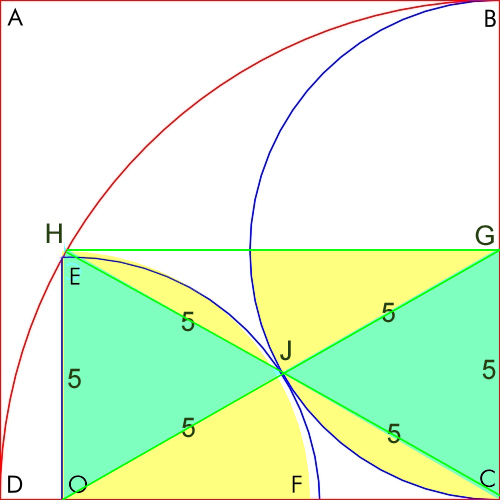
Quote: ThatDonGuyEOF is a right angle
What is the length of OE?
link to original post
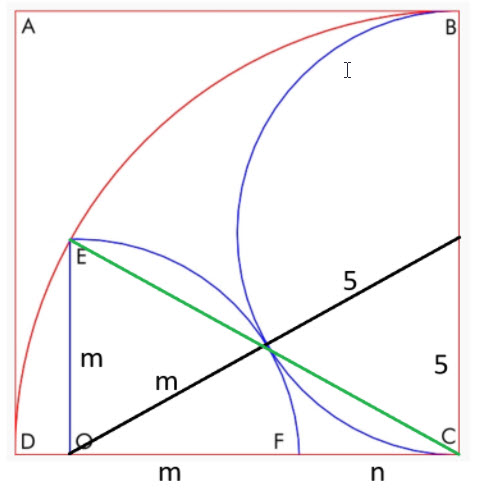
In this image we have two right triangles. Using Pythagorean, we have:
m^2 + (m+n)^2 = 100
(m+n)^2 + 25 = (m+5)^2
Two equations and two unknowns. The math is quite easy from here.
Quote: Ace2I never participate in the geometry problems and Iím probably wrong, but my answer is OE = 5.
link to original post
Quote: charliepatrickI agree that it's 5. Basically by construction one can enclose an equilateral triangle in the given quarter circle, and then consider what happens if you create a rectangle (CGHO). HC=10 since it's the radius of the largest circle, so OG is also 10. Therefore JG=CG=5 as radius of circle. Also OJ and OH are 5. Therefore there is a quarter circle through J and H with centre O which is 5. Therefore E is the same place as H.
link to original post
Quote: Wizard5
In this image we have two right triangles. Using Pythagorean, we have:
m^2 + (m+n)^2 = 100
(m+n)^2 + 25 = (m+5)^2
Two equations and two unknowns. The math is quite easy from here.
link to original post
All of you are correct. The solution I had is the one Wizard posted.
CharliePatrick, could you explain to me something in your solution?
Another way of looking at it, the angle of the tangent at J is 60 degrees because of the equilateral triangles and one of the sides is the radius.
Note: Reworded slightly at 8:22PM 11/2/25 PST.
Quote: WizardYou are at a 101-story building. Floors are numbered 0 to 100 (as most of the world numbers floors outside the US). You want to test for the highest floor you can safely drop an egg from into a large box of feathers on the ground. You know an egg dropped from the roof will break and one dropped from floor 0 will survive. You have two eggs only to experiment with. What is the fewest maximum number of drops you need?
link to original post
Quote: AutomaticMonkey
I'm struggling with the phrase "fewest maximum number" a bit. As I interpret it the answer is 1, being I could drop it from floor 100 and if it doesn't break or from floor 1 and it does break, there's my answer.
link to original post
I don't think this needed to be in a spoiler tag.
What I'm trying to ask is what strategy results in the least number of drops in a worst case scenario. I hope you won't mind me saying that if the first drop was from floor 100 and the egg broke, then you would need 99 more drops with the second egg to find the highest safe floor. So, that puts you at 100 drops as a worst case scenario if you start at floor 100.
Quote: WizardQuote: AutomaticMonkey
I'm struggling with the phrase "fewest maximum number" a bit. As I interpret it the answer is 1, being I could drop it from floor 100 and if it doesn't break or from floor 1 and it does break, there's my answer.
link to original post
...What I'm trying to ask is what strategy results in the least number of drops in a worst case scenario. ..
link to original post
OK, this might do it then.
Quote: AutomaticMonkey
34. Start by dropping one from floor 33. If it breaks, then I drop from floor 1, floor 2 ... to floor 32. If it doesn't break, I still have 2 intact eggs so I can try it again from floor 67 and if it breaks work my way from floor 34 to 66. If it didn't break from 67 then I go drop from 68 to 100.
link to original post
That is a valid strategy, but there is a better one.
Quote: WizardQuote: AutomaticMonkey
34. Start by dropping one from floor 33. If it breaks, then I drop from floor 1, floor 2 ... to floor 32. If it doesn't break, I still have 2 intact eggs so I can try it again from floor 67 and if it breaks work my way from floor 34 to 66. If it didn't break from 67 then I go drop from 68 to 100.
link to original post
That is a valid strategy, but there is a better one.
link to original post
Oh yeah...
Quote: WizardYou are at a 101-story building. Floors are numbered 0 to 100 (as most of the world numbers floors outside the US). You want to test for the highest floor you can safely drop an egg from into a large box of feathers on the ground. You know an egg dropped from the roof will break and one dropped from floor 0 will survive. You have two eggs only to experiment with. What strategy will result in a the least number of drops to guarantee finding the highest safe floor?
Note: Reworded slightly at 8:22PM 11/2/25 PST.
link to original post
Drop an egg from floor 9. If it does not break, then drop an egg from floor 22, then, in order, 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99, and 100; stop when one breaks or an egg dropped from floor 100 does not break.
If none of them break, then the highest safe floor is 100.
Otherwise, drop the other egg from the floor one above the last known safe floor, and go up one floor at a time until it breaks.
Quote: AutomaticMonkey
Increments of square root of the number of floors, 10, 20, 30... then plus 1, plus 2, plus 3... starting from the last safe floor that is a power of 10 once you break one. 19 drops?
link to original post
We're down to 19 drops, but there is still a better way.
Quote: ThatDonGuy
I think it's this:
Drop an egg from floor 9. If it does not break, then drop an egg from floor 22, then, in order, 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99, and 100; stop when one breaks or an egg dropped from floor 100 does not break.
If none of them break, then the highest safe floor is 100.
Otherwise, drop the other egg from the floor one above the last known safe floor, and go up one floor at a time until it breaks.
link to original post
I agree! My solution was slightly different, starting with a higher floor but them proceeding with the same strategy, but still ended up with the same maximum drops.
Stipulations:
1) There should be minimal changes
2) The dice cannot be modified
3) The flow of the game can't be changed. There shouldn't be any noticeable change to the game for people who aren't playing the pass line
4) Any modified payouts should be use a practical ratio
I believe this question has been asked before but I don't think an exact answer was given
Incidentally, I think a craps game advertised as zero-edge could attract lots of gamblers, even though the majority would continue playing place/buy/prop sucker bets
Consider the numbers 1+2+Ö+13=91
(i) Drop egg at #14. If breaks then try 1 thru 13. Max 14 drops
(Ii) Drop egg at #27 (14+13). If it breaks then try 15 thru 26. Max 14 drops.
etc. The pattern is after Nth drop you only need 14-N tries.
4/10 pays 2 to 1
5/9 pays 6 to 4
6/8 pays evens except hard way pays double
The downside would be a natural only pays 1 to 2.
The upside is no odds, no need for place bets, you can add or subtract at any time.
(c) Charlie !!
edit version 2
As above except winning hard ways pay 4, 3 and 2/1, with easy ways paying evens.
Quote: Ace2In the game of craps, the pass line has a house edge of 7/495. Find a way to make the house edge EXACTLY zero.
Stipulations:
1) There should be minimal changes
2) The dice cannot be modified
3) The flow of the game can't be changed. There shouldn't be any noticeable change to the game for people who aren't playing the pass line
4) Any modified payouts should be use a practical ratio
I believe this question has been asked before but I don't think an exact answer was given
Incidentally, I think a craps game advertised as zero-edge could attract lots of gamblers, even though the majority would continue playing place/buy/prop sucker bets
link to original post
Alternative 1:
Make a come out 11 a loser. Have a winning point pay true odds like an odds bet.
Pros: easy to implement. Dealers used to doing odds.
Cons: People wonít love a yo loser.
Alternative 2:
Have winning points pay out true odds except the 4 pays out 5/3 instead of 2/1.
Pros: just one change.
Cons: super annoying to make passline bet divisible by 3.
Alternative 3:
Make a 1/6 and 2/5 seven on come out a push. Pay true odds on making a point.
That said:
Option 1:
All bets must be in increments of $75.
If the player loses after a point of 6, he will lose $61 instead of the full $75.
Option 2:
All bets must be in increments of $125.
If the player win on a point of 6, he will be paid odds of 153 to 125.
61 to 75 and 153 to 125 are definitely not practical payout ratios (see stipulation #4). Without that stipulation, itís very simple to even out the game by paying a passline win at 251 to 244Öit works mathematically but would never work in a real craps gameQuote: WizardThe following is the best I can do. My goal was to make no event pay less than it already does. Secondly, to change as little as possible.
That said:
Option 1:
All bets must be in increments of $75.
If the player loses after a point of 6, he will lose $61 instead of the full $75.
Option 2:
All bets must be in increments of $125.
If the player win on a point of 6, he will be paid odds of 153 to 125.
link to original post
Quote: unJonQuote: Ace2In the game of craps, the pass line has a house edge of 7/495. Find a way to make the house edge EXACTLY zero.
Stipulations:
1) There should be minimal changes
2) The dice cannot be modified
3) The flow of the game can't be changed. There shouldn't be any noticeable change to the game for people who aren't playing the pass line
4) Any modified payouts should be use a practical ratio
I believe this question has been asked before but I don't think an exact answer was given
Incidentally, I think a craps game advertised as zero-edge could attract lots of gamblers, even though the majority would continue playing place/buy/prop sucker bets
link to original post
Alternative 1:
Make a come out 11 a loser. Have a winning point pay true odds like an odds bet.
Pros: easy to implement. Dealers used to doing odds.
Cons: People wonít love a yo loser.
Alternative 2:
Have winning points pay out true odds except the 4 pays out 5/3 instead of 2/1.
Pros: just one change.
Cons: super annoying to make passline bet divisible by 3.
Alternative 3:
Make a 1/6 and 2/5 seven on come out a push. Pay true odds on making a point.
link to original post
Error in my alternative 2. The payout on the 4 would need to be a double loss if it hits. So ignore that one.
A different alternative 2 would be if the point is 4 or 10 that making the point results in a push. Other points pay true odds. Come out roll is unchanged.
UnJon and CharlieP: your scores range from 1.62 to 3.94. They are high due to the percentage of resolutions affected and the number of changes. Paying point winners at true odds is major change and will also increase variance by about 33%.
My version has a score of 0.07


