Find the red area
Poll
 | 1 vote (25%) | ||
| No votes (0%) | |||
| | 2 votes (50%) | ||
| | 2 votes (50%) | ||
| | 2 votes (50%) | ||
| | 1 vote (25%) | ||
| No votes (0%) | |||
| | 1 vote (25%) | ||
| | 2 votes (50%) | ||
| | 1 vote (25%) |
4 members have voted
February 22nd, 2020 at 5:15:16 PM
permalink
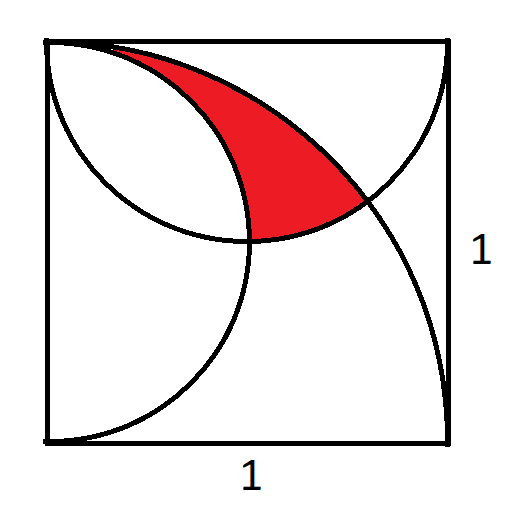
In the figure above, there is a quarter-circle and two semi-circles in a square of side length one. The question is what is the area of the red region?
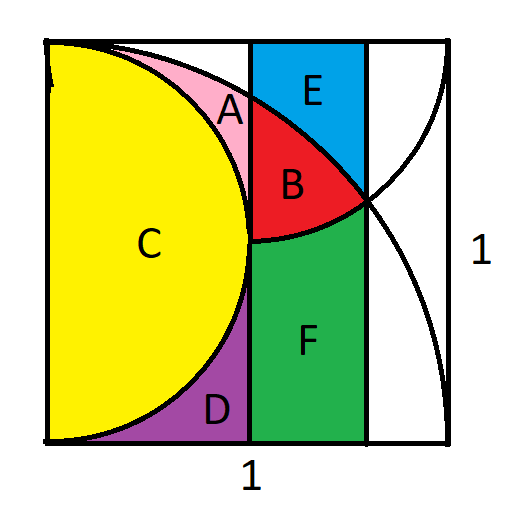
For purposes of discussion, may I suggest using this diagram to label various parts.
Finally, here is a integral you may find useful. I needed it to solve the problem.
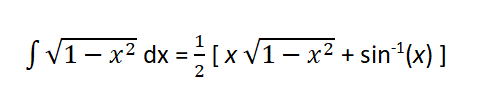
Usual rules:
- Please don't just plop a URL to a solution elsewhere until a winner here has been declared.
- All those who have won a beer previously are asked to not post answers or solutions for 24 after this posting. This rule has been violated by past winners the previous two problems. Past winners who must chime in early, may PM me.
- Beer to the first satisfactory answer and solution, subject to rule 2.
- Please put answers and solutions in spoiler tags.
The question for the poll is how do you feel about this puzzle?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 22nd, 2020 at 6:10:44 PM
permalink
This is way beyond any math that I ever learned, but I think that drawing those extra lines in that second image helps talk about it, but also give a big hint about how to solve it.
Then again its beyond my math abilities, so maybe its not a hint at all
Then again its beyond my math abilities, so maybe its not a hint at all
I invented a few casino games. Info:
http://www.DaveMillerGaming.com/
Superstitions are silly, childish, irrational rituals, born out of fear of the unknown. But how much does it cost to knock on wood? 😁
February 22nd, 2020 at 8:55:04 PM
permalink
There's various ways of solving it. My hint is not required for a more geometric solution. When in doubt, I prefer calculus.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 22nd, 2020 at 8:57:57 PM
permalink
Find the equations of the relevant curves, find the intersection points(integration limits) and than use integration to find area A and B separately. The intersection points a(0.8, 0.6) and b(0.5, 0.5).
x^2 + y^2 - x - 2y + 1 = 0 ...............Eq1
x^2 + y^2 -1= 0 ..................................Eq2
x^2 + y^2 - y= 0 .................................Eq3
Area A
Eq2 minus Eq1
Area B
Eq2 minus Eq3
See Pic below.
https://imge.to/i/y1HJNA
Area A + Area B = 0.09772, correct ?
https://imge.to/i/y1kKT1
x^2 + y^2 - x - 2y + 1 = 0 ...............Eq1
x^2 + y^2 -1= 0 ..................................Eq2
x^2 + y^2 - y= 0 .................................Eq3
Area A
Eq2 minus Eq1
Area B
Eq2 minus Eq3
See Pic below.
https://imge.to/i/y1HJNA
Area A + Area B = 0.09772, correct ?
https://imge.to/i/y1kKT1
Last edited by: ssho88 on Feb 23, 2020
February 23rd, 2020 at 6:45:47 AM
permalink
Quote: ssho88Area A + Area B = 0.09772, correct ?
Yes, that's correct.
I think the solution is difficult to follow, but I'll award you the beer nevertheless. Congratulations!
I am working on a more step by step solution, which I'll post later today, if all goes well.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 23rd, 2020 at 7:53:28 AM
permalink
Quote: WizardThere's various ways of solving it. My hint is not required for a more geometric solution. When in doubt, I prefer calculus.
That's where we differ - I prefer solutions that don't require calculus.
I have one, but the answer is expressed in terms of...
arcsin 3/5
February 23rd, 2020 at 12:13:26 PM
permalink
Here is my 6.5 page solution. The bottom line is also expressed as a function of what Don referred to in his spoiler.
Wizard solution (PDF)]
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 23rd, 2020 at 1:11:45 PM
permalink
Here is my solution:
Label the red area X, and the other five areas counterclockwise, A, B, C, D, and E (so, for example, C is the area touching the bottom edge, and D is the area touching the right edge)
E plus X is half of a circle of radius 1/2 minus section A:
Area(E) + Area(X) = 1/2 x PI x (1/2)2 - (PI/8 - 1/4) = 1/4
D plus E is a square of side length 1 minus 1/4 of a circle of radius 1:
Area(D) + Area(E) = 1 - 1/4 x PI x 12 = 1 - PI/4
Area(X) - Area(D) = (Area(X) + Area(E)) - (Area(E) + Area(D)) = 1/4 - (1 - PI/4) = PI/4 - 3/4
Area(X) = Area(D) + PI/4 - 3/4
Label the four corners of the square P, Q, R, S, clockwise from the upper left (e.g. the top edge is PQ, and the right edge is QR).
Let M be the midpoint of PQ, which is also the center of the top edge semicircle
Let O be the point where sections X, C, D, and E meet
Draw a line parallel to the right edge of the square that goes through O; let K be the endpoint of this line on PQ, and L be the endpoint of this line on RS
Let h = the length of KO; LO = 1 - h
Pythagorean Theorem: PK = 1/2 + sqrt(MO2 - KO2) = 1/2 + sqrt(1/4 - h2)
Pythagorean Theorem again: SL = sqrt(SO2 - LO2) = sqrt(1 - (1 - h)2) = sqrt(2h - h2)
KL is parallel to PS, so PK = SL -> 1/2 + sqrt(1/4 - h2) = sqrt(2h - h2)
Square both sides: 1/4 + (1/4 - h2) - 2 x 1/2 x sqrt(1/4 - h2) = 2h - h2
I will spare you the math: h = 2/5 -> MK = 3/10 -> KQ = LR = 1/5
Area(D) = the area of rectangle KQRL - the portion of the top semicircle in KQRL - the portion of the quarter circle in KQRL
KO = 2/5 and MO = 1/2 -> angle QMO = angle KMO = arcsin 4/5
The portion of the top semicircle in KQRL = PI x (1/2)2 x ((arcsin 4/5) / (2 PI)) - 1/2 x 2/5 x 3/10 = (arcsin 4/5) / 8 - 3/50
OL = 3/5 and SO = 1 -> angle RSL = angle LSO = arcsin 3/5
The portion of the quarter circle in KQRL = PI x 12 x ((arcsin 3/5) / (2 PI)) - 1/2 x 3/5 x 4/5 = (arcsin 3/5) / 2 - 6/25
Thus Area(D) = 1/5 - ((arcsin 3/5) / 8 - 3/50) - ((arcsin 4/5) / 2 - 6/25) = 1/2 - ((arcsin 4/5) / 8 + (arcsin 3/5) / 2)
Area(X) = Area(D) + PI/4 - 3/4
= 1/2 - ((arcsin 3/5) / 2 + (arcsin 4/5) / 2) + PI/4 - 3/4
= PI/4 - 1/4 - ((arcsin 3/5) / 2 + (arcsin 4/5) / 8))
However, arcsin 3/5 + arcsin 4/5 = PI/2
(proof: in a 3-4-5 right triangle, the angle opposite the length 3 side is arcsin 3/5, and the angle opposite the length 4 side is arcsin 4/5;
since they are the smaller angles of a right triangle, they sum to PI/2 radians)
Thus Area(X) = PI/4 - 1/4 - ((arcsin 4/5) / 8 + (arcsin 3/5) / 8 + 3/8 (arcsin 3/5))
= PI/4 - 1/4 - PI/16 - 3/8 arcsin 3/5
= 3/16 PI - 1/4 - 3/8 arcsin 3/5
= 0.0977357
Label the red area X, and the other five areas counterclockwise, A, B, C, D, and E (so, for example, C is the area touching the bottom edge, and D is the area touching the right edge)
E plus X is half of a circle of radius 1/2 minus section A:
Area(E) + Area(X) = 1/2 x PI x (1/2)2 - (PI/8 - 1/4) = 1/4
D plus E is a square of side length 1 minus 1/4 of a circle of radius 1:
Area(D) + Area(E) = 1 - 1/4 x PI x 12 = 1 - PI/4
Area(X) - Area(D) = (Area(X) + Area(E)) - (Area(E) + Area(D)) = 1/4 - (1 - PI/4) = PI/4 - 3/4
Area(X) = Area(D) + PI/4 - 3/4
Label the four corners of the square P, Q, R, S, clockwise from the upper left (e.g. the top edge is PQ, and the right edge is QR).
Let M be the midpoint of PQ, which is also the center of the top edge semicircle
Let O be the point where sections X, C, D, and E meet
Draw a line parallel to the right edge of the square that goes through O; let K be the endpoint of this line on PQ, and L be the endpoint of this line on RS
Let h = the length of KO; LO = 1 - h
Pythagorean Theorem: PK = 1/2 + sqrt(MO2 - KO2) = 1/2 + sqrt(1/4 - h2)
Pythagorean Theorem again: SL = sqrt(SO2 - LO2) = sqrt(1 - (1 - h)2) = sqrt(2h - h2)
KL is parallel to PS, so PK = SL -> 1/2 + sqrt(1/4 - h2) = sqrt(2h - h2)
Square both sides: 1/4 + (1/4 - h2) - 2 x 1/2 x sqrt(1/4 - h2) = 2h - h2
I will spare you the math: h = 2/5 -> MK = 3/10 -> KQ = LR = 1/5
Area(D) = the area of rectangle KQRL - the portion of the top semicircle in KQRL - the portion of the quarter circle in KQRL
KO = 2/5 and MO = 1/2 -> angle QMO = angle KMO = arcsin 4/5
The portion of the top semicircle in KQRL = PI x (1/2)2 x ((arcsin 4/5) / (2 PI)) - 1/2 x 2/5 x 3/10 = (arcsin 4/5) / 8 - 3/50
OL = 3/5 and SO = 1 -> angle RSL = angle LSO = arcsin 3/5
The portion of the quarter circle in KQRL = PI x 12 x ((arcsin 3/5) / (2 PI)) - 1/2 x 3/5 x 4/5 = (arcsin 3/5) / 2 - 6/25
Thus Area(D) = 1/5 - ((arcsin 3/5) / 8 - 3/50) - ((arcsin 4/5) / 2 - 6/25) = 1/2 - ((arcsin 4/5) / 8 + (arcsin 3/5) / 2)
Area(X) = Area(D) + PI/4 - 3/4
= 1/2 - ((arcsin 3/5) / 2 + (arcsin 4/5) / 2) + PI/4 - 3/4
= PI/4 - 1/4 - ((arcsin 3/5) / 2 + (arcsin 4/5) / 8))
However, arcsin 3/5 + arcsin 4/5 = PI/2
(proof: in a 3-4-5 right triangle, the angle opposite the length 3 side is arcsin 3/5, and the angle opposite the length 4 side is arcsin 4/5;
since they are the smaller angles of a right triangle, they sum to PI/2 radians)
Thus Area(X) = PI/4 - 1/4 - ((arcsin 4/5) / 8 + (arcsin 3/5) / 8 + 3/8 (arcsin 3/5))
= PI/4 - 1/4 - PI/16 - 3/8 arcsin 3/5
= 3/16 PI - 1/4 - 3/8 arcsin 3/5
= 0.0977357
February 23rd, 2020 at 5:52:34 PM
permalink
Quote: ThatDonGuy
= 3/16 PI - 1/4 - 3/8 arcsin 3/5
= 0.0977357
You can get rid of the pi term. That equates to (3/8)*arcsin(4/5) - 1/4
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
