Inscribed circle in a semicircle puzzle
February 16th, 2020 at 12:54:01 AM
permalink
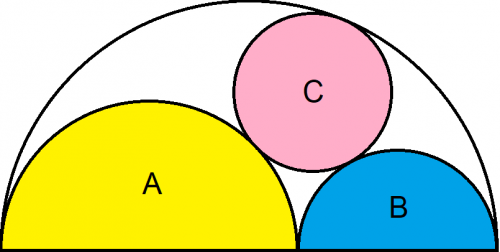
A and B are semicircles in in larger semicircle enclosing A, B, and circle C. Circle C is tangent to A, B, and the larger semicircle.
The base of A has length 6
The base of B has length 4
What is the radius of C?
Usual rules:
1. Please don't just plop a URL to a solution elsewhere until a winner here has been declared.
2. All those who have won a beer previously are asked to not post answers or solutions for 24 after this posting.
3. Beer to the first satisfactory answer and solution, subject to rule 2.
4. Please put answers and solutions in spoiler tags.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 16th, 2020 at 2:30:45 AM
permalink
Wizard, I've seen this before. Without pre-knowledge of Descartes' work, or google, I can't see anyone solving this on their own.
Psalm 25:16
Turn to me and be gracious to me, for I am lonely and afflicted.
Proverbs 18:2
A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.
February 16th, 2020 at 5:25:50 AM
permalink
Wiz,
Here's my solution:
Fun problem!
Dog Hand
Here's my solution:
Let's call the centers of the lettered circles Ca, Cb, and Cc, and their intersection points Tac and Tbc. Let r be the unknown radius of C, while the radii of A and B are 3 and 2, respectively.
Now since Tac is tangent to both A and C, we have a straight line passing from Ca through Tac to Cc with a length of 3+r. Similarly, since Tbc is tangent to both B and C, we have another straight line passing from Cb through Tbc to Cc with a length of 2+r. We also have a straight line from Ca to Cb with a length of 2+3=5.
These three lines from a right triangle with legs 2+r and 3+r and hypotenuse 5. From the Pythagorean Formula we get:
(2+r)^2 + (3+r)^2 = 5^2
r^2 +4r + 4 + r^2 + 6r + 9 =25
2r^2 + 10r - 12 = 0
r^2 + 5r - 6 = 0
So r = 1 is the only feasible solution.
Now since Tac is tangent to both A and C, we have a straight line passing from Ca through Tac to Cc with a length of 3+r. Similarly, since Tbc is tangent to both B and C, we have another straight line passing from Cb through Tbc to Cc with a length of 2+r. We also have a straight line from Ca to Cb with a length of 2+3=5.
These three lines from a right triangle with legs 2+r and 3+r and hypotenuse 5. From the Pythagorean Formula we get:
(2+r)^2 + (3+r)^2 = 5^2
r^2 +4r + 4 + r^2 + 6r + 9 =25
2r^2 + 10r - 12 = 0
r^2 + 5r - 6 = 0
So r = 1 is the only feasible solution.
Fun problem!
Dog Hand
February 16th, 2020 at 8:23:23 AM
permalink
Doghand, For triangle Ca-Cc-Cb, Pythagorean Formula only apply if angle Cc is 90 degree, how to prove that angle Cc is 90 degree ?
February 16th, 2020 at 8:24:52 AM
permalink
Even though it is almost noon here, my brain doesn't seem to be fully awake, so I have a question for Dog Hand (or others) about Dog Hand's solution. I'll hide it in a spoiler so I don't ruin things for others who want to work it out for themselves.
Edit: Ooops! Someone else asked basically the same thing while I was typing.
In Dog Hand's solution, he says, "These three lines from a right triangle with ...."
I interpreted his "from" as a typo for "form." If I interpreted that correctly, how is it established that these lines form a right triangle? How do we know that the Ca-Cc line is perpendicular to the Cb-Cc line?
I interpreted his "from" as a typo for "form." If I interpreted that correctly, how is it established that these lines form a right triangle? How do we know that the Ca-Cc line is perpendicular to the Cb-Cc line?
Edit: Ooops! Someone else asked basically the same thing while I was typing.
February 16th, 2020 at 9:07:33 AM
permalink
Quote: Wizard
A and B are semicircles in in larger semicircle enclosing A, B, and circle C. Circle C is tangent to A, B, and the larger semicircle.
The base of A has length 6
The base of B has length 4
What is the radius of C?
Usual rules:
1. Please don't just plop a URL to a solution elsewhere until a winner here has been declared.
2. All those who have won a beer previously are asked to not post answers or solutions for 24 after this posting.
3. Beer to the first satisfactory answer and solution, subject to rule 2.
4. Please put answers and solutions in spoiler tags.
I think can be solved as per attached image :-
https://ibb.co/D1T8vH1
Form 5 equations to solve for 5 unknown p, q, s, m and r ( radius of circle C ). L is center of larger semicircle.
Law of sines :-
1) LC/sin(p) = AL/sin(m)
2) LC/sin(q) = BL/sin(s)
3) AC/sin(q) = BC/sin(p)
4) AC/sin(q+s) = AL/sin(m)
5) p+q+m++s = 180
Last edited by: ssho88 on Feb 16, 2020
February 16th, 2020 at 10:11:27 AM
permalink
Quote: OnceDear
Wizard, I've seen this before. Without pre-knowledge of Descartes' work, or google, I can't see anyone solving this on their own.
Yes, this one is rather difficult and I admit I had to cheat myself. I'll give a hint if nobody can solve it without one.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 16th, 2020 at 10:18:46 AM
permalink
I'm having fun (perhaps) trying to find an angle of attack without looking up the hint you gave in an earlier spoiler.Quote: Wizard
Yes, this one is rather difficult and I admit I had to cheat myself. I'll give a hint if nobody can solve it without one.
Had to go out today so will look at Heron's forumla for area of triangles and seeing if it helps solves for r. Area = SQRT ( S (S-a)(S-b)(S-c) ) where S = (a+b+c)/2 .
February 16th, 2020 at 10:36:38 AM
permalink
I'll throw you a bone.... It boils down to solving a quadratic and does not need the use of trig functions.
Psalm 25:16
Turn to me and be gracious to me, for I am lonely and afflicted.
Proverbs 18:2
A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.
February 16th, 2020 at 10:42:10 AM
permalink
Quote: DogHandWiz,
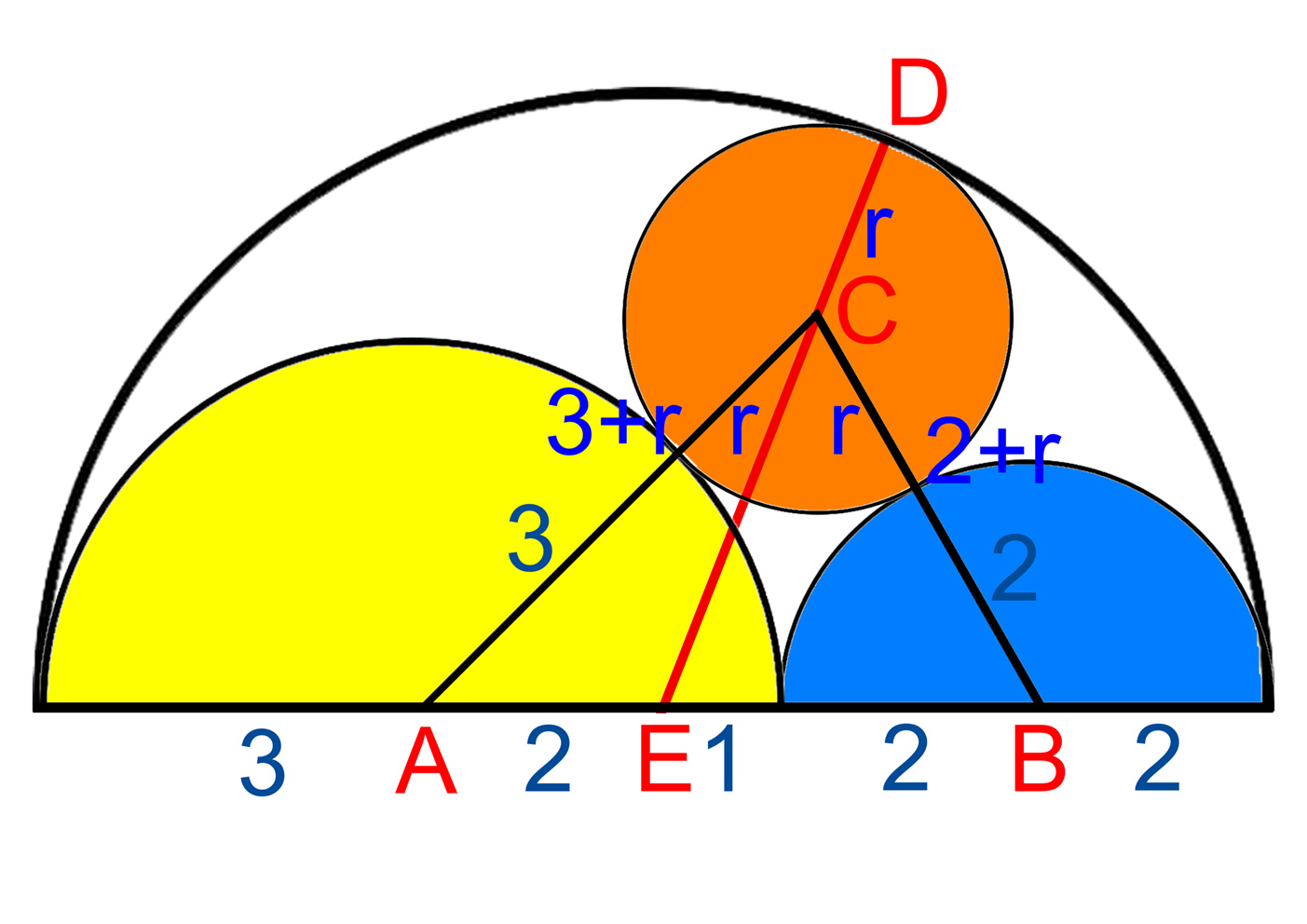
Here's my solution:Let's call the centers of the lettered circles Ca, Cb, and Cc, and their intersection points Tac and Tbc. Let r be the unknown radius of C, while the radii of A and B are 3 and 2, respectively.
Now since Tac is tangent to both A and C, we have a straight line passing from Ca through Tac to Cc with a length of 3+r. Similarly, since Tbc is tangent to both B and C, we have another straight line passing from Cb through Tbc to Cc with a length of 2+r. We also have a straight line from Ca to Cb with a length of 2+3=5.
These three lines from a right triangle with legs 2+r and 3+r and hypotenuse 5. From the Pythagorean Formula we get:
(2+r)^2 + (3+r)^2 = 5^2
r^2 +4r + 4 + r^2 + 6r + 9 =25
2r^2 + 10r - 12 = 0
r^2 + 5r - 6 = 0
So r = 1 is the only feasible solution.
Fun problem!
Dog Hand
I'm afraid I don't agree. Perhaps you're right and I'm wrong, but I don't think so.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 16th, 2020 at 10:44:58 AM
permalink
Quote: ssho88Form 5 equations to solve for 5 unknown p, q, s, m and r ( radius of circle C ). L is center of larger semicircle.
Law of sines :-
1) LC/sin(p) = AL/sin(m)
2) LC/sin(q) = BL/sin(s)
3) AC/sin(q) = BC/sin(p)
4) AC/sin(q+s) = AL/sin(m)
5) p+q+m++s = 180
I would have preferred you put that in spoiler tags. However, while those may be good hints, I don't see a correct answer in there.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 16th, 2020 at 10:47:04 AM
permalink
Quote: OnceDearI'll throw you a bone.... It boils down to solving a quadratic and does not need the use of trig functions.
It's too early to give hints. After the 24-hour waiting period, if none of the math geniuses on the forum solve it, I'll offer a hint.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 16th, 2020 at 11:57:41 AM
permalink
Quote: CharliePatrickI didn't need a quadratic so here goes.
Quote: WizardCharlie, congratulations, your answer is right and a well done solution.
However, it is in violation of the 24-hour rule. I have copied and pasted your post to you and will re-post it 24 hours from the OP, or you can do it.
If no previous winners get the answer within the 24 hour window, I will award you the beer.
Last edited by: unnamed administrator on Feb 16, 2020
February 17th, 2020 at 3:19:00 AM
permalink
Here is the answer and solution by Charlie, which I agree with. I busted this post earlier because it violated the 24-rule for previous winners.
Well done Charlie, I owe you another beer.
The way I did it does not require the use of Heron's formula, but the following formula...
Well done Charlie, I owe you another beer.
The way I did it does not require the use of Heron's formula, but the following formula...
Law of cosines:
a^2 = b^2 + c^2 - 2ab*cos(x),
where x is the angle opposite side a.
a^2 = b^2 + c^2 - 2ab*cos(x),
where x is the angle opposite side a.
Quote: CharliePatrickI didn't need a quadratic so here goes.
Construct a line (DE), since the angle at D is 90deg E is at the centre of the large circle.
So AE=2, EB=3 etc. as shown.
Consider area of triangles AEC and EBC (i) Using Height and Width /2, then (ii) using Heron's formula.
Area AEC = AE * height /2 = 2 h / 2.
Area EBC = EB * height / 2 = 3 h / 2.
So ratio of areas is 2 : 3.
Area AEC = SQRT of 5 (5-2) 5-(3+r) 5-(5-r) = SQRT of 5 3 2-r r = SQRT of 5r 2 3-r = SQRT of 5r (6-2r).
Area EBC = SQRT of 5 (5-3) 5-(5-r) 5-(2-r) = SQRT of 5r (6-2r).
So SQRT ( (6-3r) / (6-2r) ) = 2/3.
Squaring (6-3r)/(6-2r) = 4/9 or 52-47r = 24-8r or 30-19r = 0
... or r=30/19.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 17th, 2020 at 6:58:35 AM
permalink
I used law of cosines in early stage but could not solve it . . . .
I thought should be a^2 = b^2 + c^2 - 2bc*cos(x) ?
Edited, Finally I got it(Thanks Wizard !) :-
Triangle ABC
(3+r)^2 = 5^2 +(2+r)^2 - 2(5)(2+r)cos(B) -----Eq1
So, [(3+r)^2 - 5^2 -(2+r)^2]/5 = 2(2+r)cos(B) -----Eq2
Triangle EBC
(5-r)^2 = 3^2 +(2+r)^2 - 2(3)(2+r)cos(B) -----Eq3
So, [(5-r)^2 - 3^2 -(2+r)^2]/3 = 2(2+r)cos(B) -----Eq4
Then, Eq2 = Eq4
[(3+r)^2 - 5^2 -(2+r)^2]/5 = [(5-r)^2 - 3^2 -(2+r)^2]/3
r= 120/76 = 30/19
I thought should be a^2 = b^2 + c^2 - 2bc*cos(x) ?
Edited, Finally I got it(Thanks Wizard !) :-
Triangle ABC
(3+r)^2 = 5^2 +(2+r)^2 - 2(5)(2+r)cos(B) -----Eq1
So, [(3+r)^2 - 5^2 -(2+r)^2]/5 = 2(2+r)cos(B) -----Eq2
Triangle EBC
(5-r)^2 = 3^2 +(2+r)^2 - 2(3)(2+r)cos(B) -----Eq3
So, [(5-r)^2 - 3^2 -(2+r)^2]/3 = 2(2+r)cos(B) -----Eq4
Then, Eq2 = Eq4
[(3+r)^2 - 5^2 -(2+r)^2]/5 = [(5-r)^2 - 3^2 -(2+r)^2]/3
r= 120/76 = 30/19
Last edited by: ssho88 on Feb 17, 2020
February 17th, 2020 at 9:20:51 AM
permalink
You have to think outside of the circle.
It’s all about making that GTA
February 17th, 2020 at 9:38:23 AM
permalink
I solved it the way ssho88 did (after finally realizing that EC has length 5-r), but using triangles AEC and BEC, and noting that, since AEC = 180 - BEC, cos AEC = -cos BEC.
February 17th, 2020 at 11:13:35 AM
permalink
Click the spoiler for my solution, which uses the formula I given I already gave in a hint. It also proves that formula, so the only formulas required to know are:
Pythagorean and sin2φ + cos2φ = 1
Pythagorean and sin2φ + cos2φ = 1
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 17th, 2020 at 2:28:02 PM
permalink
I solved it without sin/cos. There are three unknowns (xc, y,c, rc) and three constraints:
Using the distance between two points (sqrt( (x1-x2)^2 + (y1-y2)^2)) I setup equations of the three known lengths in terms of xc, yc, and rc. I cheated and let python do the solving of the equations, so maybe these equations weren't easily solvable by hand.
- length of center of A to center of C = ra + rc
- length of center of B to center of C = rb + rc
- length of center of outer semicircle to center of C = ro - rc
Using the distance between two points (sqrt( (x1-x2)^2 + (y1-y2)^2)) I setup equations of the three known lengths in terms of xc, yc, and rc. I cheated and let python do the solving of the equations, so maybe these equations weren't easily solvable by hand.
# unknowns are (x,y) coordinates of circle C, and radius r of circle C
xc, yc, rc = sympy.symbols("xc yc rc")
# bounding semi-circle O is centered at (0,0),r=5
# semicircle A at (-2, 0), r=3
# semicircle B at ( 3, 0), r=2
len_ac = sympy.Eq(sympy.sqrt( (xc - -2 )**2 + (yc-0)**2 ), 3+rc)
len_bc = sympy.Eq(sympy.sqrt( (xc - 3) **2 + (yc-0)**2 ), 2+rc)
len_oc = sympy.Eq(sympy.sqrt( (xc - 0) **2 + (yc-0)**2 ), 5-rc)
February 18th, 2020 at 8:45:47 AM
permalink
Reply for wiz's solution:
Thank you for the answer. I believe it's the right answer. But can you explain that why the line WZ and the line from the center of C to the upper intersection is the same line?
or the better way to ask is : Why are W,Y and upper intersection points in the same line?
Thank you for the answer. I believe it's the right answer. But can you explain that why the line WZ and the line from the center of C to the upper intersection is the same line?
or the better way to ask is : Why are W,Y and upper intersection points in the same line?
Last edited by: MR.Z on Feb 18, 2020
February 18th, 2020 at 11:56:17 AM
permalink
I think you mean XZ. The reason is that the line from a circle to it's centre is at 90deg. So the line from the centre of the small circle to its edge, meets the arc at 90deg. Similarly the a line from the centre of the large circle to its edge will meet at 90deg. Since they meet the arc at the same point, it's the same line. In my diagram, hidden in this spoiler, it's ECD.Quote: MR.Z...wiz's solution...why the line WZ and the line from the center of C to the upper intersection is the same line...
