Poll
 | 1 vote (5.55%) | ||
 | 2 votes (11.11%) | ||
 | 6 votes (33.33%) | ||
 | 2 votes (11.11%) | ||
 | 1 vote (5.55%) | ||
 | 1 vote (5.55%) | ||
 | 4 votes (22.22%) | ||
 | 1 vote (5.55%) | ||
 | 1 vote (5.55%) | ||
 | 5 votes (27.77%) |
18 members have voted
First, imagine you are living in Flatland (a two-dimensional world). In this world there is long straight hallway of width 1. Eventually, this hallway makes a 90-degree turn. It then goes on for another long distance. The width of the hallway is always 1.
The question is what is the maximum size couch (in area) that you can move down this hallway. Here is a picture of the hallway, just in case anyone is lost already. You need to move a couch from x to y. Think of every grid was 1x1.
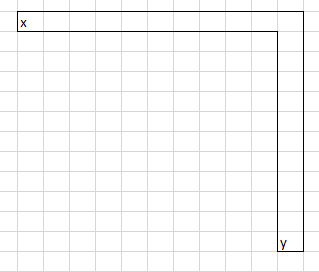
You could obviously slide a 1x1 square down the hallway, around the turn, and down the other way.
You could even move a semicircle of radius 1 down the hallway, pivot it 90 degrees clockwise at the corner, and then move it down the other way. Now you're at pi/2 in area.
However, there are known larger sizes that work. The largest side known so far does not have an elegant shape but is about 20 separate pieces strung together in sort of a banana shape.
It seems to be there should be some elegant solution to the problem, but nobody has proven a maximum possible solution thus far.
The question for the poll is what are your thoughts so far?
In either any case, I voted for asbergers. When I was in Vegas, a pit boss asked me if I was retarded. I replied "autism is a wide spectrum".
Quote: gamerfreakIt feels like this problem could be solved with a computer simulation, why is that not the case?
In either any case, I voted for asbergers. When I was in Vegas, a pit boss asked me if I was retarded. I replied "autism is a wide spectrum".
Damn, if that's the first time someone's called you retarded, you've been running pretty good. I think I average twice a day.
As far as the question:
1) I assume it can't have pivots or whatever you call them.....like a snake that can move side to side.
2) ThatDonGuy probably gonna come in here and give the most elegant and simplest proof ever, something like, "Since pi + 1 = 1 + pi...." and it'll actually make sense.
EDIT: For #1, more like a hinge I guess, like a door that has a hinge on it. Can my couch have hinges??
(1) I would use an inflatable couch and deflate it for the move.
(2) At a minimum, I would use a flexible couch.
Sorry to be so unresponsive.
Edit: I was typing while RS was posting.
Quote: gamerfreakIt feels like this problem could be solved with a computer simulation, why is that not the case?
Hmmm. I don't know too much about this, but I suspect human guided simulations brought us to the best known solution thus far. However, simulations are so unsatisfying, at least to me. Who can rest at night knowing the four-color map proof has allegedly been solved by computer? Not me.
Quote:In either any case, I voted for asbergers. When I was in Vegas, a pit boss asked me if I was retarded. I replied "autism is a wide spectrum".
Thanks. Best laugh I've had in at least a month. I'd love to hear the whole story.
Quote: RSEDIT: For #1, more like a hinge I guess, like a door that has a hinge on it. Can my couch have hinges??
In response this and Doc's post -- no, absolutely no moving parts. The couch is as solid as a rock.
I vote to pay for delivery and let the movers deal with the problem.
How big is the apartment? My couch is inflatable.🤓😜
Edit: this is not the right answer.
Quote: RSQuote: gamerfreakAs far as the question:
2) ThatDonGuy probably gonna come in here and give the most elegant and simplest proof ever, something like, "Since pi + 1 = 1 + pi...." and it'll actually make sense.
I heard that...
Actually, my first thought was that the problem was limited to "rectangular" couches. However, now that I see that the couch can be any two-dimensional shape, I have a feeling this is slightly above my mathematical expertise. I have a feeling the optimal shape is a portion of an ellipse/circle.
Quote: ThatDonGuyQuote: RS
I heard that...
Actually, my first thought was that the problem was limited to "rectangular" couches. However, now that I see that the couch can be any two-dimensional shape, I have a feeling this is slightly above my mathematical expertise. I have a feeling the optimal shape is a portion of an ellipse/circle.
Now I'm disappointed. :(

In addition to the rectangle there is another bit that could also be included - as the sofa rotates depending on the outside curve this defines what else can be added on the inside. I suspect it's a semi-circle for this shape.
Now by shaving bits here and there, one might be able to make the area larger with the rectangle bigger or the quarter circles slightly chubbier.
What seems obvious is that half way through the movement the shape round the corner is the same as the shape left to turn, so it must be symmetrical.
Quote: charliepatrickNot sure if this picture will work, if not consider a phone formed of two quarter circles (unit radius) with a join between them initially being a rectangle. The top of the rectangle joins the top of the quarters while the bottom just touches the corner at 45 degrees. Obviously a longer rectangle would be narrower, so there is an optimum size.
In addition to the rectangle there is another bit that could also be included - as the sofa rotates depending on the outside curve this defines what else can be added on the inside. I suspect it's a semi-circle for this shape.
Now by shaving bits here and there, one might be able to make the area larger with the rectangle bigger or the quarter circles slightly chubbier.
What seems obvious is that half way through the movement the shape round the corner is the same as the shape left to turn, so it must be symmetrical.
Couldn't those little triangles in the center of the "phone" be filled in?
Yes - as I said that adds even more. The objective here was to show the answer was more than the semi-circle solution. Where the outsides are circular, the inside will be circular (or in this case a semi-circle).Quote: gamerfreakQuote: charliepatrick....In addition to the rectangle there is another bit that could also be included - as the sofa rotates depending on the outside curve this defines what else can be added on the inside. I suspect it's a semi-circle for this shape....
Couldn't those little triangles in the center of the "phone" be filled in?
Quote: charliepatrick
Charlie, are you sure you could even get the couch into, and out of, that position? Remember that you have to move the couch around the corner.
However, your basic shape is not that far from the best-known solutions thus far.
The tough thing about this problem is that it is a moving problem. I know calculus is the mathematics of change but somehow I don't think it will help us with this. I can't think of any better solution than brute force trial and error. As soon as I have some more free time I plan to give this problem the ol' college try.
Following is in in-depth video on the problem.
I'm sure it couldn't! On reflection the bottom of the rectangle has to be in line with the points of contact, also at that point the inside shape should be a circle. Indeed it may show the outside curves are as well, but I've yet to analyze that. As you say there's lots of interesting reading about it although I may fall down when the integration comes into play! Thanks for posting the puzzle.Quote: Wizard...are you sure you could even get the couch into, and out of, that position?...
I've been accused of having Asperger's before. I think it's possible but so slight it doesn't really have much of a negative impact on my life. Aside from my terrible social skills, I guess.
Quote: TigerWuThere's a known maximum size the couch can be
erm. No there isn't. That is at the heart of the issue.
Quote: OnceDearerm. No there isn't. That is at the heart of the issue.
This is what I mean:
Take a theoretical couch you know will fit around the corner. Add x amount of area. See if that still works. If it does, add x again. Keep going until you've reached a size that won't fit around the corner no matter how little area you've added or where you've added it. That is your maximum limit. I don't understand why that can't be done, if not by a person, then certainly by a computer.
There's a saying that you can prove something exists but it's harder to prove something particular doesn't exist. With the former you just have to find it, where, unless you can show some sort of contradiction, not finding one doesn't prove it doesn't exist.
i imagined a twinky shaped item, with a flat rectangular section in the middle and a quarter circle on each side. sort of like the phone, but the bottom is one constant line. a 4 sided shape with two of the sides being arcs, tangent to the top line. the middle section is of length X, and the arcs of radius R. a semicircle described in the problem statement would be this shape with X=0, R=1. i tried to attach a sketch, but that doesn't seem to be working for whatever reason.
i figured the 45 degree state was the critical section, so i put the 'couch' there at 45 degrees with the middle of the bottom line being right at the corner. going to the right, the hallway is a width of 1, so X/2*cos(45)+R = 1. the area of the couch is R^2*pi/2 + R*X = A.
by replacing X=(1-R)*2/cos(45) and taking the derivative, i find a maximum area of 1.59 sq units. pi/2 ~= 1.57 so maybe i've found a bigger couch. however i checked what values for R and X gave this geometry, it was for R=1.1245 and x = -.3521. this couch fits in the 45 degree position, but not in the flat section of the hallway. also it crosses over itself for some goofy areas. having a -X value is a little nonsensical.

The two ends of the couch are Reuleaux triangles, which have a constant diameter.
I have no idea about other solutions, and I came up with this one playing around with my compass.
Quote: TigerWuIf you have a bean bag couch you can make it infinitely long and it will still be able to squish around the corner.... :D
You're late.
Quote: CrystalMathHere is what I came up with:...
Very nice. I can see how it would pivot around the corner. Best answer from this group so far. That gives us something to strive to beat at least.

Someone better at calculus or with more time than me could optimize the distance between my two original pieces (now quarter circles).
Never mind. The optimal distance is trivial. Center area = 2r- pi*r^2/2 . A simple derivative reveals the optimal radius is 2/pi.
Given that distance (as opposed to the one shown in the picture), the area is pi/2 + 4/pi - pi(2/pi)^2 / 2 = 2.2074.
I don't see any reason why this wouldn't work, but I don't totally trust it because my area is greater than Gerver's Sofa. Although I don't entirely trust it, I did re-do the calculations twice and came to the same conclusion.

Quote: CrystalMathI was hoping to be done with this, since I'm obsessing about it.
I would apologize but I don't want to lie to you. Who knows what kind of greatness is born out of such obsession.
I was obsessed with solving the Eternity II puzzle for months. Unfortunately, it turned out to be a huge waste of time. But I enjoyed the pursuit nonetheless.
I think that in your 8/4 solution, as the couch moves along, there are two points each touching an inner wall, with the two ends of the couch slowly rotating about those sliding points.
If I have that correct, I don't understand how that translates to the latest solution. Instead of points, each end of the couch seems to be shown as having a short, flat, contact surface against an inner wall. I don't see how those flat surfaces will both rotate and maintain contact with the wall as the couch slides, the way that point contacts can. Perhaps the point/flat could be replaced with an appropriately curved surface to slide along the wall and rotate?
Am I missing something?
Quote: DocCrystalMath: Maybe I am just so clueless that I don't understand how your latest solution makes the turn.
I think that in your 8/4 solution, as the couch moves along, there are two points each touching an inner wall, with the two ends of the couch slowly rotating about those sliding points.
If I have that correct, I don't understand how that translates to the latest solution. Instead of points, each end of the couch seems to be shown as having a short, flat, contact surface against an inner wall. I don't see how those flat surfaces will both rotate and maintain contact with the wall as the couch slides, the way that point contacts can. Perhaps the point/flat could be replaced with an appropriately curved surface to slide along the wall and rotate?
Am I missing something?
I think you got it right. The inner points need to be much more curved than I originally thought. I could have the same effect with the other points, but I'd need to remove much more area. Of course, it could be some balance between them.
It seems that the inner curve on CM's latest solution (the phone receiver shape) would be elliptical - not uniformly radiused - in the direction that reduces the area slightly. Just a gut feeling... I haven't started with arts and crafts yet!
* Spell checker makes me capitalize that.
Quote: WizardI'm thinking of buying a block of Styrofoam* and material to build a track just to see what I come up with. I would keep shaving the Styrofoam until it fit around the corner.
* Spell checker makes me capitalize that.
It is trademarked by Dow Chemical.
https://en.m.wikipedia.org/wiki/Styrofoam
Quote: IbeatyouracesIt is trademarked by Dow Chemical.
https://en.m.wikipedia.org/wiki/Styrofoam
Sheesh. Do I have to capitalize Jacuzzi* as well?
* My spell checker says "yes." That has become an everyday word in the English language.
Quote: WizardSheesh. Do I have to capitalize Jacuzzi* as well?
* My spell checker says "yes." That has become an everyday word in the English language.
Sheldon Cooper


