Imagine this math problem

Threads: 1520
Posts: 27126

Joined: Oct 14, 2009

April 25th, 2016 at 7:20:36 PM permalink

What is the answer to this problem?

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

beachbumbabs

beachbumbabs

Threads: 101
Posts: 14268

Joined: May 21, 2013

April 25th, 2016 at 7:27:05 PM permalink

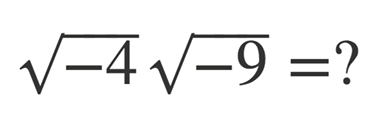
Quote: Wizard
What is the answer to this problem?

I don't think it's possible to have a square root of a negative number, because any 2 negs multiplied are a positive number.

However, if we ignore the square root function for the moment (not sure if that's a legal operation, but say it is) and just multiply 4*9, then take the square root of that, the multiplication having wiped out the 2 negative values, then it's the square root of 36, or 6.

If the House lost every hand, they wouldn't deal the game.

andysif

andysif

Threads: 23
Posts: 433

Joined: Aug 8, 2011

April 25th, 2016 at 7:55:52 PM permalink

Quote: beachbumbabs
Quote: Wizard
What is the answer to this problem?

I don't think it's possible to have a square root of a negative number, because any 2 negs multiplied are a positive number.

However, if we ignore the square root function for the moment (not sure if that's a legal operation, but say it is) and just multiply 4*9, then take the square root of that, the multiplication having wiped out the 2 negative values, then it's the square root of 36, or 6.

indeed you can. that number is called "i" and it's quite common in engineering and higher math.

rsactuary

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

April 25th, 2016 at 8:15:56 PM permalink

to be more specific, the square root of -1 is defined as i, or similarly defined as i^2 = -1

Doc

Threads: 46
Posts: 7287

Joined: Feb 27, 2010

April 25th, 2016 at 8:31:16 PM permalink

It has been so long since I have worked with imaginary numbers that this is all I come up with:

Sqrt{A} * Sqrt{B] = Sqrt{A * B}.

Sqrt{-4} * Sqrt{-9} = Sqrt{-4 * -9}
                            = Sqrt{36}
                            = ± 6

(I apologize if the character ± doesn't come through correctly. It is supposed to be the +/- symbol.)

Alternatively:

Sqrt{-4} * Sqrt{-9} = (Sqrt{4} * Sqrt{-1}) * (Sqrt{9} * Sqrt{-1})
                            = (±2 * i) * (±3 * i )
                            = ±6 * i^2
                            = ±6 * -1
                            = ±6

This leads to the poll answer of "Either 6 or -6", but I'm not certain that is correct. Senility can be a bitch.

TomG

TomG

Threads: 16
Posts: 2466

Joined: Sep 26, 2010

April 25th, 2016 at 10:13:28 PM permalink

2i * 3i or 2 * 3 * i * i or 2 * 3 * -1 = -6

I don't see how it could be 6, but it's late and I'm not going to work it out any more than once tonight

andysif

andysif

Threads: 23
Posts: 433

Joined: Aug 8, 2011

April 25th, 2016 at 10:36:09 PM permalink

Quote: TomG

2i * 3i or 2 * 3 * i * i or 2 * 3 * -1 = -6

I don't see how it could be 6, but it's late and I'm not going to work it out any more than once tonight

multiply what ever is in the sq rt first and you get sq rt of 36, which could be either 6 or -6

RS

Threads: 62
Posts: 8626

Joined: Feb 11, 2014

April 25th, 2016 at 11:39:01 PM permalink

i think:

(-4)^1/2 * (-9)^1/2 =
2i * 3i =
6i^2 =
6 * (-1)^1/2

andysif

andysif

Threads: 23
Posts: 433

Joined: Aug 8, 2011

April 26th, 2016 at 12:24:15 AM permalink

Quote: RS
i think:

(-4)^1/2 * (-9)^1/2 =
2i * 3i =
6i^2 =
6 * (-1)^1/2

something wrong going from line 3 to line 4
i^2 is already -1

davethebuilder

davethebuilder

Threads: 10
Posts: 73

Joined: Jan 11, 2015

April 26th, 2016 at 2:27:57 AM permalink

Quote: Wizard
What is the answer to this problem?
Last edited by: davethebuilder on Apr 26, 2016

Casino Enemy No.1

davethebuilder

davethebuilder

Threads: 10
Posts: 73

Joined: Jan 11, 2015

April 26th, 2016 at 2:54:10 AM permalink

Solve: √-4*√-9
= √(-1)*(4)√(-1)*(9)
= √-1*√4*√-1*√9
= i*2*i*3
= 2i*3i
= (2i)*(3i)
= (2*3)*(i*i)
= 6*i²
= -6

Apologies - moderators, please hide this in a spoiler. (done...BBB)

Last edited by: beachbumbabs on Apr 26, 2016

Casino Enemy No.1

odiousgambit

odiousgambit

Threads: 327
Posts: 9776

Joined: Nov 9, 2009

April 26th, 2016 at 3:57:09 AM permalink

to see how the spoiler is done, hit 'quote' on a post where someone did it

I won't try to answer, as it throws me to think a negative times a negative is negative

the next time Dame Fortune toys with your heart, your soul and your wallet, raise your glass and praise her thus: �Thanks for nothing, you cold-hearted, evil, damnable, nefarious, low-life, malicious monster from Hell!� She is, after all, stone deaf. ... Arnold Snyder

ChesterDog

ChesterDog

Threads: 9
Posts: 1732

Joined: Jul 26, 2010

April 26th, 2016 at 5:06:20 AM permalink

Quote: Wizard
What is the answer to this problem?

The "order of operations" convention (see Mathworld) is important for this problem. Taking the square roots should be done first and then the multiplication (2i * 3i; 2i * 3i = -6). If the multiplication of the insides of the radicals was done first [sqrt(36); sqrt(36) = 6)], an erroneous result would occur.

Doc

Threads: 46
Posts: 7287

Joined: Feb 27, 2010

April 26th, 2016 at 6:11:50 AM permalink

I think that a number of the "solutions" shown behind spoilers have made the same assumption, and I am not sure whether it is correct. They seem to

assume that √X means "the positive square root of X", which is the way I have sometimes heard it used. If that is the case, then I am not sure what symbol is properly used for "the square root of X." If the question had simply been

√4 = ?

would the proper answer have been 2 or ±2 ?

(And yes, I finally found the √ character on my keyboard. Hope it comes through as a square root function symbol. I'm not sure that these extended characters always look the same to everyone.)

Romes

Romes

Threads: 29
Posts: 5624

Joined: Jul 22, 2014

April 26th, 2016 at 7:22:28 AM permalink

Quote: TomG

2i * 3i or 2 * 3 * i * i or 2 * 3 * -1 = -6

I don't see how it could be 6, but it's late and I'm not going to work it out any more than once tonight

This was precisely my thinking...

√-4 = i√4 = 2i
√-9 = i√9 = 3i

Thus, you have i*2*i*3, which is the same as 2i*3i or 3*2*i^2...

i^2 = -1, thus, you have 3*2*-1 = -6

Playing it correctly means you've already won.

CrystalMath

CrystalMath

Threads: 8
Posts: 1911

Joined: May 10, 2011

April 26th, 2016 at 7:33:02 AM permalink

The easiest way, which shouldn't give much headache is to realize that this is the square root of (-4)(-9), or 36. The square root of 36 is, of course, +-6.

Alternatively, if you take the roots independently, you get (+-2i)(+-3i). Multiplying these, you'll get +-(-6), which is +-6.

I heart Crystal Math.

ThatDonGuy

ThatDonGuy

Threads: 123
Posts: 6745

Joined: Jun 22, 2011

April 26th, 2016 at 7:45:24 AM permalink

(2i)² = -4, but (-2i)² = -4 as well.
Therefore, both 2i and -2i are square roots of -4, just as 2 and -2 are both square roots of 4.

Similarly, (3i)² = -9, but (-3i)² = -9 as well.
Therefore, both 3i and -3i are square roots of -9.

2i x 3i = -6
2i x (-3i) = 6
(-2i) x 3i = 6
(-2i) x (-3i) = -6
Therefore, the solutions are 6 and -6.

TwoFeathersATL

TwoFeathersATL

Threads: 37
Posts: 3616

Joined: May 22, 2013

April 26th, 2016 at 7:49:12 AM permalink

Not good at math, that's me.
But I prefer math questions that have one correct answer, positive or negative.
And the end of a session the bankroll is up or down, I have not seen it be both, yet ;-)

Youuuuuu MIGHT be a 'rascal' if.......(nevermind ;-)...2F

beachbumbabs

beachbumbabs

Threads: 101
Posts: 14268

Joined: May 21, 2013

April 26th, 2016 at 8:14:19 AM permalink

Quote: CrystalMath

The easiest way, which shouldn't give much headache is to realize that this is the square root of (-4)(-9), or 36. The square root of 36 is, of course, +-6.

Alternatively, if you take the roots independently, you get (+-2i)(+-3i). Multiplying these, you'll get +-(-6), which is +-6.

Yay CM! I've missed you!

If the House lost every hand, they wouldn't deal the game.

Joeman

Joeman

Threads: 36
Posts: 2454

Joined: Feb 21, 2014

April 26th, 2016 at 8:16:09 AM permalink

-6

Taking the square root of each number gives you 2i * 3i = 6i²

Since i = sq. root of -1, i² = -1, and 6 * -1 = -6

"Dealer has 'rock'... Pay 'paper!'"

Wizard
Administrator

Threads: 1520
Posts: 27126

Joined: Oct 14, 2009

April 26th, 2016 at 8:37:15 AM permalink

+/- 6

I'm not saying this is correct, especially before teliot gives me my usual intellectual beating when I attempt a math problem. However, here it goes...

sqrt(-4) * sqrt(-9) =
sqrt(4) * sqrt(-1) * sqrt(-9) * sqrt(-1) =
+/- 2 * i * +/- 3 * i =
+/- 6 * -1 =
-/+ 6 =
6 or -6

Okay, Eliot, bring it on.

Last edited by: Wizard on Apr 26, 2016

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Doc

Threads: 46
Posts: 7287

Joined: Feb 27, 2010

April 26th, 2016 at 9:15:38 AM permalink

I disagree with part of the Wizard's solution.

The Wizard said:

sqrt(-4) * sqrt(-9) =
sqrt(4) * sqrt(i) * sqrt(-9) * sqrt(i) = ....

I suspect he meant:

sqrt(-4) * sqrt(-9) =
sqrt(4) * sqrt(-1) * sqrt(9) * sqrt(-1) =
sqrt(4) * i * sqrt(9) * i = ....

But I shouldn't try to put words in his mouth.

RS

Threads: 62
Posts: 8626

Joined: Feb 11, 2014

April 26th, 2016 at 9:25:15 AM permalink

Quote: RS
i think:

(-4)^1/2 * (-9)^1/2 =
2i * 3i =
6i^2 =
6 * (-1)^1/2

Edit:

im Retarded.

Should be:

6i^2 = 6 * i^2 = 6 * -1 = -6

-6

Not seeing how to get +6...?

MrGoldenSun

MrGoldenSun

Threads: 3
Posts: 252

Joined: Apr 1, 2016

April 26th, 2016 at 10:20:04 AM permalink

My vote is:

-6.

I typically interpret the square root sign to mean only the positive root, so if you asked me for sqrt(25) I'd simply say 5, not "5 or -5." In this case I interpret it to mean the root with a positive sign associated, so I end up with 2i*3i = -6

Or you could pull out the negatives to change it to sqrt(4)*sqrt(-1)*sqrt(9)*sqrt(-1) = 2*i*3*i = -6.

Wizard
Administrator

Threads: 1520
Posts: 27126

Joined: Oct 14, 2009

April 26th, 2016 at 10:22:36 AM permalink

Quote: Doc
I disagree with part of the Wizard's solution.

You're right.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

MathExtremist

MathExtremist

Threads: 88
Posts: 6526

Joined: Aug 31, 2010

April 26th, 2016 at 10:37:50 AM permalink

and that meaning is "the principal square root". http://mathworld.wolfram.com/SquareRoot.html . The answer to the question as written is -6.

"In my own case, when it seemed to me after a long illness that death was close at hand, I found no little solace in playing constantly at dice." -- Girolamo Cardano, 1563

TheGrimReaper13

Threads: 0
Posts: 216

Joined: Sep 25, 2015

April 26th, 2016 at 10:48:16 AM permalink

Quote: MathExtremist
and that meaning is "the principal square root". http://mathworld.wolfram.com/SquareRoot.html . The answer to the question as written is -6.

Poor mathematical advice.

So much bullshit; so little time!

MathExtremist

MathExtremist

Threads: 88
Posts: 6526

Joined: Aug 31, 2010

April 26th, 2016 at 10:52:08 AM permalink

Quote: TheGrimReaper13
Quote: MathExtremist
and that meaning is "the principal square root". http://mathworld.wolfram.com/SquareRoot.html . The answer to the question as written is -6.
Poor mathematical advice.

From Wolfram? Surely you jest.

"In my own case, when it seemed to me after a long illness that death was close at hand, I found no little solace in playing constantly at dice." -- Girolamo Cardano, 1563

TheGrimReaper13

Threads: 0
Posts: 216

Joined: Sep 25, 2015

April 26th, 2016 at 10:53:10 AM permalink

Surely, you paraphrase.

So much bullshit; so little time!

MathExtremist

MathExtremist

Threads: 88
Posts: 6526

Joined: Aug 31, 2010

April 26th, 2016 at 11:05:08 AM permalink

Quote: TheGrimReaper13
Surely, you paraphrase.

Nope:

Quote: Wolfram MathWorld
For example, the principal square root of 9 is , while the other square root of 9 is .
...
For example, using the imaginary unit i, the two square roots of -9 are . The principal square root of a number z is denoted (as in the positive real case) and is returned by the Wolfram Language function Sqrt[z].

The point is that if the problem had been asking for both square roots of -9, it would have been denoted

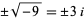. Then you can get to +/- 6.

"In my own case, when it seemed to me after a long illness that death was close at hand, I found no little solace in playing constantly at dice." -- Girolamo Cardano, 1563

OnceDear

Threads: 64
Posts: 7543

Joined: Jun 1, 2014

April 26th, 2016 at 11:09:14 AM permalink

Quote: TheGrimReaper13
Quote: MathExtremist
and that meaning is "the principal square root". http://mathworld.wolfram.com/SquareRoot.html . The answer to the question as written is -6.
Poor mathematical advice.

Au contraire. I learned something there. The same assertion as to the meaning of that 'radical' sign is made here: https://www.mathsisfun.com/square-root.html

Quote:
Well the square root of 25 could be −5 or +5.
But when we use the radical symbol √ we only give the positive (or zero) result.
Example: What is √36 ?

Answer: 6 × 6 = 36, so √36 = 6

Based on that definition, fwiw, I believe the Wizards answer is uncharacteristically wrong!!!

Psalm 25:16 Turn to me and be gracious to me, for I am lonely and afflicted. Proverbs 18:2 A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.

TheGrimReaper13

Threads: 0
Posts: 216

Joined: Sep 25, 2015

April 26th, 2016 at 11:29:13 AM permalink

"Any non-negative real number x has a unique non-negative square root r; this is called the principal square root and is written r=x^(1/2) or r=sqrt(x). For example, the principal square root of 9 is sqrt(9)=+3, while the other square root of 9 is -sqrt(9)=-3."

The question isn't about, "any non-negative real number x... ."

So much bullshit; so little time!

OnceDear

Threads: 64
Posts: 7543

Joined: Jun 1, 2014

April 26th, 2016 at 11:38:39 AM permalink

Quote: TheGrimReaper13
The question isn't about, "any non-negative real number x... ."

The question IS about a specific mathematical formula using very specific symbols such as the 'minus' sign '-' and the 'radical' sign '√' in a specific written order.
Just as the order of precedence is an explicit and integral part of Mathematics, so is the very explicit meanings and usage of those symbols.
I was not previously aware that the √ deliberately restricts the resolved square root to one of the two possible values, but I do accept that that is exactly what the definitions that I can locate are telling me.

I would SO LOVE to see Mike pop by to either confirm that his answer is incorrect, or else to dispute the assertion that he was wrong, citing definitions that go to the heart of the question.

Psalm 25:16 Turn to me and be gracious to me, for I am lonely and afflicted. Proverbs 18:2 A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.

OnceDear

Threads: 64
Posts: 7543

Joined: Jun 1, 2014

April 26th, 2016 at 11:50:26 AM permalink

Quote: Doc
I think that a number of the "solutions" shown behind spoilers have made the same assumption, and I am not sure whether it is correct. They seem to
assume that √X means "the positive square root of X", which is the way I have sometimes heard it used. If that is the case, then I am not sure what symbol is properly used for "the square root of X." If the question had simply been

√4 = ?

would the proper answer have been 2 or ±2 ?

(And yes, I finally found the √ character on my keyboard. Hope it comes through as a square root function symbol. I'm not sure that these extended characters always look the same to everyone.)

√4 = 2
√4 <> -2

Because, apparently, and remarkably the √ does not mean 'square root of' but does mean 'positive square root of'

Psalm 25:16 Turn to me and be gracious to me, for I am lonely and afflicted. Proverbs 18:2 A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.

APEppink

APEppink

Threads: 14
Posts: 69

Joined: Aug 20, 2013

April 26th, 2016 at 12:14:25 PM permalink

+-6, principle root = -6

BleedingChipsSlowly

BleedingChipsSlowly

Threads: 23
Posts: 1035

Joined: Jul 9, 2010

April 26th, 2016 at 12:39:59 PM permalink

Didn't read all posts, but I see i and its square root are covered. I voted for -6. Had the problem specified + and - square roots I would have voted 6 or -6.

�You don�t bring a bone saw to a negotiation.� - Robert Jordan, former U.S. ambassador to Saudi Arabia

Doc

Threads: 46
Posts: 7287

Joined: Feb 27, 2010

April 26th, 2016 at 12:55:09 PM permalink

Quote: OnceDear
I would SO LOVE to see Mike pop by to either confirm that his answer is incorrect, or else to dispute the assertion that he was wrong, citing definitions that go to the heart of the question.

If the Wizard's answer (as amended by my earlier post) is incorrect, then I think it is only by the interpretation of the √symbol, as I questioned on page 2 & OnceDear quoted in another post above, and which has become a topic of discussion. If that really is the case, it certainly appears that MathExtremist and CrystalMath have taken opposite sides.

OnceDear

Threads: 64
Posts: 7543

Joined: Jun 1, 2014

April 26th, 2016 at 1:11:51 PM permalink

Quote: Doc
If the Wizard's answer (as amended by my earlier post) is incorrect, then I think it is only by the interpretation of the √symbol, as I questioned on page 2 & OnceDear quoted in another post above, and which has become a topic of discussion. If that really is the case, it certainly appears that MathExtremist and CrystalMath have taken opposite sides.

It's indeed absolutely remarkable. I had never been aware of the interpretation of the √symbol to mean what I now determine it to mean, so up until this morning, I would have sided with Wizard. But such maths symbols only have one meaning. It's just a matter now of agreeing which and who's definition of that meaning has the greatest authority. Wikipedia and Wolfram define it but I acknowledge that they are not authoritative. DIN1302 might seem a place to start. . . . or ISO 80000-2 which in item number 2-9.11 has this to say ...

"The symbol √a should be avoided"

http://www.ise.ncsu.edu/jwilson/files/mathsigns.pdf

Last edited by: OnceDear on Apr 26, 2016

Psalm 25:16 Turn to me and be gracious to me, for I am lonely and afflicted. Proverbs 18:2 A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.

odiousgambit

odiousgambit

Threads: 327
Posts: 9776

Joined: Nov 9, 2009

April 26th, 2016 at 1:20:43 PM permalink

If I can take away anything from this, may I ask if this conclusion is right?

the square root of -4 has no solution by itself

the square root of -9 has no solution by itself

however, the square root of -4 times the square root of -9 does have a solution

?????????????

the next time Dame Fortune toys with your heart, your soul and your wallet, raise your glass and praise her thus: �Thanks for nothing, you cold-hearted, evil, damnable, nefarious, low-life, malicious monster from Hell!� She is, after all, stone deaf. ... Arnold Snyder

CrystalMath

CrystalMath

Threads: 8
Posts: 1911

Joined: May 10, 2011

April 26th, 2016 at 1:35:50 PM permalink

Quote: Doc
If the Wizard's answer (as amended by my earlier post) is incorrect, then I think it is only by the interpretation of the √symbol, as I questioned on page 2 & OnceDear quoted in another post above, and which has become a topic of discussion. If that really is the case, it certainly appears that MathExtremist and CrystalMath have taken opposite sides.

I often learn things from MathExtremist.

I had no idea that I could not simply multiply the numbers under the radical before computing the square root. √-4 * √-9 does not equal √36, since one is positive and the other negative.

I heart Crystal Math.

OnceDear

Threads: 64
Posts: 7543

Joined: Jun 1, 2014

April 26th, 2016 at 1:37:42 PM permalink

Quote: odiousgambit
If I can take away anything from this, may I ask if this conclusion is right?

the square root of -4 has no solution by itself

the square root of -9 has no solution by itself

however, the square root of -4 times the square root of -9 does have a solution

?????????????

ODG,
the square root of -4 has solution = (±4 x square root of -1) =±4i Unless you use the √ symbol which restricts us to +4i

If you are familiar with complex numbers where -1^0.5 has the value i ( or j in engineering parlance) then all is clear(er). But not everyone is familiar with complex numbers so don't beat yourself up about it if you are one of those people. Seldom relevant in a casino setting $:o)

Psalm 25:16 Turn to me and be gracious to me, for I am lonely and afflicted. Proverbs 18:2 A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.

Wizard
Administrator

Threads: 1520
Posts: 27126

Joined: Oct 14, 2009

April 26th, 2016 at 1:40:46 PM permalink

Quote: MathExtremist
The point is that if the problem had been asking for both square roots of -9, it would have been denoted . Then you can get to +/- 6.

I must admit that this business of the primary square root is new to me. If I can take this as true, then my answer posted earlier would be wrong. Wikipedia backs up ME's position on this.

Quote: Wikipedia
Every positive number a has two square roots: √a, which is positive, and −√a, which is negative. Together, these two roots are denoted ± √a (see ± shorthand). Although the principal square root of a positive number is only one of its two square roots, the designation "the square root" is often used to refer to the principal square root.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

OnceDear

Threads: 64
Posts: 7543

Joined: Jun 1, 2014

April 26th, 2016 at 2:53:08 PM permalink

Quote: Wizard
I'll go.

Don't bother. It's got no atmosphere.

I know. I'll get me coat.

Psalm 25:16 Turn to me and be gracious to me, for I am lonely and afflicted. Proverbs 18:2 A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.

RS

Threads: 62
Posts: 8626

Joined: Feb 11, 2014

April 26th, 2016 at 2:59:02 PM permalink

I don't know how to make fancy letters, so I gotta use CODE.....but...


           ____________
\         /
  \     /         9
    \ /

Solution is ONLY +3?

For it to be -3, there would have to be a minus '-' sign to the left of the funny shape (radical?)??

And for +/-3, it'd have to have a +/- sign in front of the radical?

Instead of 9, what if it's -9?

Answer can only be 3i, still? Something quoted above made it seem like it only counted or something if the number was positive..not sure if that means the number inside the radical must be positive....or if it's talking about the sign to the left of the radical?

TheGrimReaper13

Threads: 0
Posts: 216

Joined: Sep 25, 2015

April 26th, 2016 at 3:11:21 PM permalink

Quote: TwoFeathersATL
There seems to still be some confusion on this, someone said it was 'common' in engineering circles. Are we still planning to send men/women to Mars? Have any of you volunteered to go?

"Principal Square Root

The unique non-negative square root of a non-negative real number. For example, the principal square root of 9 is 3, although both -3 and 3 are square roots of 9.

The concept of principal square root cannot be extended to real negative numbers since the two square roots of a negative number cannot be distinguished until one of the two is defined as the imaginary unit, at which point +i and -i can then be distinguished. Since either choice is possible, there is no ambiguity in defining i as "the" square root of -1."

http://mathworld.wolfram.com/PrincipalSquareRoot.html

What this amounts to is that imaginary numbers aren't inherently positive or negative. Like Hawking's concept of imaginary time with no beginning or end; like the extended complex numbers have -infinity = +infinity; like i^2 = +1 in the semi-quaternions.

Which leads us to the trouble with "cherry picking" math problems on gambling forums, or the internet, itself, for that matter.

"Since either choice is possible... ."

So much bullshit; so little time!

AxelWolf

AxelWolf

Threads: 170
Posts: 22695

Joined: Oct 10, 2012

April 26th, 2016 at 3:27:16 PM permalink

Since its imaginary I imagine you're missing an H.

https://www.youtube.com/watch?v=xi4kP_KGo9A

♪♪Now you swear and kick and beg us That you're not a gamblin' man Then you find you're back in Vegas With a handle in your hand♪♪ Your black cards can make you money So you hide them when you're able In the land of casinos and money You must put them on the table♪♪ You go back Jack do it again roulette wheels turinin' 'round and 'round♪♪ You go back Jack do it again♪♪

TheGrimReaper13

Threads: 0
Posts: 216

Joined: Sep 25, 2015

April 26th, 2016 at 3:31:21 PM permalink

Quote: AxelWolf
Since its imaginary I imagine you're missing an H.

My middle initial.

So much bullshit; so little time!

Wizard
Administrator