That said, i am hitting a brick wall with my math. I am relatively good at math, but I lack understanding in probability theory and when to calculate combinations and permutations &c...
For now I am looking at single throws of 6 fair 6 sided dice. I may look at multiple throws (like in Yahtzee) later on, but for now I will try and keep it as simple as possible.
The problem I have is that while the dice are numbered 1 through 6 as standard, the faces have alternating colours. 3 of the dice will have red odd numbers and black even numbers and the other 3 will have black odd numbers and red even numbers.
e.g.
Die 1 - 1 2 3 4 5 6
Die 2 - 1 2 3 4 5 6
Die 3 - 1 2 3 4 5 6
Die 4 - 1 2 3 4 5 6
Die 5 - 1 2 3 4 5 6
Die 6 - 1 2 3 4 5 6
In amongst looking for the number of ways I can make (exactly!!!) 1 pair, 2 pair, 3 pair, 1 triple, 1 triple/1 pair, 2 triple, 1 quad, 1 quad/1 pair, 1 quint, 1 sextupelet and 1 6 dice straight. I am also looking to include how these can be matched (same colour) or mixed (different colours). With the quad, there are 2 mix possibilities 3/1 and 2/2.
I am not looking fo the answers, but rather help in calculating them.
Any advice on getting excel or similar to be able to help would also be appreciated.
Fun problem.Quote: CmdrBondI am not looking fo the answers, but rather help in calculating them.
Any advice on getting excel or similar to be able to help would also be appreciated.
I love colors, not just red and black, so I would have to think more about the color part too.
I would suggest here for the math understanding
http://blog.plover.com/math/yahtzee.html
my table doing the math looks like this
something to compare to
Index1 = 6!
Index2 = for AA edit: AA = one pair only
I use 6 choose 2 (6*5/2*1) * 6
*5*4*3*2 for BCDE =
15*6 * 5*4*3*2 = 10800
| index | pattern | ways | probability | 1 in |
|---|---|---|---|---|
| 1 | ABCDEF | 720 | 0.015432099 | 64.80 |
| 2 | AABCDE | 10800 | 0.231481481 | 4.32 |
| 3 | AABBCD | 16200 | 0.347222222 | 2.88 |
| 4 | AABBCC | 1800 | 0.038580247 | 25.92 |
| 5 | AAABCD | 7200 | 0.154320988 | 6.48 |
| 6 | AAABBC | 7200 | 0.154320988 | 6.48 |
| 7 | AAABBB | 300 | 0.006430041 | 155.52 |
| 8 | AAAABC | 1800 | 0.038580247 | 25.92 |
| 9 | AAAABB | 450 | 0.009645062 | 103.68 |
| 10 | AAAAAB | 180 | 0.003858025 | 259.20 |
| 11 | AAAAAA | 6 | 0.000128601 | 7,776.00 |
| total | 46,656 |
Sally
Just so I am clear, is this just for the matching the numbers and not worrying about colour - i.e. treating them as normal dice?
Not a problem if it is, as it gives a base to start from.
also, could you explain
Quote:Index1 = 6!
Index2 = for AA
I use 6 choose 2 *6 (6*5/2*1)
*5*4*3*2 BCDE
I understand 6!, I am guessing that 6 factorial (6*5*4*3*2*1) gives the total number of permutations for 6 dice labeled A-F.
I also understand C(6,2) as the number of positions that any 2 dice can hold within the 6.
I don't understand multiplying by 6(6*5/2*1)
I also don't understand the *5*4*3*2 except that I believe those numbers to apply to the remaining singletons.
Thanks for taking an interest.
yes, exactlyQuote: CmdrBondJust so I am clear, is this just for the matching the numbers and not worrying about colour - i.e. treating them as normal dice?
Not a problem if it is, as it gives a base to start from.
Oops, I got sloppy with the 6(6*5/2*1)Quote: CmdrBondalso, could you explain
I don't understand multiplying by 6(6*5/2*1)
6C2 = (6*5/2*1) is what I was after
nice catch and *6 because A can be any of 6 values
Sure looks fun at this point in time.Quote: CmdrBondI also don't understand the *5*4*3*2 except that I believe those numbers to apply to the remaining singletons.
Thanks for taking an interest.
You also guessed correctly the 5*4*3*2
for the colors, I think we have to get into the partitions for each of the patterns
but I still need to get back to that later after some reading
Sally
The number of permutations of N items that are in K groups, with a1, a2, ..., aK being the number of times the items in each group appear (so a1 + ... + aK = N) is:
N! / (a1! x a2! x ... x aK!)
For example, the number of permutations of 6 dice which are 2-2-6-6-3-5 is 6! / (2! x 2! x 1! x 1!) = 720 / 4 = 180.
Quote: ThatDonGuyHere is something you will find useful:
The number of permutations of N items that are in K groups, with a1, a2, ..., aK being the number of times the items in each group appear (so a1 + ... + aK = N) is:
N! / (a1! x a2! x ... x aK!)
For example, the number of permutations of 6 dice which are 2-2-6-6-3-5 is 6! / (2! x 2! x 1! x 1!) = 720 / 4 = 180.
OK. I think I follow that - I will have to sit and digest it a bit more.
How does that expand out to multiple groups?
Also, how would we categorise the groups.
I see groups A-F for the dice, 1-6 for the numbers and red/black for the faces.
The number 1 would appear on 6 dice, on 3 red faces and 6 black faces.
Whereas dice A appears once in each number group once and in each coloured face group 3 times.
And a Red face would appear in each number group 3 times and each die group 3 times.
How wrong am I getting this?
The thread in question is here:note there I have also given the dice 6 suits as well as their numbers and colours. I have decided to just worry about the numbers and colours for the time being, the suits make it overly complex.
Please note that credit for most of what lies below is down to other contributors on that thread, and that (shock horror) I have just realised they have told me some of the same things you guys have. I am still confused though.
From that thread though, here are some reasonings - firstly for 1 pair and 4 singletons.
Any one pair, and no more:
C(6,1) = 6 - The pair can be 1 of 6 numbers
C(6,2) = 15 - The pair can be made from 2 of the 6 dice
C(5,4) = 5 - The 4 singletons can be among the other 5 numbers
P(4!) = 24 - The number of ways the singletons can be arranged
(6*15*5*24)/(6^6) = 10800/46656 = 25/108
Any one odd pair (black and red)
C(6,1) = 6 - The pair can be 1 of 6 numbers
C(3,1) = 3 - 1 of the 3 black dice
C(3,1) = 3 - 1 of the 3 red dice
C(5,4) = 5 - The 4 singletons can be among the other 5 numbers
P(4!) = 24 - The number of ways the singletons can be arranged
(6*3*3*5*24)/(6^6) = 6480/46656 = 5/36 = 15/108
Any one matched pair (black and black or red and red)
C(6,1) = 6 - The pair can be 1 of 6 numbers
C(2,1) = 2 - The colour of the pair (black or red)
C(3,2) = 3 - 2 of the 3 dice of the same colour
C(5,4) = 5 - The 4 singletons can be among the other 5 numbers
P(4!) = 24 - The number of ways the singletons can be arranged
(6*2*3*5*24)/(6^6) = 4320/46656 = 5/54 = 10/108
and 10/108 + 15/108 = 25/108
I them came to those same results via a different angle
For any 1 pair (either matched or unmatched) and no other matching numbers.
6/6 - The 1st number can be anything.
1/6 - The 2nd number can only be 1/6 numbers.
5/6 - The 3rd number does not match any previously rolled.
4/6 - The 4th number does not match any previously rolled.
3/6 - The 5th number does not match any previously rolled.
2/6 - The 6th number does not match any previously rolled.
15/1 - The number of ways the dice can be arranged. C(6,2)
6 x 1 x 5 x 4 x 3 x 2 x 15 10800 25
-------------------------- = ----- = ---
6 x 6 x 6 x 6 x 6 x 6 x 1 46656 108
For 1 pair of mixed colours and no other matching numbers
6/6 - The 1st number can be anything.
1/10 - The 2nd number can only be 1/6 numbers and can only appear on 3/5 dice. 1/6 x 3/5 = 3/30 = 1/10
5/6 - The 3rd number does not match any previously drawn.
4/6 - The 4th number does not match any previously drawn.
3/6 - The 5th number does not match any previously drawn.
2/6 - The 6th number does not match any previously drawn.
15/1 - The number of ways the dice can be arranged. C(6,2)
6 x 1 x 5 x 4 x 3 x 2 x 15 10800 5 15
---------------------------- = ----- = -- = ---
6 x 10 x 6 x 6 x 6 x 6 x 1 77760 36 108
For 1 pair of the same colour and no other matching numbers.
6/6 - The 1st number can be anything.
1/15 - The 2nd number can only be 1/6 numbers and can only appear on 2/5 dice. 1/6 x 2/5 = 2/30 = 1/15
5/6 - The 3rd number does not match any previously rolled.
4/6 - The 4th number does not match any previously rolled.
3/6 - The 5th number does not match any previously rolled.
2/6 - The 6th number does not match any previously rolled.
15/1 - The number of ways the dice can be arranged. C(6,2)
6 x 1 x 5 x 4 x 3 x 2 x 15 10800 5 10
---------------------------- = ------ = -- = ---
6 x 15 x 6 x 6 x 6 x 6 x 1 116640 54 108
I then tried to rationalise this process to choosing 2 pairs, and while I seem to have got the correct figures for specific 2 pairs, my calculation for any 2 pair (excluding 2 triples, a "full house", or 4 of a kind yada yada) seemed to be off by more than double.
For any 2 distinct pairs (either matched or unmatched) and no other matching numbers.
6/6 - The 1st number can be anything.
1/6 - The 2nd number matches the first.
5/6 - The 3rd number does not match any previously rolled.
1/6 - The 4th number matches the 3rd.
4/6 - The 5th number does not match any previously rolled.
3/6 - The 6th number does not match any previously rolled.
15/1 - The number of ways the 1st pair can be arranged. C(6,2)
6/1 - the number of ways the 2nd pair can be arranged. C(4,2)
6 x 1 x 5 x 1 x 4 x 3 x 15 x 6 32400 25 100
------------------------------ = ----- = -- = ---
6 x 6 x 6 x 6 x 6 x 6 x 1 x 1 46656 36 144
For 2 distinct pairs, 1 matched and 1 unmatched.
6/6 - The 1st number can be anything.
1/15 - The 2nd number can only be 1/6 numbers and can only appear on 2/5 dice. 1/6 x 2/5 = 2/30 = 1/15
5/24 - The 3rd number can only be 5/6 numbers and appear on 1/4 dice. 5/6 x 1/4 = 5/24 (It does not matter if black or red is rolled, this is the last die that matches the odd/even colour sequence of the first 2).
1/6 - The 4th number matches the 3rd. (No need to worry about the dice pattern, they are all the same now)
4/6 - The 5th number does not match any previously rolled.
3/6 - The 6th number does not match any previously rolled.
15/1 - The number of ways the 1st pair can be arranged. C(6,2)
6/1 - the number of ways the 2nd pair can be arranged. C(4,2)
6 x 1 x 5 x 1 x 4 x 3 x 15 x 6 32400 10
------------------------------- = ------ = ---
6 x 15 x 24 x 6 x 6 x 6 x 1 x 1 466560 144
For 2 distinct pairs, both matched.
6/6 - The 1st number can be anything.
1/15 - The 2nd number can only be 1/6 numbers and can only appear on 2/5 dice. 1/6 x 2/5 = 2/30 = 1/15
5/8 - The 3rd number can only be 5/6 numbers and appear on 3/4 dice. 5/6 x 3/4 = 15/24 = 5/8
1/12 - The 4th number can only be 1/6 and appear on 1/2 dice. 1/6 x 1/2 = 1/12
4/6 - The 5th number does not match any previously rolled.
3/6 - The 6th number does not match any previously rolled.
15/1 - The number of ways the 1st pair can be arranged. C(6,4)
6/1 - the number of ways the 2nd pair can be arranged. C(4,2)
6 x 1 x 5 x 1 x 4 x 3 x 15 x 6 32400 5 15
------------------------------- = ------ = -- = ---
6 x 15 x 8 x 12 x 6 x 6 x 1 x 1 311040 48 144
For 2 distinct pairs, both unmatched.
6/6 - The 1st number can be anything.
1/10 - The 2nd number can only be 1/6 numbers and can only appear on 3/5 dice. 1/6 x 3/5 = 3/30 = 1/10
5/12 - The 3rd number can only be 5/6 numbers and appear on 2/4 dice. 5/6 x 2/4 = 10/24 = 5/12 (It does not matter if black or red is rolled, this is the last die that matches the odd/even colour sequence of the first 2).
1/9 - The 4th number can only be 1/6 and appear on 2/3 dice. 1/6 x 2/3 = 2/18 = 1/9
4/6 - The 5th number does not match any previously rolled.
3/6 - The 6th number does not match any previously rolled.
15/1 - The number of ways the 1st pair can be arranged. C(6,4)
6/1 - the number of ways the 2nd pair can be arranged. C(4,2)
6 x 1 x 5 x 1 x 4 x 3 x 15 x 6 32400 5 20
------------------------------- = ------ = -- = ---
6 x 10 x 12 x 9 x 6 x 6 x 1 x 1 233280 36 144
I think I still have something wrong though - as my number of specific distinct pairs (aa/aa, aa/ab and ab/ab) should equal my total number of pairs - but there is a difference of 55/144!
10/144 + 15/144 + 20/144 = 45/144 yet I get 100/144 for my "any 2 distinct pairs" combo.
One of the other guys over there reckons that
2 matched pairs: 5/72
1 matched pair and 1 unmatched pair: 5/36
2 unmatched pairs: 5/36
Die 1 = 11,12,13,14,15,16
Die 2 = 21,22,23,24,25,26
Die 3 = 31,32,33,34,35,36
etc...
This might also help after you have the table of all potential outcomes with creating formulae to determine the win/loss scenarios for each iteration.
You could use conditional formatting to give the cells the right coloring easily enough.
Building the table by brute force is going to be rough if you can't think of a way to automate it.
Quote: CmdrBondI then tried to rationalise this process to choosing 2 pairs, and while I seem to have got the correct figures for specific 2 pairs, my calculation for any 2 pair (excluding 2 triples, a "full house", or 4 of a kind yada yada) seemed to be off by more than double.
For any 2 distinct pairs (either matched or unmatched) and no other matching numbers.
6/6 - The 1st number can be anything.
1/6 - The 2nd number matches the first.
5/6 - The 3rd number does not match any previously rolled.
1/6 - The 4th number matches the 3rd.
4/6 - The 5th number does not match any previously rolled.
3/6 - The 6th number does not match any previously rolled.
15/1 - The number of ways the 1st pair can be arranged. C(6,2)
6/1 - the number of ways the 2nd pair can be arranged. C(4,2)6 x 1 x 5 x 1 x 4 x 3 x 15 x 6 32400 25 100
------------------------------ = ----- = -- = ---
6 x 6 x 6 x 6 x 6 x 6 x 1 x 1 46656 36 144
You're counting every set twice.
Example: 6,6,5,5,4,3 - since you count 15 ways to arrange the first pair, then they can be the first and last numbers, and since you count 6 ways to arrange the second pair, then they can be the second and fifth numbers, so 6, 5, 3, 4, 5, 5 is one of the counted rolls for "first pair 6s, second pair 5s".
However, with 5,5,6,6,4,3 - the 5s can be the second and fifth numbers, and the 6s can be the first and last numbers, so 6, 5, 3, 4, 5, 5 is also one of the counted rolls for "first pair 5s, second pair 6s".
15/36 - first two dice have to be different, and in order
1/6 - third die matches the first
1/6 - fourth die matches the second
4/6 - fifth die does not match any of the first four
3/6 - sixth die does not match any of the first five
15/1 - number of ways the first/third dice pair can be arranged
6/1 - number of ways the second/fourth dice pair can be arranged
15 x 1 x 1 x 4 x 3 x 15 x 6 16200 25
-------------------------- = ----- = --
36 x 6 x 6 x 6 x 6 x 1 x 1 46656 72
Wow, nice.Quote: ThatDonGuyYou're counting every set twice.
15/36 - first two dice have to be different, and in order
1/6 - third die matches the first
1/6 - fourth die matches the second
4/6 - fifth die does not match any of the first four
3/6 - sixth die does not match any of the first five
15/1 - number of ways the first/third dice pair can be arranged
6/1 - number of ways the second/fourth dice pair can be arranged
15 x 1 x 1 x 4 x 3 x 15 x 6 16200 25
-------------------------- = ----- = --
36 x 6 x 6 x 6 x 6 x 1 x 1 46656 72
this seems to make it more difficult to follow, at least for me, if every step was done right.
The link I provided shows a few simple ways (opinion) to do these pattern type problems and what to watch out for.
Especially the double-counting.
There are actually many methods to attack pattern type problems.
I do these type of pattern problems a few different ways too, just on how I see it in my mind.
AABBCD
2 pair
AA= 6C2 = 15 (we have 6 and want 2)
BB= 4C2 = 6 (we have 4 and want 2)
C= 2C1 = 2
D= 1C1 = 1
15*6*2*1 = 180
But AABB and BBAA are the same so we need to divide out those two (2!) as order here does not matter
also CD and DC are the same so another 2! to divide out
180 / 2!*2! = 180/4=45
A can be 6 values
B:5
C:4
D:3
45*6*5*4*3 = 16,200
For AABBCC = 3 pair
AA= 6C2 = 15
BB= 4C2 = 6
CC= 2C2 = 1
The order does not matter
for 3 pairs we simply have 3! to divide out
15*6*1 / 6=15
the values
A=6
B=5
C=4
15*6*5*4= 1800
AAABBB
2 trips
AAA = 6C3 = 6*5*4/3*2*1 = 20
BBB = 3C3 = 1
order does not matter so again divide out the 2 trips with 2!
20/2 = 10
values would be 6 and 5 so
10*6*5 = 300
These problems still also give me major headaches, I do not know why
I have not done the colors yet
need to rest
Sally
Quote: BuzzardIf you want, I can do the colors. Oh by the way, I checked all your previous calculations and did not find any errors.
What would this forum do without it's resident funny man :)
You say the rest of my math is OK, but there is still a discrepancy.
The total number of distinct 2 pairs is 25/72 (50/144).
The numbers I got for 2 distinct matched pair, 2 distinct mixed pair and 2 distinct pair where 1 is mixed and 1 is matched are
5/48, 5/36 and 5/72 or 15/144, 20/144 and 10/144 which totals 45/144.
According to the guys at BoardGameGeek, it should be 5/36, 5/36 and 5/72 which works out correctly to 25/72.
My math may be correct as in the answer is correct for my statements. But obviously I have made an error in the statements I have used.
Thanks once again for your help.
Because there are many methods to "count the ways" that allows for many ways to also get a wrong answer.Quote: CmdrBondMy math may be correct as in the answer is correct for my statements. But obviously I have made an error in the statements I have used.
Thanks once again for your help.
This is the text file I was looking for.
I had the formula in Excel but I could not find where it came from
http://perl.plover.com/misc/enumeration/enumeration.txt
The very last section talks why the math works.
Now you also want red/black colors (not to mention 6 suits making a total of 36 different faces)
so a pattern like one pair AABCDE
can also be either
ArArBCDE
AbAbBCDE
these two having the same number of ways to appear
and
ArAbBCDE
AbArBCDE
My method for these still works well but I now have to divide out the 2! ways ArAr and AbAb as the order of these do not matter
BCDE remains the same
maybe later if I get interested in it again
Have fun!
Sally
Quote: CmdrBondYou guys are brilliant. I might start to be able to get a handle on this now.
You say the rest of my math is OK, but there is still a discrepancy.
The total number of distinct 2 pairs is 25/72 (50/144).
The numbers I got for 2 distinct matched pair, 2 distinct mixed pair and 2 distinct pair where 1 is mixed and 1 is matched are
5/48, 5/36 and 5/72 or 15/144, 20/144 and 10/144 which totals 45/144.
According to the guys at BoardGameGeek, it should be 5/36, 5/36 and 5/72 which works out correctly to 25/72.
My math may be correct as in the answer is correct for my statements. But obviously I have made an error in the statements I have used.
Thanks once again for your help.
I get 5/36, 5/36, and 5/72 as well, but not in that order.
First, I don't like using permutations of the dice, but counting all 46,656 possible ways to roll the dice (as if three of the dice were different shades of red and the other three different shades of gray).
Divide the dice into two groups - Type R has "1" red, and Type B has "1" black. There are 3 of each type.
For two distinct pairs where both pairs match color, one pair must be two Type R dice, and the other must be two Type B dice. (A pair has to have the same type of dice in order to match, and if both pairs are of the same type, that's four dice of that type, but there are only three of each type being rolled.)
Out of all 46,656 possible rolls:
2 distinct matched pair have to be one pair from Type R dice and one pair from Type B
(otherwise you get four of some type, which is impossible as you only have three of each type)
There are 6 numbers for the Type R dice pair
There are 5 numbers for the Type B dice pair
There are 3 pairs of Type R dice that can be the Type R pair
There are 3 pairs of Type B dice that can be the Type B pair
There are 4 numbers that can be the remaining Type R die
There are 3 numbers that can be the remaining Type B die
Total = (6 x 5 x 3 x 3 x 4 x 3) / 46656 = 5/72
For the 2 distinct mixed pair, one die of each pair must be Type R and the other Type B (otherwise, they wouldn't be mixed).
There are 15 distinct pairs of numbers for the pairs
There are 3 dice that can be the Type R number of the higher pair
There are 3 dice that can be the Type B number of the higher pair
There are 2 dice that can be the Type R number of the lower pair
There are 2 dice that can be the Type B number of the lower pair
There are 4 numbers that can be the remaining Type R die
There are 3 numbers that can be the remaining Type B die
Total = (15 x 3 x 3 x 2 x 2 x 4 x 3) / 46656 = 5/36
For the 2 distinct mixed pair with one pair matched and one pair mixed, the mixed pair must have one of each type, and the matched pair must have two of the same type, so one type has all three dice in the pairs and the other type has one.
There are 6 numbers for the matched pair
There are 6 pairs of dice that can be the pair (3 pairs of type R; 3 pairs of type B)
There are 5 numbers for the mixed pair
There is 1 die from the same type as the matched pair that can be in the mixed pair
There are 3 dice from the other type that can be in the mixed pair
There are 6 pairs of numbers that can be used for the two unpaired dice
There are 2 dice that can be the higher of those two numbers
There is 1 die that can be the lower of those two
Total = (6 x 6 x 5 x 1 x 3 x 6 x 2 x 1) / 46656 = 5/36
using that same method I see where you have over-counted as did Don.Quote: CmdrBondI them came to those same results via a different angle
For any 2 distinct pairs (either matched or unmatched) and no other matching numbers.
6/6 - The 1st number can be anything.
1/6 - The 2nd number matches the first.
5/6 - The 3rd number does not match any previously rolled.
1/6 - The 4th number matches the 3rd.
4/6 - The 5th number does not match any previously rolled.
3/6 - The 6th number does not match any previously rolled.
15/1 - The number of ways the 1st pair can be arranged. C(6,2)
6/1 - the number of ways the 2nd pair can be arranged. C(4,2)6 x 1 x 5 x 1 x 4 x 3 x 15 x 6 32400 25 100
------------------------------ = ----- = -- = ---
6 x 6 x 6 x 6 x 6 x 6 x 1 x 1 46656 36 144
A A B B C D
6 1 5 1 4 3 = 360
6 6 6 6 6 6 = 46656
AA = 6C2 that leaves us with 4 dice remaining
BB = 4C2 that leaves us with 2 dice remaining
C = 2C1
D = 1C1
15*6*2*1 = 180
This is going from left to right
I can also go from right to left too
D=6C1 = 6
C= 5C1 = 5
BB=4C2 = 6
AA=2C2 = 1
6*5*6*1 = 180
But 360*180 is higher than 46656
I have over-counted the number of patterns for pairs and singles
AABB = BBAA but I counted them as two different ways
so I must divide out 2! for the 2 pairs and also the 2! for the singles
180/2!*2! = 45
now
360/46656 *45 = 16200/46656
now for the colors and the suits
Hoping to see your completed work soon
Sally
Quote: mustangsallyusing that same method I see where you have over-counted as did Don
Where did I overcount? I got the same numbers that appeared on BoardGameGeeks
There are 15 possible pairs of digits for the two pairs (1s and 2s, 1s and 3s,..., 4s and 6s, 5s and 6s)
For each one, there are 15 pairs of dice that the higher-numbered pair can be
There are 6 pairs of the remaining 4 dice that the lower-numbered pair can be
There are 12 sets of the remaining 4 numbers that can be on the remaining 2 dice
15 x 15 x 6 x 12 / 46656 = 25/72 = 5/36 + 5/36 + 5/72
Oops. You did not over-count.Quote: ThatDonGuyWhere did I overcount? I got the same numbers that appeared on BoardGameGeeks
That was worded poorly.
using that same method I see where you (OP) have over-counted as Don did also point out
https://wizardofvegas.com/forum/questions-and-answers/math/17924-dice-odds-for-unique-dice/#post352319
I like the use of your last method in calculating the 2 pair probabilities.
We have shown about 4 of them now.
Is there really a method that can prove one answer is correct over another that is not correct,
other than a full list and counting
Sally
Quote: TomspurWhat would this forum do without it's resident funny man :)
You mean Evenbob, I assume !
I've used formulae to build a table that lists every potential roll.
Finding pairs (and only) pairs is rough, but I've found that by testing for pair, triple, quad, quint and sext that I am able to A)add the "triple + pair" and "quad + pair" results then use those to eliminate the pairs that coincide with triples & quads.
Finding two pair/three pair is also going to be a challenge.
So far, I've got:
46656 potential combinations
36540 pairs (includes pairs that would be part of any combination)
14700 triples (count of single triples, would include those that are part of a double-triple as well)
2250 quads (regardless of the 2/2 or 3/1 color combo)
180 quints
6 sexts
7200 Triple + Pair (Full House?)
450 Quad + Pair
If you'd like the spreadsheet, let me know. I can post a link easily enough.
ETA:
28800 combinations with at least one pair that are not part of a triple+pair or quad+pair combo.
I use a different program to list all the possible permutations and then import that into ExcelQuote: TerribleTomIf nothing else, you've given me a tremendous Excel riddle.
I've used formulae to build a table that lists every potential roll.
Just takes about 1 minute
The fun part then begins with the counting.
doing it by hand is a "so far" processQuote: TerribleTomSo far, I've got:
That is why having a complete formula that the computer can use to calculate these are big time savers.
I need time to adjust mine for the colors and suits the OP really wants
still, who is correct and who is not is the final question for any pattern
ABCDEF is very simple
these two patterns
AAABCD: 1 trip and 3 singles: 7200
AAABBC: 1 trip, 1 pair and 1 single: 7200
they each have the same # of ways to appear?
how to prove this easily??
I just count them in Excel like you do and sure enough
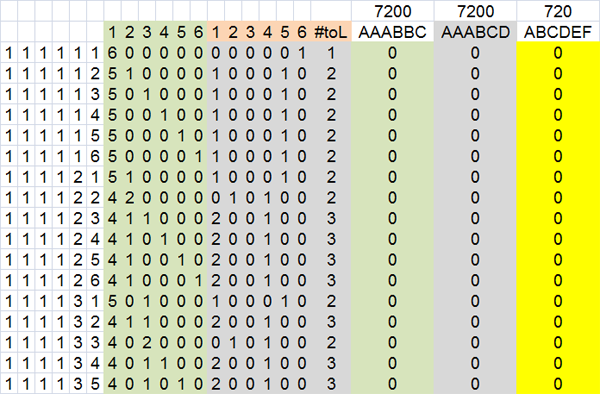
But did I count them correctly?
A proof is challenging IMO
I can do this a different way but is it correct?
I can say it must be because it is correct when used on less number of dice that can easily be counted.
AAABCD = 6C4*4! (this is the formula for replacing 6/6*1/6*1/6*5/6*4/6*3/6) = 360
this places the # of pips to the symbols (the letters)
now we have to place the number of letters to actual dice
That can be done in a few different ways too.
I use 6C3*3C1*2C1*1C1/3!(The 3 singles) = 20*3*2*1/3*2*1 = 20
360*20=7200
AAABBC = 6C3*3! = 120
6C3*3C2*1C1 = 20*3*1 = 60
60*120=7200
Of course, I just have Excel do this for me
Sally
1 REM DEFINE DICE TYPE X
2 DIM X$(6)
3 X$(1)="1r"
4 X$(2)="2b"
5 X$(3)="3r"
6 X$(4)="4b"
7 X$(5)="5r"
8 X$(6)="6b"
9
10 REM DEFINE DICE TYPE Y
11 DIM Y$(6)
12 Y$(1)="1b"
13 Y$(2)="2r"
14 Y$(3)="3b"
15 Y$(4)="4r"
16 Y$(5)="5b"
17 Y$(6)="6r"
18
19
20 REM SET DICE FACES AND ROLL COUNTER
21 LET A=1
22 LET B=1
23 LET C=1
24 LET D=1
25 LET E=1
26 LET F=1
27 LET R=0
28
29
30 REM ROLL THE DICE
31 LET R=R+1
32 PRINT X$(F),X$(E),X$(D),Y$(C),Y$(B),Y$(A),"ROLL ";R
33
34
35 REM INDEX THE ROLLS
36 LET A=A+1
37 IF A<7 GOTO 30
38 LET A=1
39
40 LET B=B+1
41 IF B<7 GOTO 30
42 LET B=1
43
44
45 LET C=C+1
46 IF C<7 GOTO 30
47 LET C=1
48
49
50 LET D=D+1
51 IF D<7 GOTO 30
52 LET D=1
53
54
55 LET E=E+1
56 IF E<7 GOTO 30
57 LET E=1
58
59
60 LET F=F+1
61 IF F<7 GOTO 30
62
63
64
65 END
If you want to try it, go toand just copy/paste it into the right window and hit start.
Takes about 5 minutes to complete :D
Now - how to work out how to count the groupings?
Might have to look at converting that into vbasic or some more modern language first, then look at expanding the variables and setting 2 variables for each face then using some kind of script to compare them - I have some ideas on this, but I think I need to convert languages first.
6 different numbers order counts: p(6,6)=720
All red:
3 choices for die 1, 2 for die 2 , 1 for die 3, 3 for die 4 ,2 for die 5,and 1 for die 6:
3*2*1*3*2*1
All black:
same as all red
Total all same color:
2*3*2*1*3*2*1=72
6 choices for AA = 6
c(6,2)= 15 positions for AA
choose 4 of 5 numbers order counts for BCDE: p(5,4)= 120
6*15*120=10800
Red AA both 1:
choose 2 of 3 positions c(3,2)=3
choose 4 of 5 numbers order counts for BCDE: p(5,4)= 120
3*120=360
AA same color:
Repeat for Black AA and for each number: 2 * 6
2*6*360=4320
c(6,2)=15 choices for AA and BB
c(6,2)=15 positions for AA
c(4,2)=6 positions for BB
choose 2 of 4 numbers order counts for BCDE: p(4,2)= 12
15*15*6*12=16200
1 and 2 for A and B ( all 9 odd and even pairs):
All same color:
2 color choices
c(3,2)=3 positions for 1
c(3,2)=3 positions for 2
2*3*3=18 (162)
Both mixed color:
3 for red1 and 2 for black2
3 for black1 and 2 for red2
2*3*2*3=36 (324)
One matched and one mixed:
2 color choices for matched (red or black)
2 number choices for matched (1 or 2)
c(3,2)=3 positions for matched
1 position for mixed in the color of matched
3 positions for mixed in opposite matched color
2*2*3*1*3=36 (324)
1 and 3 for A and B ( all 6 both odd or both even pairs):
One matched and one mixed:
2 color choices for matched (red or black)
2 number choices for matched (1 or 2)
c(3,2)=3 positions for matched
1 position for mixed in the color of matched
3 positions for mixed in opposite matched color
2*2*3*1*3=36 (216)
Both mixed color:
3 for red1 and 2 for black3
3 for black1 and 2 for red3
2*3*2*3=36 (216)
Both matched(different colors):
2 color choices for 1
c(3,2)=3 positions for 1
c(3,2)=3 positions for 3
2*3*3=18 (108)
Summery (*p(4,2) for the last 2 dice):
All same color: 162 (1944)
Both matched(different colors): 108 (1296)
Both Mixed: 540 (6480)
One Matched One Mixed: 540 (6480)
c(6,3)=20 choices the numbers
c(6,2)=15 positions for AA
c(4,2)=6 positions for BB
20*15*6=1800
2 (AA and BB) matched 1 mixed (CC):
c(3,2)=3 positions for AA
c(3,2)=3 positions for BB
6 numbers for AA
5 numbers for BB (3 will be the same color, 2 different)
4 numbers for CC
3*3*6*5*4 = 1080 (648 same color, 432 different colors)
3 mixed:
c(6,3)=20 choices the numbers
3*3 positions for AA
2*2 positions for BB
20*3*3*2*2=720
6 choices for AAA = 6
c(6,3)= 20 positions for AAA
choose 3 of 5 numbers order counts for BCDE: p(5,3)= 60
6*20*60 = 7200
Matched:
6 choices for AAA = 6
2 positions for AAA
choose 3 of 5 numbers order counts for BCDE: p(5,3)= 60
6*2*60 = 720
Mixxed
6 choices for AAA = 6
c(6,3)-2=18 positions for AAA
choose 3 of 5 numbers order counts for BCDE: p(5,3)= 60
6*18*60 = 6480
6 choices for AAA = 6
c(6,3)= 20 positions for AAA
5 choices for BB = 5
c(3,2)= 3 positions for BB
4 choices for C
6*20*5*3*4=7200
AAABB all same color:
6 choices for AAA = 6
2 positions for AAA
3 choices for BB
c(3,2)= 3 positions for BB
4 choices for C
6*2*3*3*4=432
AAA color BB opposite color:
6 choices for AAA = 6
2 positions for AAA
2 choices for BB
c(3,2)= 3 positions for BB
4 choices for C
6*2*2*3*4=288
AAA Mixed, BB color, both odd or both even
6 choices for BB
2 color choices for BB
c(3,2)=3 position for BB
2 choices for AAA
c(3,2)=3 positions for AAA
4 choices for C
6*2*3*2*3*4= 864
AAA Mixed, BB color, one odd one even:
6 choices for BB
2 color choices for BB
c(3,2)=3 position for BB
3 choices for AAA
c(3,2)=3 positions for AAA
4 choices for C
6*2*3*3*3*4= 1296
AAA Mixed BB Mixed:
6 choices for BB
3*3=9 positions for BB
5 choices for AAA
c(4,3)=4 positions for AAA
4 choices for C
6*9*5*4*4=4320
c(6,2)=15 number choices
c(6,3)=20 positions
15*20 = 300
all same color:
6 number choices on dice 1-3
3 number choices on dice 4-6
6*3=18
AAA one color and BBB another:
6 number choices on dice 1-3
2 number choices on dice 4-6
6*2=12
AAA and BBB both mixed:
6 number choices for die 1
either 1 of 2 from dice 2-3 and 1 from dice 4-6 2*3 or both from dice 4-6 c(3,2)=3
5 number choices for remaining 3 dice
6*(2*3 + 3)*5=270
6 number choices for A
c(6,4)=15 positions for A
choose 2 of 5 numbers order counts for BC: p(5,2)= 20
6*15*20=1800
2 of each color for AAAA:
6 number choices for A
c(3,2)=3 positions for red A
c(3,2)=3 positions for black A
choose 2 of 5 numbers order counts for BC: p(5,2)= 20
6*3*3*20 = 1080
3 of 1 color and 1 of the other for AAAA:
6 number choices
2 color choices
3 positions for single color
choose 2 of 5 numbers order counts for BC: p(5,2)= 20
6*2*3*20=720
6 number choices for A
c(6,4)=15 positions for A
5 number choices for B
6*15*5=450
2 of each color for AAAA (BB will be mixed):
6 number choices for A
c(3,2)=3 positions for red A
c(3,2)=3 positions for black A
5 number choices for B
6*3*3*5 = 270
3 of 1 color and 1 of the other for AAAA (BB will be Matched):
6 number choices
2 color choices
3 positions for single color
5 number choices for B
6*2*3*5=180
6 number choices for A
5 number choicse for B
6 positions for B
6*5*6=180
The square root of 36 is 6, but why did you click on this spoiler?
I like your (Sally) count column strategy.
google doc spread sheet
Edit to add: I made a copy that uses named ranges instead of "Sheet2!X3:X46658" everywhere so it might make it easier to understand.
googledoc with named ranges
I've still got my programming head on :D
I have successfully created a program that now rolls all 46656 combinations AND records all the variant hands for 6 standard dice.
pop over toand paste it into the Qloud to test it.
DIM FACE(5)
FOR DIE = 0 TO 5
READ FACE(DIE)
DATA 1,1,1,1,1,1
NEXT DIE
LET ROLL = 0
DIM HANDS(10)
FOR HAND = 0 TO 9
READ HANDS(HAND)
DATA 0,0,0,0,0,0,0,0,0,0
NEXT HAND
DIM COUNT(6)
roll:
FOR THROW = 1 TO 6
RESTORE dataY
FOR POSITION = 0 TO 6
READ COUNT(POSITION)
dataY:
DATA 0,0,0,0,0,0,0
NEXT POSITION
FOR RESULT = 1 TO 6
LET TALLY = 0
FOR SPOTS = 0 TO 5
IF FACE(SPOTS) = RESULT THEN LET TALLY = TALLY + 1
NEXT SPOTS
LET COUNT(TALLY) = COUNT(TALLY) + 1
NEXT RESULT
NEXT THROW
IF COUNT(2) = 1 AND COUNT(3) = 0 AND COUNT(4) = 0 THEN LET HANDS(0) = HANDS(0) + 1
IF COUNT(2) = 2 THEN LET HANDS(1) = HANDS(1) + 1
IF COUNT(2) = 3 THEN LET HANDS(2) = HANDS(2) + 1
IF COUNT(3) = 1 AND COUNT(2) = 0 THEN LET HANDS(3) = HANDS(3) + 1
IF COUNT(3) = 1 AND COUNT(2) = 1 THEN LET HANDS(4) = HANDS(4) + 1
IF COUNT(3) = 2 THEN LET HANDS(5) = HANDS(5) + 1
IF COUNT(4) = 1 AND COUNT(2) = 0 THEN LET HANDS(6) = HANDS(6) + 1
IF COUNT(4) = 1 AND COUNT(2) = 1 THEN LET HANDS(7) = HANDS(7) + 1
IF COUNT(5) = 1 THEN LET HANDS(8) = HANDS(8) + 1
IF COUNT(6) = 1 THEN LET HANDS(9) = HANDS(9) + 1
LET ROLL = ROLL + 1
PRINT FACE(0); " - "; FACE(1); " - "; FACE(2); " - "; FACE(3); " - "; FACE(4); " - "; FACE(5),_
ROLL, COUNT(6); COUNT(5); COUNT(4); COUNT(3); COUNT(2)
LET FACE(5) = FACE(5) + 1
IF FACE(5) < 7 THEN GOTO roll ELSE LET FACE(5) = 1
LET FACE(4) = FACE(4) + 1
IF FACE(4) < 7 THEN GOTO roll ELSE LET FACE(4) = 1
LET FACE(3) = FACE(3) + 1
IF FACE(3) < 7 THEN GOTO roll ELSE LET FACE(3) = 1
LET FACE(2) = FACE(2) + 1
IF FACE(2) < 7 THEN GOTO roll ELSE LET FACE(2) = 1
LET FACE(1) = FACE(1) + 1
IF FACE(1) < 7 THEN GOTO roll ELSE LET FACE(1) = 1
LET FACE(0) = FACE(0) + 1
IF FACE(0) < 7 THEN GOTO roll ELSE LET FACE(0) = 1
PRINT "TOTAL NUMBER OF HANDS CONTAINING"
PRINT "1 PAIR:", HANDS(0)
PRINT "2 PAIRS:", HANDS(1)
PRINT "3 PAIRS:", HANDS(2)
PRINT "1 TRIP:", HANDS(3)
PRINT "1 TRIP/1 PAIR:"; HANDS(4)
PRINT "2 TRIPS:", HANDS(5)
PRINT "1 QUAD:", HANDS(6)
PRINT "1 QUAD/1 PAIR:"; HANDS(7)
PRINT "1 QUINT:", HANDS(8)
PRINT "1 SEXTUPLE:", HANDS(9)
the result is this
1 - 1 - 1 - 1 - 1 - 1 1 1 0 0 0 0
1 - 1 - 1 - 1 - 1 - 2 2 0 1 0 0 0
1 - 1 - 1 - 1 - 1 - 3 3 0 1 0 0 0
1 - 1 - 1 - 1 - 1 - 4 4 0 1 0 0 0
1 - 1 - 1 - 1 - 1 - 5 5 0 1 0 0 0
1 - 1 - 1 - 1 - 1 - 6 6 0 1 0 0 0
1 - 1 - 1 - 1 - 2 - 1 7 0 1 0 0 0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
6 - 6 - 6 - 6 - 6 - 6 46656 1 0 0 0 0
TOTAL NUMBER OF HANDS CONTAINING
1 PAIR: 10800
2 PAIRS: 16200
3 PAIRS: 1800
1 TRIP: 7200
1 TRIP/1 PAIR: 7200
2 TRIPS: 300
1 QUAD: 1800
1 QUAD/1 PAIR: 450
1 QUINT: 180
1 SEXTUPLE: 6
Where the numbers on the left indicate the dice face, the centre the roll number and the right the number of matching dice (in the order 6's, 5's, 4's, 3's & 2's)
Here is my final program - once again pop it into(or even better pop qb64 on your machine - it runs better)
start_time = TIMER
OUT &H3C8, 0 'Set COLOR 0 to black
OUT &H3C9, 1 'R%
OUT &H3C9, 1 'G%
OUT &H3C9, 1 'B%
OUT &H3C8, 1 'set COLOR 1 to red
OUT &H3C9, 63 'R%
OUT &H3C9, 1 'G%
OUT &H3C9, 1 'B%
OUT &H3C8, 2 'set COLOR 2 to white
OUT &H3C9, 63 'R%
OUT &H3C9, 63 'G%
OUT &H3C9, 63 'B%
OUT &H3C8, 3 'set COLOR 3 to dark green
OUT &H3C9, 1 'R%
OUT &H3C9, 19 'G%
OUT &H3C9, 1 'B%
COLOR 2, 3 'Set forground (text) colour to white and background colour to dark green
CLS
DIM face(6)
DIM count_spots(6)
DIM colour(6)
DIM r(6)
DIM b(6)
DIM sr(6)
DIM sb(6)
roll = 0
one_pair = 0: xx = 0: xy = 0
two_pair = 0: xx_xx = 0: xx_yy = 0: xx_xy = 0: xy_xy = 0
three_pair = 0: xx_xx_xy = 0: xx_yy_xy = 0: xy_xy_xy = 0
one_trip = 0: xxx = 0: xxy = 0
one_trip_one_pair = 0: xxx_xx = 0: xxx_yy = 0: xxy_xx = 0: xxy_yy = 0: xxy_xy = 0
two_trips = 0: xxx_xxx = 0: xxx_yyy = 0: xxx_xxy = 0: xxy_xxy = 0
one_quad = 0: xxxy = 0: xxyy = 0
one_quad_one_pair = 0: xxxy_xx = 0: xxxy_yy = 0: xxxy_xy = 0: xxyy_xx = 0: xxyy_xy = 0
one_quint = 0
one_sextuple = 0
one_straight = 0: xxxxxx = 0: xxxxyy = 0: xxxyyy = 0
FOR die = 1 TO 6
face(die) = 1
NEXT die
PRINT " NO. SHOWING ON | ROLL | NO. OF GROUPS OF | COLOUR OF FACE"
PRINT " THE DICE FACE | NO. | 6 5 4 3 2 1 | RED=1 BLACK=0"
PRINT "------------------+-------+------------------+-----------------"
roll: 'GOTO roll returns here
FOR position = 1 TO 6
colour(position) = (face(position) + ((position - 1) \ 3)) MOD 2
count_spots(position) = 0
group(position) = 0
r(position) = 0
b(position) = 0
sr(position) = 0
sb(position) = 0
NEXT position
g = 0
sg = 0
FOR dice = 1 TO 6
tally_spots = 0
tally_red = 0
tally_black = 0
FOR spots = 1 TO 6
IF face(spots) = dice THEN
tally_spots = tally_spots + 1
IF colour(spots) = 1 THEN
tally_red = tally_red + 1
ELSEIF colour(spots) = 0 THEN
tally_black = tally_black + 1
END IF
END IF
NEXT spots
IF tally_spots > 1 THEN
count_spots(tally_spots) = count_spots(tally_spots) + 1
g = g + 1
r(g) = r(g) + tally_red
b(g) = b(g) + tally_black
ELSEIF tally_spots = 1 THEN
count_spots(tally_spots) = count_spots(tally_spots) + 1
sg = sg + 1
sr(sg) = sr(sg) + tally_red
sb(sg) = sb(sg) + tally_black
END IF
NEXT dice
IF count_spots(2) = 1 AND count_spots(3) = 0 AND count_spots(4) = 0 THEN
one_pair = one_pair + 1
IF r(1) = 2 OR b(1) = 2 THEN
xx = xx + 1
ELSE
xy = xy + 1
END IF
ELSEIF count_spots(2) = 2 THEN
two_pair = two_pair + 1
IF r(1) + r(2) = 4 OR b(1) + b(2) = 4 THEN
xx_xx = xx_xx + 1
ELSEIF r(1) + r(2) = 3 OR b(1) + b(2) = 3 THEN
xx_xy = xx_xy + 1
ELSEIF r(1) = 1 AND r(2) = 1 AND b(1) = 1 AND b(2) = 1 THEN
xy_xy = xy_xy + 1
ELSE
xx_yy = xx_yy + 1
END IF
ELSEIF count_spots(2) = 3 THEN
three_pair = three_pair + 1
IF r(1) + r(2) + r(3) = 5 OR b(1) + b(2) + b(3) = 5 THEN
xx_xx_xy = xx_xx_xy + 1
ELSEIF r(1) = 1 AND r(2) = 1 AND r(3) = 1 AND b(1) = 1 AND b(2) = 1 AND b(3) = 1 THEN
xy_xy_xy = xy_xy_xy + 1
ELSE
xx_yy_xy = xx_yy_xy + 1
END IF
ELSEIF count_spots(3) = 1 AND count_spots(2) = 0 THEN
one_trip = one_trip + 1
IF r(1) = 3 OR b(1) = 3 THEN
xxx = xxx + 1
ELSE
xxy = xxy + 1
END IF
ELSEIF count_spots(3) = 1 AND count_spots(2) = 1 THEN
one_trip_one_pair = one_trip_one_pair + 1
IF r(1) + r(2) = 5 OR b(1) + b(2) = 5 THEN
xxx_xx = xxx_xx + 1
ELSEIF r(1) + b(2) = 5 OR r(2) + b(1) = 5 THEN
xxx_yy = xxx_yy + 1
ELSEIF (r(1) = 2 AND b(1) = 1 AND r(2) = 2) OR (r(1) = 1 AND b(1) = 2 AND b(2) = 2)_
OR (r(1) = 2 AND r(2) = 2 AND b(2) = 1) OR (b(1) = 2 AND r(2) = 1 AND b(2) = 2) THEN
xxy_xx = xxy_xx + 1
ELSEIF (r(1) = 2 AND b(1) = 1 AND b(2) = 2) OR (r(1) = 1 AND b(1) = 2 AND r(2) = 2)_
OR (r(1) = 2 AND r(2) = 1 AND b(2) = 2) OR (b(1) = 2 AND r(2) = 2 AND b(2) = 1) THEN
xxy_yy = xxy_yy + 1
ELSEIF ((r(1) = 2 AND b(1) = 1) OR (r(1) = 1 AND b(1) = 2)) AND (r(2) = 1 AND b(2) = 1)_
OR (r(1) = 1 AND b(1) = 1) AND ((r(2) = 2 AND b(2) = 1) OR (r(2) = 1 AND b(2) = 2)) THEN
xxy_xy = xxy_xy + 1
END IF
ELSEIF count_spots(3) = 2 THEN
two_trips = two_trips + 1
IF r(1) + r(2) = 6 OR b(1) + b(2) = 6 THEN
xxx_xxx = xxx_xxx + 1
ELSEIF r(1) + b(2) = 6 OR r(2) + b(1) = 6 THEN
xxx_yyy = xxx_yyy + 1
ELSEIF r(1) < 3 AND r(2) < 3 AND b(1) < 3 AND b(2) < 3 THEN
xxy_xyy = xxy_xyy + 1
END IF
ELSEIF count_spots(4) = 1 AND count_spots(2) = 0 THEN
one_quad = one_quad + 1
IF r(1) = 3 OR b(1) = 3 THEN
xxxy = xxxy + 1
ELSEIF r(1) = 2 AND b(1) = 2 THEN
xxyy = xxyy + 1
END IF
ELSEIF count_spots(4) = 1 AND count_spots(2) = 1 THEN
one_quad_one_pair = one_quad_one_pair + 1
IF (r(1) = 3 AND r(2) = 2) OR (r(1) = 2 AND r(2) = 3) OR (b(1) = 3 AND b(2) = 2) OR (b(1) = 2 AND b(2) = 3) THEN
xxxy_xx = xxxy_xx + 1
ELSEIF (r(1) = 3 AND b(2) = 2) OR (r(1) = 2 AND b(2) = 3) OR (b(1) = 3 AND r(2) = 2) OR (b(1) = 2 AND r(2) = 3) THEN
xxxy_yy = xxxy_yy + 1
ELSEIF ((r(1) = 3 AND b(1) = 1) OR (r(1) = 1 AND b(1) = 3)) AND (r(2) = 1 AND b(2) = 1)_
OR ((r(2) = 3 AND b(2) = 1) OR (r(2) = 1 AND b(2) = 3)) AND (r(1) = 1 AND b(1) = 1) THEN
xxxy_xy = xxxy_xy + 1
ELSEIF (r(1) = 1 AND r(2) = 2) OR (b(1) = 2 AND b(2) = 2) THEN
xxyy_xx = xxyy_xx + 1
ELSEIF (r(1) = 2 AND b(1) = 2 AND r(2) = 1 AND b(2) = 1) OR (r(1) = 1 AND b(1) = 1 AND r(2) = 2 AND b(2) = 2) THEN
xxyy_xy = xxyy_xy + 1
END IF
ELSEIF count_spots(5) = 1 THEN
one_quint = one_quint + 1
ELSEIF count_spots(6) = 1 THEN
one_sextuple = one_sextuple + 1
ELSEIF count_spots(1) = 6 THEN
one_straight = one_straight + 1
IF sr(1) + sr(2) + sr(3) + sr(4) + sr(5) + sr(6) = 6 OR sb(1) + sb(2) + sb(3) + sb(4) + sb(5) + sb(6) = 6 THEN
xxxxxx = xxxxxx + 1
ELSEIF sr(1) + sr(2) + sr(3) + sr(4) + sr(5) + sr(6) = 4 OR sb(1) + sb(2) + sb(3) + sb(4) + sb(5) + sb(6) = 4 THEN
xxxxyy = xxxxyy + 1
END IF
END IF
LET roll = roll + 1
FOR throw_spots = 1 TO 6
COLOR colour(throw_spots): PRINT face(throw_spots);
NEXT throw_spots
COLOR 2: PRINT "|";
IF roll < 10 THEN
PRINT " "; roll;
ELSEIF roll < 100 THEN
PRINT " "; roll;
ELSEIF roll < 1000 THEN
PRINT " "; roll;
ELSEIF roll < 10000 THEN
PRINT " "; roll;
ELSE
PRINT roll;
END IF
PRINT "|"; count_spots(6); count_spots(5); count_spots(4); count_spots(3); count_spots(2); count_spots(1); "|";
FOR throw_colour = 1 TO 6
COLOR colour(throw_colour): PRINT colour(throw_colour);
NEXT throw_colour
COLOR 2: PRINT " "
face(6) = face(6) + 1
IF face(6) < 7 THEN
GOTO roll
ELSE
face(6) = 1
face(5) = face(5) + 1
IF face(5) < 7 THEN
GOTO roll
ELSE
face(5) = 1
face(4) = face(4) + 1
IF face(4) < 7 THEN
GOTO roll
ELSE
face(4) = 1
face(3) = face(3) + 1
IF face(3) < 7 THEN
GOTO roll
ELSE
face(3) = 1
face(2) = face(2) + 1
IF face(2) < 7 THEN
GOTO roll
ELSE
face(2) = 1
face(1) = face(1) + 1
IF face(1) < 7 THEN
GOTO roll
ELSE
face(1) = 1
END IF
END IF
END IF
END IF
END IF
END IF
PRINT "TOTAL NUMBER OF HANDS CONTAINING"
PRINT "1 PAIR:", one_pair; "- XX:"; xx; "- XY:"; xy
PRINT "2 PAIRS:", two_pair; "- XX XX:"; xx_xx; "- XX YY:"; xx_yy; "- XX XY:"; xx_xy; "- XY XY:"; xy_xy
PRINT "3 PAIRS:", " "; three_pair; "- XX XX XY:"; xx_xx_xy; "- XX YY XY:"; xx_yy_xy; "- XY XY XY:"; xy_xy_xy
PRINT "1 TRIP:", " "; one_trip; "- XXX:"; xxx; "- XXY:"; xxy
PRINT "1 TRIP/1 PAIR:"; " "; one_trip_one_pair; "- XXX XX:"; xxx_xx; "- XXX YY:"; xxx_yy; "- XXY XX:"; xxy_xx
PRINT " ", " "; "XXY YY:"; xxy_yy; "- XXY XY:"; xxy_xy
PRINT "2 TRIPS:", " "; two_trips; "- XXX XXX:"; xxx_xxx; "- XXX YYY"; xxx_yyy; "- XXY XYY:"; xxy_xyy
PRINT "1 QUAD:", " "; one_quad; "- XXXY:"; xxxy; "- XXYY"; xxyy
PRINT "1 QUAD/1 PAIR:"; " "; one_quad_one_pair; "- XXXY XX:"; xxxy_xx; "- XXXY YY:"; xxxy_yy; "- XXYY_XX:"; xxyy_xx; "- XXYY XY:"; xxyy_xy
PRINT "1 QUINT:", " "; one_quint; "- XXXYY:"; one_quint
PRINT "1 SEXTUPLE:", " "; one_sextuple; "- XXXYYY:"; one_sextuple
PRINT "1 STRAIGHT:", " "; one_straight; "- XXXXXX:"; xxxxxx; "- XXXXYY:"; xxxxyy
end_time = TIMER
PRINT "This program took "; end_time - start_time; " seconds to execute"
FOR reset_COLOR = 1 TO 256
OUT &H3C7, reset_COLOR
R% = INP(&H3C9)
G% = INP(&H3C9)
B% = INP(&H3C9)
NEXT reset_COLOR
And this gives the following results (expanding only slightly on Miplet's wonderful spreadsheets)
NO. SHOWING ON | ROLL | NO. OF GROUPS OF | COLOUR OF FACE
THE DICE FACE | NO. | 6 5 4 3 2 1 | RED=1 BLACK=0
------------------+-------+------------------+-----------------
1 1 1 1 1 1 | 1 | 1 0 0 0 0 0 | 1 1 1 0 0 0
1 1 1 1 1 2 | 2 | 0 1 0 0 0 1 | 1 1 1 0 0 1
1 1 1 1 1 3 | 3 | 0 1 0 0 0 1 | 1 1 1 0 0 0
1 1 1 1 1 4 | 4 | 0 1 0 0 0 1 | 1 1 1 0 0 1
1 1 1 1 1 5 | 5 | 0 1 0 0 0 1 | 1 1 1 0 0 0
1 1 1 1 1 6 | 6 | 0 1 0 0 0 1 | 1 1 1 0 0 1
1 1 1 1 2 1 | 7 | 0 1 0 0 0 1 | 1 1 1 0 1 0
...
6 6 6 6 6 1 | 46651 | 0 1 0 0 0 1 | 0 0 0 1 1 0
6 6 6 6 6 2 | 46652 | 0 1 0 0 0 1 | 0 0 0 1 1 1
6 6 6 6 6 3 | 46653 | 0 1 0 0 0 1 | 0 0 0 1 1 0
6 6 6 6 6 4 | 46654 | 0 1 0 0 0 1 | 0 0 0 1 1 1
6 6 6 6 6 5 | 46655 | 0 1 0 0 0 1 | 0 0 0 1 1 0
6 6 6 6 6 6 | 46656 | 1 0 0 0 0 0 | 0 0 0 1 1 1
1 PAIR: 10800 - XX: 4320 - XY: 6480
2 PAIRS: 16200 - XX XX: 1944 - XX YY: 1296 - XX XY: 6480 - XY XY: 6480
3 PAIRS: 1800 - XX XX XY: 648 - XX YY XY: 432 - XY XY XY: 720
1 TRIP: 7200 - XXX: 720 - XXY: 6480
1 TRIP/1 PAIR: 7200 - XXX XX: 432 - XXX YY: 288 - XXY XX: 1296
XXY YY: 864 - XXY XY: 4320
2 TRIPS: 300 - XXX XXX: 18 - XXX YYY 12 - XXY XYY: 270
1 QUAD: 1800 - XXXY: 720 - XXYY 1080
1 QUAD/1 PAIR: 450 - XXXY XX: 108 - XXXY YY: 72 - XXYY_XX: 135 - XXYY XY: 135
1 QUINT: 180 - XXXYY: 180
1 SEXTUPLE: 6 - XXXYYY: 6
1 STRAIGHT: 720 - XXXXXX: 72 - XXXXYY: 648
This program took 43.40625 seconds to execute


