Wiz, ME, Sally - am I missing a relatively quick way of solving this mathematically? The fact that the number comes out to pretty much exactly 9/2 makes me think there's a better way to do this than brute forcing every string of rolls.
Quote: ThatDonGuyIf you include the repeat roll in your count (e.g. starting with a 6 and then immediately rolling another 6 is 2 rolls; 6, 11, 6 is 3), then I get exactly 4.5 by brute force (validated by a 1,000,000 roll Monte Carlo).
Wiz, ME, Sally - am I missing a relatively quick way of solving this mathematically? The fact that the number comes out to pretty much exactly 9/2 makes me think there's a better way to do this than brute forcing every string of rolls.
I am extremely offended that you didn't ask me. Plus I don't know the answer.
There are "only" 2^11 states here. However, there is symmetry there -- hitting a 2 on the first roll is the same state (probability-wise) as hitting a 12, so you can actually reduce this to 2x3^5 = 486 states.
At this point I would probably just bite the bullet and write a small program to go through all 486 states, since it will probably take less time than it would take me to find the simple solution, if one exists. I feel pretty confident that one does exist, and I will feel stupid for not seeing it when someone else points it out.
Quote: MathExtremistI'm not sure of the exact parameters here. Is it a repeat of the starting number? Any number that was rolled since the sequence started? Repeating consecutive numbers? The answer will be different for all 3 questions so which question are you asking here?
i think it's the second one. any number rolled since the sequence started. i can't think of an elegant solution to it.
Quote: chrisri can't think of an elegant solution to it.
If you look at then Wizard's pass or don't pass math in the craps section, this conclusion makes perfect sense.
http://en.wikipedia.org/wiki/Coupon_collector's_problem
The variant being "what is the mean time for drawing one coupon twice, with replacement, given a non-uniform distribution"?
Quote: MathExtremistI'm not sure of the exact parameters here. Is it a repeat of the starting number? Any number that was rolled since the sequence started? Repeating consecutive numbers? The answer will be different for all 3 questions so which question are you asking here?
The second one is what I meant - any number that was rolled since the sequence started. Thanks!
4.500070717 rolls on average.
Rolls Probability Roll*Probability
2 0.112654321 0.225308642
3 0.1967592593 0.5902777778
4 0.2258659122 0.9034636488
5 0.1990883631 0.9954418153
6 0.1395897766 0.8375386596
7 0.07790057701 0.5453040391
8 0.0339742293 0.2717938344
9 0.01116541789 0.100488761
10 0.002596243862 0.02596243862
11 0.0003796973656 0.004176671022
12 0.00002620245309 0.000314429437
Sum 1 4.500070717
(I'll format this table later tonight)
The odds of any given number coming up are 1/12.
Assuming the number does not repeat on the subsequent roll, the odds of either the first or second number coming up on a third roll would be 2/12 or 1/6.
After 12 rolls with no repeat, the odds of a repeat will be 1/1.
ETA - all occurrences of "12" above should be "11"
1/11
2/11 (not 1/6)
etc.
Quote: TerribleTomIs it possible we're over thinking this question?
The odds of any given number coming up are 1/12.
Huh?
Quote: AxiomOfChoiceHuh?
Sorry. I am retarded.
1 in 11.
2 in 11, etc.
OP seems unconcerned about what the starting number might be.
The answer is somewhere between 1 and 11, as the 11th roll after the initial roll will have to be a repeat of one of the previous numbers.
For a simple example, let's say the sequence goes like so:
2-3-4-5-6-7-8-9-10-11-12
The next number has a 1 in 1 chance of being a repeat of a prior number.
The odds of repeating any number with the next roll would be:
1 0.090909091
2 0.181818182
3 0.272727273
4 0.363636364
5 0.454545455
6 0.545454545
7 0.636363636
8 0.727272727
9 0.818181818
10 0.909090909
11 1
The average is the same as the 6th roll (.545454...repeating)
I'm going with the simple answer here. 6. The average number of rolls before any prior roll repeats is 6.
Quote: TerribleTomSorry. I am retarded.
1 in 11.
2 in 11, etc.
We are talking about rolling two dice here. All outcomes are not equally likely.
Quote: AxiomOfChoiceWe are talking about rolling two dice here. All outcomes are not equally likely.
True, but the original roll can also be any number. Right?
If one wanted to calculate the odds of a specific number being rolled a second time, that would be a whole different riddle.
Given "any number" and "any number" does that not simplify the equation?
ETA - when the rolls are "any number", "any number", "any number", "any number", "any number", "any number"...
Quote: TerribleTomTrue, but the original roll can also be any number. Right?
If one wanted to calculate the odds of a specific number being rolled a second time, that would be a whole different riddle.
Given "any number" and "any number" does that not simplify the equation?
No. The numbers are not all equally likely, so the more likely numbers are more likely to be rolled first, and be targets for repeats. As the distribution gets further away from being uniform, the average number of rolls before a repeat decreases.
Imagine if you were flipping a very biased coin where tails had only a 1-in-a-million chance of showing up. What is the average number of flips before a repeat? Compare to a fair coin.
Quote: AxiomOfChoiceNo. The numbers are not all equally likely, so the more likely numbers are more likely to be rolled first, and be targets for repeats. As the distribution gets further away from being uniform, the average number of rolls before a repeat decreases.
Imagine if you were flipping a very biased coin where tails had only a 1-in-a-million chance of showing up. What is the average number of flips before a repeat? Compare to a fair coin.
But that's just it. We don't know what *any* of the numbers are.
If the numbers are 6, 7, 8, the odds that roll #4 is a repeat are much higher than if they were 2, 3, 12.
Roll 1 = any number (1 in 11)
Roll 2 = not a repeat of 1 (10 in 11)
Roll 3 = not a repeat of 1 or 2 (9 in 11)
...
Roll 11 = not a repeat of the prior 10 (1 in 11)
Roll 12 = 1 in 1, the result must be a repeat.
Since you are denied the knowledge of any specific number, it's impossible to be precise.
Quote: TerribleTomBut that's just it. We don't know what *any* of the numbers are.
If the numbers are 6, 7, 8, the odds that roll #4 is a repeat are much higher than if they were 2, 3, 12.
Roll 1 = any number (1 in 11)
Roll 2 = not a repeat of 1 (10 in 11)
Roll 3 = not a repeat of 1 or 2 (9 in 11)
...
Roll 11 = not a repeat of the prior 10 (1 in 11)
Roll 12 = 1 in 1, the result must be a repeat.
Since you are denied the knowledge of any specific number, it's impossible to be precise.
No it's not. You know the probability distribution for every roll.
If you know what the rolls are it is easy to figure. When you don't know what any of the rolls are...
I like how he just brute forced his way to an answer.
Quote: TerribleTomOk. So you have this bell curve from 2 to 12 with a peak at 7 for every roll. Without knowing where on that bell curve you start, how do you calculate an average number of rolls for potential dupes?
If you know what the rolls are it is easy to figure. When you don't know what any of the rolls are...
These is no bell curve. The probabilities are all discrete.
It's all just a weighted average. You can calculate the exact probability of any sequence of rolls. There are only finitely many possible sequences (as you pointed out, the max length is 12) so you can literally take the weighted average of the length of each series (weighted by probability, of course). It's a finite sum so you don't need to worry about convergence or anything; just add up all the numbers and you are done.
The question being posed here, is, is there a nice solution to the problem (ie, not simulation or brute force)
Quote: chrisrthe answer is ~4.5007, not exactly 9/2. nicely done.
Does this conclusion allow for roundoff error in the calculation?
It may take some major Bignum crunching to come up with an exact answer.
Quote: ThatDonGuyDoes this conclusion allow for roundoff error in the calculation?
It may take some major Bignum crunching to come up with an exact answer.
I'll do an exact answer later (I'll have to write a program instead of using a spreadsheet), but I don't think its exactly 9/2. I get 4.50007071708602 which is as many decimals as google docs (see link on page 2) have.
33060401261 / (27 * 272097792)
which is 4.50007072
That the answer is so close to 4.5 is certainly convenient. It's pretty easy to remember "four and a half ”.
Quote: TerribleTomThat looks like it's probably the simplest solution possible.
The denominator is 29 x 315, and the numerator is not a multiple of 2 or 3, so the fraction cannot be reduced further.
Quote: ThatDonGuyHere's the exact answer:
33060401261 / (27 * 272097792)
which is 4.50007072
im not sure that is correct.. there is a more exact answer i think..excel gets further than the 7072.. i think it even rounds though at some point probally need more than i32s
Quote: chrisrim not sure that is correct.. there is a more exact answer i think..excel gets further than the 7072.. i think it even rounds though at some point probally need more than i32s
I just confirmed that the exact answer is 33060401261 / (27 * 272097792). You can use wolfram-alpha to get as many digits as you want . It has a 1594323 digit repeating decimal period.
neat number
I have to askQuote: gaspoYes, I meant to include the repeat roll in the count, and yes, the 9/2 ratio certainly suggests that there may be a (relatively) easy mathematical solution. I'm not the guy for that, but am interested to see if someone comes up with something. Thanks!
"Why do you want to know the average number of rolls?"
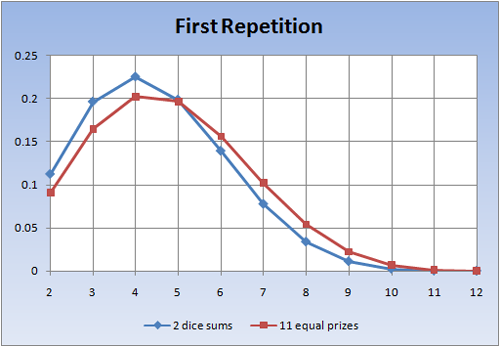
With only 11 sums it should be slightly less than 11 equal sums (prizes) I would think.
That is just 4.8507 and much easier to compute
the distribution
x prob[X=x] prob[X<x] prob[X>=x] prob[X<=x] prob[X>x]
2 0.090909091 0.000000000 1.000000000 0.090909091 0.909090909
3 0.165289256 0.090909091 0.909090909 0.256198347 0.743801653
4 0.202854996 0.256198347 0.743801653 0.459053343 0.540946657
5 0.196707875 0.459053343 0.540946657 0.655761218 0.344238782
6 0.156472173 0.655761218 0.344238782 0.812233392 0.187766608
7 0.102418150 0.812233392 0.187766608 0.914651542 0.085348458
8 0.054312655 0.914651542 0.085348458 0.968964197 0.031035803
9 0.022571493 0.968964197 0.031035803 0.991535690 0.008464310
10 0.006925344 0.991535690 0.008464310 0.998461035 0.001538965
11 0.001399059 0.998461035 0.001538965 0.999860094 0.000139906
close to the shape of what miplet came up with
Rolls Probability
2 0.112654321
3 0.1967592593
4 0.2258659122
5 0.1990883631
6 0.1395897766
7 0.07790057701
8 0.0339742293
9 0.01116541789
10 0.002596243862
11 0.0003796973656
12 0.00002620245309
Sum 1 mean: 4.500070717
Sally


