Surface to air missile problem.
November 10th, 2013 at 3:30:39 PM
permalink
There is an airplane 5,000 meters directly overhead. You shoot a heat-seeking missile it from the ground. The missile is always traveling directly towards the plane. The plane can travel 10,000 meters per minute, travels in a straight line and maintains the same altitude. The missile can travel 11,000 meters per minute. How long will it take the missile to strike the plane?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 10th, 2013 at 3:38:09 PM
permalink
Before you can get back from the bathroom in the rear
of the plane?
What did I win.
of the plane?
What did I win.
"It's not called gambling if the math is on your side."
November 10th, 2013 at 4:13:27 PM
permalink
7 minutes
November 10th, 2013 at 4:24:43 PM
permalink
it's a trick question.
if the plane is a f-22 raptor, then on paper it evaded the missile.
if the plane is the f-35 joint strike fighter, then it never left the ground.
if the missile is American made, then it never hits the plane even if it's a crop duster.
Am I rite?
if the plane is a f-22 raptor, then on paper it evaded the missile.
if the plane is the f-35 joint strike fighter, then it never left the ground.
if the missile is American made, then it never hits the plane even if it's a crop duster.
Am I rite?
Craps is paradise (Pair of dice).
Lets hear it for the SpeedCount Mathletes :)
November 10th, 2013 at 4:36:46 PM
permalink
I'm going to guess that the correct answer involves sine or cosine and an integral. That leaves me out of it.
Someday, joor goin' to see the name of Googie Gomez in lights and joor goin' to say to joorself, "Was that her?" and then joor goin' to answer to joorself, "That was her!" But you know somethin' mister? I was always her yuss nobody knows it! - Googie Gomez
November 10th, 2013 at 5:07:21 PM
permalink
You fire on a plane as it approaches ... and when its climbing so its countermeasures are least effective. If the plane is already overhead, the heat is likely to be going away, not approaching. What plane fails to take evasive action? And its the plane that strikes the missile!!
November 10th, 2013 at 5:31:28 PM
permalink
On second thought, this is a compound interest problem. Sine and Cosine may not be directly involved but I think e is thrown in there somewhere. So let's break it down in the spoiler button:
My answer then is 3 minutes and 36 seconds
The missile must travel at a minimum, 5000 meters so it will take at least .. 11,000 meters per minute = 183.333 meters per second
5000 / 183.333 = 27.27 seconds.
Break it into two chunks of 15 seconds:
1) missile travels straight up 2750 meters
plane travels 2500 meters
Now they are 3700 meters apart
2) missile travels at an angle 2750 meters
plane travels another 2500 meters
missile at altitude of about 4700
distance is now about 3100 apart
3) the angle becomes negligible so the rest is covering the remaining 3100 meters
since the distance closed is 1000 meters per minute, I give it another 3 minutes and 6 seconds
5000 / 183.333 = 27.27 seconds.
Break it into two chunks of 15 seconds:
1) missile travels straight up 2750 meters
plane travels 2500 meters
Now they are 3700 meters apart
2) missile travels at an angle 2750 meters
plane travels another 2500 meters
missile at altitude of about 4700
distance is now about 3100 apart
3) the angle becomes negligible so the rest is covering the remaining 3100 meters
since the distance closed is 1000 meters per minute, I give it another 3 minutes and 6 seconds
My answer then is 3 minutes and 36 seconds
Someday, joor goin' to see the name of Googie Gomez in lights and joor goin' to say to joorself, "Was that her?" and then joor goin' to answer to joorself, "That was her!" But you know somethin' mister? I was always her yuss nobody knows it! - Googie Gomez
November 10th, 2013 at 5:40:40 PM
permalink
No correct answers so far.
The integral of (1+x^2)^0.5 dx = ln(x + (1+x^2)^0.5) + constant of integration.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 10th, 2013 at 6:51:06 PM
permalink
I'm so far away from my days of acing the algebra final. I've forgotten what a logarithm is. I think it has something to do with exponents and even those give me pause nowadays. Could you tell me if my guess was within 10%? I can still handle percentages.Quote: WizardNo correct answers so far.
The integral of (1+x^2)^0.5 dx = ln(x + (1+x^2)^0.5) + constant of integration.
Someday, joor goin' to see the name of Googie Gomez in lights and joor goin' to say to joorself, "Was that her?" and then joor goin' to answer to joorself, "That was her!" But you know somethin' mister? I was always her yuss nobody knows it! - Googie Gomez
November 10th, 2013 at 7:27:39 PM
permalink
Approximately 1 minute and 40 seconds.
November 10th, 2013 at 7:53:00 PM
permalink
Constant of integration..... so which is White and which is Black? And doesn't the integration take place only when the disintegration takes place? And I know nothing about these ponents everyone is talking about either present ponents or ex-ponents.
November 10th, 2013 at 8:01:27 PM
permalink
Sorry, no.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 10th, 2013 at 8:31:25 PM
permalink
In 1989 I interviewed for the coolest job in the world. It was a position for a firmware engineer for Ford Aerospace. The position was for developing firmware for air to air missiles. I was told that every four to five weeks you you get to got out to the test range and test fire the missile with your firmware. Sadly I didn't get the position, that would have been my dream job.
At my age, a "Life In Prison" sentence is not much of a deterrent.
November 10th, 2013 at 11:16:40 PM
permalink
Well, it's a right triangle with a constantly increasing side b and a parabola for a hypotenuse; the arc will be slightly longer but constantly correcting closer to the hypotenuse. I get about 1 minute, 12 seconds, but not sure how to plug in the formula you suggest using for an exact answer.
If the House lost every hand, they wouldn't deal the game.
November 10th, 2013 at 11:30:26 PM
permalink
Approximately 53.4 seconds, give or take a few tenths.
November 10th, 2013 at 11:35:09 PM
permalink
I say 1 minute.
Sanitized for Your Protection
November 11th, 2013 at 12:44:57 AM
permalink
60.54 sec.
November 11th, 2013 at 12:48:25 AM
permalink
Each minute missle gets ahead of the plane by 1 km when traveled in a straight line. Let's simplify the problem: how far ahead of the plane should the missile be fired vertically in order to hit the plane? It takes 30 seconds to reach the plane if plane is stationary. The missile hasto be ahead of the plane by at least 30 seconds. Plane will travel 5 km in 30 seconds, so the missile has to be ahead of plane at least 5 km. it will need 5 minutes to do that. Now we have to find what is the optimum angle at which the missile has to be fired? Let say 45 degrees it gives us 7 km or 7 minutes.
November 11th, 2013 at 3:12:09 AM
permalink
For the military these problems were life and death to solve.
For firing torpedoes, a moving launcher [usually a sub of course] launching an underwater guided missile [what a torpedo basically was] to hit another moving object was a tough one, even if the target was staying same heading, same speed. That in WW2 US submarines had a machine on board to quickly calculate what was called "the solution" was top-secret for many many years after the war.
I will try to remember to do a related non-mathematical trivia question once this one runs its course.
For firing torpedoes, a moving launcher [usually a sub of course] launching an underwater guided missile [what a torpedo basically was] to hit another moving object was a tough one, even if the target was staying same heading, same speed. That in WW2 US submarines had a machine on board to quickly calculate what was called "the solution" was top-secret for many many years after the war.
I will try to remember to do a related non-mathematical trivia question once this one runs its course.
the next time Dame Fortune toys with your heart, your soul and your wallet, raise your glass and praise her thus: “Thanks for nothing, you cold-hearted, evil, damnable, nefarious, low-life, malicious monster from Hell!” She is, after all, stone deaf. ... Arnold Snyder
November 11th, 2013 at 5:31:12 AM
permalink
I still have not seen the correct answer.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 11th, 2013 at 5:39:17 AM
permalink
Quote: WizardThe missile can travel 11,000 meters per minute.
Even though it's less apparent with a small surface to air missile there is a lag to reaching top speed. (larger example shuttle launch or Saturn 5). So I assume that has to be calculated as well.
Sanitized for Your Protection
November 11th, 2013 at 5:44:17 AM
permalink
Quote: rxwineEven though it's less apparent with a small surface to air missile there is a lag to reaching top speed. (larger example shuttle launch or Saturn 5). So I assume that has to be calculated as well.
For the sake of simplicity, assume the missile always travels at 11,000 meters per minute. The problem is hard enough as it is.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 11th, 2013 at 7:23:01 AM
permalink
ds/dt=11000 meters/min
dx/dt=10000 meters/min
dy/dt=4582.5757 meters/min
To travel 5000 meters would take 1.09109 minutes or 65.465 seconds
I am not sure that you really need to do the line integral.
November 11th, 2013 at 7:47:58 AM
permalink
Quote: pacomartinI am not sure that you really need to do the line integral.
I am not sure that you got the right answer.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 11th, 2013 at 7:56:31 AM
permalink
It doesn't make sense, intuitively, to me, but I get:
I first calculated paco's answer as a theoretical minimum amount of time.
154.22 seconds
I first calculated paco's answer as a theoretical minimum amount of time.
I heart Crystal Math.
November 11th, 2013 at 7:59:32 AM
permalink
Quote: Dicenor33Each minute missle gets ahead of the plane by 1 km when traveled in a straight line. Let's simplify the problem: how far ahead of the plane should the missile be fired vertically in order to hit the plane? It takes 30 seconds to reach the plane if plane is stationary. The missile hasto be ahead of the plane by at least 30 seconds. Plane will travel 5 km in 30 seconds, so the missile has to be ahead of plane at least 5 km. it will need 5 minutes to do that. Now we have to find what is the optimum angle at which the missile has to be fired? Let say 45 degrees it gives us 7 km or 7 minutes.
You're talking about a bullet (without ballistic drop), not a missile.
November 11th, 2013 at 8:07:00 AM
permalink
Quote: CrystalMathIt doesn't make sense, intuitively, to me, but I get:
154.22 seconds
That is close to my answer, but not quite. I confirmed my answer with a spreadsheet that tracked the coordinates of the missile, making angle adjustments every 0.001 minutes.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 11th, 2013 at 8:22:05 AM
permalink
Oops:
157.14 seconds
I heart Crystal Math.
November 11th, 2013 at 8:26:21 AM
permalink
OK, second estimate is 2.6 minutes = 156 seconds.
November 11th, 2013 at 9:50:40 AM
permalink
OK, I guess I admit defeat. It's been too long since I have tried such things. Have you folks who feel that you got the correct answer been getting an explicit, analytical solution or some kind of approximation?
I think that pacomartin made
though I may have misinterpreted his answer.
I wind up with too many variables that I cannot substitute to get fewer. Here are
t=time
s=distance along the missile's path
x=horizontal position of the missile, x=0 at t=0
y=vertical position of the missile, y=0 at t=0 and y=5000 at impact
missile speed = 10000
ds/dt=11000
From the given that the missile is always pointed at the target:
dy/dx=(5000-y)/(10000*t-x) or dx/dy=(10000*t-x)/(5000-y)
ds=(1+(dy/dx)^2)^0.5) dx or ds=(1+(dx/dy)^2)^0.5) dy
I have not been able to figure out how to combine those to get y as just a function of t. When I separate variables (in order to integrate), I can get just y on one side but both x and t on the other.
Brain dead, I guess.
I think that pacomartin made
dx/dt=10000 is for the target, not for the missile
though I may have misinterpreted his answer.
I wind up with too many variables that I cannot substitute to get fewer. Here are
t=time
s=distance along the missile's path
x=horizontal position of the missile, x=0 at t=0
y=vertical position of the missile, y=0 at t=0 and y=5000 at impact
missile speed = 10000
ds/dt=11000
From the given that the missile is always pointed at the target:
dy/dx=(5000-y)/(10000*t-x) or dx/dy=(10000*t-x)/(5000-y)
ds=(1+(dy/dx)^2)^0.5) dx or ds=(1+(dx/dy)^2)^0.5) dy
I have not been able to figure out how to combine those to get y as just a function of t. When I separate variables (in order to integrate), I can get just y on one side but both x and t on the other.
Brain dead, I guess.
November 11th, 2013 at 10:45:02 AM
permalink
Quote: CrystalMathOops:
157.14 seconds
Bingo! For extra credit:
1. Give an exact form of the answer.
2. Given an equation for the coordinates of the missile.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 11th, 2013 at 10:54:52 AM
permalink
Quote: Dicenor33Each minute missle gets ahead of the plane by 1 km when traveled in a straight line. Let's simplify the problem: how far ahead of the plane should the missile be fired vertically in order to hit the plane? It takes 30 seconds to reach the plane if plane is stationary. The missile hasto be ahead of the plane by at least 30 seconds. Plane will travel 5 km in 30 seconds, so the missile has to be ahead of plane at least 5 km. it will need 5 minutes to do that. Now we have to find what is the optimum angle at which the missile has to be fired? Let say 45 degrees it gives us 7 km or 7 minutes.
One condition of the problem is that the missile is ALWAYS pointed at the plane. Assuming the missile is launched the exact moment the plane passes overhead, the missile is aimed straight up for a split second, then begins to tilt by fractions of degrees to near (but not quite) horizontal by the moment of impact, because any vector on the true horizontal is wasted optimum tracking.
So you don't get to lead the shot like a duck hunter; the missile has to track along an arc above the hypotenuse (the hypothetical shortest distance to impact), and the length of the arc travelled in seconds is the answer. It would be just slightly more than 1 minute via the hypotenuse route if you could lead it; it's longer because of the constant corrections made while gaining altitude. How much longer, I think, is the question.
If the House lost every hand, they wouldn't deal the game.
November 11th, 2013 at 10:59:49 AM
permalink
Gee Babs, your post is making me think your membership in the Whirly-Girls is not just an honorary one.
Shed not for her
the bitter tear
Nor give the heart
to vain regret
Tis but the casket
that lies here,
The gem that filled it
Sparkles yet
November 11th, 2013 at 11:03:16 AM
permalink
Quote: WizardQuote: CrystalMathOops:
157.14 seconds
Bingo! For extra credit:
1. Give an exact form of the answer.
2. Given an equation for the coordinates of the missile.
I was hoping you would provide that. I must confess that my answer is a numerical solution in which the angle was recalculated 1 million times per second. My issue with my first answer was the following declaration:
double missile_speed = 11000/60;
Stupid Java! I changed it to 11000.0/60.0 before arriving at the correct(ish) solution.
My hope was that doing a numerical solution would guide me to being able to do a closed form solution, but then I remembered that I have work to get done :)
I heart Crystal Math.
November 11th, 2013 at 11:06:52 AM
permalink
I know that I did something very close to this in college. Heck I know I solved it. It's calculus.
Because the missile travels in an arc facing the target at each point and not in a straight line, you have to calculate the point of impact on a curved surface. It's fine to calculate the x and y coordinates of both the missile and the target but I can't quantify how to calculate the path of the missile over time. You can calculate the position of the satellite as a sin and cos function knowing the angular velocity of the satellite. Then perhaps you could make the satellite a stationary body and solve the problem of an approaching object and make the angular space normal space. To the point of view of the satellite, it is stationary while the missile moves in curved space.
I wasted about 90 minutes of worktime trying to figure this out this morning, and if I wasn't going live in 3 days with my work project, I'd spend the whole frickin' day on it.
Interesting.
Because the missile travels in an arc facing the target at each point and not in a straight line, you have to calculate the point of impact on a curved surface. It's fine to calculate the x and y coordinates of both the missile and the target but I can't quantify how to calculate the path of the missile over time. You can calculate the position of the satellite as a sin and cos function knowing the angular velocity of the satellite. Then perhaps you could make the satellite a stationary body and solve the problem of an approaching object and make the angular space normal space. To the point of view of the satellite, it is stationary while the missile moves in curved space.
I wasted about 90 minutes of worktime trying to figure this out this morning, and if I wasn't going live in 3 days with my work project, I'd spend the whole frickin' day on it.
Interesting.
-----
You want the truth! You can't handle the truth!
November 11th, 2013 at 11:16:45 AM
permalink
I was off by only a minute!
Someday, joor goin' to see the name of Googie Gomez in lights and joor goin' to say to joorself, "Was that her?" and then joor goin' to answer to joorself, "That was her!" But you know somethin' mister? I was always her yuss nobody knows it! - Googie Gomez
November 11th, 2013 at 11:17:01 AM
permalink
Quote: WizardFor extra credit:
1. Give an exact form of the answer.
2. Given an equation for the coordinates of the missile.
I guess I was working (unsuccessfully) on the extra credit problem rather than trying to find the (practical) answer by approximation/iteration/numerical methods. Of course, I was taking college calculus back while Kennedy was president -- the brain does atrophy from years of disuse.
November 11th, 2013 at 11:23:07 AM
permalink
Counterintuitive is right. How can it take more than 2 1/2 minutes with a constant overtake to overcome only 5000 feet of altitude? The shortest route is only 11180.399 meters from point of missile launch to where the airplane is after 1 minute of flight, and at that point the missile has flown 11000 meters, correcting all the way. It has to have overcome more than 1/2 of the altitude needed in that first minute. And made significant horizontal progress, though apparently not as much as I expected. The curve must look like nearly an inner border to the altitude-flight path angle to be that far behind it.
I hope I can "see" it in the math, because it sure seems like that's way longer than I would have thought.
I hope I can "see" it in the math, because it sure seems like that's way longer than I would have thought.
If the House lost every hand, they wouldn't deal the game.
November 11th, 2013 at 11:31:31 AM
permalink
When someone figures it out, please post the equation for the flight path of the missile where x=distance downrange y=altitude. I want to plug it into WolframAlpha.
Someday, joor goin' to see the name of Googie Gomez in lights and joor goin' to say to joorself, "Was that her?" and then joor goin' to answer to joorself, "That was her!" But you know somethin' mister? I was always her yuss nobody knows it! - Googie Gomez
November 11th, 2013 at 11:53:30 AM
permalink
Quote: s2dbakerWhen someone figures it out, please post the equation for the flight path of the missile where x=distance downrange y=altitude. I want to plug it into WolframAlpha.
Let
x=horizontal distance from point of firing.
y=vertical distance from earth.
x = (55/2)*[((5-y)/5)^(21/11) - ((5-y)/5)^(1/11)] + (55/21)
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 11th, 2013 at 12:35:54 PM
permalink
Quote: CrystalMathIt doesn't make sense, intuitively, to me, but I get:
154.22 seconds
I don't know where they actually point heat seeking missiles (if this is one), but seems like they would still try to lead the target if possible. If the target is directly overhead I would think it would still be smart to point out ahead of where the plane seems to be going. The tip of the missile in this case is pointing where the plane is definitely not going to be and has to constantly turn to follow. Seems like wasted motion, if you actually fired one that way on purpose.
Sanitized for Your Protection
November 11th, 2013 at 1:02:35 PM
permalink
A heat seeker will always chase. The hot stuff is at the ass end of the engine/aircraft. The flight path of a radar guided missile can be different.
November 11th, 2013 at 1:03:48 PM
permalink
Quote: rxwineQuote: CrystalMathIt doesn't make sense, intuitively, to me, but I get:
154.22 seconds
I don't know where they actually point heat seeking missiles (if this is one), but seems like they would still try to lead the target if possible. If the target is directly overhead I would think it would still be smart to point out ahead of where the plane seems to be going. The tip of the missile in this case is pointing where the plane is definitely not going to be and has to constantly turn to follow. Seems like wasted motion, if you actually fired one that way on purpose.
I agree. It is far better to track the target for a few moments and estimate where it is going. If you lead the target, you can hit it as fast as paco's answer.
I heart Crystal Math.
November 11th, 2013 at 3:22:12 PM
permalink
Here is an image of the flight path.
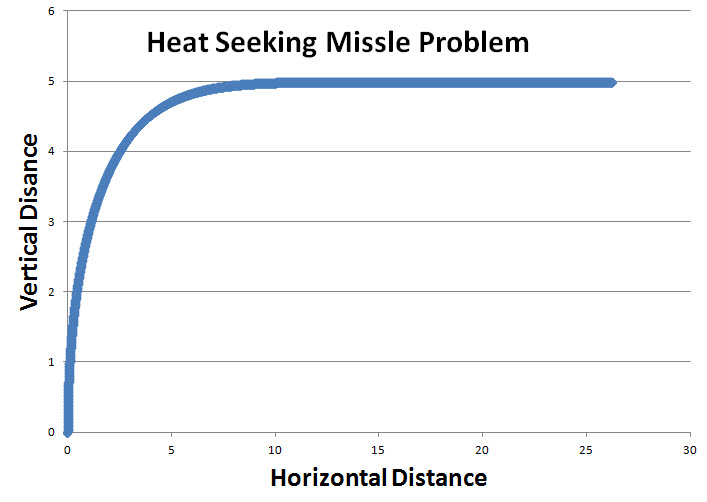
All distances and speeds have been divided by 1,000.
As stated in the problem, the shooter fires directly straight up at the plane. Notice how it takes a pretty sharp turn and then plays catch up with the plane.
Note that the curve ends at 26.2 units, which is where it will hit the plane. Recall the plane travels at 10 units per minute, so it will take 2.62 units of time to reach the plane.
By the way, if anyone knows how to make an animated gif, I'd be happy to provide the coordinates of both the plane and missile, to aid in making one.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 11th, 2013 at 3:25:04 PM
permalink
Quote: Wizard
Here is an image of the flight path.
All distances and speeds have been divided by 1,000.
As stated in the problem, the shooter fires directly straight up at the plane. Notice how it takes a pretty sharp turn and then plays catch up with the plane.
Note that the curve ends at 26.2 units, which is where it will hit the plane. Recall the plane travels at 10 units per minute, so it will take 2.62 units of time to reach the plane.
I am proud of myself. I got that this would be the image of the flight path pretty quickly and recognized the image as a graph from high school math, unfortunately that is as much as I am capable of :(
Vote for Nobody 2020!
November 11th, 2013 at 3:30:43 PM
permalink
Quote: DocI guess I was working (unsuccessfully) on the extra credit problem rather than trying to find the (practical) answer by approximation/iteration/numerical methods. Of course, I was taking college calculus back while Kennedy was president -- the brain does atrophy from years of disuse.
Doc did you ever have a math class with Ben Klein in college? He taught me 10ish years ago as a senior prof and he was a young prof in the early 70's so I thought we might have this overlap. BTW Duke beat the hell out of our beloved 'Cats last week. How often does a 16 point favorite win by (gulp) 44 points in the NCAA? woulda been a good one to do a pleaser card on.
Vote for Nobody 2020!
November 11th, 2013 at 6:07:42 PM
permalink
Quote: WizardI am not sure that you got the right answer.
Sorry
I did calculate the most efficient way to close on the target, but I forgot that you said that the missile must always be pointing at the target. I did calculate the theoretical minimum time to intercept. My number assumes you the missile is always pointing ahead of the target (which is realistic).
You do have to do the line integral and have dx/dt go from zero to 11,000 and dy/dt go from 11,000 to zero and dy/dx go from infinity to zero.
November 11th, 2013 at 6:19:41 PM
permalink
Quote: CrystalMathI agree. It is far better to track the target for a few moments and estimate where it is going. If you lead the target, you can hit it as fast as paco's answer.
Since an actual target is trying to do evasive manueauvers you do point ahead of them for a while, but eventually you try to get into a tail chase. As a countermeasure the pilot blows chaff to try and confuse the missile.
If you are chasing a submarine with a torpedo you traditionally hit the screws and disabled the submarine forcing it to surface. Then you had the leisure of taking pot shots until it sank.
Of course that all changed with guided missile or ballistic missile submarines. Just hitting the screws meant that the crew was very motivated to kill as many people as possible before they died. They would fire their whole inventory of missiles once they were incapacitated. If cruise missiles they could take out nearby ships, if they had nuclear missiles they could take out cities.
The nuclear missile scenario was particularly frightening because it is feared that the crew might act on their own rather than waiting for orders. Since nuclear warfare strategy was always dependent on a certain reluctance of the highest level of command to start a nuclear war, the wishes of men who expected to die might change the outcome.
A torpedo strategy that would completely incapacitate a submarine on first strike meant that you had to hit something much more important than the screws. As such you need a much faster torpedo.
November 11th, 2013 at 7:15:06 PM
permalink
Quote: bigfoot66Doc did you ever have a math class with Ben Klein in college? ... BTW Duke beat the hell out of our beloved 'Cats last week.
Nope -- Prof. Klein was after my time.
Also, my wife and I just attended the second loss of the season tonight, though it was a much more even game. Another tough challenge coming up this Saturday, too.
November 11th, 2013 at 7:23:53 PM
permalink
You broke WolframAlpha. Congratulations.Quote: Wizard
Let
x=horizontal distance from point of firing.
y=vertical distance from earth.
x = (55/2)*[((5-y)/5)^(21/11) - ((5-y)/5)^(1/11)] + (55/21)
Someday, joor goin' to see the name of Googie Gomez in lights and joor goin' to say to joorself, "Was that her?" and then joor goin' to answer to joorself, "That was her!" But you know somethin' mister? I was always her yuss nobody knows it! - Googie Gomez
