Poll
 | 21 votes (58.33%) | ||
 | 4 votes (11.11%) | ||
 | 1 vote (2.77%) | ||
| No votes (0%) | |||
| No votes (0%) | |||
 | 1 vote (2.77%) | ||
 | 1 vote (2.77%) | ||
| No votes (0%) | |||
| No votes (0%) | |||
 | 8 votes (22.22%) |
36 members have voted
In CS courses the big problem is plagiarism. I told students that they could discuss ideas together, but that they could not write code for each other, figure out code together, debug eachother's code or copy code. It often happened that students emailed their code to a friend with the idea that the other student would look at it to get an idea for how to do it. The second student would then just copy it and turn in their friend's code with the variable names changed and a bit of reformatting on the page. When the courses were Linux based, students learned how to go into eachother's home directory and copy files back to their own accounts. We learned the chmod command very early. But there were some students who scavanged for unprotected code.Quote: rdw4potus(cheating) Does it really happen that often, and what did you DO to the people you caught?!?
It is trivial to catch such plagiarism, even in a course with 200 students, using automated scripts.
My penalty for a first offense was that the student fail the course and be sent to the academic judiciary for plagiarism. That usually resulted in a one or two quarter suspension. It was bad. That's why everyone warned each other not to cheat. I had a zero-tolerance policy.
Professors who merely fail students who cheat are incentivizing cheating. If a student is failing, what does he risk by cheating? It is a plus EV move to cheat. That's crazy. Yet, most professors feel as though it is too tough to even fail cheating students, giving them a waring first. I had none of that.
Don't ask me to defend it now, it was just what I did to deal with the rampant cheating that was going on in the CS department at UCSB.
Two students turned in the same (badly formatted) resume with only the name changed at the top. I would probably have not noticed if they hadn't handed it in -next to each other in the returns box-.
Considering they final year students, about to graduate and needed this course to complete their credits... they were lucky I was told not to fail them under plagarism, but make them resit under closed conditions.
The fact a final year student couldn't work out that creating a decent resume NOW for course credit would also be useful when applying for jobs was grounds to me for them to fail their degrees for not having learnt sod all in three years.
At the beginning of each term, I made it very clear in both the syllabus and in lecture #1 that I did not tolerate such conduct. I said that in any case where I believed a student was cheating, I would report the incident to the Dean of Students. If it was determined that the student indeed had been cheating, I would assign a grade of F for unsatisfactory performance in my class, in addition to whatever disciplinary action that the dean (or the student honor committee) imposed.
Under the procedures at that school, the dean would summon the accused student and read the accusation(s) made against him/her. The student had the option of admitting or denying guilt. If the student denied guilt, the case was automatically referred to the student honor committee. If the student admitted guilt, he/she was given the options of either (1) having the student honor committee review the incident and determine the measures to be taken or (2) allowing the dean to determine the measures administratively. A bit unfortunately, the dean at that time was very soft (in my opinion) on most cases of cheating; this apparently was well known among the students who chose to cheat, so they almost always admitted guilt and accepted his minimal punishment. Sometimes it seemed to be little more than sending them a letter (and filing a copy) that said essentially, "Don't get caught cheating any more."
After encountering that on several occasions, I changed my approach. When reporting incidents to the dean, I no longer gave any details of any proof that I had. I just described what I believed had occurred. Because of that new approach, several students, when they were read the accusation, believed it would just be their word against mine, so they denied any guilt. That led to us meeting before the student honor committee, where I was able to put on display substantial proof of their guilt. Both the student and the members of the honor committee were generally in shock when I finished the presentation.
I know at least one student who never received her degree as a result of misconduct in my class and my insistence that the rules be enforced.
Solution to e^(pi*i) (pdf). I hope creating this document will serve as my punishment for bothering Eliot.
Quote: WizardSorry to get back on topic. Please check out my solution to the problem at hand, based on Taylor's Formula.
Solution to e^(pi*i) (pdf). I hope creating this document will serve as my punishment for bothering Eliot.
Nice! Also, I kind of want to block out the bit at the bottom of page three and submit that as my own work:-)
Quote: WizardSorry to get back on topic. Please check out my solution to the problem at hand, based on Taylor's Formula.
Solution to e^(pi*i) (pdf). I hope creating this document will serve as my punishment for bothering Eliot.
I think the proof is incomplete. When handling with series, you first need to prove that they converge....
... otherwise
0 = 1 - 1 + 1 - 1 + 1 ... = 1 + (-1 + 1 - 1 + 1 - 1 + ...) = 1
Quote: MangoJI think the proof is incomplete. When handling with series, you first need to prove that they converge....
Uh oh. I'm not sure my proof is going to get much better than that with my rusty calculus skills.
Quote: WizardI've been meaning to post a solution to epi*i using Taylor, but between a lack of time and that I don't know how to make mathematical symbols in any kind of electronic document, I haven't. Yet. I plan to just write out a solution by hand and scan it.
Latex is relatively easy to learn and you can do just about everything in it. Integrals and summations are a breeze. Just get a template to start with and you'll have professional math proofs in a few hours. (http://en.wikipedia.org/wiki/LaTeX , http://latex-project.org/).
edit:*It would only take a few hours the first time to become accustomed to the markup language. Then it would take only slightly longer than writing something in Word, which is much shorter than trying to insert a bunch of math stuff in a normal document program.
I see you typed it well in Word, so nevermind... :)
Quote: MangoJI think the proof is incomplete. When handling with series, you first need to prove that they converge....
... otherwise
0 = 1 - 1 + 1 - 1 + 1 ... = 1 + (-1 + 1 - 1 + 1 - 1 + ...) = 1
As I posted back on page 1, Wiki points out -- and gives an example that shows -- that it's even possible for the Taylor Series to converge but be equal to something different from the original function. Either I had never heard that or completely forgot. Plus, I still don't really understand that. Note: I was never a math major.
cos(x) + i*sin(x) = c*e^(i*x) for some constant c.
Plug in x = 0 to get c = 1.
Done.
Quote: DocQuote: MangoJI think the proof is incomplete. When handling with series, you first need to prove that they converge....
... otherwise
0 = 1 - 1 + 1 - 1 + 1 ... = 1 + (-1 + 1 - 1 + 1 - 1 + ...) = 1
As I posted back on page 1, Wiki points out -- and gives an example that shows -- that it's even possible for the Taylor Series to converge but be equal to something different from the original function. Either I had never heard that or completely forgot. Plus, I still don't really understand that. Note: I was never a math major.
Again, as long as it's infinitely differentiable at every point from where you are to the origin (for a Maclaurin series), you're good to go.
What's more, it can be easily seen by the ratio test (i.e., if the ratio between successive terms approaches anything of absolute value strictly less than 1, the series converges) that all those series converge.
Quote: 24BingoAgain, as long as it's infinitely differentiable at every point from where you are to the origin (for a Maclaurin series), you're good to go.
So here's the example that Wiki uses and which I cannot explain/understand.
Given the function:
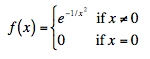
This is infinitely differentiable at x = 0, and has all derivatives zero there. Consequently, the Taylor series of f(x) about x = 0 (Maclaurin series) is identically zero. However, f(x) is not equal to the zero function, and so it is not equal to its Taylor series around the origin.
If this infinitely-differentiable function is not represented by its convergent Taylor series, how do we know that other functions are? (Obviously, my math is a bit weak these days.)
Although nothing looks special on the real axis, x = 0 is actually a singularity in the complex domain.
Quote: DocThanks, MangoJ, though I'm still a bit in that don't-really-understand state. Do folks using Taylor series expansions and approximations "normally" investigate a function through a full complex domain when the function does not explicitly contain i or any fractional radicals of numbers that might be negative?
Good question. I'm eager to see the answer.
Quote: DocDo folks using Taylor series expansions and approximations "normally" investigate a function through a full complex domain when the function does not explicitly contain i or any fractional radicals of numbers that might be negative?
Sometimes one has to step up and view the problem in a higher dimensional space to oversee it. The representation of functions by it's Taylor series, among all properties like convergence, is a byproduct of the field named "complex analysis" which is the study of holomorphic functions (i.e. functions that are differentiable in the complex domain).
I'm not a mathematician, so I don't know all the details. But if a function f(x) (for real x) has a holomorphic counterpart g(z) (for complex z) with f(x) = g(x) for some interval on the real axis, then the power series expansion for f(x) and g(z) on that interval are the same - this might sound trivial (and probably is).
Now the essence of holomorphic functions is: this very power series also describes g(z) in the complex domain, i.e. away from the real axis. In the complex domain the convergence set is always a circle, and always reaches in z until it "hits" a divergence poles of g(z) (hence called convergence "radius").
Since the convergence set also includes the real axis, and it is the same power series, the convergence radius of a real functions Taylor series is purely determined by the divergence poles of if's holomorphic continuation g(z).
A simple example: The function f(x) = 1 / (1 + x^2) has a power series expansion of 1 - x^2 + x^4 - ... From the power series one immediately see that x>1 diverges. But f(1) is nothing special. The complex continuation of f(x) is g(z) = 1 / (1 + z^2) with the same power series 1 - z^2 + z^4 - ...
For g(z), it diverges at z=i and -i. So the convergence radius of both series is 1.
Hope that will help somehow.
Quote: DocSo here's the example that Wiki uses and which I cannot explain/understand.
Given the function:
exp(Z) = 1 +Z+ Z^2/2!+... Z^k/k! ...
exp(-1/x^2) = 1 -1/x^2+ 1/x^4/2!+... (-1)^k/k!/x^(2k) ...
which clearly is not convergent.
It would help if you graphed
Y=exp(-1/x^2) for positive and negative x for different value of x from -1 to +1 (but not x=0) but use a logarithmic scale for y
While the function is continuous, as x approaches zero from the positive side, the first derivative goes to positive infinity, but as x approaches zero from the negative side, the first derivative goes to negative infinity
Quote: pacomartinexp(Z) = 1 +Z+ Z^2/2!+... Z^k/k! ...
exp(-1/x^2) = 1 -1/x^2+ 1/x^4/2!+... (-1)^k/k!/x^(2k) ...
which clearly is not convergent.
How about exp(-1/x) ? By your same argument, is exp(-1/x) = 1 -1/x +... (-1)^k/k!/x^k ... also not convergent ? (Because it is).
Quote: pacomartinWhile the function is continuous, as x approaches zero from the positive side, the first derivative goes to positive infinity, but as x approaches zero from the negative side, the first derivative goes to negative infinity
Are you sure about that? My calc is a bit rusty, but I think the first derivative approaches zero as x approaches 0, coming from either side. I think all of the derivatives (in the real number plane, anyway) are zero at the origin.
Quote: DocAre you sure about that? My calc is a bit rusty, but I think the first derivative approaches zero as x approaches 0, coming from either side. I think all of the derivatives (in the real number plane, anyway) are zero at the origin.
y=exp(-1/x^2)
y'=2*exp(-1/x^2)/x^3=2y/x^3
Perhaps you are right. I should have worked it out, as it looks like an indefinite case 0/0 . I have to think about it because if you try L'Hopital's rule it doesn't simplify
lim (x->0) of 2y/x^3 =lim (x->0) of 2/3y'/x^2 = 4/3y/x^5
But I've been wrong quite a few times before.
Quote: DocI think the exponential term dominates the x^3 term in the limit.
That doesn't always help with an indeterminate limit. You can set up two different examples with exponential vs polynomial with indeterminate limits , and they both go to different values.
Example (1) y =(exp(-x)-1)/x
Find lim y as x->0, you quickly get y->0/0
lim y->0 = lim -exp(-x)/1 as x->0 so y-> -1
Example (2) z =(exp(-x)-1)/x^2
Find lim z as x->0, you quickly get z->0/0
lim z->0 = lim -exp(-x)/2x as x->0 so z->-INF
But the original question was does the Taylor series converge? The answer is no, I just screwed up the explanation.
Quote: WizardSorry to get back on topic. Please check out my solution to the problem at hand, based on Taylor's Formula.
Solution to e^(pi*i) (pdf). I hope creating this document will serve as my punishment for bothering Eliot.
The Taylor expansion would permit you to quickly derive the more general expression exp(ix)=cos(x)+i*sin(x) , not just the simpler identity.
Euler actually did the same thing as you in 1748. But the special case of the identity exp(i*pi)+1=0 was probably known before the life of Euler. I am not sure how it was derived without resorting to differential equations or Taylor expansions.
Since, for the function I borrowed from Wiki, I don't seem to be able to solve/prove the values of the derivatives (which approach 0/0 as x --> 0), I tried a hack method to see whether the tendency I expected was supported by a few calculations.
Quote: pacomartiny=exp(-1/x^2)
y'=2*exp(-1/x^2)/x^3=2y/x^3
I used these expressions for y and y', and (hoping that I didn't screw up again) I used y"= 4y/x^6 - 6y/x^4. I put those functions in an Excel spreadsheet and looked at values of x near zero.
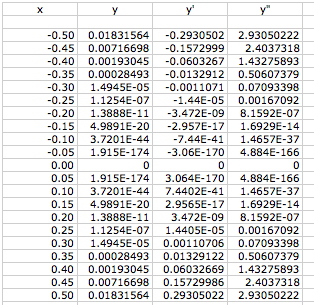
Even if you don't accept the Excel calculation at exactly x=0, it at least looks as if y, y', and y" approach zero as x approaches zero, both in the positive and negative regions. Without calculating them, I repeat my suspicion that all of the (real number domain) derivatives of y approach and are equal to zero at the origin.
Quote: pacomartinBut the original question was does the Taylor series converge? The answer is no, I just screwed up the explanation.
If all of the derivatives of y=f(x) really are zero at the origin, then each term of the Taylor series expansion for y about the origin is identically zero. How can the sum of an infinite number of terms that are identically zero not be convergent? Doesn't it have to "converge" to zero? How would there ever be a non-zero term?
That is what makes it appear that the Taylor expansion for y is the zero function, while y is something quite different. And that is still something I don't understand.
(Yes, it's been a long, long time -- decades -- since I took a math class or read a math text.)
Quote: pacomartin
Quote: Doc
I think the exponential term dominates the x^3 term in the limit.
That doesn't always help with an indeterminate limit. You can set up two different examples with exponential vs polynomial with indeterminate limits , and they both go to different values.
Example (1) y =(exp(-x)-1)/x
Example (2) z =(exp(-x)-1)/x^2
Docs statement is about exp(x) for x->inf, not for x-> 0. And yes it's correct, the exponential functions grows faster than any polynom of x for x->inf.
Your examples at x->0 you can use l'Hospital rule, or (which is equivalent, but more easy to see), approximate exp(-x) as 1 - x, and find that
(1): (exp(-1) - 1) / x = -x / x --> 1
(2): (exp(-x) - 1) / x^2 = -x / x^2 --> -inf.
Quote: Doc
If all of the derivatives of y=f(x) really are zero at the origin, then each term of the Taylor series expansion for y about the origin is identically zero. How can the sum of an infinite number of terms that are identically zero not be convergent? Doesn't it have to "converge" to zero? How would there ever be a non-zero term?
That's the whole point. The Taylor series *does* converge, namely against zero. But it does not converge to the function exp(-1/x^2) as you would naively expect for a Taylor series.
The conclusion is: The Taylor series may or may not be a good representation of the original function. It depends on certain properties of the original function - even a infinite differential function (which is as good as a real function can get) will not guarantee you a good Taylor series.
The miracle is: this paradox is solved by complex analysis, although the original function has no relation whatsoever to complex numbers.
Quote: pacomartinI am not sure how it was derived without resorting to differential equations or Taylor expansions.
If I remember correctly, you can use simple derivation.
Consider e^(ix) and differentiate. You get ie^(ix) for the first order, differentiate again and you have i²e^(ix) = - e^(ix) for the second order. So essentially, e^(ix) is a function f(x) whose second derivative is - f(x).
Now that is true also of cos x and of sin x. Hence, e^(ix) is A cos x + B sin x.
Using some values of x readily produces A=1 and B=i.
Or you can work on the first derivative, simply.
(Yes, I know, you could call that 'differential equation', but I think this reasoning is accessible to any schoolboy without a training in diff eqs.)
I knew that if an open disc around a on the complex plane were everywhere differentiable, then every point on that disc would be equal to the Taylor series at a, but I was worried that might rely on Euler's formula, so I tried to hunt down something analogous from real analysis (in which I've never had formal instruction), and what I found I oversimplified.
This is why... well, long story, but this is why.
Quote: Doc
If all of the derivatives of y=f(x) really are zero at the origin, then each term of the Taylor series expansion for y about the origin is identically zero. How can the sum of an infinite number of terms that are identically zero not be convergent? Doesn't it have to "converge" to zero? How would there ever be a non-zero term?
That is what makes it appear that the Taylor expansion for y is the zero function, while y is something quite different. And that is still something I don't understand.
(Yes, it's been a long, long time -- decades -- since I took a math class or read a math text.)
Well, I made a mistake as well. But it's been a long time since I taught calc and differential equations myself. These are some non-standard problems.
The Gaussian function is also listed in the Wikipedia definition of a flat function uses the same function as an example.
The original statement that you quoted:
And even if the Taylor series of a function f does converge, its limit need not in general be equal to the value of the function f(x). For example, the Gaussian function is infinitely differentiable at x = 0, and has all derivatives zero there. Consequently, the Taylor series of f(x) about x = 0 is identically zero. However, f(x) is not equal to the zero function, and so it is not equal to its Taylor series around the origin.
I agree with you that sentence is confusing.
Quote: kubikulannIf I remember correctly, you can use simple derivation.
Consider e^(ix) and differentiate. You get ie^(ix) for the first order, differentiate again and you have i²e^(ix) = - e^(ix) for the second order. So essentially, e^(ix) is a function f(x) whose second derivative is - f(x).
Now that is true also of cos x and of sin x. Hence, e^(ix) is A cos x + B sin x.
Using some values of x readily produces A=1 and B=i.
Or you can work on the first derivative, simply.
(Yes, I know, you could call that 'differential equation', but I think this reasoning is accessible to any schoolboy without a training in diff eqs.)
The modern development of calculus is credited to Isaac Newton (1643–1727) and Gottfried Leibniz (1646–1716), who provided independent and unified approaches to differentiation and derivative.Jacob Bernoulli (1655 – 1705) first calculated the constant e although Napier had used the value in his logarithm tables without specifically defining the number. Brook Taylor (1685-1731) introduced the Taylor series in 1715. Leonhard Euler lived 1707 to 1783. So Calculus did exist before Euler was born.
Colin Maclaurin (1698 – 1746) got lucky in that the special case of a Taylor series was named after him. Basically he popularized their use in a textbook.
It is known that Euler developed the function exp(ix)=cos(x)+i*sin(x) by looking at Taylor Series expansions.
I believe that the observation that e^(ix) is a function f(x) whose second derivative is - f(x) and so are sine and cosine is not sufficient as there could be other functions with this property. But the Taylor series expansion is sufficient.
The special case of exp(i*PI)+1=0 is said to have been known before Euler.
I am not sure how to evaluate the special case without doing the general case first. Incidentally, I have seen this same question posted on physics forums.

Quote: teliot
I've got to stop reading threads about mathematics here. They are just nonsense. It's a lot easier to "think" things than to take the time to *learn* things.
I understand your frustration, but I assure you that your participation is most welcome. It may help the educated person to tolerate this environment by considering that this is a gambling forum rather than a mathematics forum. It just happens that many gambling questions may be answered using mathematics. Some of the gamblers try to solve their own problems. Many stumble and many re-invent the wheel.
I have seen some cases of "Three Stooges" mathematics here. Someone posts a question, three stooge mathematicians post three different answers, and the poster says "Thanks, guys, that's just what I needed." If you try to set things straight the three stooges pile up on you. Kubikulann has a background similar to yours and I think he is doing quite well and enjoying it.
Imaginary numbers can be approached from the standpoint of the Theory of Equations. At first, only positive solutions to equations were considered valid and negative solutions were ignored. In time, they came to be accepted and interpretations were given to them. Next they encountered square roots of negative numbers in solutions of equations of degree two and higher. They were considered just as useless as solutions as negative numbers had been considered earlier and it was some time before practical uses of them were found. Rene Descartes is credited with the adjective "imiginaire," and it was meant to be derisive. Rather than use the term "imaginary" we more often use the term "complex" to denote numbers that combine a real number with an imaginary one, such as a + bi, were i has the property i2 = -1.
Electrical engineer Charles P. Steinmetz, who had an advanced mathematics training, proposed using complex numbers to represent alternating currents. In that way alternating voltages of different phases could be added algebraically rather than graphically, as had been done before. Ohm's law could be generalized to include inductive and capacitive circuit elements using complex impedances.
Dynamic systems ranging in complexity from an automobile suspension to a B-2 bomber controlled by its automatic pilot may be modeled by a linear differential equation with constant coefficients. These are solved by solving a corresponding algebraic equation, which may be of high degree. Complex solutions to this equation correspond to oscillatory solutions of the differential equation, involving sines and cosines. These indicates oscillatory responses of the automobile or bomber if it is subjected to an impulse disturbance.
The complex plane is sometimes used in analyzing problems in two-dimensional fluid flow. It is not adaptable to three dimensions, however.
The Wizard asks if imaginary numbers are real and if they are useful. Well, all numbers are abstract concepts and as such all are imaginary. Complex numbers just are latecomers in terms of being appreciated and in uses being found for them.
Here is how "i" is defined algebraically, from the so-called "Theory of Equations."Quote: puzzlenutImaginary numbers can be approached from the standpoint of the Theory of Equations.
First, x2 + 1 is irreducible over R (real numbers), so <x2 + 1 > is a prime ideal, hence maximal, in the polynomial ring R[x] and R[x]/<x2 + 1> is a field. Define C (complex numbers) to be the splitting field for x2 + 1 over R, which is isomorphic to R[x]/<x2 + 1>; "i" is then defined to be the coset x + <x2 + 1>. Done. This is first-year "abstract algebra" for a college math major, typically a junior level course.
Apparently the traditional "Theory of Equations" is no longer an academic subject. I once gave a talk to some of the professors at Hunter College on the subject of numerical methods of finding roots. One of them asked "What about the case of multiple roots?" I answered "That's simple. You just find the greatest common divisor of the equation and its derivative," and he asked "How do you do that?"
That particular professor teaches a course in abstract algebra and can easily demonstrate that it is impossible to solve an equation of degree five or higher by means of a formula. Who cares! You can't find the roots of a cubic algebraically either when all roots are real. I once got into a debate about this with Prof. David Rusin of the University of Northern Illinois and he tried to tell me that an expression involving the unresolved cube roots of a complex number was perfectly acceptable as a solution. Imagine a college professor being stymied at finding the roots of a cubic when the roots are 2, 3, and 4!
One may find a traditional approach to the theory of equations in the books by Uspensky and Burnside. The latter is available on line. Practical methods of finding numerical solutions are given in books on numerical analysis.
Really? I don't think a junior level undergraduate course is obfuscating. Arrogant or not, this is not Ph.D. level stuff, it's basic undergraduate algebra. I taught this to plenty of people who didn't ever consider a career as a professor of mathematics -- they either were required or wanted to take the course, whether they sought a high-school teaching credential, a would-be actuary, an aspiring meteorologist, a pure math major for its own sake (like any liberal arts major) or whatever. Some physics majors and philosophy majors take these types of "theory" courses as well. And true, some who take it go on to graduate school in mathematics.Quote: puzzlenutTeliot: I should have said "From the history of the theory of equations." I am trying to simplify the concept for the sake of the gamblers. I think that with this terminology you are obfuscating it.
When you say that i is the thing with the property i2 = -1, the question of "why does i exist?" remains. My reply above completely answered this question.
Quote: puzzlenutIf it's any consolation, I too have been described as "arrogant," and it an impression I am trying to correct. I think that confidence in one's position may be mistaken for arrogance.
Confidence - Surety - in one's position is a reason for steadfastness, not for protest or any other posture that exudes an arrogance.
People are not considered arrogant by accident, or because of having strong confidence in some position.
There is a difference between simply being right, and pushing a point too far. One can be both "correct on an issue" and "humble about it."
Marriage is a great teacher on this balance. Being correct and knowledgeable about some fact or situation, and coming off as an arrogant person about it, are two entirely different things. Junior level college work may indeed be obfuscating to many of those interested in gambling, as well as very fine for a math conceptual thread.
And of course, keeping promises is important as well, right?Quote: PaigowdanOne can be both "correct on an issue" and "humble about it."
Quote: teliotAnd of course, keeping promises is important as well, right?
Promises were kept. Accept it and be humble.
Okay, I'll check my mailbox again. Sorry for the O.T.Quote: PaigowdanPromises were kept. Accept it and be humble.
Now, I would like to drop this.
My comments on 'being correct about something' versus 'being arrogant about something' was a discussion point brought on by puzzlenut, and I was making a general comment on this distinction, this difference as it occurs in debate; I wasn't referring to you or even mentioned you or any old history here.
I was saying here is that "being fully right and fully humble" on something (such as a mathematical argument, or a marital argument) has a tricky knack to it for many to carry out smoothly, - on being both right about something, and being discreet and peaceable. I've seen many conceptual math threads and debates descend into some ad hominem attacks, and I think one can be "right" without being "offensive" or "defensive," and it is a difficult human skill at times - like in many arguments - or discussions that derail into that.
Dickinson, also in the public domain, but I think Burnside's is more comprehensive. Here are
some gems you might find interesting:
1. Every equation of even degree and whose constant term is negative has at least two real
roots, one positive and one negative.
2. Every equation of odd degree has at least one real real root of sign opposite to that of
the constant term.
The classical formulas for the roots of equations of the third and fourth degree are
discussed as well as methods for finding intervals within which real roots must lie.
Although both books discuss iterative methods of finding roots, they omit Lagurerre's
Method, even though it was known at the time the books were written. This has remarkable
convergence properties and will even converge to a complex root.
I think that this material is interesting even though it is not as necessary as it was
before computer routines for solving equations became available.
Then you know everything I said, you just forgot it.Quote: puzzlenutI studied Galois from Galois's original paper.
Quote: teliotThen you know everything I said, you just forgot it.
I also studied groups and rings and Modern Algebra in 1978. I tend to remember parts of mathematics that I used more often in later life.
Defining a flat function is a smooth function ƒ : ℝ → ℝ all of whose derivatives vanish at a given point x0 ∈ ℝ.
For the flat function in the quote below, Doc asked the question as to what point they are trying to make when they say
f(x) is not equal to its Taylor series around the origin
Quote: WikipediaAnd even if the Taylor series of a function f does converge, its limit need not in general be equal to the value of the function f(x). For example, the function
f(x) = e^(-1/x^2) if x<>0 and 0 if x=0
is infinitely differentiable at x = 0, and has all derivatives zero there. Consequently, the Taylor series of f(x) about x = 0 is identically zero.
Quote: teliotThen you know everything I said, you just forgot it.
Evariste Galois (1811-1832) didn't use any of your terminology. I haven't found an online link to his paper, but it is quoted in several books. The only concept not in the standard mathematical vocabulary of his day was "groupe," and he didn't define it. You have to figure out from the context what he is talking about. Rings, fields, and all that came much later.
Quote: teliotLook up topics like Goedel's Incompleteness Theorem or the Banach-Tarski Theorem and get into some interesting conversations where there really is something to talk about. Or, when questions of infinity come up, don't talk about if "it exists" but rather discuss the cardinality of the rationals vs. the cardinality of the real numbers, Cantor's diagonal argument, and once that's understood, have a go at the Continuum Hypothesis.
Asking if a dog is a "dog" may be a Zen Koan, but it is not math.
There is no set whose cardinality is strictly between that of the integers and that of the real numbers.
That's interesting. I didn't realize that proving the theorem was a Hilbert problem.
In general, I think of everything not in terms of "existence" or "a mathematical model". For instance the statement "antimatter is matter travelling backwards in time" is a mathematical model. The statement is neither true or false. The relevant question is does it help in understanding the universe. The answer is an unqualified yes.
From Wikipedia, "The contributions of Kurt Gödel in 1940 and Paul Cohen in 1963 showed that the hypothesis can neither be disproved nor be proved using the axioms of Zermelo–Fraenkel set theory, the standard foundation of modern mathematics, provided ZF set theory is consistent."Quote: pacomartinThere is no set whose cardinality is strictly between that of the integers and that of the real numbers.
http://en.wikipedia.org/wiki/Continuum_hypothesis
When I was a professor at Ohio University, there was a faction of professors in the department (some world famous) who studied the topology of those infinities whose cardinality was properly between |Z| and |R|. They choose to add not-CH as an axiom to ZFC. This was fringe stuff, to be sure, but those guys sure took it seriously.
Quote: teliotThe word "imaginary" has nothing to do with what these numbers are, any more than the word "spot" has anything to do with the particular dog it names. It is just a historical accident that this word was chosen. Unfortunately, the name gives the appearance that there is some dispute. There is none. This number exists as much as any other number exists. "i" is the name of a number, it has no connection with the nature of the object itself, any more than "two" has anything to do with the object it refers to.
Sorry to wake up an old thread, but I keep knocking it around in my head from time to time. The quote above was regarding my asking if there is an i quantity of anything in the natural world.
My interpretation of what Eliot is saying is that no number really exists in a tangible way. If that is that case, may I propose the Wizard number w, which is defined as w4 = -1. Can I say that w is just as legitimate of a number as, say, 2?
Quote: paisielloCan't you just take the cube root of both sides so w = -1 ? which would be a simpler definition.
Good point. I don't seem to be at my best today. Let's define w then as w4=-1.
"Roots of unity" and are used all the time. The number w you refer to is a primitive eighth root of unity. The four distinct eighth roots of unity correspond to the complex numbers on the unit circle located at 45, 135, 225 and 315 degrees. You are not defining w, it already exists and can be written in the form a + bi, with a and b real numbers.Quote: WizardSorry to wake up an old thread, but I keep knocking it around in my head from time to time. The quote above was regarding my asking if there is an i quantity of anything in the natural world.
My interpretation of what Eliot is saying is that no number really exists in a tangible way. If that is that case, may I propose the Wizard number w, which is defined as w4 = -1. Can I say that w is just as legitimate of a number as, say, 2?
See: http://en.wikipedia.org/wiki/Root_of_unity
This article gives one of the explicit eighth-roots as an example:
w = (sqrt(2)/2)*(1 + i).
For this (and all) eight roots of unity, w^4 = -1.
Can you write out the other 3 eighth roots?
No, I am not saying this. I am saying that the names we attach to things that exist are arbitrary and have no relationship to the thing itself.Quote: WizardMy interpretation of what Eliot is saying is that no number really exists in a tangible way.
The questions whether mathematical concepts really exist and what it means for them to be true is from the philosophy of mathematics, which is a whole different direction of inquiry. One of the first questions that philosophers ask is "Does 2+2 = 4 on Mars?"
http://plato.stanford.edu/entries/fictionalism-mathematics/
Here are some excerpts:
Quote:2.2 Objectivity
A second objection to fictionalism is based on the idea that fictionalists cannot account for the objectivity of mathematics. It is an obvious fact about mathematical practice that there's some sort of objectivity at work in that practice. There's an important difference in mathematics between sentences like ‘2 + 2 = 4’ and ‘3 is prime’ on the one hand and ‘2 + 2 = 5’ and ‘3 is composite’ on the other. There's obviously some sense in which the first two sentences, but not the second two, are “correct”, or “right”, or “good”, or some such thing. The most obvious thing to say here is that the first two sentence are true whereas the latter two are false. But fictionalists cannot say this; they're committed to saying that all four of these sentences are untrue. Thus, the question arises whether fictionalists have any adequate account of the objectivity of mathematics—i.e., of the differences between these two kinds of sentences.
Quote:2.5 Accepting and Believing
As became clear in section 2.2, while fictionalists think that sentences like ‘2 + 2 = 4’ are strictly speaking false, they nonetheless think they're “correct” in some sense of the term. What, then, is the fictionalist's attitude toward these sentences? Following Bas van Fraassen (1980), who endorses a similar view with respect to empirical science, the standard fictionalist line here is that they accept sentences like ‘2 + 2 = 4’ without believing them. How exactly acceptance should be defined is a matter of some controversy, but one obvious way to proceed here is to claim that fictionalists accept a pure mathematical sentence S if and only if they believe that S is true in the story of mathematics.
Some people object to the distinction between belief and acceptance. Horwich (1991), O'Leary-Hawthorne (1997), and Burgess and Rosen (1997) present arguments for the claim that there is no real difference between acceptance and belief because, roughly, (a) to believe something is just to be disposed to behave in certain ways, and (b) those who believe that 2 + 2 = 4 and those who allegedly only accept that 2 + 2 = 4 are presumably disposed to behave in exactly the same ways.
Daly (2008) and Leng (2010) provide a number of responses to this argument. One point Daly makes is that fictionalists are in fact not disposed to behave in the same ways that platonists are. They're disposed to behave very differently in response to questions like, “Do there actually exist any such things as numbers?”


