Carpet Area Problem
February 10th, 2013 at 8:00:18 PM
permalink
A rug merchant is hired to carpet a hallway formed by two circular concentric walls. Not knowing the radii of the circles he has his men carry in a 20' stick to measure the circumference. Unfortunately when he gets it in the door and closes the door it is completely wedged between the outside wall (at the tips) and the inside wall. Even though he is unable to use the stick, he still knows how much carpet he needs.
How much carpet does he need?
How much carpet does he need?
February 10th, 2013 at 8:31:57 PM
permalink
To be clear two circular concetric walls is essentially a circular hallway.
I assume that the hallway is 20' thick. The amount of carpet required is
Let r be the radius of the outside circle.
The area of carpet is pi (r^2) - pi (r-20)^2 = pi(r^2 + 40r -400 - r^2 ) = pi(40r-400)
pi r^2 - pi (r-20)^2 = pi (-400 + 40r) where r is the radius of the outside wall.
I can't see how this can be solved without not knowing r. r > 20.
I assume that the hallway is 20' thick. The amount of carpet required is
Let r be the radius of the outside circle.
The area of carpet is pi (r^2) - pi (r-20)^2 = pi(r^2 + 40r -400 - r^2 ) = pi(40r-400)
pi r^2 - pi (r-20)^2 = pi (-400 + 40r) where r is the radius of the outside wall.
I can't see how this can be solved without not knowing r. r > 20.
-----
You want the truth! You can't handle the truth!
February 10th, 2013 at 8:45:11 PM
permalink
314.1593 sq ft
I heart Crystal Math.
February 10th, 2013 at 8:46:36 PM
permalink
Edit: recomputing....misunderstood the question the first time.
Quick answer: enough to cover the floor. ha ha.
Quick answer: enough to cover the floor. ha ha.
February 10th, 2013 at 8:55:02 PM
permalink
Crystal, how do you make that assumption?
-----
You want the truth! You can't handle the truth!
February 10th, 2013 at 9:09:02 PM
permalink
Quote: skrbornevryminrecomputing....misunderstood the question the first time.
Quick answer: enough to cover the floor. ha ha.
Ok. After having thought about this a little, I have determined that this cannot be solved with the information given, because we do not have the length of the hallway, only the width of it. At the very least it would be a circular room with the inner radius of 0' and the outer radius of 20 feet which is what I initially assumed. However, it could be a very long hallway such as that which would circle a basketball arena, for example, which was 20 feet wide.
Regardless of the area of the floor however, carpet comes off of a roll in rectangles (or squares) in most cases, so waste would be a factor as well. So until we get more info, I am sticking with my "quick answer" as stated above.
February 10th, 2013 at 9:19:03 PM
permalink
Crystalmath is correct. The area of the outer circle minus the area of the inner circle will always be equal to the area of a circle with a radius of 10'
February 10th, 2013 at 9:21:50 PM
permalink
Oh for heaven's sake. It's a carpet salesman. If he sent a stick that's 20 feet long he will tell you that you need 20 + 20 = 40 X 40 = 1600 square feet since carpet is sold in rectangular rolls, with a "liitle extra just in case you spill something later."
February 10th, 2013 at 9:57:11 PM
permalink
Quote: AlanMendelsonOh for heaven's sake. It's a carpet salesman. If he sent a stick that's 20 feet long he will tell you that you need 20 + 20 = 40 X 40 = 1600 square feet since carpet is sold in rectangular rolls, with a "liitle extra just in case you spill something later."
Of course. But if these problems happened to a real salesman, he'd use a tape measure rather than a stick.
Donald Trump is a fucking criminal
February 10th, 2013 at 10:18:17 PM
permalink
Quote: stargazerCrystalmath is correct. The area of the outer circle minus the area of the inner circle will always be equal to the area of a circle with a radius of 10'
I don't think so, because we do not know the diamater (or the radius) of the inner circle that the circular hallway goes around. (Imagine trying to carpet a circular racetrack around a circular field.) Since we don't know the length of the track, nor the diameter of the inner field, we cannot determine the area of the actual track itself. All we know is the width of the track, which isn't enough to compute the area of it.
I hope that I am not missing something...
February 10th, 2013 at 10:21:05 PM
permalink
I'm having a hard time visualizing the problem. Can anybody supply a drawing/diagram?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 10th, 2013 at 10:53:42 PM
permalink
The shaded area will always be pi * 10^2
February 11th, 2013 at 12:20:32 AM
permalink
Thanks. It changes the question, giving away Paco's answer, but we can still ask why this is true?
Draw a triangle with vertices (A) center of the circle, (B) edge of the chord, and (C) middle of the chord.
Let's call x the radius of the small circle and y for the large one.
The question is what is the area of the shaded region, which is pi* y<sup>2</sup> - pi*x<sup>2</sup>?
Via the Pythagorean Theorem, AB<sup>2</sup> = AC<sup>2</sup> + BC<sup>2</sup>
We know AB=y, and AC=x, so BC = sqrt(AC<sup>2</sup> + BC<sup>2</sup>).
We're also given from the drawing that BC = 10.
So pi * y<sup>2</sup> - pi* x<sup>2</sup> = pi*BC<sup>2</sup> = pi*100.
Let's call x the radius of the small circle and y for the large one.
The question is what is the area of the shaded region, which is pi* y<sup>2</sup> - pi*x<sup>2</sup>?
Via the Pythagorean Theorem, AB<sup>2</sup> = AC<sup>2</sup> + BC<sup>2</sup>
We know AB=y, and AC=x, so BC = sqrt(AC<sup>2</sup> + BC<sup>2</sup>).
We're also given from the drawing that BC = 10.
So pi * y<sup>2</sup> - pi* x<sup>2</sup> = pi*BC<sup>2</sup> = pi*100.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 11th, 2013 at 12:42:43 AM
permalink
There are two solutions:
1) Use a known formula to find the invariant.
2) A somewhat philosophical way to solve the problem is to
As an aside:
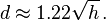
You may have seen that the approximate distance formula for the distance to the horizon (d in statute miles) and (h in feet). The approximation comes from a similar calculation. Given that the mast of an ancient ship was from a single large conifer tree (roughly 150' high), then you can see how the length of territorial waters was calculated (12 nautical miles from the beach). An international nautical miles is 6076' whereas a statute mile is 5280'.
1) Use a known formula to find the invariant.
Pythagorean
2) A somewhat philosophical way to solve the problem is to
assume that there is a solution (if the question was well posed). Under this assumption, then choose the most convenient inner diameter (i.e. the limit as it approaches zero). This solution might be called the "Gestalt solution". Once you know the answer you could proceed to the more formal solution #1.
As an aside:
You may have seen that the approximate distance formula for the distance to the horizon (d in statute miles) and (h in feet). The approximation comes from a similar calculation. Given that the mast of an ancient ship was from a single large conifer tree (roughly 150' high), then you can see how the length of territorial waters was calculated (12 nautical miles from the beach). An international nautical miles is 6076' whereas a statute mile is 5280'.
February 11th, 2013 at 12:47:44 AM
permalink
Quote: pacomartinThere are two solutions:
It is your thread, but may I suggest spoiler tags?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 11th, 2013 at 12:50:05 AM
permalink
Quote: stargazerThe shaded area will always be pi * 10^2
If it was an ordinary circle, this formula would also [of course] be the answer for the area of that circle with the 20 feet being the diameter. So it seems logical in a way; a tiny spot growing from the middle of a 20 foot diameter circle pushing against the 'rod', but allowing this original circle to grow so it keeps this one dimension, sort of does say the area of that circle can't decrease.
My drivel hardly the way to go about a mathematical proof.
btw no way could I get the question without this diagram.
the next time Dame Fortune toys with your heart, your soul and your wallet, raise your glass and praise her thus: “Thanks for nothing, you cold-hearted, evil, damnable, nefarious, low-life, malicious monster from Hell!” She is, after all, stone deaf. ... Arnold Snyder
February 11th, 2013 at 5:08:09 AM
permalink
For me, I thought the stick represented the width of the hallway. Now that I see the diagram it becomes more fun.
Crystal math's solution is correct
I don't know why
Crystal math's solution is correct
I don't know why
-----
You want the truth! You can't handle the truth!
February 11th, 2013 at 5:26:54 AM
permalink
Quote: odiousgambitSo it seems logical in a way; a tiny spot growing from the middle of a 20 foot diameter circle pushing against the 'rod', but allowing this original circle to grow so it keeps this one dimension, sort of does say the area of that circle can't decrease.
If you let R=radius of the outer circle, and r=radius of the inner circle then the area of the space between the circles is PI*(R2-r2). But the inscribed right triangle gives you r2+102=R2.
But what you are describing is an AHA moment (or Gestalt in German). Since you are assuming that I have not set you up with a problem with no answer, then by changing the size of the circles in your mind, the carpeted area grows thinner so that the area remains constant. In the limiting case where the inner diameter is nearly zero, the area approaches 100*PI.
Henri Poincaré, a famous mathematician, was very descriptive of the AHA moment. He said it was almost as if he didn't deserve credit for some of his discoveries. He was working on them very hard, and completely gave up and was doing something banal when the answer hit him.
February 11th, 2013 at 7:24:00 AM
permalink
What I want to know is why a carpet business doesn't have something so basic, cheap and simple to get as a tape measure.
Donald Trump is a fucking criminal
February 11th, 2013 at 3:03:42 PM
permalink
Reply to above.
Consider radius of the large circle to be "R" and the small one as "r". Consider the triangle from the midpoint of the stick to the outer wall. The base is 10, the height is "r" and the hypotenuse is "R". By Pythagoras R^2=r^2+100, so R^2-r^2=100.
The area of the large circle is Pi R^2. The area of the small circle is Pi r^2. The carpet needed is "large"-"small" = Pi R^2 - Pi r^2 = Pi (R^2 - r^2) = 100 Pi.
The area of the large circle is Pi R^2. The area of the small circle is Pi r^2. The carpet needed is "large"-"small" = Pi R^2 - Pi r^2 = Pi (R^2 - r^2) = 100 Pi.
