Evolution Lightning Blackjack

So online casinos are now offering an interesting variant of Live Blackjack called Lightning Blackjack. The RTP is pretty decent at 99.56%.

I am puzzled as to what optimal strategy to use. For example, if I have a high multiplier going and then I get a 10 against a dealer 8, normally I would double down. However, as a win would achieve the multiplied payout, would it not be safer to just hit, so if I got a 2 (say) making 12, I could then hit again?

I would love to know how to play this game perfectly so as to minimize the house edge, but surely a sophisticated calculator would be required.

Additionally, I wonder if the advertised 99.56% RTP applies to just playing basic strategy or with perfect play.

Any insights would be appreciated.

Quote: bustamove

So online casinos are now offering an interesting variant of Live Blackjack called Lightning Blackjack. The RTP is pretty decent at 99.56%.

I am puzzled as to what optimal strategy to use. For example, if I have a high multiplier going and then I get a 10 against a dealer 8, normally I would double down. However, as a win would achieve the multiplied payout, would it not be safer to just hit, so if I got a 2 (say) making 12, I could then hit again?

I would love to know how to play this game perfectly so as to minimize the house edge, but surely a sophisticated calculator would be required.

Additionally, I wonder if the advertised 99.56% RTP applies to just playing basic strategy or with perfect play.

Any insights would be appreciated.
link to original post

I guess you should find the win/tie/loss probability for DOUBLE and HIT, from there you can calculate either DOUBLE or HIT will give higher return.

I'm not exactly sure what the multiplier rule is but I have seen a promotion that pays 2 to 1 on any wins (only on first hand doubles but not splits), alternatively think the strategy on free-bet where you can win twice without risking more money. In the latter you free-bet double 9 vs A, split all 4-4, etc! I think if you're being paid 2 to 1 then you double things like 13 vs 6!

You can create a(n infinite) spreadsheet using 2 to 1 instead of 1 to 1 using EVs which are Pr(Win) * 2 - Pr(Lose) * 1 without worrying about the ties too much, by and large why wouldn't you pile more money on if you're being paid great odds. If you're only being paid tasty odds on the original bet then sometimes you'll play safe (split more, double less, stand earlier) and other times hit more (e.g. 17 vs 7) c.f. freebet.

Quote: bustamove

So online casinos are now offering an interesting variant of Live Blackjack called Lightning Blackjack. The RTP is pretty decent at 99.56%.

I am puzzled as to what optimal strategy to use. For example, if I have a high multiplier going and then I get a 10 against a dealer 8, normally I would double down. However, as a win would achieve the multiplied payout, would it not be safer to just hit, so if I got a 2 (say) making 12, I could then hit again?

I would love to know how to play this game perfectly so as to minimize the house edge, but surely a sophisticated calculator would be required.

Additionally, I wonder if the advertised 99.56% RTP applies to just playing basic strategy or with perfect play.

Any insights would be appreciated.
link to original post

The good news is that the game has a decent RTP and the bad news is that, "Perfect Strategy," is going to be very difficult to come by.

The way that I understand the rules is this:

1.) The player will make a bet on an ordinary Blackjack hand (base bet) and then will pay a, "Lightning Fee," equivalent to that bet.

2.)The Lightning Fee will enable a player to generate multipliers for reaching certain hand totals which are somewhat randomly assigned before the player takes any action.

3.) If the player wins the current hand, then the player will get the multiplier corresponding to the player's hand total for the following hand. If the player wins the following hand, then the player will be paid the Lightning Fee amount from the previous hand multiplied by the multiplier.

With that, I have a question:

Since the Lightning Fee is paid the prior hand, do you have to make the same bet amount (and Lightning Fee) for the following hand? I'm sure if you bet more, then that just means that you would pay a greater Lightning Fee, but any win on the multiplier will be based on the previous hand---so no need to do that. My theory with betting less (if the pay will be based on the amount bet the previous hand) is that it will lessen the impact (base game) of making strategy deviations in an effort to just win the hand.

For now, I will assume the bet amount is the same, so let's look at our variables on this thing:

1.) What would normally be the best decision?

2.) What are the potential multipliers to be earned for the following hand?

3.) What, if any, is the multiplier active on the current hand?

With that, let's use your example of a 10 against a dealer 8 and compare the two, for this, we will say you already have a multiplier active:

Decks: 8
Dealer Peeks: Yes
Soft 17: Stand
Double Down: Any First Two
Split: Yes
Hit Split Aces: No
Blackjack: 3:2

Okay, so normally with a player ten v. a dealer showing 8 (I made it 6-4 for the player) we would have the following:

Surrender: -.5
Stand: -0.513156
Hit: +0.199206
Double: +0.290356

https://wizardofodds.com/games/blackjack/hand-calculator/

Personally, I don't think this hand is going to be particularly close in terms of changing the decision to double. For that reason, I'm going to change your example hand to something a little closer, a hand total of ten v. a dealer nine:

Surrender: -.5
Stand: -0.543320
Hit: +0.116689
Double: +0.146896

With that, we are going to go to this calculator:

https://www.beatblackjack.org/en/strategy/dealer-probabilities/

What that calculator does is it tells us final hand probabilities for the dealer based on what's left in the shoe and the dealer's upcard. What we see is the following for a dealer starting with 9 and a 6 and 4 also gone from the shoe:

Bust: .229
21: .061
20: .12
19: .354
18: .116
17: .121

SUM: 1.001 (Rounding, I assume)

Okay, so we can break this down into win probability and loss probability conditions with doubling somewhat easily. With your total of ten, there are five ranks (2,3,4,5,6) that would result in a hard total on a double that cannot compete with a made dealer hand. For those, we can just use the probabilities above. We have already removed a 4 and a 6 from the deck, and the dealer's nine is also gone, so there are 413 cards remaining of which 158 are the applicable ranks.

If the dealer busts, you win...if the dealer doesn't bust, then you lose. We are not concerned with overall EV at this time as that has already been calculated for us, so we are only concerned with the probability of winning the hand:

(158/413) * .229 = 0.08760774818---NOTE, Effect-of-Removal would still play a factor, but we can't know what we are removing ahead of time and it's negligible anyway.

With that, you will double and make a hand total of 12-16 8.760774818% of the time and still win due to the dealer busting.

Our next concern is doubling to a hand total of 17 and winning, pushes lose for the purpose of the Lightning Fee, so the only thing we care about for win probability is getting to 17 and the dealer busting:

(32/413) * .229 = 0.0177433414

With that, you will double to 17 and produce a winning hand roughly 1.77433414% of the time.

The next possibility is that you receive an 8, which will beat either a bust or a dealer total of 17 as follows:

(32/413) * (.229 + .121) = 0.02711864406

With that, that result will come to pass 2.711864406% of the time.

The next possibility is that you receive a 9, which will beat Dealer Bust, Dealer 17 and Dealer 18

(31/413) * (.229 + .121 + .116) = 0.03497820823

With that, we will see such a result 3.497820823% of the time.

The next possibility is that you receive a ten, which will beat everything except a dealer twenty or dealer twenty-one:

(128/413) * (.229 + .121 + .116 + .354) = 0.25414043583

With that, we see that this result will happen about 25.414043583% of the time. It's actually slightly less because you have removed a ten from the deck, which makes a dealer total of 19 slightly less likely, but I'm not trying to be perfect here and it's negligible to illustrate the point.

Finally, the player might receive an Ace for a total of 21. That beats all dealer hands and only pushes if the dealer finishes with 21, as well:

(32/413) * (1-.061) = 0.07275544794

With that, we get a win probability of 7.275544794%.

We will now sum up our win probabilities:

8.760774818%+1.77433414%+2.711864406%+3.497820823%+25.414043583%+7.275544794% = 49.434382564%

You might be wondering why we double if that is not at least 50%, but remember, we did not do any math for pushes as they have already been factored into the EV calculations to begin with.

The next thing that we have to do is calculate the probabilities for the player's total on the assumption that the player does not double to get a win probability. While that might sound difficult, it's actually going to be pretty easy because the player will effectively follow the same rules that the dealer does for the remainder of the hand---hit until he reaches a total of 17, or greater. With that, the work is already done for us as we can use the chart that has the probabilities of final hand totals for a dealer starting showing a ten:

Bust: .212
21: .035 + .077
20: .339
19: .112
18: .112
17: .112

(For simplicity, I only removed a ten from the deck for this)

For the 21, the dealer chart has 7.7% for Blackjack, so I had to add that back in as if the player draws an ace to a total of ten.

Okay, so now we do the same thing. Seventeen only wins if the dealer busts:

(.112) * .229 = 0.025648

Player 18 Beats Dealer 17 and Bust:

(.112) * (.229 + .121) = 0.0392

Player 19 Beats Dealer Bust and 17-18:

(.112) * (.229 + .121 + .116) = 0.052192

Player 20 Beats Dealer Bust and 17-19

(.339) * (.229 + .121 + .116 + .354) = 0.27798

Player 21 Beats All Except Dealer 21:

(.112) * (1-.061) = 0.105168

With that, we sum up our win probabilities:

0.105168+0.27798+0.052192+0.0392+0.025648 = 0.500188

BRINGING IT HOME

Okay, so the example that we ended up using was that of a player total of 10 v. a dealer showing 9 because that is a much closer decision to hit or double on an EV basis.

DISCLAIMER: I know I have already said it, but I want to make very clear that the probabilities above should be taken as a ROUGH ESTIMATION as I did not account for Effect-of-Removal as it would have required me to account for every possible series of player hits (to hand totals) and dealer results individually...and, while I'm capable of doing it, I'm not really inclined to do it for free. Someone could probably write a program to do it much faster, anyway.

The first thing that we will do is go back to our base EV:

Surrender: -.5
Stand: -0.543320
Hit: +0.116689
Double: +0.146896

With that, we will next look at the win rates:

Double: .49434382564

Hit: 0.500188

Even then, it's a bit convoluted for three reasons:

1.) We need to win in order to get the value from the current hand multiplier.

2.) We need to win in order to get a multiplier for the hand after this one.

3.) We have made the Lightning Fee bet again, so we will lose that if we do not win this hand.

For that reason, we must now treat the two bets separately, in terms of EV. We already have our EV for the base game, so now we have to figure out our EV for the Lightning Bet...but we are going to ignore the second point (the multiplier for the following hand) for simplicity---this is mainly because these multipliers offered are not only random, but are also higher based on the higher the hand total is. Going the route of hitting, as opposed to doubling, we are slightly more likely to finish with higher hand totals.

Based on just winning the hand:

Hit: 0.500188
Double: .49434382564

The inverse of these will represent the probability of losing or pushing the hand, which will cause our current Lightning Fee to be lost as well as the Lightning Fee that we paid the previous hand for the current multiplier. That will be a loss of two units, so these must be multiplied accordingly:

((1-.500188) * -2) = -0.999624

((1-.49434382564)*-2) = -1.01131234872

Both of those numbers represent our -EV from Losing the hand as it will cause both the previous Lightning Fee and the current one to be lost as the player would receive zero return on either.

1.01131234872 -0.999624 = 0.01168834872

From that perspective, hitting is better than doubling by .01168834872 units before you even get into possible win. Let's look again at our EV's for each decision based on a normal Blackjack hand:

Surrender: -.5
Stand: -0.543320
Hit: +0.116689 + 0.01168834872 = 0.12837734872
Double: +0.146896

With that, we see the added EV of hitting (for the Lightning Bet) brings the two closer. Let's see how much of a difference there is between the two:

0.146896-.12837734872 = 0.01851865128

Okay, so per multiple, the difference in the winning rates will also be the difference in per unit EV:

Hit: 0.500188 Double: .49434382564 (.500188-.49434382564) = 0.00584417436

In this case, if we had a 4x multiplier, we would see: 0.00584417436 * 4 = 0.02337669744

That, taken together, hitting and maximizing the probability of winning the hand becomes the better decision when you are looking at both bets total expected outcome. The difference in the EV Loss on the base hand of hitting as opposed to doubling has been overcome by the EV gain of maximizing the probability of winning on this particular hand.

I would say that we can also be pretty sure of that because we didn't even factor in the multiplier value for the following hand, which we would also receive if we won the current hand. Depending on the probability of achieving certain results, and what the multipliers for the following hand might be, this could become the correct decision at a multiple for the current hand of 3x, but I have no idea and it would be ridiculous to even try to figure out.

My advice is not to play this if there is a standard Blackjack game with the same House Edge, or lower. At some point, you'll be put into situations where you must sacrifice the EV of one aspect of the hand in order to satisfy the other aspect for the best overall EV. It would also be crazy difficult to calculate all of them because of all the different situations that can come up with hand results, current multipliers and potential future multipliers...which would all be a factor every time.

In fact, the potential for future multipliers (if they are really high) might even be enough to try to maximize the probability of winning (or even just trying to achieve a particular multiplier) for hands that don't even currently have a multiplier.

For example, if you skip to 17:27 of this video:

https://www.youtube.com/watch?v=16ok5a-Aoq8

Imagine if the player ended up with a hand total of hard 13 against a dealer two. Base hand EV favors standing, so by necessity, so do the win probabilities...but the difference isn't astronomical and you have potential multipliers for the following hand that could become a consideration.

My conclusion is that this game is a total mess that nobody should play and optimal strategies for the game would require the following charts:

1.) An optimal strategy for hands with no current multiplier available that is based not only on the base EV, but also, on all of the potential multipliers that are available for the following hand. You obviously couldn't really have a chart like that because of how many possible combinations there might be, so you'd probably have to create a calculator that does this.

2.) An optimal strategy based on hands that currently do have a multiplier that either does, or does not, also include the potential multipliers that are available for the next hand.

It doesn't appear that Surrender is available, but if it was, you would never do it. You would be forfeiting 1.5 units as you would lose the Lightning Bet and could not receive a multiplier for the next hand.

ADDED: At a certain point, I think Doubling 10 v. Dealer 8 might change to a hit with a very high multiplier, but I did Player 10 total v. Dealer 9 instead because I was pretty confident there would come such a point.

I just found this thread. I think I can analyze this one by modifying a current blackjack spreadsheet. However, first let me let explain the gist of the game. The game is based on conventional blackjack rules. I shall assume the rules posted above are correct. However, if the player pays a non-refundable fee equal to the original bet, then any win shall be multiplied by a posted multiplier. I've been watching Glen's video and have these recorded so far:

Hand	4 to 17	18	19	20	21	BJ
1	2	3	4	5	6	8
2	2	4	5	6	10	15
3	2	3	4	5	6	8
4	2	4	5	6	10	15
5	2	3	4	5	6	8

Note that so far it's been the set of two alternating.

Stay tuned for more information.


Direct: https://www.youtube.com/watch?v=16ok5a-Aoq8

I wrote an article on this game that can be found here:

https://wizardofvegas.com/article/ultimate-x-blackjack/

The title is, "Ultimate X Blackjack," just as a play on the concept of the game.

It offers some other theories of where strategy might change and also theorizes about countability. While the shoe penetration of this game sucks, it occurs to me that Naturals and other high hand totals (which correlate to a positive count anyway) have even greater value because of the higher average multiplier associated with them. Therefore, intuitively, the True Count needed to be at an advantage should go down...but I couldn't even begin to know by how much.

For Wizard, I already found all the multipliers from this video for a Natural Blackjack...so I can say that it doesn't go back and forth the entire time. Natural Blackjack went:

Quote: Article

8x, 15x, 8x, 15x, 8x, 6x, 8x, 12x, 6x, 6x, 20x, 15x, 15x, 8x, 6x, 12x, 6x, 12x, 6x

The average for that sample is 10.105x multiplier if the hand is won.

So, unfortunately, getting an average won't be very easy...unless you can E-Mail them and they will just tell you or it is in the game rules. I have access to at least one online casino with this game (I think) so I can check if you want.

I finished watching Glen's video and recorded 19 hands. Here are the multipliers in each of them. The first column is a time in the video this hand appears.

Hand	4 to 17	18	19	20	21	BJ
0:54	2	3	4	5	6	8
2:15	2	4	5	6	10	15
3:59	2	3	4	5	6	8
5:38	2	4	5	6	10	15
6:36	2	3	4	5	6	8
7:36	2	2	3	4	5	6
9:27	2	3	4	5	6	8
11:11	2	3	4	5	8	12
12:44	2	2	3	4	5	6
15:01	2	2	3	4	5	6
17:20	2	5	6	8	12	20
20:02	2	4	5	6	10	15
21:32	2	4	5	6	10	15
22:33	2	3	4	5	6	8
23:22	2	2	3	4	5	6
27:11	2	3	4	5	8	12
28:48	2	2	3	4	5	6
29:50	2	3	4	5	8	12
31:38	2	2	3	4	5	6
Average	2	3	4	5.05	7.16	10.11

Wizard,

I just checked the Unibet app as their Blackjack is powered by Evolution Gaming, but Lightning Blackjack doesn't seem to be on the PA Unibet yet. Waste of five minutes waiting for their app to open and then another ten waiting for Live Tables to load...lol...their app leaves a bit to be desired in loading times, though the stability is great once you finally have loaded a game.

Quote: Mission146

Wizard,

I just checked the Unibet app as their Blackjack is powered by Evolution Gaming, but Lightning Blackjack doesn't seem to be on the PA Unibet yet. Waste of five minutes waiting for their app to open and then another ten waiting for Live Tables to load...lol...their app leaves a bit to be desired in loading times, though the stability is great once you finally have loaded a game.
link to original post

Thank you.

I was wondering what was to prevent a player from betting small with no multiplier and big with a large one. According to Live Casino Comparer, the multiplier applies only up to the amount bet in the hand it was earned. Anything bet above that is paid at standard odds.

This game is like getting a push for two pairs in video poker.

Quote: Wizard

Thank you.

I was wondering what was to prevent a player from betting small with no multiplier and big with a large one. According to Live Casino Comparer, the multiplier applies only up to the amount bet in the hand it was earned. Anything bet above that is paid at standard odds.
link to original post

That's correct. It's basically a two-step process by which the multiplier for the next hand is awarded based on winning the prior hand, so it is based on the amount bet the prior hand. That makes sense, otherwise, people could crush this game.

The way I understood it from Live Casino Compare is that, if you bet less on the following hand than the hand that earned the multiplier, once again, the multiplier will pay based on the lesser of the two bets.

That's actually kind of unfortunate because otherwise people could earn a multiplier with the big bet and then play a much smaller bet so that any deviations from Optimal Strategy (to maximize the probability of winning) wouldn't take so much away from making the right decision on the base game.

Quote: ChumpChange

This game is like getting a push for two pairs in video poker.
link to original post

I still think Ultimate X is the closest comparison. The only difference is the payout is based on the Lightning Fee paid and not total amount won.

I can see a possible way to approach this but only based on infinite decks and a general assumption of what the next hand might look like.

For the first hand we need to know the value of this round's BJ bet, the value of winning this hand and passing on a specific multiplier to the next hand.

For the next hand we need to know the value of that round's BJ bet (same as above), the value of the bonus pay-out based on the multiplier coming in, the value of the next hand's fee bet (we can only guess at the next hand's multipliers).
Combine the EVs at each decision point to generate a revised strategy and the value of coming into the next hand with a specific multiplier.

Use the next hand values to establish the value of the various totals on the first hand and work out the strategy.

For each of the above generate a spreadsheet which gives the basic EVs of various player decisions vs all possible dealer up-cards (Hit, Stand, Double, Split) (assuming you never surrender or take even money). Add together the EVs and create a combined strategy.

NB I haven't done any calculations except the probabilities of the dealer's hands (infinite) this but let's say getting 21 has an EV of 2.5 for the effect of handing over a multiplier to the next hand, then interestingly you might hit 17 vs 7, and you wouldn't double 11 and 10; the reason is getting 21 and 20 have such high values worth shooting for.
(Personally I think carrying over a multiplier from a winning 21 is higher than this, but it shows that sometimes you may need to go for those to get the big payoffs.)

Note: I have not worked out the value of handling over various multipliers, also the actual values will vary from hand to hand. This just assumed the multipliers were 7x 5x 4x 3x 2x, the worth was proportional to the multiplier, and factoring in the chance of winning the hand on your total. The object is to show, using a conservative estimate, how it might be worth considering not doubling and hitting more aggressively.

Player Total	EV St Base	EV St Ante	Combined St EV	Combined Hit EV
21	.925 926	2.500 000	3.425 926	.000 000
20	.773 227	1.634 080	2.407 307	.263 533
19	.615 976	1.185 956	1.801 933	.448 710
18	.399 554	.730 016	1.129 571	.587 320
17	-.106 809	.202 355	.095 546	.674 210
16	-.475 375	.202 355	-.273 020	.723 378
15	-.475 375	.202 355	-.273 020	.782 216
14	-.475 375	.202 355	-.273 020	.841 990
13	-.475 375	.202 355	-.273 020	.906 833
12	-.475 375	.202 355	-.273 020	.976 622
11	-.475 375	.202 355	-.273 020	1.842 385
Double 11				1.541 027
10	-.475 375	.202 355	-.273 020	1.343 537
Double 10				1.328 291

That's some pretty incredible work already, CharliePatrick. I figured I'd try to give this game a little more attention so that better minds than mine (such as yours, Wizard's and perhaps Teliot's and others) could take a stab at figuring this bad boy out.

In theory, I could figure this out, but the only way that I know how would take forever because it would be to analyze every possible decision point and possible series of results of one decision v. another by hand. Even the 10 v. Dealer 9 that I did (Double v. Hit) took a lot of shortcuts, though I'm pretty confident (Hit if 4x multiplier, or greater, for the current hand) is correct. It might even be a multiplier of 3x, depending on what the multipliers that are available for the next hand (if this hand is won) are.

Let's consider 9,8 v 6
Active Multiplier = 20
Upcoming mulitpliers = lowest paytable (2,2,3,4,5,6)
This makes some crude calculations as to the additional value on the upcoming hand if you get a specific multiplier.
As you can see, the values are very close, and only slightly favor standing. However, if you are playing for a higher set of future multipliers, this will flip so that you will double.

Given a high enough active multiplier and future multipliers, you will double hard 17 v 6.

The first table is for standing

Total	p(win this total)	Win	Added EV for Multiplier Next Hand	Contribution
17	0.421500182		0.4	0.168600073
18	0		0.4	0
19	0		1	0
20	0		1.5	0
21	0		2.2	0
BJ	0		3	0
p(win)	0.421500182	20		8.430003642
p(lose)	0.41233857	-1		-0.41233857
p(push)	0.166161248	0		0
				8.186265144

The second table is for Doubling

Winning Total	Probability	Win	Added EV for Multiplier Next Hand	Contribution
17	0		0.4	0
18	0.045442856		0.4	0.018177143
19	0.053750286		1	0.053750286
20	0.062023491		1.5	0.093035236
21	0.069925159		2.2	0.153835351
BJ	0		3	0
p(win)	0.231141793	40		9.245671708
p(lose)	0.736843198	-2		-1.473686396
p(push)	0.032015009	0		0
				8.090783328

Good stuff, Crystal and Charlie.

I've spent much of the day on a simulator for this game, based on blackjack basic strategy. I already suspect proper strategy is very dependent on the multiplier earned the previous hand.

If either of you or any other qualified person feels they are comfortable with a full analysis of this, I would be interested in publishing it on WoO. Not only would I give full credit and a link to any business interest you may have, but might pay a little something too. Not enough to make it worth your time, but hopefully enough for a nice dinner.

Let me know by PM if you're interested.

Quote: CrystalMath

Let's consider 9,8 v 6
Active Multiplier = 20
Upcoming mulitpliers = lowest paytable (2,2,3,4,5,6)
This makes some crude calculations as to the additional value on the upcoming hand if you get a specific multiplier.
As you can see, the values are very close, and only slightly favor standing. However, if you are playing for a higher set of future multipliers, this will flip so that you will double.

Given a high enough active multiplier and future multipliers, you will double hard 17 v 6.

The first table is for standing

Total	p(win this total)	Win	Added EV for Multiplier Next Hand	Contribution
17	0.421500182		0.4	0.168600073
18	0		0.4	0
19	0		1	0
20	0		1.5	0
21	0		2.2	0
BJ	0		3	0
p(win)	0.421500182	20		8.430003642
p(lose)	0.41233857	-1		-0.41233857
p(push)	0.166161248	0		0
				8.186265144

The second table is for Doubling

Winning Total	Probability	Win	Added EV for Multiplier Next Hand	Contribution
17	0		0.4	0
18	0.045442856		0.4	0.018177143
19	0.053750286		1	0.053750286
20	0.062023491		1.5	0.093035236
21	0.069925159		2.2	0.153835351
BJ	0		3	0
p(win)	0.231141793	40		9.245671708
p(lose)	0.736843198	-2		-1.473686396
p(push)	0.032015009	0		0
				8.090783328

link to original post

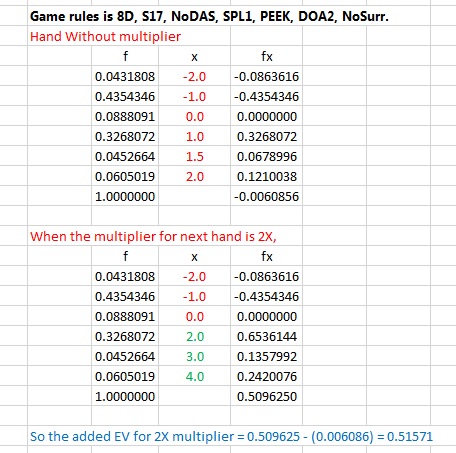
The game rules is 8D, S17, NoDAS, SPL1, PEEK, DOA2, NoSurr.

How do you get the Added EV for Multiplier Next Hand, 0.4, 0.4, 1.0, 1.5, 2.2, 3.0 ?

When multiplier is 2X, my estimated additional EV is 0.51571 as shown below. Where did I go wrong? How do you get 0.4 ?

I had assumed when you doubled, with no incoming multiplier, the value of the bet for the carry over would remain at the original bet. As I haven't played the game I don't know whether if you have an incoming multiplier and then double, whether the doubled wager is paid x1 or the multiplier (perhaps the rule if you increase your bet only the original bet is multiplied could apply). If the doubled value is paid the multiplier then you will be doubling more often, e.g. some stiff hands; I haven't looked but under some circumstances you might just double almost anything.

Similarly if you split there was a comment that it only paid out on the best hand, or was this for the multiplier that carried forward. Again you might just split everything (except 5s and 10s) and if you already had 20 on the first hand might be less aggressive on the second (since only getting 21 is of any benefit).

Quote: charliepatrick

I had assumed when you doubled, with no incoming multiplier, the value of the bet for the carry over would remain at the original bet. As I haven't played the game I don't know whether if you have an incoming multiplier and then double, whether the doubled wager is paid x1 or the multiplier (perhaps the rule if you increase your bet only the original bet is multiplied could apply). If the doubled value is paid the multiplier then you will be doubling more often, e.g. some stiff hands; I haven't looked but under some circumstances you might just double almost anything.

Similarly if you split there was a comment that it only paid out on the best hand, or was this for the multiplier that carried forward. Again you might just split everything (except 5s and 10s) and if you already had 20 on the first hand might be less aggressive on the second (since only getting 21 is of any benefit).
link to original post

-deleted-

Quote: charliepatrick

I had assumed when you doubled, with no incoming multiplier, the value of the bet for the carry over would remain at the original bet. As I haven't played the game I don't know whether if you have an incoming multiplier and then double, whether the doubled wager is paid x1 or the multiplier (perhaps the rule if you increase your bet only the original bet is multiplied could apply). If the doubled value is paid the multiplier then you will be doubling more often, e.g. some stiff hands; I haven't looked but under some circumstances you might just double almost anything.

Similarly if you split there was a comment that it only paid out on the best hand, or was this for the multiplier that carried forward. Again you might just split everything (except 5s and 10s) and if you already had 20 on the first hand might be less aggressive on the second (since only getting 21 is of any benefit).
link to original post

I think this video can answer most of your questions.

https://www.youtube.com/watch?v=16ok5a-Aoq8

Quote: ssho88

link to original post

The game rules is 8D, S17, NoDAS, SPL1, PEEK, DOA2, NoSurr.

How do you get the Added EV for Multiplier Next Hand, 0.4, 0.4, 1.0, 1.5, 2.2, 3.0 ?

When multiplier is 2X, my estimated additional EV is 0.51571 as shown below. Where did I go wrong? How do you get 0.4 ?


link to original post

Mine was a very quick estimate. I do need to point out that the blackjack on the next hand will pay 2, not 3. On the base hand, blackjack pays 1.5, but on a multiplier hand, it pays the multiplier.

Also, you will get less EV out of a lower multiplier hand because you will be more likely to aim for higher multipliers at the risk of busting more often. On a high multiplier hand, you'll get a higher EV because of doubles and splits.

So anybody gonna run a progression on a winning streak, like $10 + $10, $15 + $15, $20 + $20, $30 + $30, $40 + $40, $50 + $50, $75 + $75, $100 + $100?

Quote: charliepatrick

As I haven't played the game I don't know whether if you have an incoming multiplier and then double, whether the doubled wager is paid x1 or the multiplier (perhaps the rule if you increase your bet only the original bet is multiplied could apply). If the doubled value is paid the multiplier then you will be doubling more often, e.g. some stiff hands; I haven't looked but under some circumstances you might just double almost anything.

I think only the original wager gets multiplied if you double. The doubled portion of the bet would pay even money.

Quote:

Similarly if you split there was a comment that it only paid out on the best hand, or was this for the multiplier that carried forward. Again you might just split everything (except 5s and 10s) and if you already had 20 on the first hand might be less aggressive on the second (since only getting 21 is of any benefit).
link to original post

I'd like to get the splitting rules confirmed too.

Another thread was created about Lightning Blackjack. Several posts were made before I closed it. Let me reply to one of them.

Quote: CrystalMath

Double down pays 2x multiplier. Splits pay multiplier on each hand.
link to original post

I'm not saying you're wrong, but can you quote anything as evidence? Live Casino Comparer says, "Only the value of the Lightning Fee is multiplied." I interpret that to mean that if you double, then only the original wager is subject to the multiplier and the double portion pays the normal even money. Of course, I could be reading it wrong or that site may be wrong. Just looking for something more concrete to base my rules on when I write about the game, which will be soon.

I've just sent them this e-mail (via this pagehttps://www.evolution.com/our-games/lightning-blackjack ), before noticing the other thread is now closed as a duplicate. It would be great to have a clear understanding on (d) and (e).

Quote: email

There has been some discussion about your game on wizardofvegas forum and, as it's fun, I've had a quick look at it; some of the decisions are likely to be non-obvious. However there seems to be some discussion over the exact rules. Please forgive me or could I ask whether you either have a game card or could clarify some of the questions being raised.

Base assumptions
For analysis purposes the player makes two equal bets and will stick to those for subsequent hands (while they don't have to, that seems the optimal strategy).
The game is based on US rules "8D, S17, NoDAS, SPL1, PEEK, DOA2, NoSurr." and when doubling or splitting there is no additional "Ante" wager required.

Multiplier assumptions
(a) The multiplier passed forward to the next hand is solely based on the higher of the two hand values if the hand has been split.
(b) There have been estimates on the average value of the multipliers (I imagine this is commercially sensitive so would not expect you to comment on that!)
(c) A winning blackjack receives the multiplier rather than 6/4.

Questions The uncertainty is on multiplied hands which split or double.
(d) Where the original hand was a pair and has been split (and hence cannot be doubled) the multiplier applies to both hands, or is it just the first one?
(e) Where the original two-card hand was doubled it is not clear whether the multiplier applies to the original wager or includes the double part (e.g. 7x, $5 doubled would payout $35+$5 or $35+$35).

Clearly the first hand ever played cannot "return" 99.56% since the "Ante" wager is not returned and can only take effect when the following hand is played; however any multiplier earned will have a financial value, so this can be calculated and added for EV purposes.

Many thanks

To add to the confusion about the rules, Live Casino Comparer states both:

1. "If you lose, the Lightning Fee and the main bet are lost."
2. "In the case of a push or insurance, the player gets his main bet back but loses the Lightning Fee."

This seems to imply, by omission, that if the player has a multiplier from the previous hand and wins, then he gets the Lightning Fee back.

After a careful watching of Neil's video, this does not happen.

As evidence, note at the 12:07 point he just won a hand and has a balance of $376.14 (forgive me for using the dollar sign, he was betting in UK pounds) and earned a 4x multiplier. He then bets $5 the next hand. You can see his balance drop by $10 after the bet is made to $366.14 ($5 for the main wager and $5 for the Lightning Fee).

He wins that second hand. After being paid, his net win is $15. He win 4*$5 = $20 for beating the dealer, but $5 is deducted for the Lightning Fee. Neil explains it at the 14:23 point.

To address splitting, at the 19:19 point Neil splits sixes and you can see a 3x multiplier is applied to both hands. Unfortunately, he draws to a 16 on both and then loses, so that doesn't shed any light on the question of what happens if you win on two different totals.

Quote: Wizard

To address splitting, at the 19:19 point Neil splits sixes and you can see a 3x multiplier is applied to both hands. Unfortunately, he draws to a 16 on both and then loses, so that doesn't shed any light on the question of what happens if you win on two different totals.
link to original post

(Quote clipped, relevance)

You would be awarded the Lighting Fee for the previous hand (if any) multiplied by the multiplier once. As far as the multiplier for the following hand is concerned, it would be based on the higher of the two hand totals.

I have started a new page on Lightning Blackjack. So far, it has an introduction and rules only.

I welcome any corrections.

I'd throw in the drinks! 😉

Thanks everyone for your contributions so far, and sorry Wiz for not realizing this thread already existed.

My luck on this game was so atrocious that I've never even seen a payout with an active multiplier. But I'll give it another go with far lower stakes later.

I did want to make sure the thread is aware of Evolution's peculiar peek policy, which I confirmed this game uses (at least the dealer confirmed in chat). They peek with A showing, but not with face/10 showing.

Quote: Wizard

I have started a new page on Lightning Blackjack. So far, it has an introduction and rules only.

I welcome any corrections.

Thanks for putting this together, Wiz. I'll try to confirm the double payouts later.

I also saw in the documentation the claim that the maximum multiplier is actually 25x. I haven't seen it myself but I'll holler if I run into it. I can contribute to your multiplier samples.

Quote: Wizard

I have started a new page on Lightning Blackjack. So far, it has an introduction and rules only.

I welcome any corrections.
link to original post

I think Evloution's website comes close to confirming the rule that pays are on the Lightning Fee only:

https://www.evolution.com/our-games/lightning-blackjack

Quote:

In Lightning Blackjack players are always guaranteed a randomly generated multiplier of between 2x and 25x on a winning score. If the player’s hand wins, they will receive a multiplier of either 2x, 5x, 8x, 10x, 15x, 20x or 25x.

The multiplier is saved for the next game round, and the payout is increased by this multiplier if the player wins in that next round.

If players have to leave the game before getting a chance to play their awarded multiplier, that’s not a problem – the multiplier remains available for them to use for up to 180 days.

You'll notice that the verbiage says, "...and the payout is increased by this multiplier if the player wins in that next round," so my tendency is to think that is always Lightning Fee (previous hand) amount * multiplier added to base game winnings. Otherwise, I would think that the verbiage would be, "Any winnings are multiplied by your multiplier total in the next round."

Quote: Glunn11

Quote: Wizard

I have started a new page on Lightning Blackjack. So far, it has an introduction and rules only.

I welcome any corrections.

Thanks for putting this together, Wiz. I'll try to confirm the double payouts later.

I also saw in the documentation the claim that the maximum multiplier is actually 25x. I haven't seen it myself but I'll holler if I run into it. I can contribute to your multiplier samples.
link to original post

It is 25x maximum, Evolution's site says so.

Quote: Glunn11

I did want to make sure the thread is aware of Evolution's peculiar peek policy, which I confirmed this game uses (at least the dealer confirmed in chat). They peek with A showing, but not with face/10 showing.
link to original post

Thank you.

In Neil's video at one point the dealer has a 10 up, he plays his hand, and then the dealer reveals a blackjack.

RE: Peek Policy

Do you happen to know, based on the dealer not peeking when a ten is up, whether the player loses the full amount bet or just the original bet to a dealer natural? As I understand it, if the player would lose the original bet only, then it doesn't mathematically matter whether or not the dealer peeks.

Quote: Mission146

...As I understand it, if the player would lose the original bet only, then it doesn't mathematically matter whether or not the dealer peeks...

Off topic - it makes a minute difference if the dealer has peeked as you know that card isn't an Ace. As an extreme in Single Deck case, if the dealer doesn't peek you would only know (say 6,5 vs 10) there are 4xA, 4x2, ...3x5, 3x6, ... 15x10 left. However if they have peeked your chances of getting an Ace are slightly higher (as they can't have one) and the other cards slightly lower (as there's a chance, about 3,4 or 15 in 45 the dealer has one). In practice I doubt it makes much difference, but if you're looking at finite decks it's something to be considered to get an accurate EV calculation. (I once spent ages trying to find why my figures were different and this was the reason!)

Quote: Mission146

RE: Peek Policy

Do you happen to know, based on the dealer not peeking when a ten is up, whether the player loses the full amount bet or just the original bet to a dealer natural? As I understand it, if the player would lose the original bet only, then it doesn't mathematically matter whether or not the dealer peeks.
link to original post

The player would lose the full amount bet.

I agree if he loses the original bet only, then it's mathematically the same as peeking.

Quote: charliepatrick

Quote: Mission146

...As I understand it, if the player would lose the original bet only, then it doesn't mathematically matter whether or not the dealer peeks...

Off topic - it makes a minute difference if the dealer has peeked as you know that card isn't an Ace. As an extreme in Single Deck case, if the dealer doesn't peek you would only know (say 6,5 vs 10) there are 4xA, 4x2, ...3x5, 3x6, ... 15x10 left. However if they have peeked your chances of getting an Ace are slightly higher (as they can't have one) and the other cards slightly lower (as there's a chance, about 3,4 or 15 in 45 the dealer has one). In practice I doubt it makes much difference, but if you're looking at finite decks it's something to be considered to get an accurate EV calculation. (I once spent ages trying to find why my figures were different and this was the reason!)
link to original post

Deck composition---good point, thanks!

Okay, I've spent the good part of the week on this game. That said, please see my analysis of Lightning Blackjack. Warning, my analysis is based on conventional basic strategy, which is not appropriate for this game. If you do play basic strategy, expect to lose 17.63% of your original bet, on average.

I welcome all comments.

When you only win half a unit on a BJ and 1 unit on a DD/Split after losing the Lightning Fee, is 17.63% even accurate? Oh yeah, you might hit a big win on the next hand with the multiplier, but even that average is under 3X. I'd be expecting the HA to be around 117%, not 17%. Winning your Lightning Fee back would be a whole 'nother calculation. But I would subtract 1 unit from the win side, or add another unit to the loss side of the 3rd chart to account for a Lightning Fee that is lost on a 0X multiplier.

Quote: Wizard

Okay, I've spent the good part of the week on this game. That said, please see my analysis of Lightning Blackjack. Warning, my analysis is based on conventional basic strategy, which is not appropriate for this game. If you do play basic strategy, expect to lose 17.63% of your original bet, on average.

I welcome all comments.
link to original post

Great page! The game is an even bigger disaster than I would have guessed re: not making decisions that deviate from conventional strategy.

Quote: Mission146

Great page! The game is an even bigger disaster than I would have guessed re: not making decisions that deviate from conventional strategy.
link to original post

Thank you.

There are a lot of ingredients that go into a successful casino game. Lightning Blackjack has most of them:

1. It's based on a familiar game.
2. The rules are not that complicated. They did a bad job of explaining them, but I think once you start playing, you catch on quickly.
3. The volatility is high, which most players like.
4. The speed (under normal playing conditions) is fast. Granted the live dealer/infinite player version is slow, but that can't be helped.

Where it fails is the strategy is not intuitive. The recreational blackjack player, using basic strategy, will get killed. Even Neil (from the video) said to not let the multipliers change your strategy.

I'm trying to make contact with Evolution to publish whatever math they have on the game. I'm not sure I can justify two weeks on the clock to develop one myself.

Quote: Wizard

Okay, I've spent the good part of the week on this game. That said, please see my analysis of Lightning Blackjack. Warning, my analysis is based on conventional basic strategy, which is not appropriate for this game. If you do play basic strategy, expect to lose 17.63% of your original bet, on average.

I welcome all comments.
link to original post

Based on your defined game rules and average multiplier values, as well as conventional basic strategy, my 1 billion trials simulation results show that the house advantage is 18.09%. A little bit different from yours, I don't know where I went wrong.

The current hand strategy largely depends on (current hand EV1 + next hand EV2), multiplier has a great influence on the basic strategy, and the correct basic strategy requires more accurate multiplier values.

Another question : Suppose you split, lose one hand and win the other. Is your multiplier still active in the next round ?

Quote: ssho88

Based on your defined game rules and average multiplier values, as well as conventional basic strategy, my 1 billion trials simulation results show that the house advantage is 18.09%. A little bit different from yours, I don't know where I went wrong.

I'm actually happy we are that close. This is a difficult game to simulate as there are lots of different game states. It is possible the error is on my end too.

Quote:

The current hand strategy largely depends on (current hand EV1 + next hand EV2), multiplier has a great influence on the basic strategy, and the correct basic strategy requires more accurate multiplier values.

I agree.

Quote:

Another question : Suppose you split, lose one hand and win the other. Is your multiplier still active in the next round ?
link to original post

I interpret the answer to that question as yes. You need just one win to earn a multiplier. Somebody correct me if I'm wrong.

Quote: Wizard

Quote: ssho88

Based on your defined game rules and average multiplier values, as well as conventional basic strategy, my 1 billion trials simulation results show that the house advantage is 18.09%. A little bit different from yours, I don't know where I went wrong.

I'm actually happy we are that close. This is a difficult game to simulate as there are lots of different game states. It is possible the error is on my end too.

link to original post

Woah!!!!
Are you guys saying the house edge is of the order of 18%?
My casino has this game and the help screen says the optimum theoretical return to player is 99.56%

How do we reconcile that?

Quote: OnceDear

Are you guys saying the house edge is of the order of 18%?
My casino has this game and the help screen says the optimum theoretical return to player is 99.56%

How do we reconcile that?
link to original post

The 99.56% return is based on optimal strategy, which nobody here has calculated yet. The 18% house edge is based on regular blackjack strategy. The takeaway should be to not play unless you know the mystery strategy.

Quote: Mission146

RE: Peek Policy

Do you happen to know, based on the dealer not peeking when a ten is up, whether the player loses the full amount bet or just the original bet to a dealer natural? As I understand it, if the player would lose the original bet only, then it doesn't mathematically matter whether or not the dealer peeks.
link to original post

Wouldn't it make a strategy difference? I.e. Peek on ten, you double an ace against 10, knowing he doesn't have blackjack. No peek, you would hit rather than double an ace against ten?

Wouldn't it be better to tell your readers to avoid this game entirely? A game that looks like BJ but has a house edge like the Big Six seems like a dream come true for the casino. Even our members who constantly defy the laws of math may struggle with such a game.
At what House edge do you advise folks to run away? Especially when the game itself is stating the house edge with perfect play is under 1%?

Quote: billryan

Wouldn't it be better to tell your readers to avoid this game entirely? A game that looks like BJ but has a house edge like the Big Six seems like a dream come true for the casino. Even our members who constantly defy the laws of math may struggle with such a game.
At what House edge do you advise folks to run away? Especially when the game itself is stating the house edge with perfect play is under 1%?
link to original post

If that was the case wouldnt you just advise to not play any negative EV game? If a player chooses to play a negative EV game then it is on the player to determine at what level would they accept. Many people are happy and get entertainment value out of play 20% hold slot machines. Obviously it is not for all of us.

Quote: billryan

Wouldn't it be better to tell your readers to avoid this game entirely? A game that looks like BJ but has a house edge like the Big Six seems like a dream come true for the casino. Even our members who constantly defy the laws of math may struggle with such a game.
At what House edge do you advise folks to run away? Especially when the game itself is stating the house edge with perfect play is under 1%?
link to original post

I told my readers the house edge is 18%. I'm not going to insult their intelligence by simply saying "don't play." They should be able to make that conclusion themselves.

I try to avoid shoving advice down my readers' throats. I lead them to water and let them decide to drink it or not.

Quote: DRich

Quote: billryan

Wouldn't it be better to tell your readers to avoid this game entirely? A game that looks like BJ but has a house edge like the Big Six seems like a dream come true for the casino. Even our members who constantly defy the laws of math may struggle with such a game.
At what House edge do you advise folks to run away? Especially when the game itself is stating the house edge with perfect play is under 1%?
link to original post

If that was the case wouldnt you just advise to not play any negative EV game? If a player chooses to play a negative EV game then it is on the player to determine at what level would they accept. Many people are happy and get entertainment value out of play 20% hold slot machines. Obviously it is not for all of us.
link to original post

I would think there is a point where it is better to advise people to avoid the game. I don't see anyone trying to work out a basic strategy for Pick Six because unless you find a person spinning by rote, no " smart" play can overcome the house edge.
I'd hope that a forum based on real math would absolutely advise its readers of the dangers of playing slots.
With casinos offering dozens of versions of BJ, this game seems based on appealing to people's greed and desire for bigger possible payouts. When I first read the rules a week or so ago, it seemed like a game designed to entrap suckers. The math seems to prove that.