Dividing a piece of land into equal parts

There is a piece of land that is triangular shaped.
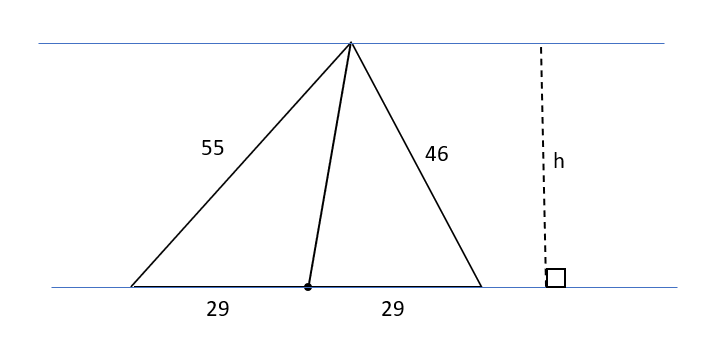
It is 58 meters by 55 meters by 46 meters.
The 55 meter side is frontage and has to be split at the middle point so at 29 meters.
How would the land be divided to make each piece the same area? I believe it leaves a triangle shape on one side and on the other side a 4 sided piece.
I知 stuck on this. Thanks anyone

Quote: Hunterhill

There is a piece of land that is triangular shaped.
The 55 meter side is frontage and has to be split at the middle point so at 29 meters.
link to original post

Ok, which side is split, the 55 or the 58? Also, any right angles in the original parcel? Also also, I assume you only get to use one straight line to divide the parcel?

Quote: Hunterhill

There is a piece of land that is triangular shaped.
It is 58 meters by 55 meters by 46 meters.
The 55 meter side is frontage and has to be split at the middle point so at 29 meters.
How would the land be divided to make each piece the same area? I believe it leaves a triangle shape on one side and on the other side a 4 sided piece.
I知 stuck on this. Thanks anyone
link to original post

To bisect the area of a triangle, just cut along a line from any vertex to the midpoint of the opposite side.

The area of a triangle equals one-half its base times its height. You can see in the diagram that both smaller triangles have the same base length and the same height. Therefore, they are equal in area.

Quote: ChesterDog

Quote: Hunterhill

There is a piece of land that is triangular shaped.
It is 58 meters by 55 meters by 46 meters.
The 55 meter side is frontage and has to be split at the middle point so at 29 meters.
How would the land be divided to make each piece the same area? I believe it leaves a triangle shape on one side and on the other side a 4 sided piece.
I知 stuck on this. Thanks anyone
link to original post

To bisect the area of a triangle, just cut along a line from any vertex to the midpoint of the opposite side.

The area of a triangle equals one-half its base times its height. You can see in the diagram that both smaller triangles have the same base length and the same height. Therefore, they are equal in area.


link to original post

Thanks Chester, how do I find out the height of the triangle

Quote: Hunterhill

Quote: ChesterDog

Quote: Hunterhill

There is a piece of land that is triangular shaped.
It is 58 meters by 55 meters by 46 meters.
The 55 meter side is frontage and has to be split at the middle point so at 29 meters.
How would the land be divided to make each piece the same area? I believe it leaves a triangle shape on one side and on the other side a 4 sided piece.
I知 stuck on this. Thanks anyone
link to original post

To bisect the area of a triangle, just cut along a line from any vertex to the midpoint of the opposite side.

The area of a triangle equals one-half its base times its height. You can see in the diagram that both smaller triangles have the same base length and the same height. Therefore, they are equal in area.

...
link to original post

Thanks Chester, how do I find out the height of the triangle
link to original post

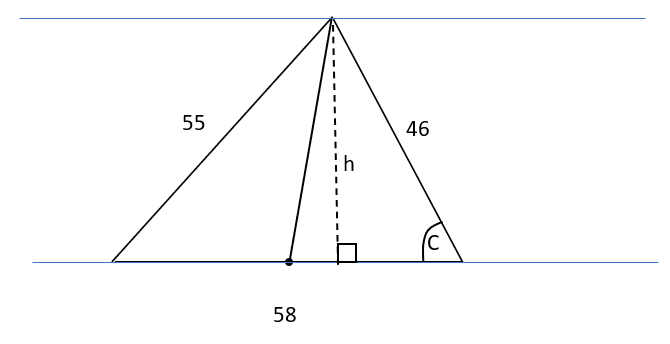
In this diagram, the height h equals 46 sin C.

To find C,we apply the "Law of Cosines," which is c² = a² + b² - 2ab cos C.

Rearrange this to: cos C = (a² + b² - c²) / (2ab)

Let a = 46, b = 58, and c = 55, then cos C is about 0.46008. And sin C equals the square root of 1 - cos²C, which is about 0.88788.

So, the height is about 46(0.88788) = 40.8423.

Thanks Chester. I found something called Herron痴 formula online which I think is basically what you did.
Greatly appreciated.

Quote: Hunterhill

There is a piece of land that is triangular shaped.
It is 58 meters by 55 meters by 46 meters.
The 55 meter side is frontage and has to be split at the middle point so at 29 meters.
How would the land be divided to make each piece the same area? I believe it leaves a triangle shape on one side and on the other side a 4 sided piece.
I知 stuck on this. Thanks anyone
link to original post

I think there is a typo? Did you mean to say the 58 meter side is frontage, not the 55 meter side? Splitting 55 meters would be 27.5, not 29.

Quote: ChesterDog

Quote: Hunterhill

Quote: ChesterDog

To bisect the area of a triangle, just cut along a line from any vertex to the midpoint of the opposite side.

The area of a triangle equals one-half its base times its height. You can see in the diagram that both smaller triangles have the same base length and the same height. Therefore, they are equal in area.

...
link to original post

Thanks Chester, how do I find out the height of the triangle
link to original post

In this diagram, the height h equals 46 sin C.

To find C,we apply the "Law of Cosines," which is c² = a² + b² - 2ab cos C.

Rearrange this to: cos C = (a² + b² - c²) / (2ab)

Let a = 46, b = 58, and c = 55, then cos C is about 0.46008. And sin C equals the square root of 1 - cos²C, which is about 0.88788.

So, the height is about 46(0.88788) = 40.8423.


link to original post

Fact is that you don't need to know the height. the two triangles formed reach the same peak, so have same height. They have same base width. Area=1/2 x base x height. So same area. All you needed to do was work out the mid point in the frontage.

Quote: SOOPOO

Quote: Hunterhill

There is a piece of land that is triangular shaped.
It is 58 meters by 55 meters by 46 meters.
The 55 meter side is frontage and has to be split at the middle point so at 29 meters.
How would the land be divided to make each piece the same area? I believe it leaves a triangle shape on one side and on the other side a 4 sided piece.
I知 stuck on this. Thanks anyone
link to original post

I think there is a typo? Did you mean to say the 58 meter side is frontage, not the 55 meter side? Splitting 55 meters would be 27.5, not 29.
link to original post

Yes that was a typo I meant the frontage was 58.

Quote: OnceDear

There are (at least) two other ways to calculate h.

First, let x be the distance from the left end of the 58-side to where the altitude intersects it; the distance from the right end is 58-x.
Solve for x using the Pythagorean Theorem twice:
h^2 = 55^2 - x^2 = 46^2 - (58 - x)^2
55^2 - x^2 = 46^2 - 58^2 + 116 x - x^2
55^2 - 46^2 + 58^2 = 116 x
x = 4273 / 116
h = sqrt(55^2 - (4273 / 116)^2) = 40.8423

Second, one formula for the area of a triangle with side lengths A, B, C, is sqrt(S (S-A) (S-B) (S-C)), where S = (A + B + C) / 2.
In this case, S = 159/2, so Area = sqrt(159/2 * 49/2 * 67/2 * 43/2) = 7 sqrt(458,079) / 4
Area = 1/2 * 58 * h = 29 h, so h = Area / 29 = 40.8423