Random and more random

Is there such a thing as more random? I understand that regular craps tables, mini crap tables, and bubble craps games are all producing random outcomes, but is one more random than the other? Do all RNG’s produce the same degree of randomness I.e.are Excell RNG functions as random as RNG’s used by casino games? Or is a random number a random number no matter how it’s produced ? Just wondering..

Many things advertised as random are not actually random.

I usually fall deep into superstition with dice, as in the dice are with me or against me no matter what I do. That's not randomness anymore, it's a curse at that point. Losing 10 odds bets in a row on the do side, then switching sides and losing 10 don't odds bets in row. That's how it rolls.

I can set the dice at the table and occasionally hit my 7-11 come-out wins, and that seems less random than normal. Or I can set for the point and hit that right away, and that seems like hitting a rifle shot in an arcade game. But sometimes, the earth just moves a little and my swing isn't right or the dice hit the wall a little different and everything falls apart. Think about how a pendulum rotates around as the earth rotates around. The good cycles don't last long and it's on to the next.

Both Excel and most slot machines use some sort of complex pseudo-random function, of which there are many. Most of these modern functions are so random that it's hard to measure any bias, but some functions are faster than others.

There are "tests" for randomness, but, by themselves, some work better than others.
There are 12 general tests mentioned in the second volume of Donald Knuth's The Art of Computer Programming; however, the first one is, "Count the number of times each result comes up, and see how close they get to being equal," which makes the "random" sequence 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, ... "truly" random.

Some methods work better if the range of numbers needed is limited. For example, if you want to simulate a dice roll or a roulette wheel spin, you can do what I did for a hardware project in college over 40 years ago; the aforementioned "1, 2, 3, 4, 1, 2, 3, 4, ..." method, but really fast (I ran it at 1,000,000 results per second), with the number chosen when someone pushes a button. This doesn't work as well with larger numbers, as there are some people who can time the button to 1/10,000 of a second; if the RNG is driving a slot machine with a selection rate of 1,000,000 per second, if you know when the jackpot number came up, you can reduce the probability of finding it again to 1 /100.

The "standard" method is this: to generate a random integer from 0 to N - 1 for some N, find two numbers M and A, let R be any of the integers in the range, then generate the next number = (M R + A) mod N. If M and A meet certain conditions (A and N do not share any factors > 1; M - 1 is a multiple of every prime factor of N; N is not a multiple of 4 and/or M - 1 is a multiple of 4), then any set of N consecutive numbers will have every number from 0 to N - 1 exactly once. Some of these are "more random" than others; there is a specific test for this. One set of M, A, and N that failed miserably was IBM's random number function that it included in its large computers.

I once saw a method for an old-school IBM 1130 "big-iron" computer that generated random numbers by "reading" them from the line printer.

I only got three Royal Flushes in the last several years, but a co-player of mine got six in one year. Disturbing that guy didn't even know basic strategy for ultimate Texas Hold’em. This is the randomness of casino gambling.

If we look at general possibilities, there are 36 outcomes for 2 dice of different color. 1 Million outcomes per second of a randomized list of outcomes 'should' have a very slight difference to resetting the dice to original order repeatedly.

One of they early 'home-user' randomizers was to to randomize a list of items 3 or 7 times then randomly select item(s). You might say shuffle a deck of cards 3 or 7 times (chosen randomly), then select random cards from the deck. *** Of course this is NOT the way card games are dealt, after the 3 or 7 shuffle, cards are dealt off-the-top. *** It would be interesting to know if this method is used in poker websites... they might be illegal if NOT dealt consecutively off-the-top after shuffle.

Quote: technics

Is there such a thing as more random? I understand that regular craps tables, mini crap tables, and bubble craps games are all producing random outcomes, but is one more random than the other? Do all RNG’s produce the same degree of randomness I.e.are Excell RNG functions as random as RNG’s used by casino games? Or is a random number a random number no matter how it’s produced ? Just wondering..
link to original post

In an esoteric sense I would say some RNG's are more random than others, but honestly none of them ar random they are just the output of a formula. If you run an RNG multiple times with the same inputs you will always get the same outputs.

So the dinosaurs invented a computer in the 1970s called "Apple II" and it had something called "Applesoft Basic" in ROM (like a chip with stuffs on it). This ROM had a function called RND() that would return a random number between 0 and 1.
Now, we would think that if we wrote this

and ran it forever, then we would eventually see the screen fill up with dots. After nH_n iterations, we should have the board filled on average, right? It is a "coupon collector" problem.
But if we did run it forever, we would see something like this for all times after 7 minutes or so:

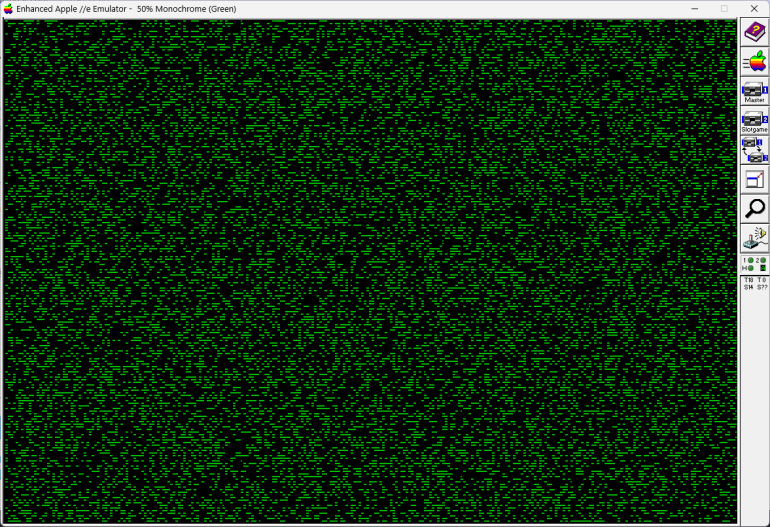
Turns out that the period, math word for how long the stream is, is really short. It starts repeating the sequence after a short time. If print out the RNG values for our thing, we would see a sequence of 37,758 numbers that would just keep repeating. It is a "bad" RNG. It is only random for a very short time, then it is very predictable.
"Good" RNGs have much larger streams. PCG-random is 2^64, which would take 58.5 million years to exhaust if we go through 10,000 numbers per second. Mersenne twister is 2^19000-whatever minus 1.

I just read an online article, Random Seeds and Reproducibility. There are two aspects of each RNG, seed and reproducibility. The RNG I’m using has several millions of seed numbers for me to choose one from, but I haven’t understood these things. For each seed, the RNG produces a fixed number sequence, which is pseudo-random.

Quote: aceside

I just read an online article, Random Seeds and Reproducibility. There are two aspects of each RNG, seed and reproducibility. The RNG I’m using has several millions of seed numbers for me to choose one from, but I haven’t understood these things. For each seed, the RNG produces a fixed number sequence, which is pseudo-random.
link to original post

One of the ways to use that is to use "real" random entropy to select a seeded sequence. One of the common ways to collect random entropy is to observe timing data from physically wiggling a mouse.

(If you need a valid entropy pool, don't use a "jiggler" to keep Teams from sleeping. Duh.)

Quote: itsmejeff

Turns out that the period, math word for how long the stream is, is really short. It starts repeating the sequence after a short time. If print out the RNG values for our thing, we would see a sequence of 37,758 numbers that would just keep repeating. It is a "bad" RNG. It is only random for a very short time, then it is very predictable.
"Good" RNGs have much larger streams. PCG-random is 2^64, which would take 58.5 million years to exhaust if we go through 10,000 numbers per second. Mersenne twister is 2^19000-whatever minus 1.
link to original post

The length of a period is not necessarily a sign of a "good" RNG. The "random" sequence 1, 2, 3, ..., 2^65,536 has a period of 2^65,536, but I would hardly call it "random."

You can generate a random sequence of period 2^N using the formula I mentioned above (if R is the most recent number, or the seed if you have not started yet, the next number is (R M + A) mod 2^N, if A is any odd number and M is any positive integer that is 1 more than a multiple of 4. If you want a period of 10^N, then A is any odd number that does not end in 5, and M is 1 more than a multiple of 20.

I would like to add that wind noise and radioactivity are natural sources of random generation. At my college back in the late 70's the computer center had a box with geiger tube attatched. This was for seed generation.

Quote: Danbury

I would like to add that wind noise and radioactivity are natural sources of random generation. At my college back in the late 70's the computer center had a box with geiger tube attatched. This was for seed generation.
link to original post

Wow, I am shocked it had a Geiger counter attached in the 1970's. Do you mind me asking which college?

Quote: Danbury

I would like to add that wind noise and radioactivity are natural sources of random generation. At my college back in the late 70's the computer center had a box with geiger tube attatched. This was for seed generation.
link to original post

What, you didn't just hang a microphone out the window and pick up street noise?