Feeling unlucky ...

I know enough about math and high variance to not take variance personally, but I still feel "unlucky." But maybe the math geeks in this forum can tell me what certain probabilities are.

MATH QUESTION: Assume the game has a 1.5% HE. For each "session," I like to risk 80 credits and will quit when a) I'm out of credits or b) I have 120 or more credits. Bet is 5 per hand. What is the probability that I have exactly 11 "sessions" in a row without ending a session under Scenario B?

STORY BEHIND THE MATH QUESTION: I work in Hughes Center and I like nice restaurants so a couple of times a week I'll bounce over to Secretion/Palazzo for a nice lunch. Most times, I'll toss in $20 at a 25c VP machine and play a session just for fun. I've been to 11 good and not-so-good restaurants but I have yet to have a single winning session.

[Wargames_computer_voice] The only winning move is not to play. [/Wargames_computer_voice]

Quote: MrWarmth

I know enough about math and high variance to not take variance personally, but I still feel "unlucky." But maybe the math geeks in this forum can tell me what certain probabilities are.

MATH QUESTION: Assume the game has a 1.5% HE. For each "session," I like to risk 80 credits and will quit when a) I'm out of credits or b) I have 120 or more credits. Bet is 5 per hand. What is the probability that I have exactly 11 "sessions" in a row without ending a session under Scenario B?

STORY BEHIND THE MATH QUESTION: I work in Hughes Center and I like nice restaurants so a couple of times a week I'll bounce over to Secretion/Palazzo for a nice lunch. Most times, I'll toss in $20 at a 25c VP machine and play a session just for fun. I've been to 11 good and not-so-good restaurants but I have yet to have a single winning session.

[Wargames_computer_voice] The only winning move is not to play. [/Wargames_computer_voice]

There is not enough information to answer your question. You mentioned variance in your preamble, and then failed to give information about it in your question.

Generally, the higher the variance, the more likely that you will have a winning session (note, however, that variance is not enough to answer your question -- we need the exact probability distribution. Assuming that it's normal would be a big mistake)

In particular, for video poker, you will lose most of your sessions because you are risking a very small amount of money ($20) for a chance to win a lot ($1000). Your claim that you will quit when you have $30 or more is extremely misleading because you will often quit with way, way, way more than $30.

The best way to answer this question would be through simulation (a normal approximation will be way off). What is the game and paytable?

Quote: AxiomOfChoice

There is not enough information to answer your question. You mentioned variance in your preamble, and then failed to give information about it in your question.

Generally, the higher the variance, the more likely that you will have a winning session (note, however, that variance is not enough to answer your question -- we need the exact probability distribution. Assuming that it's normal would be a big mistake)

In particular, for video poker, you will lose most of your sessions because you are risking a very small amount of money ($20) for a chance to win a lot ($1000). Your claim that you will quit when you have $30 or more is extremely misleading because you will often quit with way, way, way more than $30.

The best way to answer this question would be through simulation (a normal approximation will be way off). What is the game and paytable?

Well, OK, I'm not sure what was misleading about "quit with 120 or more credits," I don't play it down to exactly 120 every time, but if a paytable is needed, how about the 50/7/5 on https://wizardofodds.com/games/video-poker/tables/bonus-poker/. I see that's about a 2% HE but it's probably the paytable I see most there.

Quote: MrWarmth

Well, OK, I'm not sure what was misleading about "quit with 120 or more credits," I don't play it down to exactly 120 every time, but if a paytable is needed, how about the 50/7/5 on https://wizardofodds.com/games/video-poker/tables/bonus-poker/. I see that's about a 2% HE but it's probably the paytable I see most there.

The misleading part is that you have a small chance of quitting with over 4000 credits. This would not be true if you were playing a game like blackjack, for example.

Quote: AxiomOfChoice

The misleading part is that you have a small chance of quitting with over 4000 credits. This would not be true if you were playing a game like blackjack, for example.

4,000 > 120, so is 121. What does it matter so long as it's >120 and I stop? I'm not sure I ever mentioned BJ. I'm not trying to be argumentative, I just don't see how it matters esp. when BJ was never part of the question.

Quote: MrWarmth

4,000 > 120, so is 121. What does it matter so long as it's >120 and I stop? I'm not sure I ever mentioned BJ. I'm not trying to be argumentative, I just don't see how it matters esp. when BJ was never part of the question.

It matters because it means that you hit your win goal a lot less often. You need an awful lot of losses to make up for the monster wins! Remember that the mean result is a loss. So when you add up all your wins and losses you get a negative number. It takes many -80's to cancel out a +3960.

The same is true with the high-paying quads. It doesn't take as many to cancel each one out, but you hit a lot more of them.

Variance is kind of strange with this problem. If the variance is too low, you end up doing too much play before you either hit your win goal or go broke (remember that the more you pay, the lower your average result, since your average result is -2% of your average amount of action, so more play means a lower average result). On the other hand, if you get to very high variance by a few very rare high payouts, then you lose most of your sessions, which is the case here. To maximize the number of winning sessions, you want a paytable that closely approximates the "bold play" approach, where one big win will take you to your win goal, but not too much past it.

Anyway, for this particular paytable, it can be simulated and you will get your answer. Raise your probability of losing to the power of 11 and you have your answer.

Quote: AxiomOfChoice

It matters because it means that you hit your win goal a lot less often. You need an awful lot of losses to make up for the monster wins! Remember that the mean result is a loss. So when you add up all your wins and losses you get a negative number. It takes many -80's to cancel out a +3960.

The same is true with the high-paying quads. It doesn't take as many to cancel each one out, but you hit a lot more of them.

Variance is kind of strange with this problem. If the variance is too low, you end up doing too much play before you either hit your win goal or go broke (remember that the more you pay, the lower your average result, since your average result is -2% of your average amount of action, so more play means a lower average result). On the other hand, if you get to very high variance by a few very rare high payouts, then you lose most of your sessions, which is the case here. To maximize the number of winning sessions, you want a paytable that closely approximates the "bold play" approach, where one big win will take you to your win goal, but not too much past it.

Anyway, for this particular paytable, it can be simulated and you will get your answer. Raise your probability of losing to the power of 11 and you have your answer.

Oh, I think I see the disconnect. I'm not looking at the overall win. I'm just looking at the session-by-session win. In other words, as far as it concerns this question, there's no difference in whether the 11 sessions, in aggregate, are positive or negative.

If I were to take it to 12, I would consider my "losing streak" broken if I cashed out at 120, even though, clearly, for the 12 sessions overall, I'd be down 840. While the "overall win" is not unimportant to the wallet, I'm not thinking of it here.

Does that help clarify? My bad for the ambiguity.

Quote: MrWarmth

Oh, I think I see the disconnect. I'm not looking at the overall win. I'm just looking at the session-by-session win. In other words, as far as it concerns this question, there's no difference in whether the 11 sessions, in aggregate, are positive or negative.

If I were to take it to 12, I would consider my "losing streak" broken if I cashed out at 120, even though, clearly, for the 12 sessions overall, I'd be down 840. While the "overall win" is not unimportant to the wallet, I'm not thinking of it here.

Does that help clarify? My bad for the ambiguity.

I completely understand what you are saying. But my point is, the fact that there are very large payouts which will push you far, far beyond your win goal means that you will have a disproportionate amount of losses.

The reason that I said that it was misleading originally was that, the way it was phrased, it seemed as if you were risking 80 to win 40, in which case you should win quite often. But this is not true -- you are risking 80 to win AT LEAST 40 -- possibly much, much, much more than 40 (100x as much, in fact). So, that will increase your loss rate significantly.

Without simulating it, I'm not going to be able to give you an exact answer. And I'm probably not going to simulate it. Maybe you can, or maybe someone else will.

Quote: AxiomOfChoice

I completely understand what you are saying. But my point is, the fact that there are very large payouts which will push you far, far beyond your win goal means that you will have a disproportionate amount of losses.

The reason that I said that it was misleading originally was that, the way it was phrased, it seemed as if you were risking 80 to win 40, in which case you should win quite often. But this is not true -- you are risking 80 to win AT LEAST 40 -- possibly much, much, much more than 40 (100x as much, in fact). So, that will increase your loss rate significantly.

Without simulating it, I'm not going to be able to give you an exact answer. And I'm probably not going to simulate it. Maybe you can, or maybe someone else will.

Hmm ... OK. I can't say I understand it, but OK. Wouldn't it just be the probability of (losing all 80, 5 at a time) ^11 since the "trials" are independent?

EDIT: No, I guess it wouldn't since I stop if >120. Oh well.

Quote: MrWarmth

Hmm ... OK. I can't say I understand it, but OK. Wouldn't it just be the probability of (losing all 80, 5 at a time) ^11 since the "trials" are independent?

Yes. But the probability of losing all 80 is not easy to figure out without a simulation. Because, you will not usually lose 16 hands in a row! There will often be ups and downs.

Maybe it can be brute-forced. There are only 24 different states, after all.

Quote: MrWarmth

I know enough about math and high variance to not take variance personally, but I still feel "unlucky." But maybe the math geeks in this forum can tell me what certain probabilities are.

MATH QUESTION: Assume the game has a 1.5% HE. For each "session," I like to risk 80 credits and will quit when a) I'm out of credits or b) I have 120 or more credits. Bet is 5 per hand. What is the probability that I have exactly 11 "sessions" in a row without ending a session under Scenario B?

I agree the knowledge of the house edge for what you want is meaningless in my opinion.
The pay table and probabilities are what one is after.

Now for 11 sessions in a row not to hit your win target, are you cherry picking this?
meaning you have only done this 11 times?

because the probability of 11 losing sessions in a row say over 20 sessions played
is higher than just the very next 11 sessions (f that is all you have played and I doubt that)

yes, this can be simulated for the
one session win goal probability

but there are programs free and paid (like Video Poker for Winners) that can calculate this for you quite easily and fast convolving the probability distribution
(I think I said that right)

I get (using 2 different programs) for 7/5 BP
58.2% chance of ruin
41.8% chance of success

so for only 11 sessions played = 58.2%^11 = 0.002595092431930
about 1 in 385.34
not astronomical

some other values:
over 20 sessions that increases to
0.012357830160852
about 1 in 80.92

40 sessions
0.033822209298206
about 1 in 29.57

100 sessions
0.095451879958601
about 1 in 10.48

These values assume perfect play too
is that a possibility?
IF not than these probabilities are too low

Sally

forgot my photos



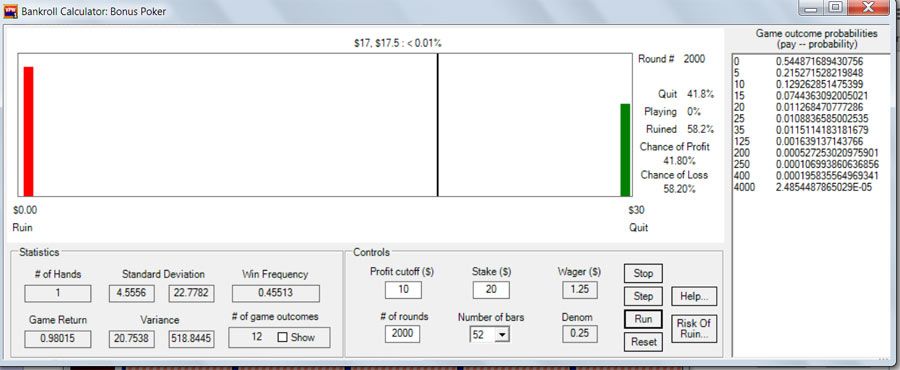
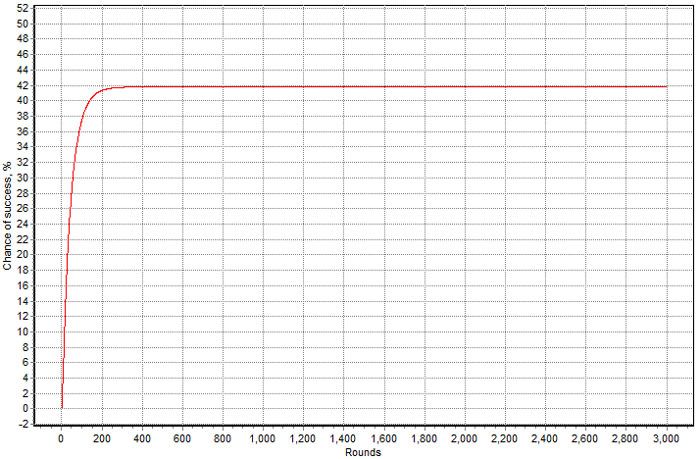
now if you only play 100 hands I show a 37.5% chance of success against a 44.3% chance of ruin
that leaves 18.2% still having credits left and not hitting your bankroll target

If the game played is 7/5 Bonus Poker, a simulation I just ran agrees with the previous post; a success rate of approximately 41.8%, therefore the odds of failure in your next 11 consecutive sessions would be about 1 in 385.

Thanks! I guess 1 in 385 to the bad is pretty "unlucky" as I have lost 11 straight sessions.

Sally: yes, I was cherry-picking with the 11 figure. 11 is the number of consecutive sessions where I've busted. That's where that number came from. I don't know what it is over the longer term but I can't imagine it would be significantly different than the 58/42 probability you've calculated.

Also, my play was probably not exactly perfect as I don't have Wizard's table memorized, but it's probably only a few tenths off. I wouldn't guess this would turn 1/385 into anything worse than 1/(385+25) ... and that figure is pulled out from my ass. I know every little bit helps ...

Hopefully a fun exercise for you math types ... although I'm not sure how I feel about my "bad luck" being quantified, but I did ask ... ;)

Thanks again!

Quote: MrWarmth

Hopefully a fun exercise for you math types ... although I'm not sure how I feel about my "bad luck" being quantified, but I did ask ... ;)

Thanks again!

when a program can do the math in a second, I could call that fun.
I also like to set up a transition matrix in Excel (some at 2002x2002 - other programs can do this too)
and get a bunch of data all at once.
It takes a few minutes and to me that is fun.
and I now always have that info.
(For different VP games, I can just swap out the new pay table too)

Here is a table with at least a 120 credit target, Ruin (0) and # starting Bankroll credits
You have about a coin toss chance of hitting 120 credits by starting with 90 credits instead of 80
(actually you are now a slight favorite to hit your target)

note that starting with 119 credits and trying to get at least 120
is not at all a sure thing.
I think most would think it would be
(this still considers a 5 coin bet. Not as much fun hitting a 4oak or higher with 1 credit bet.
I do see many seniors playing this way, BTW. 1 credit and hit Deal)
Sally

120+	0	bankroll (credits)
0.004049122	0.995950878	1
0.008314712	0.991685288	2
0.01258479	0.98741521	3
0.017399308	0.982600692	4
0.021225076	0.978774924	5
0.025188255	0.974811745	6
0.029363308	0.970636692	7
0.033542753	0.966457247	8
0.038255083	0.961744917	9
0.042530735	0.957469265	10
0.046407644	0.953592356	11
0.050491816	0.949508184	12
0.054580285	0.945419715	13
0.059190038	0.940809962	14
0.06398903	0.93601097	15
0.067779053	0.932220947	16
0.071771692	0.928228308	17
0.075768532	0.924231468	18
0.080274974	0.919725026	19
0.085682291	0.914317709	20
0.089384475	0.910615525	21
0.09328458	0.90671542	22
0.097188788	0.902811212	23
0.101590787	0.898409213	24
0.107704652	0.892295348	25
0.111317665	0.888682335	26
0.115123831	0.884876169	27
0.118934002	0.881065998	28
0.123229974	0.876770026	29
0.130164145	0.869835855	30
0.133686216	0.866313784	31
0.13739658	0.86260342	32
0.141110846	0.858889154	33
0.145298687	0.854701313	34
0.153184174	0.846815826	35
0.156613035	0.843386965	36
0.160225204	0.839774796	37
0.163841174	0.836158826	38
0.167918184	0.832081816	39
0.176907354	0.823092646	40
0.180240157	0.819759843	41
0.183751133	0.816248867	42
0.187265802	0.812734198	43
0.191228597	0.808771403	44
0.201497099	0.798502901	45
0.204730334	0.795269666	46
0.20813642	0.79186358	47
0.21154609	0.78845391	48
0.215390497	0.784609503	49
0.227143927	0.772856073	50
0.230273315	0.769726685	51
0.233570003	0.766429997	52
0.236870159	0.763129841	53
0.240591088	0.759408912	54
0.254062888	0.745937112	55
0.257083278	0.742916722	56
0.26026514	0.73973486	57
0.26345035	0.73654965	58
0.267041678	0.732958322	59
0.282514772	0.717485228	60
0.285419957	0.714580043	61
0.288480455	0.711519545	62
0.291544173	0.708455827	63
0.294998519	0.705001481	64
0.312750664	0.687249336	65
0.31553342	0.68446658	66
0.318464945	0.681535055	67
0.321399553	0.678600447	68
0.324708327	0.675291673	69
0.345127248	0.654872752	70
0.347778907	0.652221093	71
0.350572326	0.649427674	72
0.353368684	0.646631316	73
0.356521581	0.643478419	74
0.380011458	0.619988542	75
0.382521867	0.617478133	76
0.385166484	0.614833516	77
0.387813884	0.612186116	78
0.39079883	0.60920117	79
0.417971876	0.582028124	80
0.420328579	0.579671422	81
0.422811272	0.577188728	82
0.425296578	0.574703422	83
0.428098763	0.571901237	84
0.459402211	0.540597789	85
0.461591157	0.538408843	86
0.463897126	0.536102874	87
0.46620552	0.53379448	88
0.468808238	0.531191762	89
0.505878936	0.494121065	90
0.507879692	0.492120308	91
0.50998741	0.49001259	92
0.512097345	0.487902655	93
0.5144763	0.4855237	94
0.554867522	0.445132478	95
0.556669917	0.443330083	96
0.55856867	0.44143133	97
0.56046942	0.43953058	98
0.562612519	0.437387481	99
0.6091255	0.3908745	100
0.610708198	0.389291802	101
0.612375509	0.387624491	102
0.614044573	0.385955427	103
0.615926446	0.384073554	104
0.668706311	0.331293689	105
0.670047759	0.329952241	106
0.671460923	0.328539077	107
0.672875572	0.327124428	108
0.674470592	0.325529408	109
0.740260574	0.259739426	110
0.741312291	0.25868771	111
0.742420233	0.257579767	112
0.74352934	0.25647066	113
0.74477986	0.25522014	114
0.819651427	0.180348573	115
0.820381681	0.179618319	116
0.821150974	0.178849026	117
0.821921076	0.178078924	118
0.822789368	0.177210632	119

And make it 12!

I know that the probability of ruin for the 12th trial after 11 consecutive ruins is 58.2%, but the probability of 12 consecutive ruins is 662:1.

But my luck will change soon ... I can **FEEL** it!!!!

OK, despite being in another run of bad variance, this time 7 busts in a row, or 0.582^7 = 1 in 44 ...

Recalling I like to bet 80 credits 5 at a time on Bonus Poker, or 16 bet "bankroll," I had 18 plays; that is, 16 no-result and 2 get-your-bet-back result, so I went to https://wizardofodds.com/games/video-poker/tables/bonus-poker/ (50/7/5) to see how unlucky that was.

Is this calculation right?

0.544872^16 x 0.215272^2 = 1 in ~358,000 chance of this happening.

Quote: MrWarmth

0.544872^16 x 0.215272^2 = 1 in ~358,000 chance of this happening.

you are off by a factor of 153
I get
1 in 2336.8 for exactly the 16,2

but it is actually lower (1 in 1744.3 - check my math) if we consider 17,1 and 18,0 (shutout)
I think you will be able to crunch those numbers too

you really need to consider the number of combinations of outcomes
Being that you have 3 outcomes (or more) the
multinomial distribution is now your friend
http://easycalculation.com/statistics/multinomial-distribution.php
http://stattrek.com/probability-distributions/multinomial.aspx?tutorial=stat

Google: (18! / (16! * 2! * 0!)) * 0.544872^16 * 0.215272^2 * 0.239856^0
should = 0.000427936

where 0.239856^0 = 1

Excel =(FACT(18) / (FACT(16) * FACT(2) * FACT(0))) * (0.544872^16 * 0.215272^2 * 0.239856^0)

So I better not even mention I hit my 5th and 6th Royals last week in maybe 5 hours of total play
and I am only 24 (lifetime hands = about 30k and most at CA Indian Casinos, they must really like me)

nothing like skill and luck
Sally

Thanks, mustangsally, for the math and clarification!

Nah, I never begrudge others their wins, I'm happy when people win. Just buy a drink for the guys next to you some time!

I am newbie to poker and getting training from some poker training software. You can use Ace Poker Drills to learn about the basic and advance math of poker.

Quote: mustangsally

....

but there are programs free and paid (like Video Poker for Winners) that can calculate this for you quite easily and fast convolving the probability distribution
(I think I said that right)

Yes, this is exactly right, at least for Video Poker for Winners. That code takes the exact probability distribution for the player's revenue from one hand, and convolves the distribution to get the exact distribution for the total revenue from n hands. Basically it does
" (Rev. from n hands) convolved with (Rev. from 1 hand) = (Rev. from n+1 hands) " in a loop.

It then shows the result as a histogram, which might require some binning of probabilities in order to make a pretty picture.

I usually play $5.00 at a time in quarter machines, so I can change machines if I don't get any winners. I have noticed that machines will run in spurts of wins and losses. Sometimes I will have 5 losses in a row and then 5 or 6 wins in a row. You may be on machines that are in down modes.