"Trip bankroll" requirements

Suppose I'm considering playing a promotion. I will play 9/6 JoB at 5 coins/hand. Say I am capable of playing perfectly. Ignore freeplay and comps; I will not be cashing anything in until after the promotion.

Suppose I plan to play about 20,000 hands (about half a royal cycle). How much cash would you think I should take with me, and be comfortable with possibly losing? I was thinking 4000 coins (800 bets -- one royal payoff). But, then I was thinking, in order to go broke over 20,000 hands, I would have to lose at a rate of 4%. My expected loss between royals is about 2.5% (since 2% of my return comes from Royals). 4% seems dangerously close to that 2.5% number.

Thoughts? From people who have done something like this before, how much money is appropriate?

As for figuring it out myself: I am reluctant to assume that my results would be normally distributed; I'm not sure that this is enough hands, considering the possibility of a single large payout. I'd almost expect the results to be bimodally distributed -- results where I hit a royal and results where I don't. I suppose I could work under the assumption that I won't hit a RF, and use the standard deviation and EV under those assumptions. I could also just run some simulations and see what the graph looks like. Again, I'd like to get the opinions of experienced people before I do that, though.

It looks like it will be rather multimodal (similar to how you hypotheized). The figure below show 100 replications of 20,000 hands. On the y axis is you total five coin bets result (multiply by 5 to get total coin results). The x axis is the number of royals hit.



This data took a few seconds to make. I will begin a larger run soon to get more replications so that the patterns are more discernable. I also have tracked the maximum amount down in a realization and will post that info.

Here is 1000 replications in a histogram. We can see 3 lumps already formed and a fourth one probably about to start.



This one helps show the multi-modality better.


I'm going to let my laptop do a huge run overnight and post the results (including safe bankroll requirements) when I get up. Below is my code:

The return of the game - a royal - straight flush * $/hand - $/hand * total hands.

Then multiply by however you think you will run. If no 4oak per cycle you might feel a pinch

Quote: djatc

The return of the game - a royal - straight flush * $/hand - $/hand * total hands.

Then multiply by however you think you will run. If no 4oak per cycle you might feel a pinch

I think this is a good back of the envelope approach, but I wouldn't drop the straight flushes for in AoC's example

Quote: AxiomOfChoice

Suppose I plan to play about 20,000 hands (about half a royal cycle).

Quote: endermike

Here is 1000 replications in a histogram. We can see 3 lumps already formed and a fourth one probably about to start.



This one helps show the multi-modality better.


I'm going to let my laptop do a huge run overnight and post the results (including safe bankroll requirements) when I get up. Below is my code:

function out = AoCVP(hands, reps)

data = [0, 0.54543467;
    1, 0.76001969;
    2, 0.88929859;
    3, 0.96374729;
    4, 0.97497666;
    6, 0.98599117;
    9, 0.99750338;
    25, 0.99986593;
    50, 0.99997524;
    800, 1.00000001];

results = zeros(reps, 3);

for r = 1:reps
    current = 0;
    royals = 0;
    worst = 0;
    for h = 1:hands
        res = rand(1);
        ind = find(res<data(:,2), 1, 'first');
        current = current+data(ind,1)-1;
        if ind == 10
            royals = royals+1;
        end
        worst = min(worst,current);
    end
    results(r,:) = [current, royals, worst];
end

out = results;

Wow, Mike, thanks! That is way above and beyond what I was expecting.

So, it looks like 800 bets is probably enough, and 1000 bets down would be pretty bad luck, and 1200 bets is almost certainly enough.

Geez, losing 1 and a half royals in half a cycle sounds horrible. That is a big hole...

Quote: AxiomOfChoice

Suppose I'm considering playing a promotion. I will play 9/6 JoB at 5 coins/hand. Say I am capable of playing perfectly. Ignore freeplay and comps; I will not be cashing anything in until after the promotion.

Suppose I plan to play about 20,000 hands (about half a royal cycle). How much cash would you think I should take with me, and be comfortable with possibly losing? I was thinking 4000 coins (800 bets -- one royal payoff).

I think you should ask the casino you are planning to play at for $10,000 in casino credit.
No worry about busting out.

Yes, Please try and use ev and sd to produce the distribution for 20k hands also.
no one else really seems interested at all in this. (most do not like things that are not normal)

here are a few runs of 100k each with rolls of 4,5 and 6k
bust rates from 11% on down.
Just do not think you will end up around the ev for one 20k session.
look up and to the left to see how much you can lose in a very long 20k session.




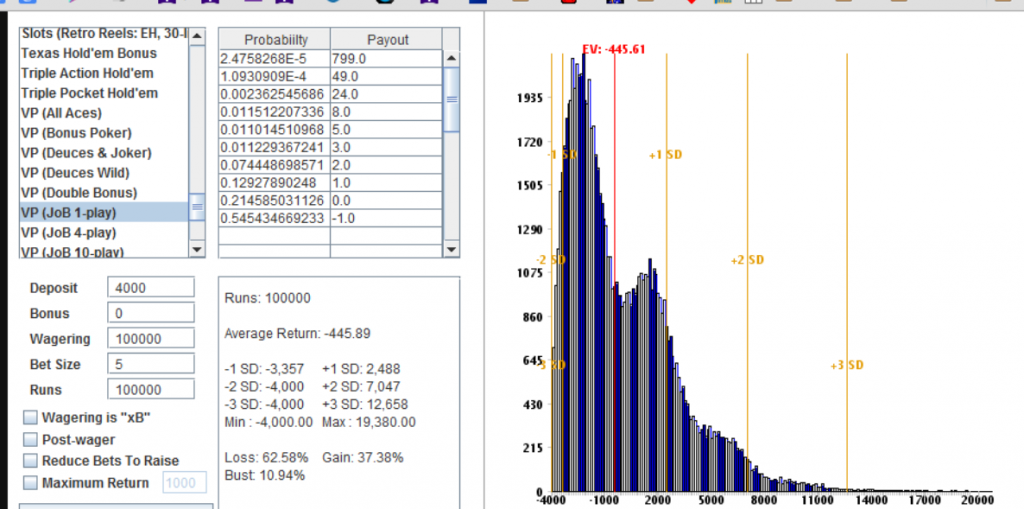
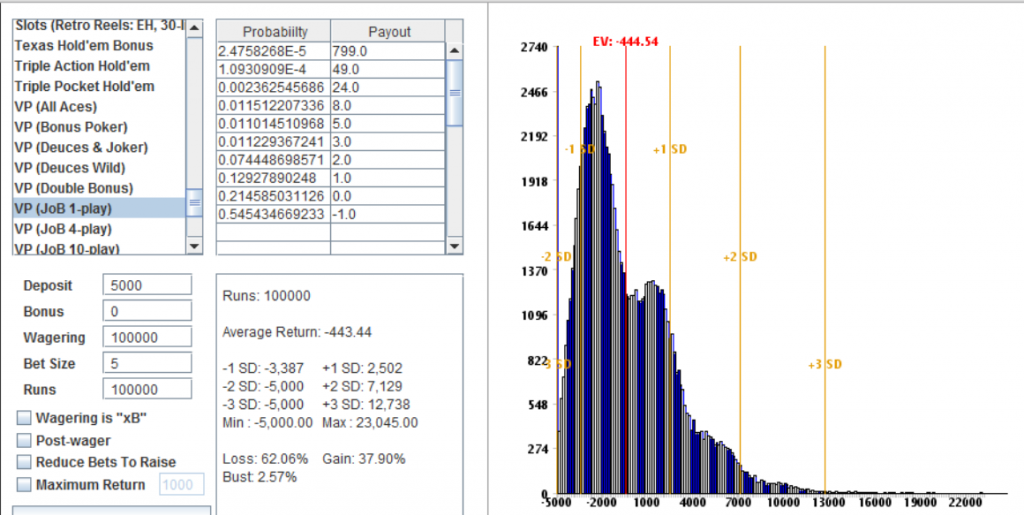
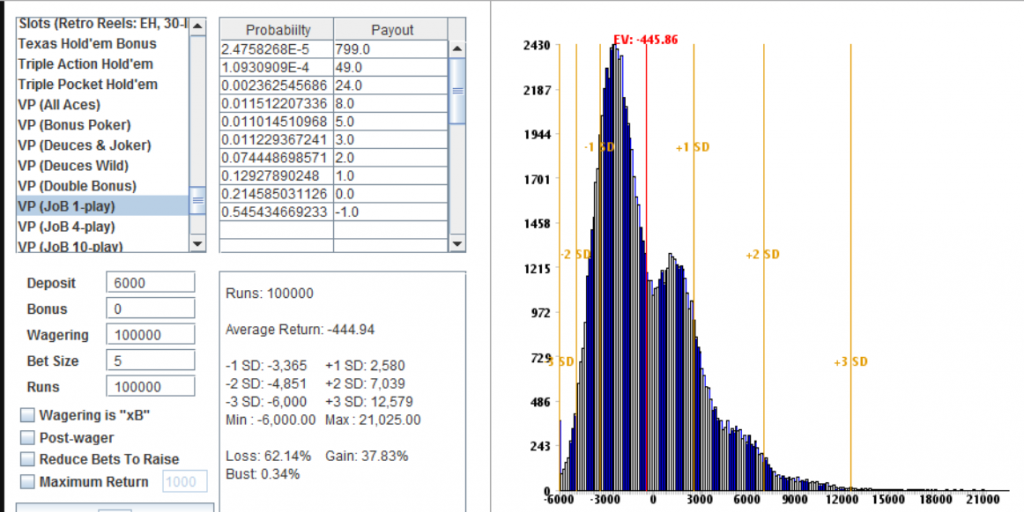
a different look
the 799unit bankroll cumulative graph


Sally

Quote: mustangsally

I think you should ask the casino you are planning to play at for $10,000 in casino credit.
No worry about busting out.

Wait, I haven't told you what level I'm playing at. Are you assuming that 1 coin = $1? (It doesn't, but I can multiply)

Quote:

Just do not think you will end up around the ev for one 20k session.

Oh, I don't. That's why I asked this. I'm well aware that I will probably be either way up or way down, depending on whether I hit a royal or not -- and I am less than 50% to hit a royal in half a cycle. That's basically why I want to see these numbers.

The other problem is that once the promotion is over, I have no desire to keep playing this (at least until the next promotion pops up) so I can't count on "the long term" to bail me out.

Thanks for the data -- I appreciate it. It will take me a while to read it and figure out if I want to take this much risk or not.

Quote: AxiomOfChoice

Wait, I haven't told you what level I'm playing at. Are you assuming that 1 coin = $1? (It doesn't, but I can multiply)

I assumed units
I just threw out (in) $10k as a nice round number.

Quote: AxiomOfChoice

Oh, I don't. That's why I asked this. I'm well aware that I will probably be either way up or way down, depending on whether I hit a royal or not -- and I am less than 50% to hit a royal in half a cycle.

39.0530% about for 20k hands
I have now 4 Royals (all last year) to my credit in about that many hands, a little less I think
not at 9/6 JOB

so get 4 Royals (or more) and that should take away any worry of a risk of any kind of loss.

Sally

And here is the final thing you you need. These polots are based on 2,000,000 independent replications in Matlab using my previous code.

First here is the distribution of net outcomes:


Second the distribution of maximum amount down. THIS IS THE IMPORTANT GRAPH! This is the distribution of required bankrolls to make it to the end of 20,000 hands:


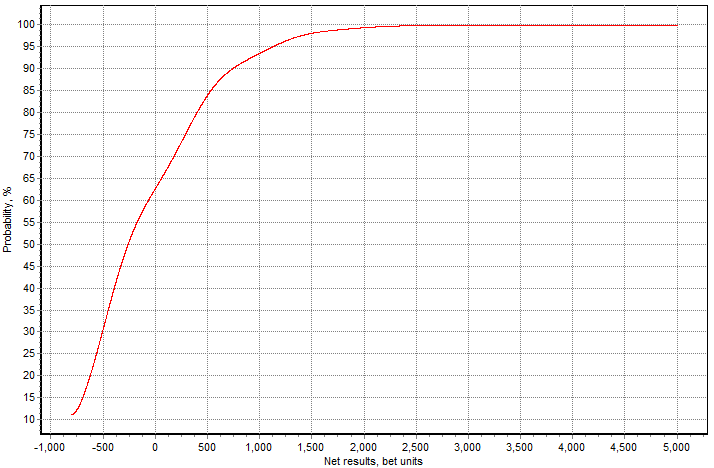
Finally here is the second graph as a CDF instead of a PDF. This is the money graph. it sumarizes what you need into a single plot simply. To find the probability youwant your bankroll to survive:
1)find that prob level on the y axis
2)track over to the curve
3)track down from there to the x axis
4)that spot on the x axis is the bankroll required (in full bets, so multiply by 5*bet level for cash requirements)

Thanks again.

It looks like my answer is 1000 or 1200 bets (5000 or 6000 coins), depending on how paranoid I'm feeling.

Thanks!