Crazy 4 Poker - Optimal Strategy

Hello everyone! I just joined this forum to make a couple posts. I have been getting interested in combinatorial statistics and gambling mathematics recently, and I wanted to find the optimal strategy for the game called Crazy 4 Poker. According to Wizard of Odds' website, the perfect strategy is extremely close to folding anything below K-Q-8-4. However extremely close is not close enough for me. After writing some code I think I have found the optimal strategy which is the following:

Raise on K-Q-8-4-3 and above
Raise on K-Q-8-4-2 if you see all four suits in your hand, bet. If K and Q are the same suits in addition to 8 and 4 being the same suits as each other, you should raise.
Raise on K-Q-7-6-5
Raise on K-Q-7-6-4 if you have cards of every suit unless you have three suits with K and Q having the same suit.

Has anyone tried to describe the perfect strategy before? And can anyone find any errors in my supposed optimal strategy?
Let me know if there are any other games you would like to see the optimal strategy for. Thanks for reading and have a nice day!

Quote: harris

Hello everyone! I just joined this forum to make a couple posts. I have been getting interested in combinatorial statistics and gambling mathematics recently, and I wanted to find the optimal strategy for the game called Crazy 4 Poker. According to Wizard of Odds' website, the perfect strategy is extremely close to folding anything below K-Q-8-4. However extremely close is not close enough for me. After writing some code I think I have found the optimal strategy which is the following:

Raise on K-Q-8-4-3 and above
Raise on K-Q-8-4-2 if you see all four suits in your hand, bet. If K and Q are the same suits in addition to 8 and 4 being the same suits as each other, you should raise.
Raise on K-Q-7-6-5
Raise on K-Q-7-6-4 if you have cards of every suit unless you have three suits with K and Q having the same suit.

Has anyone tried to describe the perfect strategy before? And can anyone find any errors in my supposed optimal strategy?
Let me know if there are any other games you would like to see the optimal strategy for. Thanks for reading and have a nice day!
link to original post

Welcome to the forum. Nice work.

Your strategy statement for K-Q-8-4-2 isn't quite complete. Should you add "Otherwise fold" for those occasions when K-Q-8-4-2 doesn't meet the stated conditions?

Why do you think there is significance for K and Q to both be the same suit?

Dear gordonm888,

Thanks for the reply.

Yes, I meant that KQ842 and KQ764 should be folded if they are not raised.

I think the exceptions involving K and Q have to do with the fact that only two types of straights / straight flushes contain either K or Q (AKQJ, KQJT, and QJT9). Most other combinations of two cards cover a lot more types of four-card straights.

BREAKING CRAZY 4 POKER NEWS
Not that anyone asked but after some mathematical research on my optimal strategy website, I found that KQ765 should be folded if there are only two suits and K and Q are different suits.

There might be other extremely minor gaps with my Crazy 4 Poker "optimal strategy" but I really don't have the motivation to find them all just yet.

This game isn’t that popular, I believe. There are a lot of Let It Ride tables, but I don’t play them very often.

I have seen plenty of Crazy 4 Poker tables at at least 10 casinos now. Because my mathematics/programming ability has improved a little, I can finally complete my analysis!


KQ932 and above: always raise

KQ843 Fold only if there are two suits total and Q and 8 are the same suit and K is of another suit

KQ842 Raise only if there are four total suits, or if there are three total suits and K/Q are the same suit

KQ832 Always fold this

KQ765 Raise if there are more than two suits or if the two suit groups are KQ7-65, KQ5-76, or KQ-765

KQ764 Raise if K/Q are the only two cards of the same suit and another suit has exactly two cards or if all four suits are represented.

KQ763 and below: always fold

The end

Please clap

I thought the game only had 4 cards. I'll have to look again.
Looks like 5 cards but only use 4 cards. https://wizardofodds.com/play/crazy-4-poker/

From the Wizard's page: https://wizardofodds.com/games/crazy-4-poker/
Optimal strategy would be tedious and complicated memorize.
However, the player can get extremely close to it with this simple strategy. Follow the first rule to apply.

Make large raise when allowed (with pair of aces or higher).
Make small raise with K-Q-8-4 or higher.
Fold all other.
The increase in house edge with the KQ84 strategy, compared to optimal, is 0.000089%.


With a Queen's Up Bet of $50 and Ante & Super Bonus bet of $30 each and a triple raise to $90 for Play on a pair of Aces or above, I'm winning $580 (plus the bet back) on a $200 bet for trips that win.
I'll update my screenshot for a triple Aces win, which is one Ace short of the Jackpot that would pay around $8.6K at these bet levels (triple those bets to hit a $25K payout limit, double again to hit the $50K payout limit).

You start with 5 cards but you only use 4 of them

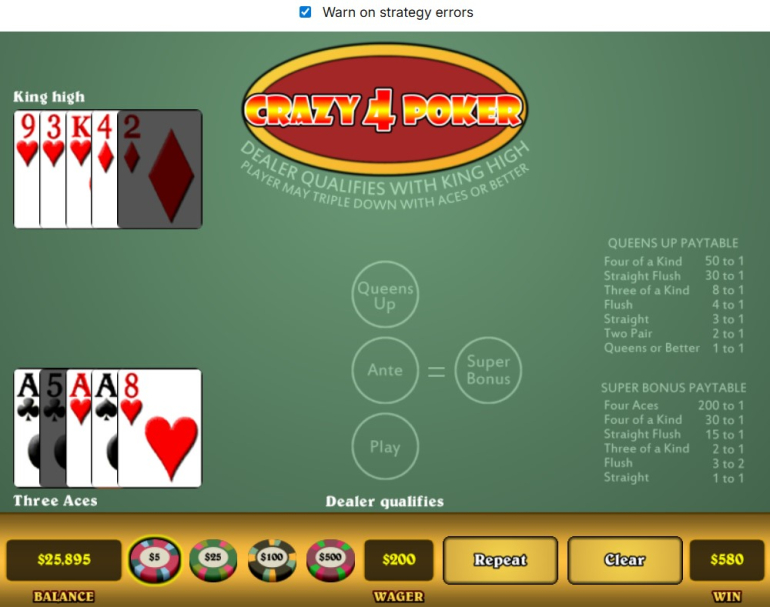
You can play the game here on my site (called Super 4 Poker - it's the AGS version)

Yes, the Wizard is right, the optimal strategy would be tedious and complicated to memorize! But I found it. I might have been the first person to truly find the optimal strategy. The second I click "post" on this comment I'm going to have a drink... I deserve it after finally ending the problem that has been bugging me for months.

I didn't write down the part about making a large raise whenever you are allowed because this was already an established part of the basic strategy.

Congratulations on optimal strategy.

Now, what if your neighbor makes a large raise and shows everyone he has an AA pair? Say an AA953? Do you fold your KJ984?

After five minutes of messing with my code I've decided I am not solving this problem tonight, and probably not until I convert all my code into C++

Sorry

Though I am going to make an educated guess that you would raise :) Though maybe the pitboss would suspect collusion ;)

I'd think the opposite, as the dealer having an ace will beat you and those are two aces he can't have.

As I recall from Grosjean's work a full collusion strategy can get you close, but it can't get you to +EV in this game.

Yeah hole carding won't really help too much either.

I do not think that this game is particularly vulnerable unless the dealer is constantly making major mistakes.

Personally I do not think this game is very interesting to play which is why I have never played it in real life, I prefer the similar game Four Card Poker because the strategy is a bit more interesting.

Hey I have an idea that might be interesting to you. Have you experienced Blackjack Switch yet?

Now that's a strategy so complex no one really knows it completely. You get two cards, and you have the option of switching the top two. What you are looking for it the pair of hands with the higher total win rate. But if you knew the win rates for all the possible hands in Blackjack Switch (someone here could probably help you with that) you could make a trainer out of it, where after the player makes their switch/no switch decision you check and see if it was the right one, and tell them the win rate of what they chose vs. the win rate of the other possibility. You could even make it a cumulative thing, where you rate a player's switching performance over time as a percentage of perfect switching strategy.

I played Blackjack Switch once after talking to the inventor. I studied the strategy for nearly an hour before I played, which paid off when I made a fairly obscure but correct switch that ended up winning me $25 (if I didn't switch, I would have lost $50).

At this point in my math journey, I can solve any game except for blackjack. Once I solve a couple blackjack-like games, it will be time for me to look at Blackjack Switch. To be honest though, I am not so motivated now that I have lots of actual math work that I get paid for. Therefore, this can be a 2027 or 2028 project ;)

Thanks for your advice, I appreciate it.

P.S. My website now tells you if you are making strategy mistakes in some games like 3 Card, I intend to implement either total-dependent or composition-dependent basic strategy for my blackjack games