Basketball probability question
What are the odds of making 2 out of 3 half-court shots? I found in a google search that 1 half court shot is 100-1.
but I am not sure if this is correct. Maybe there is someone here who knows the probability of 2 out of 3 half-court shots?
thanks
seven
edit:
I forgot to mention for the average player on a regular NBA court
Quote: sevenHey all
What are the odds of making 2 out of 3 half-court shots? I found in a google search that 1 half court shot is 100-1.
but I am not sure if this is correct. Maybe there is someone here who knows the probability of 2 out of 3 half-court shots?
thanks
seven
edit:
I forgot to mention for the average player on a regular NBA court
link to original post
About 3/10,000. Or .03%.
That’s if you postulate that the events are not correlated.
Quote: seven
I found in a google search that 1 half court shot is 100-1
edit:
I forgot to mention for the average player on a regular NBA court
link to original post
I don't believe that at all
NBA players are very strong and can easily shoot the ball that far
I would estimate on average they could make a half court shot at least one out of 15 times
if you're talking about an in game situation it would I believe be slightly less often
I played NCAA Division 1 college basketball (small college)
I believe that in my prime I could make a half court shot at least one out of 20 times
.
Quote: SOOPOOQuote: sevenHey all
What are the odds of making 2 out of 3 half-court shots? I found in a google search that 1 half court shot is 100-1.
but I am not sure if this is correct. Maybe there is someone here who knows the probability of 2 out of 3 half-court shots?
thanks
seven
edit:
I forgot to mention for the average player on a regular NBA court
link to original post
About 3/10,000. Or .03%.
That’s if you postulate that the events are not correlated.
link to original post
thank you for trying. if I understood you correctly the probability would be 3 times in 1000 tries.
please explain what you mean with > That’s if you postulate that the events are not correlated
maybe for better understanding > this challenge will be not in a game
Quote: lilredroosterQuote: seven
I found in a google search that 1 half court shot is 100-1
edit:
I forgot to mention for the average player on a regular NBA court
link to original post
I don't believe that at all
NBA players are very strong and can easily shoot the ball that far
I would estimate on average they could make a half court shot at least one out of 15 times
if you're talking about an in game situation it would I believe be slightly less often
I played NCAA Division 1 college basketball (small college)
I believe that in my prime I could make a half court shot at least one out of 20 times
.
link to original post
thank you too for trying
I am not talking about NBA players and also not in a game. this challenge is not happening in a game.
ok let's say you were or are still able to hit one half-court shot out of 20 times. But I asked the probability of 2 out of 3
Quote: sevenok let's say you were or are still able to hit one half-court shot out of 20 times. But I asked the probability of 2 out of 3
link to original post
You can figure it out for any single shot probability p
The probability of making all three = p^3
The probability of making exactly 2 out of 3 = 3 p^2 (1 - p)
Therefore, the probability of making at least 2 out of 3 = p^3 + 3 p^2 - 3 p^3 = 3 p^2 - 2 p^3 = p^2 (3 - 2p)
For p = 1/20, this is 1/400 x (3 - 1/10) = 29 / 4000, or about 1 / 138.
Quote: ThatDonGuyQuote: sevenok let's say you were or are still able to hit one half-court shot out of 20 times. But I asked the probability of 2 out of 3
link to original post
You can figure it out for any single shot probability p
The probability of making all three = p^3
The probability of making exactly 2 out of 3 = 3 p^2 (1 - p)
Therefore, the probability of making at least 2 out of 3 = p^3 + 3 p^2 - 3 p^3 = 3 p^2 - 2 p^3 = p^2 (3 - 2p)
For p = 1/20, this is 1/400 x (3 - 1/10) = 29 / 4000, or about 1 / 138.
link to original post
thanks a lot for jumping in. so it is 1 in 138 tries to get 2 out of 3 and not like member SOOPOO wrote 3/10,000
Did you take into account the 100-1 for a single shot from half court?
Quote: seventhanks a lot for jumping in. so it is 1 in 138 tries to get 2 out of 3 and not like member SOOPOO wrote 3/10,000
Did you take into account the 100-1 for a single shot from half court?
link to original post
No, the 1/138 is based on a probability of 1 in 20 for a single shot.
For 1/100, the probability of at least 2 out of 3 is 1/10,000 x (3 - 2/100) = 149 / 500,000, or 2.98 / 10,000.
Don's answer was a great one - he is extremely knowledgeable on the subject
I'm not saying what he posted was wrong - but -
in reality - this is a very difficult and strenuous shot to try
as time goes on and he keeps missing - the player's chances of making the shot will decrease due to fatigue
imo a very physically strong player would have a tremendous advantage over a thin, weaker player - even though the thin, weaker player might be a better shooter
the thin, weaker player might be able to shoot one out of 20 any time he tries just one out of 20
but if he keeps trying to make one out of 20 several times he will falter and the % of shots made will become much lower
of course, that's not something any mathematician could calculate as each player will experience and react to fatigue differently
.
Quote: ThatDonGuyQuote: seventhanks a lot for jumping in. so it is 1 in 138 tries to get 2 out of 3 and not like member SOOPOO wrote 3/10,000
Did you take into account the 100-1 for a single shot from half court?
link to original post
No, the 1/138 is based on a probability of 1 in 20 for a single shot.
For 1/100, the probability of at least 2 out of 3 is 1/10,000 x (3 - 2/100) = 149 / 500,000, or 2.98 / 10,000.
link to original post
thanks again and very much appreciated as I know Math but not like you guys :) means I need to ask till I get it
what you are saying now is 2.98 / 10.000 and this is almost same as SOOPOO with 3 / 10.000
means in 10.000 tries 3 will hit 2 out of 3
is that correct or am I wrong?
The current record holder for most half-court shots in a minute is Green Bay point guard Eric Valentin, with eight shots scored in 60 seconds. Adam Beatrice has released a video of him making ten half-court shots in a minute.
Quote: lilredrooster.
Don's answer was a great one - he is extremely knowledgeable on the subject
I'm not saying what he posted was wrong - but -
in reality - this is a very difficult and strenuous shot to try
as time goes on and he keeps missing - the player's chances of making the shot will decrease due to fatigue
imo a very physically strong player would have a tremendous advantage over a thin, weaker player - even though the thin, weaker player might be a better shooter
the thin, weaker player might be able to shoot one out of 20 any time he tries just one out of 20
but if he keeps trying to make one out of 20 several times he will falter and the % of shots made will become much lower
of course, that's not something any mathematician could calculate as each player will experience and react to fatigue differently
.
link to original post
please let me explain that a player gets only one chance to hit 2 out of 3
then another player can step up and try his luck
I am not talking about an in game challenge
Quote: MentalVince Carter entered The Guinness Book of World Records for hitting an 86-foot (26 m) shot while sitting down. No mention of fatigue.
The current record holder for most half-court shots in a minute is Green Bay point guard Eric Valentin, with eight shots scored in 60 seconds. Adam Beatrice has released a video of him making ten half-court shots in a minute.
link to original post
are you saying that he hit 8 times out of 8 tries and all one after the other in 60 seconds and all that not in an ongoing game?
edit:
ok I found the video of Adam and he missed a lot also
Quote: MentalNo mention of fatigue.
link to original post
whether or not it was mentioned - fatigue is a factor for virtually all athletes
some have much greater endurance than others
that's why even the best players are taken out of a hoops game for several minutes - so they can recover their energy
a guy who sets a record in the 100 meter dash would have exactly ZERO chance of repeating it in the same time if he tried to 5 minutes later
.
Quote: sevenwhat you are saying now is 2.98 / 10.000 and this is almost same as SOOPOO with 3 / 10.000
means in 10.000 tries 3 will hit 2 out of 3
is that correct or am I wrong?
link to original post
That is correct. Of course, that makes the assumption that every shot has a 1 / 100 chance of being made.
I would like to see how many shots is needed to see a two goals in a row.
Quote: ThatDonGuyQuote: sevenwhat you are saying now is 2.98 / 10.000 and this is almost same as SOOPOO with 3 / 10.000
means in 10.000 tries 3 will hit 2 out of 3
is that correct or am I wrong?
link to original post
That is correct. Of course, that makes the assumption that every shot has a 1 / 100 chance of being made.
link to original post
Thank you for your confirmation and clarification.
but what do you think of @aceside's post?
He wrote
I believe this is inaccurate. In 10,000 tries of 3-shot sets, at least 2 of each 3 shots will hit.
I would like to see how many shots is needed to see two goals in a row.
Quote: acesideI believe this is inaccurate. In 10,000 tries of 3-shot sets, at least 2 of each 3 shots will hit.
I would like to see how many shots is needed to see a two goals in a row.
link to original post
yes interesting question, thanks
Quote: sevenThank you for your confirmation and clarification.
but what do you think of @aceside's post?
He wrote
I believe this is inaccurate. In 10,000 tries of 3-shot sets, at least 2 of each 3 shots will hit.
I would like to see how many shots is needed to see two goals in a row.
link to original post
I don't understand his answer. I have a feeling he misunderstood the question.
Quote: ThatDonGuyQuote: sevenThank you for your confirmation and clarification.
but what do you think of @aceside's post?
He wrote
I believe this is inaccurate. In 10,000 tries of 3-shot sets, at least 2 of each 3 shots will hit.
I would like to see how many shots is needed to see two goals in a row.
link to original post
I don't understand his answer. I have a feeling he misunderstood the question.
link to original post
oh ok so let's see if he can shed some light on his input.
This is interesting. If there are 2 or more goals in a row, there must be at least 2 goals in a 3-shot trial.
Quote: acesideI posted to learn from ThatDonGuy. I just wanted to participate. If the probability of one successful goal is 1/100, a player needs to make 100x101= 10100 shots to see a 2-or-more-consecutive-goal event.
This is interesting. If there is a 2 or more-goal event in a row, there must be at least 2 goals in a 3-shot trial.
link to original post
yes it is 2 out of 3 which means as soon the player does 2 in a row he will not need to do the 3rd shot
Quote: acesideIt looks like this question is slightly different from your original one. We need ThatDonGuy.
link to original post
yes we need Don but I still did not understand your question. Please give it ELI5, thanks
The calculation is
100 + 100^2 = 10100.
E(Xk) = (1 − p^k)/((1 − p)p^k), where p is the probability of success for an individual event, and k is the streak length.
Var(Xk) = (1 − (2k + 1)(1 − p)p^k − p^(2k+1))/((1 − p)^2p^(2k))
Punch those equations into Wolfram Alpha, like so:
(1 − p^k)/((1 − p)p^k), p = 1/100, k = 2
and you get E(Xk) = 10100, and Var(Xk) = 101979900, or a standard deviation of ~3461 shots
I also agree that 1/100 is way too low; I had a high school friend who was a scrub on the basketball team, but could hit half court shots maybe 1/8 or 1/10.
Quote: TaxrBuxI agree with aceside. Here's a link (https://mathcs.pugetsound.edu/~mspivey/Paper-kConsecutive_Revision_2final.pdf) to a paper that mentions these equations for calculating streak probabilities:
E(Xk) = (1 − p^k)/((1 − p)p^k), where p is the probability of success for an individual event, and k is the streak length.
Var(Xk) = (1 − (2k + 1)(1 − p)p^k − p^(2k+1))/((1 − p)^2p^(2k))
Punch those equations into Wolfram Alpha, like so:
(1 − p^k)/((1 − p)p^k), p = 1/100, k = 2
and you get E(Xk) = 10100, and Var(Xk) = 101979900, or a standard deviation of ~3461 shots
I also agree that 1/100 is way too low; I had a high school friend who was a scrub on the basketball team, but could hit half court shots maybe 1/8 or 1/10.
link to original post
can you please say same in simple numbers? what is the probability of 2 out of 3 and 2 out of 2 for an average player
is it 1 in 1000 tries or 1 in 3000 or whatever?
thanks for jumping in
Quote: TaxrBuxFor the answer to your original question, ThatDonGuy gave the answer already. You can play with the numbers yourself by googling a binomial distribution statistics calculator, and entering the probability, number of total events, and number of successes to figure out good odds/bets. The more accurate your estimate of the individual probability of success, the better the estimate of 2 out of 3 or whatever will be. For example, with a roll of 5 dice, getting 2 or more sixes, you can get an exact probability, whereas with an "average" pro basketball player's ability to hit a half court shot, you need a lot more research to be confident in your estimate.
link to original post
Yes Don gave already the answer and I thought that's it. But then all the other answers confused me. I iwll google what you told me and let's see if I can mange it. thanks
If the probability of making the half-court shot is 50-1, or 2 percent.
the probability of making exactly 2 out of 3 half-court shots is 0.00117600 or approximately 0.12%.
If the probability of making the half-court shot is 100-1, or 1 percent.
the probability of making exactly 2 out of 3 half-court shots is 0.00029700 or approximately 0.03%.
please let me know if this is ok or I did a mistake
In any case, thank you all for the very helpful and polite discussion.
seven
Quote: sevenok I googled for a binomial distribution statistics calculator and found one and the result was for 2 out of 3 (if I did it correctly)
If the probability of making the half-court shot is 50-1, or 2 percent.
the probability of making exactly 2 out of 3 half-court shots is 0.00117600 or approximately 0.12%.
If the probability of making the half-court shot is 100-1, or 1 percent.
the probability of making exactly 2 out of 3 half-court shots is 0.00029700 or approximately 0.03%.
please let me know if this is ok or I did a mistake
In any case, thank you all for the very helpful and polite discussion.
seven
link to original post
Yes, you got that right so far as you went. Every spreadsheet includes the binomial formula.
=BINOMDIST(2,3,0.01,false) = 0.0002970Quote: google sheets
=BINOMDIST(num_successes, num_trials, prob_success, cumulative)
Example
BINOMDIST(3, 7, 0.5, TRUE)
Calculates the probability of drawing a certain number of successes (or a maximum number of successes) in a certain number of tries given a population of a certain size containing a certain number of successes, with replacement of draw
=BINOMDIST(2,3,0.02,false) = 0.0011760
But, I assume that making 3 of 3 shots would also win the contest. This adds another 0.0000080 to the second result. Since the exact probability of making a shot is very uncertain, failure to include the small probability of 3 for 3 hardly makes you answer invalid.
Quote: sevenHey all
What are the odds of making 2 out of 3 half-court shots? I found in a google search that 1 half court shot is 100-1.
but I am not sure if this is correct. Maybe there is someone here who knows the probability of 2 out of 3 half-court shots?
thanks
seven
edit:
I forgot to mention for the average player on a regular NBA court
link to original post
Sorry for the late arrival.
Wikipedia says, "Collectively, NBA players try shots from beyond half-court a few hundred times each season; approximately 1 in 100 of those shots are made. "
The probability of making exactly two out of three is 3*(1/100)^*(99/100) = 0.000297 = 1 in 3367.
The probability of making at least 2 out of 3 is 0.000298 = 1 in 3355.7.
Quote: WizardQuote: sevenHey all
What are the odds of making 2 out of 3 half-court shots? I found in a google search that 1 half court shot is 100-1.
but I am not sure if this is correct. Maybe there is someone here who knows the probability of 2 out of 3 half-court shots?
thanks
seven
edit:
I forgot to mention for the average player on a regular NBA court
link to original post
Sorry for the late arrival.
Wikipedia says, "Collectively, NBA players try shots from beyond half-court a few hundred times each season; approximately 1 in 100 of those shots are made. "
The probability of making exactly two out of three is 3*(1/100)^*(99/100) = 0.000297 = 1 in 3367.
The probability of making at least 2 out of 3 is 0.000298 = 1 in 3355.7.
link to original post
‘BEYOND HALFCOURT’ includes many shots WAY beyond halfcourt, making them MUCH harder than just ‘halfcourt’. Those NBA shots are virtually always with the player moving making them MUCH harder than a ‘standing still’ type shot. (Players will still move forward during the shot). And, the opposing team will try and alter/defend the shot. No way for me to know, but I’d guess certain players, like Doncic, Lillard, Curry, would far exceed 1% on an unguarded half court shot. And others, like Robinson, Drummond, Gobert would be far less likely than 1% to hit the shot.
In Medical School, SOOPOO once hit two consecutive halfcourt shots. Now I can’t take a normal shot from half court due to lack of strength.
Quote: WizardQuote: sevenHey all
What are the odds of making 2 out of 3 half-court shots? I found in a google search that 1 half court shot is 100-1.
but I am not sure if this is correct. Maybe there is someone here who knows the probability of 2 out of 3 half-court shots?
thanks
seven
edit:
I forgot to mention for the average player on a regular NBA court
link to original post
Sorry for the late arrival.
Wikipedia says, "Collectively, NBA players try shots from beyond half-court a few hundred times each season; approximately 1 in 100 of those shots are made. "
The probability of making exactly two out of three is 3*(1/100)^*(99/100) = 0.000297 = 1 in 3367.
The probability of making at least 2 out of 3 is 0.000298 = 1 in 3355.7.
link to original post
Better late than never :) Thank you very much for taking part in this discussion with your valuable opinion.
I never thought I would find information on my question in Wikipedia. Learned something again.
Again, thanks to all of you for your input that has helped me get the answer I was looking for.
seven
perhaps the most famous shot in the history of the NBA
60 footer from beyond half court to put the Finals game against the Knicks into OT -
one of the amazing things about the shot was that a Knicks player, Willis Reed, was right in West's face when he took the shot and he almost blocked it
the Lakers still lost the game and the series to the Knicks
West, who had the nickname "Mr. Clutch" was for a very long time my fave player
he was so very great
.
.
.
According to the article How Mapping Shots In The NBA Changed It Forever, the probability of making a 3-point shot is 36%.
The distance of the 3-point line is 23' 9".
The distance of the half-court line is 47'.
I figure the probability of making the shot is inversely proportional to the square of the distance. That would make my estimate:
0.36 * (23.75/47)^2 = 9.19%.
This seems too high.
I welcome all thoughts.
Quote: Wizard
I was thinking more about the probability of an NBA player making a half court shot.
According to the article How Mapping Shots In The NBA Changed It Forever, the probability of making a 3-point shot is 36%.
The distance of the 3-point line is 23' 9".
The distance of the half-court line is 47'.
I figure the probability of making the shot is inversely proportional to the square of the distance. That would make my estimate:
0.36 * (23.75/47)^2 = 9.19%.
This seems too high.
I welcome all thoughts.
link to original post
it is too high because the player has to shoot the ball much harder to get it to go that distance
the player cannot maintain anywhere near the accuracy for the much longer distance than a 3 point shot
most players shoot a jump shot from over their heads to make a 3 pointer - it's very routine
to shoot it 47 feet they can't shoot like that - they will have to push the ball from about chest high - it will be a much more inaccurate shot
if your calculation were true - I can't do the math - but I'm estimating it might come out to be 4% for a 70 foot shot
and to shoot a 70 foot shot most players would have to throw the ball like it was a baseball - they don't have much of a prayer of getting it in
.
I suspect there is some study or literature on this as it should be similar to the issue of how likely a ballistic missile or catapult will hit a target at varying distances.
ETA: LR makes another good point about technique being different for a human catapult at varying distances.
Here is a video of a girl making nine half court shots in a row.
https://www.guinnessworldrecords.com/world-records/96785-most-consecutive-basketball-half-court-shots#:~:text=The%20most%20consecutive%20basketball%20half,USA%2C%20on%205%20September%202023.
If a NBA star had a motivation to practice this shot, I think they would eventually get to 15%. Throwing a ball into a hole is not that hard. Tom Amberry holds a Guinness World Record for making 2,750 consecutive free throws.
.7 * (15/23.75)^2 = 27.9% (average players)
.9 * (15/23.75)^2 = 35.9% (elite players)
Is it more linear?
.7 * (15/23.75) = 44.2% (average players)
.9 * (15/23.75) = 56.8% (elite players)
It looks pretty close to linear. But at some point, the biomechanics kick in to cause the curve to dip. Much more leg is required for a half court shot compared to a three-point shot. The 9% figure doesn't sound too high for a practiced shot. Players don't work on their half court technique much compared to free throw and jumper technique.
Quote: TaxrBuxThe average free throw percentage is ~70%, with elite shooters at 90%+. That's a 15-ft shot, usually taken with all arms. Three-point shots taken in-game are most often contested. For uncontested shots, see the annual All Star Game three-point shooting competition. The average percentage in that competition is 52.8%, by the elite three-point shooters in the league. Three-point shots all involve some amount of leg power. Using the square of the distance with these numbers shows that distance is less of a factor than you would think, at least in the range of using arm power and some leg power.
.7 * (15/23.75)^2 = 27.9% (average players)
.9 * (15/23.75)^2 = 35.9% (elite players)
Is it more linear?
.7 * (15/23.75) = 44.2% (average players)
.9 * (15/23.75) = 56.8% (elite players)
It looks pretty close to linear. But at some point, the biomechanics kick in to cause the curve to dip. Much more leg is required for a half court shot compared to a three-point shot. The 9% figure doesn't sound too high for a practiced shot. Players don't work on their half court technique much compared to free throw and jumper technique.
link to original post
Good post.
Had another thought if Wiz still wants to make a model. Linear distance to the hoop isn’t really the relevant distance, it’s the increase in distance that the basketball has to travel to the hoop during its ballistic parabola.
Quote: WizardI was thinking more about the probability of an NBA player making a half court shot.
According to the article How Mapping Shots In The NBA Changed It Forever, the probability of making a 3-point shot is 36%.
The distance of the 3-point line is 23' 9".
The distance of the half-court line is 47'.
I figure the probability of making the shot is inversely proportional to the square of the distance. That would make my estimate:
0.36 * (23.75/47)^2 = 9.19%.
This seems too high.
I welcome all thoughts.
link to original post
Okay
I'm curious - for the Wizard and any other brilliant math guys -
if an NBA player can make a one foot shot - 95% of the time - which I'm sure he could - this is a shot - not a layup or dunk where he's right at or over the rim
using the Wizard's calculation - what is the probability that he can make a 3 point shot_________?
and also what is the probability that he can make a foul shot - 15 feet out_________?
thanks
.
Quote: lilredroosterOkay
I'm curious - for the Wizard and any other brilliant math guys -
if an NBA player can make a one foot shot - 95% of the time - which I'm sure he could - this is a shot - not a layup or dunk where he's right at or over the rim
using the Wizard's calculation - what is the probability that he can make a 3 point shot_________?
and also what is the probability that he can make a foul shot - 15 feet out_________?
thanks
.
link to original post
By my method explained in my last post, those answers would be 10.6% at 3 feet and 0.4% at 15 feet. Clearly unrealistic.
I think looking at ballistics would be better to get at the issue of estimating shot accuracy by distance. For example, if a Marine sharpshooter has a 50% chance of hitting a target at a distance of d, what is the probability at 2d?
Quote: TaxrBux. The 9% figure doesn't sound too high for a practiced shot. Players don't work on their half court technique much compared to free throw and jumper technique.
yes, but consider Mental's point -
the ball can still go in if it hits the rim and/or backboard on a free throw or 3 point shot
not so on a half court shot
it's almost certainly going to bounce off the rim and/or the backboard with rare exceptions
the half court shooter is going to pretty much have to shoot a swish - very, very difficult
.
Quote: lilredroosterQuote: TaxrBux. The 9% figure doesn't sound too high for a practiced shot. Players don't work on their half court technique much compared to free throw and jumper technique.
yes, but consider Mental's point -
the ball can still go in if it hits the rim and/or backboard on a free throw or 3 point shot
not so on a half court shot
it's almost certainly going to bounce off the rim and/or the backboard with rare exceptions
the half court shooter is going to pretty much have to shoot a swish - very, very difficult
link to original post
In the video of 9 straight half court shots that I posted, only three were swishes. None hit the front of the rim. Low arcing shots tend to hit the back of the rim a lot. You might be able to graze the front of the rim, but any solid contact with the front of the rim almost guarantees a miss when the ball is moving at high speed. It is hard to have a soft touch from half court.
My wife can stand one foot away from a basket and will shoot at a rate of 0.00000%. She is tiny and literally cannot throw the ball high enough to reach the rim. So, you would need to define a standard man/person or a standard basketball player.
In general the drag on an object (through air) is proportional to v3 (where v = velocity) so the harder and faster you throw a basketball over long distances the greater the drag - which will be a source of variance in distance, height and horizontal accuracy.
The discussion of accuracy versus distance is more tractable for throwing a football.
- the throwing motion is the same for all distances
- the football is more aerodynamic than the basketball, less drag
- Joe Milton, an NFL rookie QB, can literally stand in one endzone and (barely) reach the other endzone with an all-out heave. But that's about it for distance, currently.
Quote: gordonm888Consider the percentage from the other extreme: the success percentage from >100 yards is 0.00000%. So, the relationship between successfully making a shot and distance, r, cannot be 1/rn.
My wife can stand one foot away from a basket and will shoot at a rate of 0.00000%. She is tiny and literally cannot throw the ball high enough to reach the rim. So, you would need to define a standard man/person or a standard basketball player.
In general the drag on an object (through air) is proportional to v3 (where v = velocity) so the harder and faster you throw a basketball over long distances the greater the drag - which will be a source of variance in distance, height and horizontal accuracy.
The discussion of accuracy versus distance is more tractable for throwing a football.
- the throwing motion is the same for all distances
- the football is more aerodynamic than the basketball, less drag
- Joe Milton, an NFL rookie QB, can literally stand in one endzone and (barely) reach the other endzone with an all-out heave. But that's about it for distance, currently.
link to original post
Sorry if this sounds stupid, but I don't understand what you're trying to say. A basketball court is 30.62 yards long. A half-court shot is at least 15.31 yards.
What do you think the probability is for an average player or person to hit a half court shot?
thanks
The drag force is F=1/2 C ρ A v2 where C is the drag coefficient, A is the area of the object facing the fluid, and ρ is the density of the fluid, so force is not proportional to v3. The distance a ballistic object travels is proportional to sqrt(v) ignoring drag. So the drag force is only linear in distance. The total energy expended to fight drag increases as distance squared (E = force * distance).Quote: gordonm888Consider the percentage from the other extreme: the success percentage from >100 yards is 0.00000%. So, the relationship between successfully making a shot and distance, r, cannot be 1/rn.
My wife can stand one foot away from a basket and will shoot at a rate of 0.00000%. She is tiny and literally cannot throw the ball high enough to reach the rim. So, you would need to define a standard man/person or a standard basketball player.
In general the drag on an object (through air) is proportional to v3 (where v = velocity) so the harder and faster you throw a basketball over long distances the greater the drag - which will be a source of variance in distance, height and horizontal accuracy.
The discussion of accuracy versus distance is more tractable for throwing a football.
- the throwing motion is the same for all distances
- the football is more aerodynamic than the basketball, less drag
- Joe Milton, an NFL rookie QB, can literally stand in one endzone and (barely) reach the other endzone with an all-out heave. But that's about it for distance, currently.
link to original post
Yes, C is lower for a football versus a basketball and has a lower frontal area.
Quote: MentalThe drag force is F=1/2 C ρ A v2 where C is the drag coefficient, A is the area of the object facing the fluid, and ρ is the density of the fluid, so force is not proportional to v3. The distance a ballistic object travels is proportional to sqrt(v) ignoring drag. So the drag force is only linear in distance. The total energy expended to fight drag increases as distance squared (E = force * distance).
Yes, C is lower for a football versus a basketball and has a lower frontal area.
link to original post
Sorry, I misspoke, I meant that the power needed to overcome the drag force is proportional to v3:
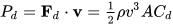For example, the gasoline usage in a car moving at constant velocity depends upon the tire friction and the air drag and the power(gasoline combustion) to overcome the air drag is proportional to v3.My point was that the effort/energy for an NBA player to throw a ball a distance x is not linearly proportional to x because the energy to overcome the air drag is proportional to v3 -and because a higher velocity is required to throw a ball a longer distance
The energy imparted to the basketball to make a shot of a certain distance is actually less than proportional to distance ignoring drag. Making a shot from two feet or three feet requires almost the same amount of energy because most of the energy is need to get the ball from your release height to the rim height. Drag barely matters at distances up to half court, so the energy/effort actually increases less than proportionately to distance of the shot. Energy going into drag will eventually matter at long distances, since it increases faster than linearly with distance.Quote: gordonm888Quote: MentalThe drag force is F=1/2 C ρ A v2 where C is the drag coefficient, A is the area of the object facing the fluid, and ρ is the density of the fluid, so force is not proportional to v3. The distance a ballistic object travels is proportional to sqrt(v) ignoring drag. So the drag force is only linear in distance. The total energy expended to fight drag increases as distance squared (E = force * distance).
Yes, C is lower for a football versus a basketball and has a lower frontal area.
link to original post
Sorry, I misspoke, I meant that the power needed to overcome the drag force is proportional to v3:
My point was that the effort/energy for an NBA player to throw a ball a distance x is not linearly proportional to x because the energy to overcome the air drag is proportional to v3 -and because a higher velocity is required to throw a ball a longer distance
link to original post
Ignoring drag and the difference between the release height and the rim height, range is given by R = v02 sin(2θ) / g. This is quadratic in velocity and so is the energy/effort. So energy increases linearly with distance.
