Thread Rating:
Dice control is a throwing technique that, when done right, reduces the randomness of each die to be one of 4 sides, thus eliminating 20 of the 36 possible outcomes of each roll.
Dice setting is relatively simple. It's just how you position the dice so that if the controlled throw is successful, you know which 20 outcomes are eliminated. It's a relatively worthless technique if you can't do the controlled throw.
But there absolutely is still a lot of randomness to it. For one thing, no matter what you do, the dice will be rotating while in the air.
The key to dice control is to keep the dice rotating 'On Axis', both in the air, and once they hit the table. It doesn't matter if the dice bounce or roll, although obviously, the more they do, the more likely that they won't remain on axis. If they roll forward, no problem. If they roll onto their side, you've got problems.
Dead dice, so that they land without any bounce or additional roll, is an even harder goal to achieve, but one dice control aficionados tend to talk about.
But I get the feeling that some people don't know what 'On Axis' means. Put simply, it's to imagine that the dice are attached to a spindle (or that the two touching faces are glued together) so they only roll in a specific predictable rotational direction, and that the result is one out of the four rotating faces rather than any of the six faces.
To illustrate:
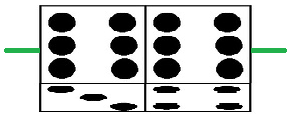
In these dice, the axis goes through the 2-5 faces of both dice. The sixes are parallel.
The sixes are on top, ones on the bottom, and threes and fours on the front and back. It doesn't matter if the front faces are the same or not. If they can be kept rotating along the green axis line (regardless of whether they stay together), each die will be limited to a result of 1, 3, 4 or 6. Sixteen total combinations, four of which is seven.
Yes, that means MORE sevens than normal. But that's acceptable, and desirable, on the come out roll.
Turn one die as shown here:
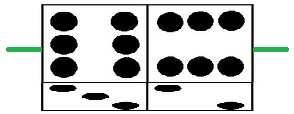
Now the sixes are perpendicular. The turned die should only result in 1, 2, 5, or 6, while the other should still be 1, 3, 4, or 6. There are now only two ways to roll a seven, out of sixteen combinations.
For those that like charts, here's all six:
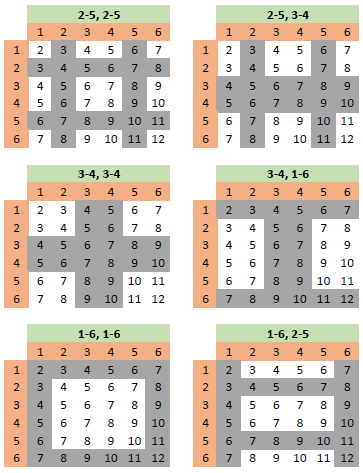
The green header indicates which faces are on the axis. Their results are greyed out of the chart.
The top left chart is for the dice aligned like the first picture above, where the axis is 2-5 on both. The top right chart is for the second picture. The axis is 2-5, 3-4.
The easy way to align the dice is with the twos on top for the second set of charts, and threes on top for the third. The left side with them parallel, the right is perpendicular, also called a "Flying V".
Note that when the tops are parallel, you do need to check the front faces, or axis faces, if you have a preference for a specific chart. But with a little experience, you'll know which way the tops face when parallel for your desired chart.
You're probably asking why I said "desired chart." That's the Dice Setting part.
Put simply, if you're a pass line shooter, you'd want one of the charts on the left for the come out, since they increase the odds of a come out 7, then one on the right with its reduced odds of a 7 out.
Let's think about after the point is established first. All three sets on the right have two chances each of a 5 or 9. The top and bottom have one chance of a 4 or 10. The bottom has three chances each for 6 or 8.
Are you also a hard way person? The 2-5, 3-4 eliminates all hard ways, while the 3-4, 1-6 allows the hard 4 & 10, and the 1-6, 2-5 has the hard 6 & 8.
So what's your desired point? If it's 4 or 10, use the 2-5, 2-5 on the come out roll. If the point IS 4 or 10, use the 3-4, 1-6 on following rolls.
Looking for a 5 or 9? Use either the 2-5, 2-5 or 1-6, 1-6 set to come out, then any perpendicular set to hit it.
6 or 8? Use 1-6, 1-6 to come out, then 1-6, 2-5 afterwards.
Some people think dice control is about reducing the chances of a 7 after the come out. As you can see by the charts, that's part of it.
But if you're serious about it, when you try to do this, or even when you practice, instead of tracking the number of 7s, for whichever dice set you choose, track how many times your roll landed on a grey number or white number on my chart. THAT will tell you if you're at all successful.
Obviously, there's a lot to think about and a lot to consider.
But the most important part is getting those damn dice to stay on axis. A skill which I believe is impossible. Or damn near it.
In a perfect world, you could throw a die on a horizontal axis onto a perfectly flat table. The die could never tumble right or left because this would break the mirror symmetry of the starting conditions. (Google symmetry breaking in physics for examples.)
In the real world, it would be easy to send a die on to a perfect felt with 1 to the right and 6 to the left by firing it from a mechanical device. For extremely slow, short mechanical throws, you would have a lot of die control. At some faster speed, the die moves slightly off axis on one contact on the felt and then more on the next contact. If a machine cannot fire the die in such a way that these off-axis movements don't grow rapidly at real-world craps distances, then no human can do it either.
Until someone shows me that a machine can control the die on a flat felt without a back wall, I won't spend much time thinking about human dice control.
Study One
This one is a probability study done by UNLV to see how much control you would really need to break even with the house. They found you would need to have 8% control to break even (0% is completely random and 100% is perfect control and rotation).
Study Two
This is by the same author and used a mechanical machine to test repeated throws that mimic "controller" throws (had backspin and moved in an arc) that gave very precise and repeatable throw conditions. They found that with legal throws that hit the backwall every time, there was no statistical change compared to what is expected with random throws.
I still set my dice in the casino for fun but I don't think there's any hope for actual setting for profit.
Quote: MDawgI can definitely and verifiably control a dice roll for a few inches, such as on a Monopoly board. Been able to do that since I started playing the game as a child. I am fairly consistent on a backgammon board too but the hardness of the board, I play on a real wood set, makes it harder for sure as the dice will tend to bounce more.
So I'd think that yes, on a regular craps felt, if didn't have to hit the back wall and didn't have to throw for very far, would be possible too. But I don't know of any casino that would allow that. Assuming a standard 12 foot craps table it just seems odd that any casino would allow rolls of a mere 2 feet.
link to original post
When I do it over very short distances all it's about is setting the dice and rolling in exactly the same controlled way, such that the dice roll exactly the same way over exactly the same distance or close. I'm not thinking about axes or anything much beyond that, although yes - that's what is happening, as to how or why the dice might keep ending up the same way. Obviously it doesn't work every time, but over a few inches it works enough to make a big difference.
I assume that anyone who practices dice control does the same thing - try to roll exactly the same way over exactly the same distance. Over a few inches, especially on a relatively soft surface like a cardboard board game, it can work.
The longer the distance of the roll, the more unlikely the predictable outcome. Add a back wall bounce requirement, especially after a 10 foot or so roll, and it becomes highly improbably to control the outcome in any meaningful way.
assuming the table limits will be what I expect, I'm still sticking to my plan to go totally darkside next time. I was going to try to avoid rolling the dice myself, but maybe I'll change my mind. And at where I'll be, sometimes during the week you have to be the shooter, you're the only one at the table.
If a darkside shooter, and you want to set the dice*, I already knew the flying V was the way to go for the Come-out. It can be set quickly and if the dice stay on axis, there are only two ways 7 can be rolled. But for subsequent rolls after a point has been set, I had just gone to random roll, nothing set.
Now I can see various axes should be the way to go for resolving points. Sometimes there are 4 ways to roll a 7 and, if both axes on 1-6 or both on 3-4, one way to roll a 10 or a 4. The Darksiders don't want to lose those if the point. Both on 2-5 will give you 4 possible 7s while limiting a bit 5,6,8, or 9
Thank you, DJ! should be fun!

* just for fun in my case
This is a link to a study done by a now defunct firm. I highly recommend reading it but I will break down some of the key points below.
https://web.archive.org/web/20050415011037/www.sunzeri.com/TrueCraps/TC-DiceControl.htm
Quote:Just a rough estimate for a non-spin movement using a mass of 7 grams, a 45-degree angle, and acceleration of 5 m/s2, and 4 cm per revolution.
T=[m x g x sin(theta)] / (revs x 2 x pi)
T=[7 x 5 x .707] / (25 x 2 x 3.141)
T=[24.754]/157.05
T= .157561 newton/meters
They calculated the amount of force needed to act on a die to turn it up onto a point as 0.15761 newton/meters.
As we all know a standard craps table is 12 feet long with a realistic playing area on the layout that is more like 11 feet 10 inches (3.3528 meters) . You are never throwing from that extreme though so if we charitably give the player the spot next to the stick and only have them throw 5.75 feet (1.7526 meters) then you are throwing the dice with a force of acceleration that would be no lower than 1.7526 m/s^2.
The standard casino die is 7 grams. F=m * a
F = 7 * 1.7526
F = 12.2682 Newtons
By my math the amount of force imparted by a throw at the most favorable position for an aspiring dice controller is approximately 77 times more force needed than the amount needed to turn a die onto its point. You would need a perfect throw every time to avoid any landing deviation that would allow that force to turn the die. Of course all of this math obviates the requirement of hitting the alligator bumps on the walls.
Feel free to check my math. I know the site uses 5m/s^2 as its force but I find that to be excessive given the length of a standard craps table.
I agree with the conclusion but, I have problem with your presentation. Force is measured in newtons, not N/m. The acceleration during the throw is not important to the physics when the dice land: only the velocity and angular momentum are important.Quote: AitchTheLetterThe idea behind dice control, in a vacuum, is an intriguing one. However the physics of the whole system don't really allow any meaningful control unless you can throw (or loft, whatever word you want to use) the dice significantly softer than the average person.
This is a link to a study done by a now defunct firm. I highly recommend reading it but I will break down some of the key points below.
https://web.archive.org/web/20050415011037/www.sunzeri.com/TrueCraps/TC-DiceControl.htm
Quote:Just a rough estimate for a non-spin movement using a mass of 7 grams, a 45-degree angle, and acceleration of 5 m/s2, and 4 cm per revolution.
T=[m x g x sin(theta)] / (revs x 2 x pi)
T=[7 x 5 x .707] / (25 x 2 x 3.141)
T=[24.754]/157.05
T= .157561 newton/meters
They calculated the amount of force needed to act on a die to turn it up onto a point as 0.15761 newton/meters.
As we all know a standard craps table is 12 feet long with a realistic playing area on the layout that is more like 11 feet 10 inches (3.3528 meters) . You are never throwing from that extreme though so if we charitably give the player the spot next to the stick and only have them throw 5.75 feet (1.7526 meters) then you are throwing the dice with a force of acceleration that would be no lower than 1.7526 m/s^2.
The standard casino die is 7 grams. F=m * a
F = 7 * 1.7526
F = 12.2682 Newtons
By my math the amount of force imparted by a throw at the most favorable position for an aspiring dice controller is approximately 77 times more force needed than the amount needed to turn a die onto its point. You would need a perfect throw every time to avoid any landing deviation that would allow that force to turn the die. Of course all of this math obviates the requirement of hitting the alligator bumps on the walls.
Feel free to check my math. I know the site uses 5m/s^2 as its force but I find that to be excessive given the length of a standard craps table.
link to original post
You can calculate the minimum energy with which a die lands when thrown from a certain height and distance to the first contact with the felt. You can compare that to the energy needed to lift the die enough to turn it up onto a point. These will be much simpler calculations and the ratio will be large. I don't have time to work up the numbers now. However, the calculations are simpler working with the energy ratios rather than force and momentum.
The real question is how much force or energy does it take to get a die off of the throwing axis. If the assumption is that the whole setup has perfect right/left symmetry, then any calculation will have the die ending up on axis.
My assumption is that anything other that a 100% perfectly symmetrical toss would likely end up with the dice rolling as normal instead of as set by the shooter. I do not think anyone can realistically throw the dice 100% symmetrically every time or enough to overcome the inherent house edge.
I absolutely agree with this last assertion. When the dice are in hand, they are not level. When they leave the hand, they are never spinning on a perfect horizontal axis. The machine that was built to do this far better than a human still could not avoid nearly perfect randomness for real-world distance.Quote: AitchTheLetterThe math in the quotation box is purely from the source. I agree doing all the math right is needed, right now I do not have the time.
My assumption is that anything other that a 100% perfectly symmetrical toss would likely end up with the dice rolling as normal instead of as set by the shooter. I do not think anyone can realistically throw the dice 100% symmetrically every time or enough to overcome the inherent house edge.
link to original post
Quote: MentalNice explanation.
In a perfect world, you could throw a die on a horizontal axis onto a perfectly flat table. The die could never tumble right or left because this would break the mirror symmetry of the starting conditions. (Google symmetry breaking in physics for examples.)
In the real world, it would be easy to send a die on to a perfect felt with 1 to the right and 6 to the left by firing it from a mechanical device. For extremely slow, short mechanical throws, you would have a lot of die control. At some faster speed, the die moves slightly off axis on one contact on the felt and then more on the next contact. If a machine cannot fire the die in such a way that these off-axis movements don't grow rapidly at real-world craps distances, then no human can do it either.
Until someone shows me that a machine can control the die on a flat felt without a back wall, I won't spend much time thinking about human dice control.
link to original post
Ding ding ding coo coo coo (making bird call noises) calling Mark Rober, Mr Rober please report to the front desk. Mr Mark Rober your skills and expertise is needed. No more beating arcades and bowling, time to beat the casino Mr Rober!
So I added another set of charts:
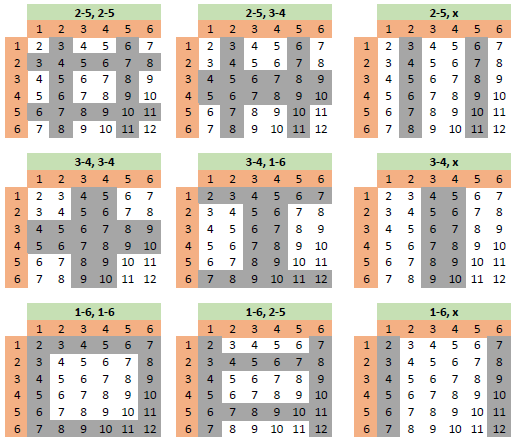
I then started looking at them, particularly that "1-6, x" chart. 6 or 8 occurs just as often as a 7, but pays as if it hits less often. That becomes a player advantage. There are probably other player advantage combinations here.
So I did the math. Holy crap! Check out these percentages:
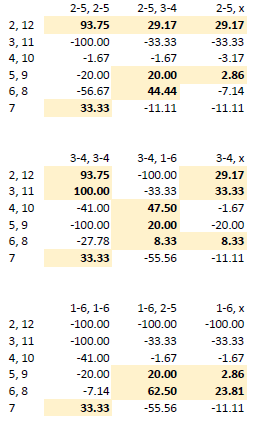
Negative numbers are the house edge, Positives are player advantage.
Note that the math I did is based on the following bets and payouts:
Prop bets on the 2/12 and 3/11 that pays 30 to 1 or 15 to 1.
Buy the 4/10 paying the vig on a win.
Place the 5/9, 6/8.
Hop the 7s paying 13 to 3.
Note that I didn't bother to calculate a pass bet with odds. Even without dice control, that math is horribly complex. Suffice to say that if the place bet has a positive advantage, the pass & odds does as well.
Some of those player advantages are so huge, that you don't need a lot of accuracy with the controlled dice throw to change the odds in your favor.
And it also shows some obvious strategies, such as: Come out using the 3-4, 3-4 set along with money on the horn and/or hopping 7. 10 out of 16 will pay! And the other six? Those are points which you can figure out which set to use to give you a better chance of hitting.
I'd like to remind people that I really don't give much credence to dice control. But if you can influence the dice just a bit, you can swing the house edge in your favor.
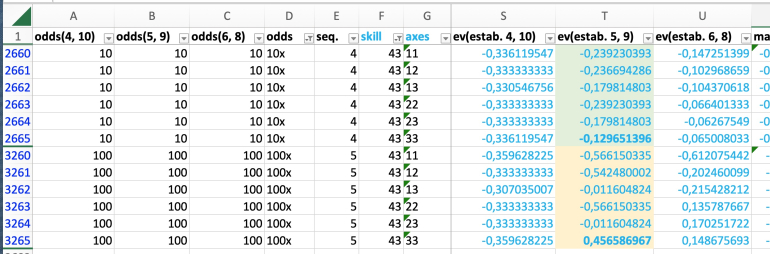
The graph for the expected value over the full range of skill levels looks like this:
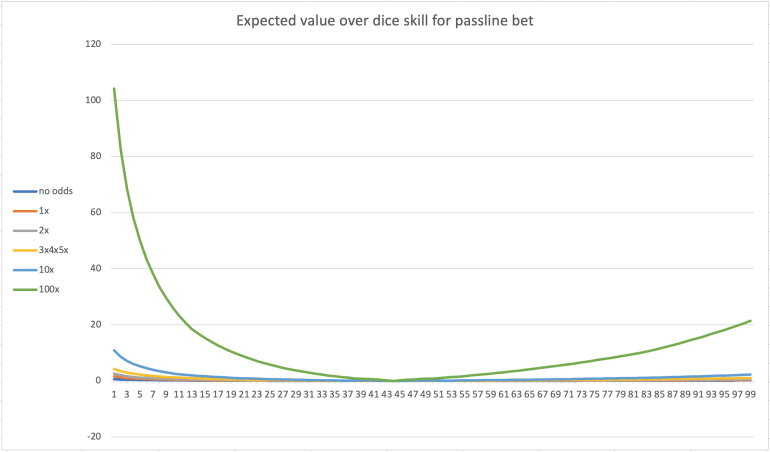
The interesting part, of course, is the range around purely random rolls, which has the skill value of 44:
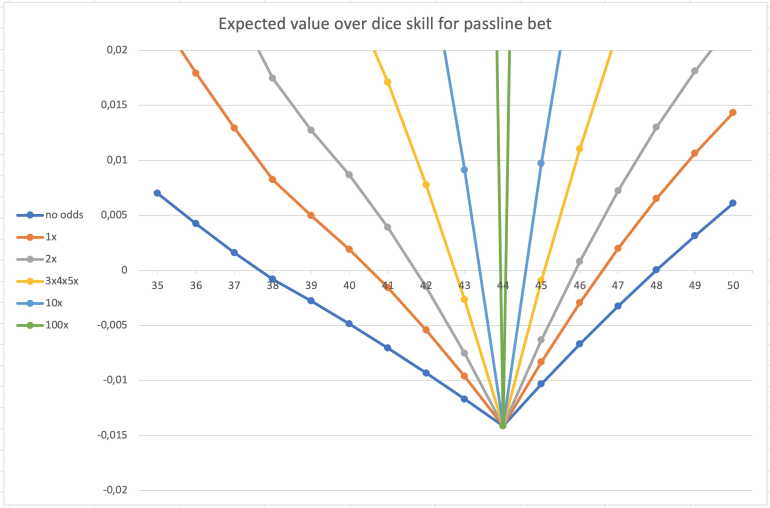
Here the dice settings for those skill levels that break even or are the first having positive expectation:
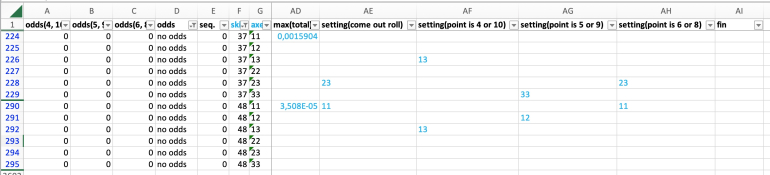
skill 48 - come out: 11; 4 or 10: 13; 5 or 9: 12; 6 or 8: 11
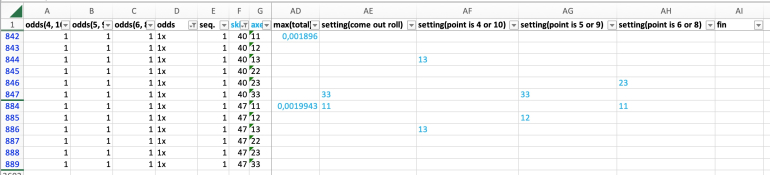
skill 47 - come out: 11; 4 or 10: 13; 5 or 9: 12; 6 or 8: 11
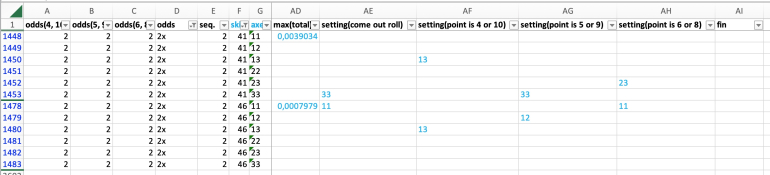
skill 46 - come out: 11; 4 or 10: 13; 5 or 9: 12; 6 or 8: 11
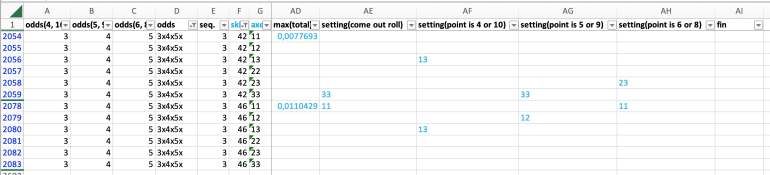
skill 46 - come out: 11; 4 or 10: 13; 5 or 9: 12; 6 or 8: 11
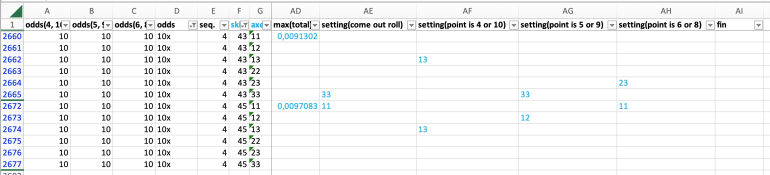
skill 45 - come out: 11; 4 or 10: 13; 5 or 9: 12; 6 or 8: 11
skill 45 - come out: 11; 4 or 10: 13; 5 or 9: 12; 6 or 8: 11
My definition of "on axis" is rather general. It determines the axes after the dice have come to a rest on the table (how the axes may be influenced remains to the shooter ...):
axes 11 - numbers 1 and 6 on both dice are pierced by the imaginary axis
axes 12 - numbers 1 and 6 for one die, numbers 2 and 5 for the other die are pierced by the imaginary axis
axes 13 - numbers 1 and 6 for one die, numbers 3 and 4 for the other die are pierced by the imaginary axis
axes 22 - numbers 2 and 5 on both dice are pierced by the imaginary axis
axes 23 - numbers 2 and 5 for one die, numbers 3 and 4 for the other die are pierced by the imaginary axis
axes 33 - numbers 3 and 4 for both dice are pierced by the imaginary axis
I'm using as the skill level the probability, that the four other sides do not tip over on axis.
For a single die this probability is 4/6.
For two dice the probability is 4/6*4/6 = 16/36 = 4/9.
Expanding 4/9 by 11 yields 44/99, with 44 being the skill level for purely random rolls.
The skill level can therefore range over the 100 values from 0 through 99.
From a given skill level the probabilities of the individual, now biased sides of the die can be calculated backwards:
p(side not on axis) = (sqrt(skill/99))/4
p(side pierced by axis) = (1-sqrt(skill/99))/2
The exhaustive search is not too complicated but is a whole lot of data. Please let me know if you would like to have the formulas. I will try to find a way how to post it.
This set (5 or 9: 33) wouldn't be used for on-axes 5's or 9's.
Pardon my ignorance...
Please explain why 4 out of 9(or 44 out of 99) would indicate the "skill level for purely random rolls" ?
Is there a way to match SRR (rolls before 7) values to any of these"probability" numbers: 1 thru 99 ?
Is there a linear relationship anywhere?
It would appear that a miniscule level of on-axis skill (43 vs. 44) could make large odds-bets more profitable sooner.
That appears to fly in the face of common sense. Is this a case of personal experience vying against the
large sampling of an Excel/computer simulation?
The graph for the "expected value over the full range of skill levels" is highly skewed to the lower values.
Please explain what it means?
Thanks.
Thanks for your questions.
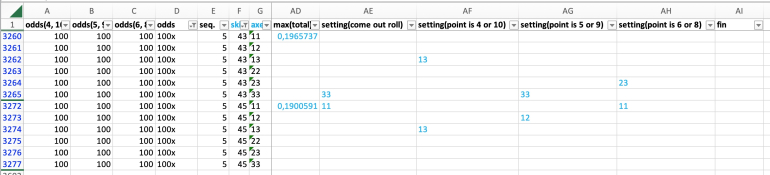
My result is based on comparing the expected value for all six axes under the skill level of 43.Quote: onebok"skill 43 - come out: 33; 4 or 10: 13; 5 or 9: 33; 6 or 8: 23"
This set (5 or 9: 33) wouldn't be used for on-axes 5's or 9's.
Once a point of 5 or 9 is established, the expected value is:
(p(5)/(p(5)+p(7))*(1+(6/4)*odds)+(p(7)/(p(5)+p(7))*(-1-odds)
The components:
p(5) and p(7) are the probabilities for rolling a 5 and rolling a 7.
p(9) is identical (symetrical) to p(5).
(p(5)/(p(5)+p(7)) is the probabilitiy of rolling the point.
(1+(6/4)*odds) is the gain of 1 unit to the initial bet plus 6/4 times the amount to the free odds bet.
(p(7)/(p(5)+p(7)) is the probability of sevening out.
(-1-odds) is the loss of the initial bet and of the free odds bet.
The highest expected values for the given cases are produced by the 33 axes (see bold in coloured sections):
No need to apologize. Your questions are perfect to explain more about the details of the approach.Quote:Pardon my ignorance...
In the case of purely random rolls, the probability of both dice staying on axis and showing any of the other four sides isQuote:Please explain why 4 out of 9(or 44 out of 99) would indicate the "skill level for purely random rolls" ?
p()=(4/6)*(4/6)=16/36=4/9
or
p()=(4/6)*(4/6)=(2/3)*(2/3)=4/9
Any devition of the enumerator from this value of 4 produces probabilities which
either are smaller or greater than 4/9.
p()<4/9 means that the four sides appear less often than they should.
p()>4/9 means that the four sides appear more often than they should.
These biased rolls are the central idea of this approach.
I expanded the 4/9 by 11 to have a range of 100 integer values which can be used to define a player's skill level, i.e. to describe how biased the player's rolls actually are. Shooting the dice 99 times and counting the on-axis tosses, produces a rough first estimate for the player's skill level. Counting the tosses during play can then be used to further monitor the skill level.
My approach is purely based on the mathematical property of expected values of tosses biased by combinations of skill levels and axis settings. The 7 is considered a number as any other of the numbers 2 through 12. The optimal strategy only depends on the maximum expectation, not on certain numbers rolled.Quote:Is there a way to match SRR (rolls before 7) values to any of these"probability" numbers: 1 thru 99 ?
Is there a linear relationship anywhere?
At first glance, I also was surprised when I saw in the results that the free odds bets are a real booster for the expected value. A second thought reveals that this feature neither is wrong nor is illogical:Quote:It would appear that a miniscule level of on-axis skill (43 vs. 44) could make large odds-bets more profitable sooner.
That appears to fly in the face of common sense.
The free odds bets have an expected value of zero - but only for the case of purely random rolls.
The goal is to bias the rolls in such a way that the winning ones appear more often. This not only means that the initial bet will win more often but of course also the free odds bets together with it. The initial bet has to work its way from -0.014 up to zero before it will be able to enter positive expectation. The free odds bets already start from zero. Small improvements, which still keep the initial bet below zero, are a positive contribution of the free odds bets to the overall result, right from the start.
The results produced here are not derived from simulations but are soley based on the equations of expected value.Quote:Is this a case of personal experience vying against the
large sampling of an Excel/computer simulation?
I'm sorry, I don't have an explanation. I'm using the equations of expected value as they are and this is what they look like over the range of parameters.Quote:The graph for the "expected value over the full range of skill levels" is highly skewed to the lower values.
Please explain what it means?
Thanks.
I hope my explanations are comprehensible. Please keep asking, if things remain unclear.
Your odds results look odd because you are probably using some odd definition of expected value that is at odds with the way the odd AP would typically define it.Quote: ThomasK'm sorry, I don't have an explanation. I'm using the equations of expected value as they are and this is what they look like over the range of parameters.
I hope my explanations are comprehensible. Please keep asking, if things remain unclear.
link to original post
Could you please state clearly what your "equations of expected value are? I do not see them defined in your post.
"Here the dice settings for those skill levels that break even or are the first having positive expectation:"
the first line of each pair of "skills" shows "5 or 9: 33" which appears to state that the set used for gaining
an on-axis 5 or 9 rotates around the 3-4 3-4 axes. I assume you abbreviate this to 33 axes.
No on-axis 5's or 9's are possible when dice rotate around the "33" axes.
Only an off-axis die would cause a 5 or 9 when using dice rotating around their 33 axes.
How can your calculated probabilities be most favorable for 5 or 9 when using
this axis for both dice when it should be zero on-axis probability?
The expected value is a weighted sum. The terms of the sum are outcomes multiplied by their repective probabilities.Quote: MentalYour odds results look odd because you are probably using some odd definition of expected value that is at odds with the way the odd AP would typically define it.Quote: ThomasK'm sorry, I don't have an explanation. I'm using the equations of expected value as they are and this is what they look like over the range of parameters.
I hope my explanations are comprehensible. Please keep asking, if things remain unclear.
link to original post
Could you please state clearly what your "equations of expected value are? I do not see them defined in your post.
link to original post
For the passline bet this weighted sum is
probability of craps times minus the initial unit lost
plus probability of frontline winner times 1 unit paid to the initial unit
plus probability of either four or ten estblished, times
probability of four being rolled
times 1 unit paid to the initial unit
plus 6/3 times the free odds bet paid to the free odds bet
plus probability of seven out
times minus 1 unit, the initial unit lost
minus the free odds bet, lost
(remark: probability of four used here, as it is identical / symmetrical to ten)
plus probability of either five or nine established, times
probability of five being rolled
times 1 unit paid to the initial unit
plus 6/4 times the free odds bet paid to the free odds bet
plus probability of seven out
times minus 1 unit, the initial unit lost
minus the free odds bet, lost
(remark: probability of five used here, as it is identical / symmetrical to nine)
plus probability of either six or eight established, times
probability of six being rolled
times 1 unit paid to the initial unit
plus 6/5 times the free odds bet paid to the free odds bet
plus probability of seven out
times minus 1 unit, the initial unit lost
minus the free odds bet, lost
(remark: probability of six used here, as it is identical / symmetrical to eight)
Inserting the values of the random game:
(4/36)*(-1) +
(8/36)*(1) +
(6/36)*( (3/9)*(1+(6/3)*odds) + (6/9)*(-1-odds) ) +
(8/36)*( (4/10)*(1+(6/4)*odds) + (6/10)*(-1-odds) ) +
(10/36)*( (5/11)*(1+(6/5)*odds) + (6/11)*(-1-odds) )
Generalizing the probabilties:
(p(2)+p(3)+p(12))*(-1) +
(p(7)+p(11))*(1) +
(p(4)+p(10)*( ((p(4)/((p(4)+p(7)))*(1+(6/3)*odds) + ((p(7)/((p(4)+p(7)))*(-1-odds) ) + ; p(4) === p(10)
(p(5)+p(9)*( ((p(5)/((p(5)+p(7)))*(1+(6/4)*odds) + ((p(7)/((p(5)+p(7)))*(-1-odds) ) + ; p(5) === p(9)
(p(6)+p(8)*( ((p(6)/((p(6)+p(7)))*(1+(6/5)*odds) + ((p(7)/((p(6)+p(7)))*(-1-odds) ) ; p(6) === p(8)
The idea of my approach is, to vary the probabilities p() in such a way that they represent biased rolls.
This is a great question and a good starting point to explain "axis" and "skill" in more detail.Quote: onebokUnder your paragraph that begins with:
"Here the dice settings for those skill levels that break even or are the first having positive expectation:"
the first line of each pair of "skills" shows "5 or 9: 33" which appears to state that the set used for gaining
an on-axis 5 or 9 rotates around the 3-4 3-4 axes. I assume you abbreviate this to 33 axes.
No on-axis 5's or 9's are possible when dice rotate around the "33" axes.
Only an off-axis die would cause a 5 or 9 when using dice rotating around their 33 axes.
How can your calculated probabilities be most favorable for 5 or 9 when using
this axis for both dice when it should be zero on-axis probability?
link to original post
The "axis", here 33, is what the player aims for. He tries to achieve the dice coming to a rest with 3 and 4 on the sides on both dice. But the trials are random and only with a probability of 4/9 he will be able to do so. With a probability of 5/9 any one die or even both dice will tip over and 3s or 4s will show on top of any die. In these cases the player will be able to roll a 5 or a 9, although he wanted to stay on axis. This is the case of purely random rolls, i.e. a skill level of 44.
Any skill level below 44, here 37, means that the player is not even able to keep the dice on axis as often as a random roller would. The player's dice tip over more often, giving him more opportunities to roll a 5 or a 9. The probability of keeping both dice on axis is only 37/99 < 4/9 (=44/99).
On the other hand, in the next line below the one you're referring to, you can see that the player uses the 12 setting for 5s and 9s. In this case the player has a skill level of 48, which is greater than 44, and which indicates that the player is able to keep the dice on axis more often than a random roller would. Thus the player has more opportunities to roll a 5 or a 9. The probability of keeping both dice on axis here is 48/99 > 4/9 (=44/99).
As I suspected, you are calculating absolute expected value in terms of bet units for the initial pass line bet. You are not expressing EV in terms of a percentage of money wagered. When you are able to tilt the probabilities, the absolute EV gets very large as you increase the odds ratio.Quote: ThomasKThe expected value is a weighted sum. The terms of the sum are outcomes multiplied by their repective probabilities.Quote: MentalYour odds results look odd because you are probably using some odd definition of expected value that is at odds with the way the odd AP would typically define it.Quote: ThomasK'm sorry, I don't have an explanation. I'm using the equations of expected value as they are and this is what they look like over the range of parameters.
I hope my explanations are comprehensible. Please keep asking, if things remain unclear.
link to original post
Could you please state clearly what your "equations of expected value are? I do not see them defined in your post.
link to original post
For the passline bet this weighted sum isprobability of craps times minus the initial unit lost
plus probability of frontline winner times 1 unit paid to the initial unit
plus probability of either four or ten estblished, times
probability of four being rolled
times 1 unit paid to the initial unit
plus 6/3 times the free odds bet paid to the free odds bet
plus probability of seven out
times minus 1 unit, the initial unit lost
minus the free odds bet, lost
(remark: probability of four used here, as it is identical / symmetrical to ten)
plus probability of either five or nine established, times
probability of five being rolled
times 1 unit paid to the initial unit
plus 6/4 times the free odds bet paid to the free odds bet
plus probability of seven out
times minus 1 unit, the initial unit lost
minus the free odds bet, lost
(remark: probability of five used here, as it is identical / symmetrical to nine)
plus probability of either six or eight established, times
probability of six being rolled
times 1 unit paid to the initial unit
plus 6/5 times the free odds bet paid to the free odds bet
plus probability of seven out
times minus 1 unit, the initial unit lost
minus the free odds bet, lost
(remark: probability of six used here, as it is identical / symmetrical to eight)
Inserting the values of the random game:(4/36)*(-1) +
(8/36)*(1) +
(6/36)*( (3/9)*(1+(6/3)*odds) + (6/9)*(-1-odds) ) +
(8/36)*( (4/10)*(1+(6/4)*odds) + (6/10)*(-1-odds) ) +
(10/36)*( (5/11)*(1+(6/5)*odds) + (6/11)*(-1-odds) )
Generalizing the probabilties:(p(2)+p(3)+p(12))*(-1) +
(p(7)+p(11))*(1) +
(p(4)+p(10)*( ((p(4)/((p(4)+p(7)))*(1+(6/3)*odds) + ((p(7)/((p(4)+p(7)))*(-1-odds) ) + ; p(4) === p(10)
(p(5)+p(9)*( ((p(5)/((p(5)+p(7)))*(1+(6/4)*odds) + ((p(7)/((p(5)+p(7)))*(-1-odds) ) + ; p(5) === p(9)
(p(6)+p(8)*( ((p(6)/((p(6)+p(7)))*(1+(6/5)*odds) + ((p(7)/((p(6)+p(7)))*(-1-odds) ) ; p(6) === p(8)
The idea of my approach is, to vary the probabilities p() in such a way that they represent biased rolls.
link to original post
Maybe it is just me, but I always think in terms of expected win/loss divided by money actually wagered. Then, the EV is around -0.25% for 3/4/5x odd and it is about -0.01% for 100x odds. Your choice to use absolute EV is fine, but the graphs would be more informative expressed as relative EV.
The expected value is defined as the weighted sum of outcomes and respective probabilities. Normalizing this value by the amout wagered is then called the house edge. As you might recall, the discussion about this is still open. Please see "Schroedinger's craps (pun intended)" for the question which wager to use as the denominator:Quote: MentalAs I suspected, you are calculating absolute expected value in terms of bet units for the initial pass line bet. You are not expressing EV in terms of a percentage of money wagered. When you are able to tilt the probabilities, the absolute EV gets very large as you increase the odds ratio.Quote: ThomasKThe expected value is a weighted sum. The terms of the sum are outcomes multiplied by their repective probabilities.Quote: MentalYour odds results look odd because you are probably using some odd definition of expected value that is at odds with the way the odd AP would typically define it.Quote: ThomasK'm sorry, I don't have an explanation. I'm using the equations of expected value as they are and this is what they look like over the range of parameters.
I hope my explanations are comprehensible. Please keep asking, if things remain unclear.
link to original post
Could you please state clearly what your "equations of expected value are? I do not see them defined in your post.
link to original post
For the passline bet this weighted sum isprobability of craps times minus the initial unit lost
plus probability of frontline winner times 1 unit paid to the initial unit
plus probability of either four or ten estblished, times
probability of four being rolled
times 1 unit paid to the initial unit
plus 6/3 times the free odds bet paid to the free odds bet
plus probability of seven out
times minus 1 unit, the initial unit lost
minus the free odds bet, lost
(remark: probability of four used here, as it is identical / symmetrical to ten)
plus probability of either five or nine established, times
probability of five being rolled
times 1 unit paid to the initial unit
plus 6/4 times the free odds bet paid to the free odds bet
plus probability of seven out
times minus 1 unit, the initial unit lost
minus the free odds bet, lost
(remark: probability of five used here, as it is identical / symmetrical to nine)
plus probability of either six or eight established, times
probability of six being rolled
times 1 unit paid to the initial unit
plus 6/5 times the free odds bet paid to the free odds bet
plus probability of seven out
times minus 1 unit, the initial unit lost
minus the free odds bet, lost
(remark: probability of six used here, as it is identical / symmetrical to eight)
Inserting the values of the random game:(4/36)*(-1) +
(8/36)*(1) +
(6/36)*( (3/9)*(1+(6/3)*odds) + (6/9)*(-1-odds) ) +
(8/36)*( (4/10)*(1+(6/4)*odds) + (6/10)*(-1-odds) ) +
(10/36)*( (5/11)*(1+(6/5)*odds) + (6/11)*(-1-odds) )
Generalizing the probabilties:(p(2)+p(3)+p(12))*(-1) +
(p(7)+p(11))*(1) +
(p(4)+p(10)*( ((p(4)/((p(4)+p(7)))*(1+(6/3)*odds) + ((p(7)/((p(4)+p(7)))*(-1-odds) ) + ; p(4) === p(10)
(p(5)+p(9)*( ((p(5)/((p(5)+p(7)))*(1+(6/4)*odds) + ((p(7)/((p(5)+p(7)))*(-1-odds) ) + ; p(5) === p(9)
(p(6)+p(8)*( ((p(6)/((p(6)+p(7)))*(1+(6/5)*odds) + ((p(7)/((p(6)+p(7)))*(-1-odds) ) ; p(6) === p(8)
The idea of my approach is, to vary the probabilities p() in such a way that they represent biased rolls.
link to original post
Maybe it is just me, but I always think in terms of expected win/loss divided by money actually wagered. Then, the EV is around -0.25% for 3/4/5x odd and it is about -0.01% for 100x odds. Your choice to use absolute EV is fine, but the graphs would be more informative expressed as relative EV.
link to original post
- the (a priori) maximum wager, which is needed to play a 6 or an 8 with full odds,
- the(a posteriori) average calculated from the probabilities and amounts of the four possible branches "craps or frontline winner", "point is 4 or 10", "point is 5 or 9", and "point is 6 or 8", or
- the initial bet only, because in the purely random game the free odds bets have an expected value of zero. (In the case of biased rolls this no longer is valid, though.)
And the question to be answered is, whether biased rolls are able to overcome the negative expectation after all and how much it would take to do so.


