Quote: heatmaptbh i have no clue how dice setting even began.
the technology to "deal" with dice setting or literally anything to do with dice cheating has been dealt with from a "table game security" prospective since the 50s
link to original post
Every single game has been equally as well.
Quote: unJonI find the evidence that the casinos have taken defensive measures to be persuasive. Hit back wall. Add diamond bumps to back wall. Add some sponginess under felt.
The casinos must have felt that some level of dice influence worked for some people without those countermeasures. To me, the open question is whether thereís a level of successful dice influence possible given the current set of countermeasures.
And someday the casinos might add another rule if they thing there is. Add bumps to felt near walls. Etc.
link to original post
Binion's once told me that the dice had to hit the back wall, "In the air," which is pretty funny. I was setting the dice, of course, but I have no idea how to make that actually impact anything...I just like the optic in the rare event I play Craps.
Last I heard, he was back to playing blackjack and video poker.
Itís amazing that an educated person would believe in something like thisÖand then pay some scam artist a few hundred bucks per session
Quote: billryanIt was quite the rage on Long Island a bit earlier. There was a whole cottage industry involving setting up craps tables in mancaves and having dice control seminars. They were male tupperware parties.
link to original post
So they spent quite a BIT of COIN on that! :)
Atlantic City 2009
http://content.time.com/time/nation/article/0,8599,1901663,00.html
A lucky shooter will have much more success than a dice setter ever willQuote: Marcusclark66So I would assume grandma rolling the dice 154 rolls continuously, mastered the art of dice setting?
Atlantic City 2009
http://content.time.com/time/nation/article/0,8599,1901663,00.html
link to original post
Quote: Ace2A lucky shooter will have much more success than a dice setter ever willQuote: Marcusclark66So I would assume grandma rolling the dice 154 rolls continuously, mastered the art of dice setting?
Atlantic City 2009
http://content.time.com/time/nation/article/0,8599,1901663,00.html
link to original post
link to original post
Thank you. I see it every day/night in one firm or another. Although not world records, I see such things people would challenge as even being factual.
Earlier today a person loses well over $10,000.00 of his own cash. Returns with $40.00 and works it up to right around $30,000.00 or so. Colors up and then returns again. Within two hours gives it all back. Everyone saying he should have left with the $30k.
Quote: Marcusclark66Seriously people do believe that they can throw the dice across the entire table, have them hit the backstop and they can set the dice?
I can understand if they allowed shooters to slide the dice across the whole table thatís one thing, but that would be an invalid attempt at a roll.
How does a casino player actually throw the dice across the entire table, hit the backstop and land on the preset number totally blows my mind. Somebody explain to me what the thought process is, that actually works in the players favor.
link to original post
You have 100% misunderstanding about what dice setting and dice influencing is supposed to be.
First, you dont stand at the end of the table. You stand closest to the stick.
You do not Chuck the dice. You gently toss them.
Third, you try to keep the dice parallel to the table and close to each other with as light (soft) a bounce as possible to the lowest point on the back wall. Ideally your dice come to rest under the first row of Pyramids.
Quote: ChumpChangeJust roll 7's on the Come-outs and figure out why you can't make your point for 20+ rolls.
link to original post
Give me a turn like that -- 20 rolls-- and I'd make a fortune.
And, after all that dice influencing, you will still roll a seven exactly 1 of every 6 rolls (on average)Quote: AlanMendelsonQuote: Marcusclark66Seriously people do believe that they can throw the dice across the entire table, have them hit the backstop and they can set the dice?
I can understand if they allowed shooters to slide the dice across the whole table thatís one thing, but that would be an invalid attempt at a roll.
How does a casino player actually throw the dice across the entire table, hit the backstop and land on the preset number totally blows my mind. Somebody explain to me what the thought process is, that actually works in the players favor.
link to original post
You have 100% misunderstanding about what dice setting and dice influencing is supposed to be.
First, you dont stand at the end of the table. You stand closest to the stick.
You do not Chuck the dice. You gently toss them.
Third, you try to keep the dice parallel to the table and close to each other with as light (soft) a bounce as possible to the lowest point on the back wall. Ideally your dice come to rest under the first row of Pyramids.
link to original post
Quote: ChumpChangeI laid the 9 for 20+ rolls and only won that one bet.
link to original post
A lay bet only wins once.
What rolled the other 19 times?
Quote: Ace2And, after all that dice influencing, you will still roll a seven exactly 1 of every 6 rolls (on average)Quote: AlanMendelsonQuote: Marcusclark66Seriously people do believe that they can throw the dice across the entire table, have them hit the backstop and they can set the dice?
I can understand if they allowed shooters to slide the dice across the whole table thatís one thing, but that would be an invalid attempt at a roll.
How does a casino player actually throw the dice across the entire table, hit the backstop and land on the preset number totally blows my mind. Somebody explain to me what the thought process is, that actually works in the players favor.
link to original post
You have 100% misunderstanding about what dice setting and dice influencing is supposed to be.
First, you dont stand at the end of the table. You stand closest to the stick.
You do not Chuck the dice. You gently toss them.
Third, you try to keep the dice parallel to the table and close to each other with as light (soft) a bounce as possible to the lowest point on the back wall. Ideally your dice come to rest under the first row of Pyramids.
link to original post
link to original post
You can also win by calling off your bets before the 7 rolls.
link to original post
Wow. So now you're telling me dice can count?
Let me wrap it up this way.
There are skilled gamblers.
Some skills involve counting cards.
Some skills involve reading other players.
Some skills involve palming chips or cards.
Some skills involve handling dice.
Some pitchers can throw knuckle balls and some cant
My guess is that, if influencing the dice is possible at all, it is extremely difficult. I mean getting a season batting average of .400 in Major League Baseball difficult. So, if you really want to be a craps advantage player by that route, first of all, you need your own craps table. Not the silly little "practice rigs" that many of the dice setting "experts" suggest. You need a full size craps table, with dice and all, just as close to what is in the casino as possible. Then, practice practice practice, and log your results. If, after tens, if not hundreds of thousands of rolls, you get statistically meaningful results, then maybe you are ready to try to make real money playing craps, at least until the casino backs you off. I think there are more profitable ways to spend that time, even in the context of casino advantage play.
Will I keep setting the dice? Probably, but the reality is that it will be just about as effective as wearing my lucky hat.
Better yet, bet a million dollars on Come right before the seven rolls. Easy moneyQuote: AlanMendelson
You can also win by calling off your bets before the 7 rolls.
link to original post
Basic math/statistics show that, over the long term, exactly 1/6th of your rolls will be a 7. Just like 1/2 of coin flips will be heads over the long term. Basic math is not up for debate.Quote: AlanMendelson"And, after all that dice influencing, you will still roll a seven exactly 1 of every 6 rolls (on average)"
link to original post
Wow. So now you're telling me dice can count?
Let me wrap it up this way.
There are skilled gamblers.
Some skills involve counting cards.
Some skills involve reading other players.
Some skills involve palming chips or cards.
Some skills involve handling dice.
Some pitchers can throw knuckle balls and some cant
link to original post
Dice setting is up for debate. Letís see one example of someone consistently demonstrating dice controlÖcall it 4+ deviations from expectations. Weíll be waiting patiently
Does math say that after 600 rolls, 100 of them will be 7? Or after six million rolls, exactly one million will be 7s? Not 999,997 but always 1,000,000?
I'd say that if I rolled six million times, the chances of rolling exactly one million sevens are fairly low.
Perhaps the proper wording is: With sufficient rolls you will be 99.999999999999999% confident of getting between 1/6.0000000000001 sevens and 1/5.99999999999 sevens. Which, for all practical purposes, is a 100% chance of getting 1/6 sevens. Does that version work for you ?Quote: billryanDoes basic math really say that?
Does math say that after 600 rolls, 100 of them will be 7? Or after six million rolls, exactly one million will be 7s? Not 999,997 but always 1,000,000?
I'd say that if I rolled six million times, the chances of rolling exactly one million sevens are fairly low.
link to original post
I say if you had 100 people each throw 6,000,000 rolls, the chances of two of them having exactly 1,000,000 sevens is slim.
The overall average number will be very close to that 1,000,000 but chances are no one lands on it exactly. That is my problem with using the word.
The average MLB outfielder hits .271, with 26 homeruns and 91 RBI. There are 160plus MLB outfielders. What are the chances you will find one that hit exactly .271 with 26 HRs and 91 RBIs?
Quote: Ace2Perhaps the proper wording is: With sufficient rolls you will be 99.999999999999999% confident of getting between 1/6.0000000000001 sevens and 1/5.99999999999 sevens. Which, for all practical purposes, is a 100% chance of getting 1/6 sevens. Does that version work for you ?Quote: billryanDoes basic math really say that?
Does math say that after 600 rolls, 100 of them will be 7? Or after six million rolls, exactly one million will be 7s? Not 999,997 but always 1,000,000?
I'd say that if I rolled six million times, the chances of rolling exactly one million sevens are fairly low.
link to original post
link to original post
This all assumes no physics involved in trying to influence the dice.
You are mixing up percentages and absolute numbers. I think thatís the main source of your confusion. We are looking at the ratio of sevens to total rolls, not the number of sevensQuote: billryanNot really. Would ou stake your life that you'd get 1,000,000 sevens after 6,000,000 rolls? I don't think you can say you will get exactly/1/6th sevens and then say you'll get a range between A and B which means 100%.
I say if you had 100 people each throw 6,000,000 rolls, the chances of two of them having exactly 1,000,000 sevens is slim.
The overall average number will be very close to that 1,000,000 but chances are no one lands on it exactly. That is my problem with using the word.
The average MLB outfielder hits .271, with 26 homeruns and 91 RBI. There are 160plus MLB outfielders. What are the chances you will find one that hit exactly .271 with 26 HRs and 91 RBIs?
link to original post
Quote: Ace2You are mixing up percentages and absolute numbers. I think thatís the main source of your confusion. We are looking at the ratio of sevens to total rolls, not the number of sevensQuote: billryanNot really. Would ou stake your life that you'd get 1,000,000 sevens after 6,000,000 rolls? I don't think you can say you will get exactly/1/6th sevens and then say you'll get a range between A and B which means 100%.
I say if you had 100 people each throw 6,000,000 rolls, the chances of two of them having exactly 1,000,000 sevens is slim.
The overall average number will be very close to that 1,000,000 but chances are no one lands on it exactly. That is my problem with using the word.
The average MLB outfielder hits .271, with 26 homeruns and 91 RBI. There are 160plus MLB outfielders. What are the chances you will find one that hit exactly .271 with 26 HRs and 91 RBIs?
link to original post
link to original post
I think rephrasing billryanís question: after 6,000,000 tosses, what is the range of numbers of 7 that you would bet your life that you would be between.
Basic math/statistics show that, over the long term, exactly 1/6th of your rolls will be a 7. Just like 1/2 of coin flips will be heads over the long term. Basic math is not up for debate.
I disagree with your use of exactly. If you said on average, we would have no issue, but you say "exactly". I say the chances of you have exactly a million sevens after exactly six million rolls is slim. Just as having 500,000 heads in 1,000,000 coin tosses is very slim. If a million people toss a million coins, how many of them will have exactly 500,000? The million folks may average 500,000 but very few will hit that exact market.
Quote: Ace2You are mixing up percentages and absolute numbers. I think thatís the main source of your confusion. We are looking at the ratio of sevens to total rolls, not the number of sevens
link to original post
Quote: billryanThese are your exact words:
Basic math/statistics show that, over the long term, exactly 1/6th of your rolls will be a 7. Just like 1/2 of coin flips will be heads over the long term. Basic math is not up for debate.
I disagree with your use of exactly. If you said on average, we would have no issue, but you say "exactly". I say the chances of you have exactly a million sevens after exactly six million rolls is slim. Just as having 500,000 heads in 1,000,000 coin tosses is very slim. If a million people toss a million coins, how many of them will have exactly 500,000? The million folks may average 500,000 but very few will hit that exact market.
link to original post
Excel breaks for me after 1,022 coin flips, but for that case it get that about 2.5% of people have exactly 511 heads after 1,022 coin flips.
This can be closely approximated by 1 / (1022 * .5 * π)^.5 = 2.496%. Itís derived from Sterlingís approximationQuote: unJon
Excel breaks for me after 1,022 coin flips, but for that case it get that about 2.5% of people have exactly 511 heads after 1,022 coin flips.
link to original post
Quote: billryanThe average MLB outfielder hits .271, with 26 homeruns and 91 RBI. There are 160plus MLB outfielders. What are the chances you will find one that hit exactly .271 with 26 HRs and 91 RBIs?
link to original post
Carlos Correa hit .279 with 26 HRs and 92 RBIs. Pretty dang close!
Then again, he's a shortstop!
Thus, 95% of the outcomes for the number of 7s would be in the range 998,000 to 1,002,000 if its normally distributed.
But I've always questioned whether this kind of data is normally distributed. A total of 7 is one of eleven different possible outcomes that must occur, and the sum of the frequencies of the 11 outcomes must sum to the total number of trials, in this example they must sum to 6 million. Since the system is not binary (heads or tails) I think that the frequency of the eleven possible outcomes cannot all be normally distributed. Their statistical deviations cannot be entirely independent.
I'm all ears if anyone can explain to me the frequency distribution of expected outcomes when there are more than 2 possible outcomes. I just am weak in this area of statistics.
This is still a binary event since there are only two possible outcomes: you roll a seven or you donít.Quote: gordonm888After 6 million crap tosses, the average number of 7s you would be expected to toss are 1 million, but there will be a frequency distribution of outcomes for numbers close to 1,000,000. If this were normally distributed you would say the expected value of 7s is one million but the frequency distribution has a standard deviation of 1,000.
Thus, 95% of the outcomes for the number of 7s would be in the range 998,000 to 1,002,000 if its normally distributed.
But I've always questioned whether this kind of data is normally distributed. A total of 7 is one of eleven different possible outcomes that must occur, and the sum of the frequencies of the 11 outcomes must sum to the total number of trials, in this example they must sum to 6 million. Since the system is not binary (heads or tails) I think that the frequency of the eleven possible outcomes cannot all be normally distributed. Their statistical deviations cannot be entirely independent.
I'm all ears if anyone can explain to me the frequency distribution of expected outcomes when there are more than 2 possible outcomes. I just am weak in this area of statistics.
link to original post
If you rolled 6,000,000 times, the SD is (1/6 * 5/6 * 6000000)^.5 =~ 913. So you could be about 95% confident of rolling 1,000,000 sevens +/- 913.
This distribution will be very close to symmetrical within any useful range (like 5 or even 10 SDs). But itís not a perfectly symmetric distribution like a coin flip when each flip has a 50% success rate. Even the normal distribution is just an estimate of the binomial one, though a very accurate estimate for large n.
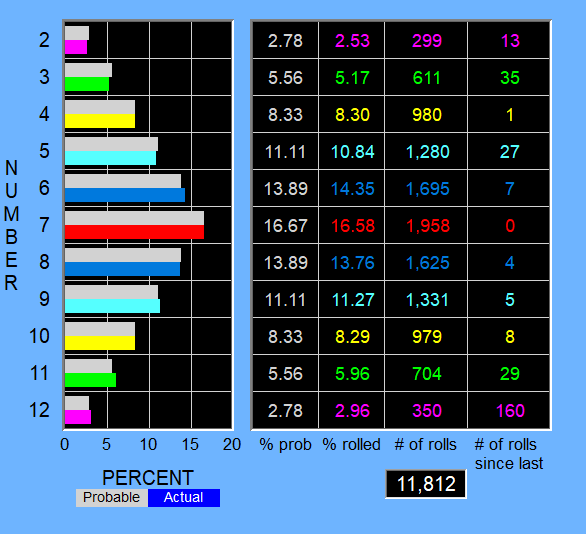
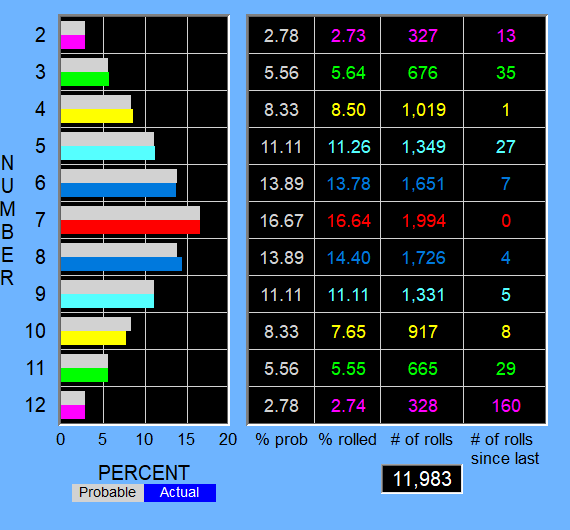
I've got two players up in WinCraps. There's a total of 23,795 rolls in the statistics (11,812 + 11,983 = 23,795), so one player rolls, then the other player rolls. The other player may not be betting anything, but apparently they are rolling the dice. In fact Player 2 hasn't made a bet yet.
Player 1 has made 20,456 wagers, won 9,380 of them and lost 11,076 bets for a net loss of 1,696 bets or -8.291%.
Player 1 is up $24K or 1.065% though. Big wagers can catch me up.
You can see in the 2nd column in the charts how far actual number % of rolls varied from expected % number of rolls in the first column. There could be up to a 1%+ difference, but most of the time it's a sub- 0.20% difference.
Both players rolled a nine 1,331 times but the percentage is different because they rolled a different amount of total times but had an equal number of times being a shooter.
If you have 16.58% of 6 million rolls land on a 7, that'd be 994,800, or 5,200 short.
If you have 16.64% of 6 million rolls land on a 7, that'd be 998,400, or 1,600 short.
If you have 16.00% of 6 million rolls land on a 7, that'd be 960,000, or 40,000 short.
If you have 17.67% of 6 million rolls land on a 7, that'd be 1,060,200, or 60,200 extra.
Quote: unJonQuote: billryanThese are your exact words:
Basic math/statistics show that, over the long term, exactly 1/6th of your rolls will be a 7. Just like 1/2 of coin flips will be heads over the long term. Basic math is not up for debate.
I disagree with your use of exactly. If you said on average, we would have no issue, but you say "exactly". I say the chances of you have exactly a million sevens after exactly six million rolls is slim. Just as having 500,000 heads in 1,000,000 coin tosses is very slim. If a million people toss a million coins, how many of them will have exactly 500,000? The million folks may average 500,000 but very few will hit that exact market.
link to original post
Excel breaks for me after 1,022 coin flips, but for that case it get that about 2.5% of people have exactly 511 heads after 1,022 coin flips.
link to original post
I have an exact fraction, but it's a 300,000-or-so digit integer divided by 2^999,993, so it won't fit. However, it's "about" 1 / 1253.31445.
Quote: odiousgambitthis is when I think Tuttigym might be right
link to original post
Debating 4th grade arithmetic to such absurd levels is truly buffoonery. Pissing contest, anyone? Cannot wait for the next one. Thanks OG.
tuttigym


