Thread Rating:
May 31st, 2015 at 2:44:35 PM
permalink
Taking the play: 6/8 $6 each
The probability of losing 4 times in a row we know is (6/16)^4.
That will happen 1 in 50.5679 trials.
How do you find calculate which trial # you are most probable to lose on?
Thanks
The probability of losing 4 times in a row we know is (6/16)^4.
That will happen 1 in 50.5679 trials.
How do you find calculate which trial # you are most probable to lose on?
Thanks
May 31st, 2015 at 3:02:02 PM
permalink
The first one is most likely to be the first trial to fail. Imagine you're flipping a coin:
Trial 1: 0.50
Trial 2: (1 - trial_1_prob) * 0.50
Trial 3: (1 - trial_2_prob) * 0.50
Trial 4: (1 - trial_3_prob) * 0.50
EDIT: You have to subtract the sum of previous trials from 1.
ie:
Trial 3: (1 - trial_2_prob - trial_1_prob) * 0.5
This is what I got:
Trial 1: 0.50
Trial 2: (1 - trial_1_prob) * 0.50
Trial 3: (1 - trial_2_prob) * 0.50
Trial 4: (1 - trial_3_prob) * 0.50
EDIT: You have to subtract the sum of previous trials from 1.
ie:
Trial 3: (1 - trial_2_prob - trial_1_prob) * 0.5
This is what I got:
Trial | Prob Fail First
1 0.375
2 0.234375
3 0.146484375
4 0.09155273438
5 0.05722045898
6 0.03576278687
7 0.02235174179
8 0.01396983862
9 0.008731149137
10 0.005456968211
11 0.003410605132
12 0.002131628207
13 0.00133226763
14 0.0008326672685
15 0.0005204170428
16 0.0003252606517
17 0.0002032879073
18 0.0001270549421
19 0.00007940933881
20 0.00004963083675
21 0.00003101927297
22 0.00001938704561
23 0.0000121169035
24 0.00000757306469
25 0.000004733165431
26 0.000002958228395
27 0.000001848892747
28 0.000001155557967
29 0.0000007222237292
30 0.0000004513898307
May 31st, 2015 at 8:39:57 PM
permalink
Ah, you have a system you B working on i guessQuote: bahdbwoyTaking the play: 6/8 $6 each
The probability of losing 4 times in a row we know is (6/16)^4.
and that is just for the very next rolls that are from this set {6,7,8}
no other numbers are counted.
WARNING!
OP could be in danger of mixing apples and oranges!
WARNING
WARNING
Ohhhhhh
and each trial is not one roll in length from the set of rolls to count {6,7,8}Quote: bahdbwoyThat will happen 1 in 50.5679 trials.
WARNING
WARNING
Ohhhhhh
each trial is on average
1.568359375
(avg Trial len) 1 + p + p^2 + p^3 where p = 6/16
and 50.5679 * 1.568359375 =
1 in 79.3086 rolls from the set {6,7,8}
of course, if we wants the number of total rolls
we multiply that last value by 36/16 to gets the average number of rolls to get 4 7s in a row: 178.4444444
say 179
that is just the average and not the probability
unique questionQuote: bahdbwoyHow do you find calculate which trial # you are most probable to lose on? Thanks
you mean lose on 4 in a row?
now, "How do you find calculate which..."
well
the heartbeat of the game of Craps IS the roll
so I stay with the roll and not the trial for an event that does NOT count all rolls.
OK,
so i set up a simple recursion in Excel with the "blablabla" (Maria Mayrinck)
prob of a 7 = 6/36
prob of a 6or8 = 10/36
and this starts the 7 streak all over again
and 20/36 = the prob of NO 6,7 or 8 and does not break the 7 streak (you do not lose)
in other words we stay in the state that is equal to the number of 7s in a row
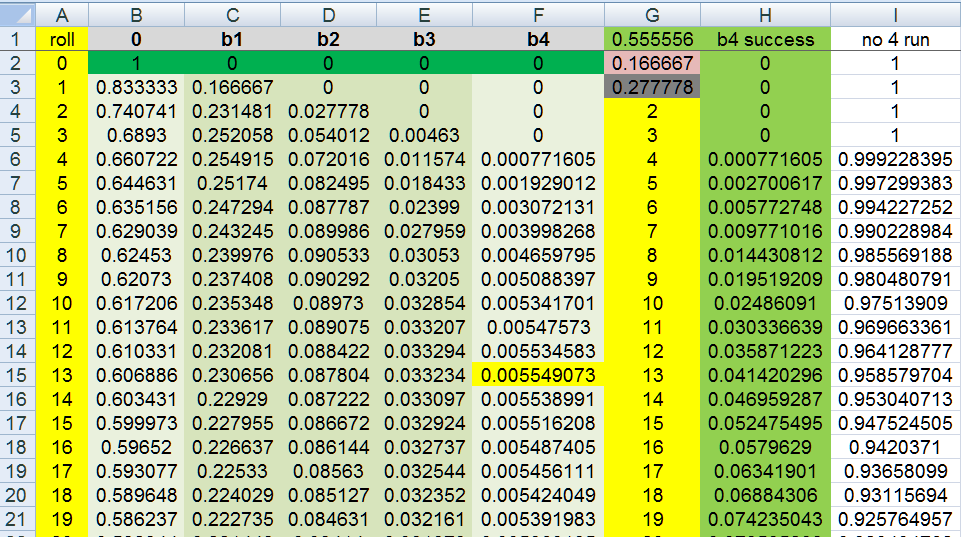
i get roll #13 has the highest single roll probability of being that 4th 7 in a row
it is of course a very small value i do see
but it is what you asked, i thinks... by my translation
other values
first quartile: 56 rolls
median: 126 rolls
third quartile: 245 rolls
Oh, the chance that the 4 in a row 7s do NOT happen in the first 179 rolls = 36.5657909%
i thinks you wants to ask something else, different?
Sally
I Heart Vi Hart
June 1st, 2015 at 1:59:44 AM
permalink
Hi Sally... And thanks.
Just something i wanted to understand. I stumbled back on that old steen/ahigh thread about the HE on this play from a search. Then thought of your mostly likely roll to 7 out thread and wondered.
Not my system of choice though :)
I was asking the most probable attempt # not individual roll (6/7/8) # which i think is what you have or I misunderstood. Could be like you said-- heartbeat is rolls so 13th roll (6/7/8) is more meaningful and yet not so meaningful.
And thats ok if thats the answer.
13 shows of 6/7/8s below but 7 trials
Trial 1: (disregards none 6/7/8) -- 6
Trial 2 : 7,6
Trial 3 : 7,7,7,8
Trial 4: 8
Trial 5 : 7,7,6
Trial 6 : 6
Trial 7: 8
Ect
....
Trial 29: 7,7,7,7
I was getting between 20-30 manually which would seem reasonable. Did have 1 go 62 trials and 1 bust at the 11th attempt. Granted small sample size.
I can rig further with chipstacks i guess :)
Just something i wanted to understand. I stumbled back on that old steen/ahigh thread about the HE on this play from a search. Then thought of your mostly likely roll to 7 out thread and wondered.
Not my system of choice though :)
I was asking the most probable attempt # not individual roll (6/7/8) # which i think is what you have or I misunderstood. Could be like you said-- heartbeat is rolls so 13th roll (6/7/8) is more meaningful and yet not so meaningful.
And thats ok if thats the answer.
13 shows of 6/7/8s below but 7 trials
Trial 1: (disregards none 6/7/8) -- 6
Trial 2 : 7,6
Trial 3 : 7,7,7,8
Trial 4: 8
Trial 5 : 7,7,6
Trial 6 : 6
Trial 7: 8
Ect
....
Trial 29: 7,7,7,7
I was getting between 20-30 manually which would seem reasonable. Did have 1 go 62 trials and 1 bust at the 11th attempt. Granted small sample size.
I can rig further with chipstacks i guess :)
June 1st, 2015 at 7:11:16 AM
permalink
and you should find with a larger sample size that aboutsQuote: bahdbwoyI was getting between 20-30 manually which would seem reasonable. Did have 1 go 62 trials and 1 bust at the 11th attempt. Granted small sample size.
I can rig further with chipstacks i guess :)
50.2954601% of the 7,7,7,7 events will occur by the 35th trial (including trial 35)
this is called the median (for the wait time)
(same concept as the wait time for one 7 to roll.
The prob at each step = 1/6 but the median wait time = 4 rolls)
ok
well then for trials, the most probable attempt is the 1st as mentioned B4
that is simply p = (6/16)^4 (the event of 4 7s in a row B4 a 6or8)
to not be the 1st but the second = q*p (q=1-p)
the 3rd: q^2 * p (fail,fail,success)
and so on
one still gets the average of 1 / (6/16)^4
here is the probs for the 1st 200 attempts
attempt prob on X
1 0.019775391
2 0.019384325
3 0.019000992
4 0.01862524
5 0.018256919
6 0.017895881
7 0.017541983
8 0.017195083
9 0.016855044
10 0.016521729
11 0.016195005
12 0.015874742
13 0.015560813
14 0.015253092
15 0.014951456
16 0.014655785
17 0.014365961
18 0.014081869
19 0.013803395
20 0.013530427
21 0.013262858
22 0.013000579
23 0.012743488
24 0.01249148
25 0.012244456
26 0.012002318
27 0.011764967
28 0.01153231
29 0.011304254
30 0.011080708
31 0.010861583
32 0.010646791
33 0.010436246
34 0.010229866
35 0.010027566
36 0.009829267
37 0.009634889
38 0.009444356
39 0.00925759
40 0.009074517
41 0.008895065
42 0.008719162
43 0.008546737
44 0.008377722
45 0.008212049
46 0.008049653
47 0.007890468
48 0.007734431
49 0.007581479
50 0.007431553
51 0.007284591
52 0.007140535
53 0.006999328
54 0.006860914
55 0.006725236
56 0.006592242
57 0.006461878
58 0.006334092
59 0.006208833
60 0.006086051
61 0.005965697
62 0.005847723
63 0.005732082
64 0.005618728
65 0.005507615
66 0.0053987
67 0.005291938
68 0.005187288
69 0.005084708
70 0.004984156
71 0.004885592
72 0.004788977
73 0.004694274
74 0.004601442
75 0.004510447
76 0.004421251
77 0.004333819
78 0.004248116
79 0.004164108
80 0.004081761
81 0.004001043
82 0.003921921
83 0.003844363
84 0.003768339
85 0.003693819
86 0.003620772
87 0.00354917
88 0.003478984
89 0.003410186
90 0.003342748
91 0.003276644
92 0.003211847
93 0.003148331
94 0.003086072
95 0.003025044
96 0.002965222
97 0.002906584
98 0.002849105
99 0.002792763
100 0.002737535
101 0.002683399
102 0.002630334
103 0.002578318
104 0.002527331
105 0.002477352
106 0.002428361
107 0.002380339
108 0.002333267
109 0.002287126
110 0.002241897
111 0.002197563
112 0.002154105
113 0.002111507
114 0.002069751
115 0.002028821
116 0.0019887
117 0.001949373
118 0.001910823
119 0.001873036
120 0.001835996
121 0.001799688
122 0.001764099
123 0.001729213
124 0.001695017
125 0.001661497
126 0.001628641
127 0.001596434
128 0.001564864
129 0.001533918
130 0.001503584
131 0.00147385
132 0.001444704
133 0.001416134
134 0.00138813
135 0.001360679
136 0.001333771
137 0.001307395
138 0.001281541
139 0.001256198
140 0.001231356
141 0.001207006
142 0.001183137
143 0.00115974
144 0.001136805
145 0.001114325
146 0.001092288
147 0.001070688
148 0.001049515
149 0.00102876
150 0.001008416
151 0.000988474
152 0.000968927
153 0.000949766
154 0.000930984
155 0.000912573
156 0.000894527
157 0.000876837
158 0.000859497
159 0.0008425
160 0.00082584
161 0.000809508
162 0.0007935
163 0.000777808
164 0.000762427
165 0.000747349
166 0.00073257
167 0.000718083
168 0.000703883
169 0.000689964
170 0.000676319
171 0.000662945
172 0.000649835
173 0.000636984
174 0.000624387
175 0.00061204
176 0.000599937
177 0.000588073
178 0.000576443
179 0.000565044
180 0.00055387
181 0.000542917
182 0.000532181
183 0.000521656
184 0.00051134
185 0.000501229
186 0.000491317
187 0.000481601
188 0.000472077
189 0.000462741
190 0.00045359
191 0.00044462
192 0.000435828
193 0.000427209
194 0.000418761
195 0.00041048
196 0.000402362
197 0.000394406
198 0.000386606
199 0.000378961
200 0.000371467
and by simulation: 1 million successes (4-in-a-row 7s)
grouped data
items: 1,000,000
minimum value: 1.00
first quartile: 15.00
median: 35.00
third quartile: 70.00
maximum value: 717.00
wait freq
1 19601
2 19523
3 19097
4 18494
5 18109
6 17967
7 17488
8 17128
9 16983
10 16459
11 16149
12 15771
13 15484
14 15452
15 14860
16 14737
17 14319
18 14109
19 13714
20 13598
21 13152
22 12939
23 12575
24 12528
25 12107
26 12130
27 11662
28 11620
29 11443
30 11036
31 10978
32 10562
33 10587
34 10334
35 10002
36 9882
37 9493
38 9423
39 9458
40 8901
41 9058
42 8700
43 8537
44 8189
45 8227
46 8201
47 7897
48 7620
49 7542
50 7458
51 7280
52 7141
53 6968
54 6832
55 6652
56 6561
57 6580
58 6430
59 6227
60 6115
61 5867
62 5881
63 5719
64 5594
65 5516
66 5341
67 5308
68 5146
69 5027
70 5072
71 4845
72 4758
73 4794
74 4648
75 4486
76 4380
77 4400
78 4219
79 4193
80 4078
81 4006
82 3936
83 3775
84 3820
85 3707
86 3741
87 3549
88 3484
89 3445
90 3330
91 3194
92 3193
93 3107
94 3083
95 2978
96 2961
97 2976
98 2901
99 2795
100 2793
101 2708
102 2660
103 2628
104 2538
105 2563
106 2425
107 2441
108 2340
109 2258
110 2227
111 2270
112 2111
113 2147
114 2087
115 2029
116 2001
117 2008
118 1835
119 1878
120 1858
121 1825
122 1768
123 1730
124 1716
125 1737
126 1596
127 1614
128 1546
129 1561
130 1539
131 1453
132 1434
133 1419
134 1393
135 1241
136 1353
137 1258
138 1259
139 1317
140 1216
141 1212
142 1183
143 1146
144 1133
145 1119
146 1040
147 1123
148 970
149 1087
150 959
151 936
152 963
153 945
154 891
155 908
156 919
157 819
158 939
159 871
160 820
161 822
162 765
163 809
164 753
165 750
166 741
167 728
168 699
169 703
170 697
171 688
172 672
173 621
174 651
175 608
176 630
177 584
178 541
179 559
180 570
181 516
182 544
183 494
184 536
185 480
186 510
187 483
188 439
189 429
190 439
191 449
192 430
193 444
194 414
195 385
196 391
197 396
198 372
199 343
200 382
this might be what you want
and yes, you can code this in WinCraps too
i used a different program to simulate earlier
'for WinCraps Classic
When . . .
Initializing Auto-Bet
then . . .
Open/clear file for output: "attempts-4run7-before68.txt"
Name Chip-Stack # 0 as "# of 7s in a row (current)"
Name Chip-Stack # 1 as "# of 4run 7s in a row completed"
Name Chip-Stack # 2 as "attempts"
Bet $ 1 on Chip-Stack # 2
Go to "End"
While . . .
Number 6 or 8 has rolled each time
then . . .
Bet $ 0 on Chip-Stack # 0
Add $ 1 to Chip-Stack # 2
Go to "End"
' record current streak
While . . .
Any 7 has rolled each time
then . . .
Add $ 1 to Chip-Stack # 0
While . . .
Chip-Stack # 0 is equal to $ 4
then . . .
Output to file. Value of Chip-Stack # 2
Output to file. New line.
Bet $ 0 on Chip-Stack # 0
Add $ 1 to Chip-Stack # 1
Bet $ 1 on Chip-Stack # 2
End
When . . .
Chip-Stack # 1 is equal to $ 100000
then . . .
Stop Auto-Rolling / Hyper-Drive
Close file
the 1st 100 from a WC sim
attempt # freq
1 2033
2 2001
3 1864
4 1917
5 1880
6 1786
7 1681
8 1740
9 1660
10 1700
11 1599
12 1650
13 1573
14 1571
15 1448
16 1437
17 1461
18 1436
19 1338
20 1352
21 1263
22 1269
23 1337
24 1276
25 1227
26 1229
27 1156
28 1158
29 1144
30 1032
31 1100
32 1131
33 1003
34 1071
35 1021
36 949
37 958
38 929
39 860
40 895
41 876
42 873
43 884
44 864
45 828
46 784
47 793
48 784
49 784
50 798
51 721
52 716
53 746
54 696
55 672
56 645
57 661
58 638
59 604
60 629
61 563
62 565
63 542
64 563
65 505
66 555
67 553
68 476
69 541
70 518
71 494
72 427
73 473
74 466
75 454
76 439
77 448
78 404
79 379
80 391
81 401
82 367
83 410
84 362
85 358
86 387
87 354
88 375
89 348
90 309
91 341
92 319
93 330
94 292
95 304
96 326
97 253
98 266
99 278
100 294
winner and still champ...
#1
in other words
the FIRST attempt
I Heart Vi Hart


