Back to back "7's"
March 6th, 2014 at 4:34:35 PM
permalink
Can someone tell me the odds of back to back crap outs after points are established?
Need a little help with this one. Money on the line!!!!!
Need a little help with this one. Money on the line!!!!!
March 6th, 2014 at 4:42:01 PM
permalink
Quote: vegasrvpCan someone tell me the odds of back to back crap outs after points are established?
Need a little help with this one. Money on the line!!!!!
If you mean "point, 7, point, 7," one in 81. A point-7 is one in 9, happening back-to-back would happen once in 81 such scenarios.
March 6th, 2014 at 4:42:54 PM
permalink
Quote: vegasrvpCan someone tell me the odds of back to back crap outs after points are established?
Need a little help with this one. Money on the line!!!!!
If you mean like this point->seven->point->seven then the odds are
(2/3)*(1/6)*(2/3)*(1/6)=0.01234567901
March 6th, 2014 at 4:51:55 PM
permalink
Quote: geoffIf you mean like this point->seven->point->seven then the odds are
(2/3)*(1/6)*(2/3)*(1/6)=0.01234567901
Interesting number. Too bad .01234567890123456789... isn't something so "nice" looking as 1/81.
13717421 / 1111111111
March 6th, 2014 at 4:59:48 PM
permalink
Quote: wudgedQuote: geoffIf you mean like this point->seven->point->seven then the odds are
(2/3)*(1/6)*(2/3)*(1/6)=0.01234567901
Interesting number. Too bad .01234567890123456789... isn't something so "nice" looking as 1/81.
13717421 / 1111111111
Spoiler is a little off in terms of equaling 81. The actual number would be:
13,717,421 / 1,111,111,101
March 6th, 2014 at 5:14:51 PM
permalink
You mean to "7out"Quote: vegasrvpCan someone tell me the odds of back to back crap outs after points are established?
(a player can not "crap out" while a point is established, that only happens on come out rolls)
The probability of any 7out is
294/495
294/495 * 294/495 would be for the next 2 in a row (35.2764%)
so the odds against that event would be (1/(294/495)^2) - 1 to 1
or
1.834756352 to 1
Is this what you are looking for?
Sally
I Heart Vi Hart
March 6th, 2014 at 5:23:00 PM
permalink
Clearification:
I'm looking to compare 7 out 7 out versus hitting the point.
Sorry the misleading initial post.
I'm looking to compare 7 out 7 out versus hitting the point.
Sorry the misleading initial post.
March 6th, 2014 at 5:24:48 PM
permalink
Clearification:
I am not using the proper language I guess.
I'm looking to see the odds on throwing a 7 after point is established two times in a row without hitting the point?
Hope this is more clear.
I am not using the proper language I guess.
I'm looking to see the odds on throwing a 7 after point is established two times in a row without hitting the point?
Hope this is more clear.
March 6th, 2014 at 5:32:51 PM
permalink
Quote: vegasrvpClearification:
I am not using the proper language I guess.
I'm looking to see the odds on throwing a 7 after point is established two times in a row without hitting the point?
Hope this is more clear.
So you want to calculate, given that a point is already established, what are the chances are of sevening out, and then throwing a winner 7 immediately on the come out?
example -- given a point of 4, you want to know the chances of at some point sevening out and then immediately throwing a seven on the come out?
It depends on the point:
for 4 and 10 your chances are 2/3 * 1/6 = 1/9
for 5 and 9 your chances are 3/5 * 1/6 = 1/10
for 6 and 8 your chances are 6/11 * 1/6 = 1/11
If you don't know the point, you have to do weighted probabilities:
5/12 of the time, your point will be a 6 or an 8. So 5/12 * 1/11 = 5/132
4/12 of the time, your point will be a 5 or a 9. So 4/12 * 1/10 = 1/30
3/12 of the time, your point will be a 4 or a 10. So 3/12 * 1/9 = 1/36
Add them all together, 1/36 + 1/30 + 5/132 and you get a grand total of 49/495 -- which I believe is the answer you're looking for.
March 6th, 2014 at 5:38:37 PM
permalink
Here is a specific example:
Roll 6
6 is the point
no matter how many rolls I am looking for 7 before the point.
Once 7 is rolled a new point is established;
Roll 8
Again no matter how many rolls a 7 is rolled before the point.
That is two 7 outs before a point is won.
The question is what are the odds that no winner will be rolled prior to two 7 outs.
If we call a winner point or loser 7out no point a session then I am looking to find out how many times is average between back to back loser 7 rolls?
Clearer yet. I HOPE.
Roll 6
6 is the point
no matter how many rolls I am looking for 7 before the point.
Once 7 is rolled a new point is established;
Roll 8
Again no matter how many rolls a 7 is rolled before the point.
That is two 7 outs before a point is won.
The question is what are the odds that no winner will be rolled prior to two 7 outs.
If we call a winner point or loser 7out no point a session then I am looking to find out how many times is average between back to back loser 7 rolls?
Clearer yet. I HOPE.
March 6th, 2014 at 5:46:25 PM
permalink
Quote: vegasrvpHere is a specific example:
Roll 6
6 is the point
no matter how many rolls I am looking for 7 before the point.
Once 7 is rolled a new point is established;
Roll 8
Again no matter how many rolls a 7 is rolled before the point.
That is two 7 outs before a point is won.
The question is what are the odds that no winner will be rolled prior to two 7 outs.
If we call a winner point or loser 7out no point a session then I am looking to find out how many times is average between back to back loser 7 rolls?
Clearer yet. I HOPE.
I believe the question you are asking is what are the chances the next two shooters each 7-out before making a point.
5/12 of the time, your point will be a 6 or an 8. Your chances of losing the 6 or 8 are 6/11. 5/12*6/11 = 5/22
4/12 of the time, your point will be a 5 or a 9. Your chances of losing the 5 or 9 are 3/5. 4/12*3/5 = 1/5
3/12 of the time, your point will be a 4 or a 10. Your chances of losing the 4 or 10 are 2/3. 3/12*2/3= 1/6
5/22 + 1/6 +1/5 = 98/165 = the chance of sevening out once you establish an unknown point.
losing an unknown point two shooters in a row (not counting rolls where you win or lose on the come out)= (98/165)^2 = 9604/27225 = 35.28%
Edited my post due to error pointed out by MustangSally
March 6th, 2014 at 5:52:58 PM
permalink
Ok so odds of...a point rolled on first CO roll + a 7 is rolled before that point is hit + another point is established on first CO roll + a 7 is again rolled before that point is hit
March 6th, 2014 at 5:57:00 PM
permalink
Quote: hwccdealerQuote: wudgedQuote: geoffIf you mean like this point->seven->point->seven then the odds are
(2/3)*(1/6)*(2/3)*(1/6)=0.01234567901
Interesting number. Too bad .01234567890123456789... isn't something so "nice" looking as 1/81.
13717421 / 1111111111
Spoiler is a little off in terms of equaling 81. The actual number would be:
13,717,421 / 1,111,111,101
Yea, I was giving the fraction for 0.0123456789... which is different from 1/81 (which is all digits in order except for the 8)
March 6th, 2014 at 6:01:11 PM
permalink
A friend of mine has come to me with an idea about a system base solely on the don't pass wager with no odds. I tried to stop him right there but he insisted this was viable.
Now I am looking for math to back up my argument.
He wants to use a version of martingale system.
The betting system he has is 1, 1, 1, 2, 2, 4, 4, 8, 8, ect......
The loss moves you up the system and a win triggers a double up on he next roll.
He thinks the 2 / 3 win and 12 push or 7 / 11 loss on the come out roll just move you through the system the same way.
Here is a sample roll
Bet 1 unit come out roll = 6 point
rolling 4, 8, 8 ,9 6 winner lose 1 unit
Bet 1 unit come out roll = 4 point
rolling 5, 6, 5, 8, 7 out winner 1 unit (so next wager is 2 units)
Bet 2 units come out roll = 9 point
rolling 4,12,4,8,6,5,6,6,8,7 out winner 4 units back to beginning
If 2 or 3 hit on the come out roll it is a win, and you either move to double or back to beginning if it finishes a session.
12 on come out is a push not blood
7 or 11 on the come out roll is a loss and move to next level of the system.
His argument is he can win by hitting 2 "7's" or even a 7 out followed by a 3 before hitting 10-15 points winners.
I know this is pretty off the wall, and I know in my gut it is a failure, but I was hoping to have some math to back my argument and I am not even sure this will deter him.
Now I am looking for math to back up my argument.
He wants to use a version of martingale system.
The betting system he has is 1, 1, 1, 2, 2, 4, 4, 8, 8, ect......
The loss moves you up the system and a win triggers a double up on he next roll.
He thinks the 2 / 3 win and 12 push or 7 / 11 loss on the come out roll just move you through the system the same way.
Here is a sample roll
Bet 1 unit come out roll = 6 point
rolling 4, 8, 8 ,9 6 winner lose 1 unit
Bet 1 unit come out roll = 4 point
rolling 5, 6, 5, 8, 7 out winner 1 unit (so next wager is 2 units)
Bet 2 units come out roll = 9 point
rolling 4,12,4,8,6,5,6,6,8,7 out winner 4 units back to beginning
If 2 or 3 hit on the come out roll it is a win, and you either move to double or back to beginning if it finishes a session.
12 on come out is a push not blood
7 or 11 on the come out roll is a loss and move to next level of the system.
His argument is he can win by hitting 2 "7's" or even a 7 out followed by a 3 before hitting 10-15 points winners.
I know this is pretty off the wall, and I know in my gut it is a failure, but I was hoping to have some math to back my argument and I am not even sure this will deter him.
March 6th, 2014 at 6:03:19 PM
permalink
how can that be correct?Quote: sodawaterlosing an unknown point two shooters in a row (not counting rolls where you win or lose on the come out)= (49/78) ^2 =2401/6084 = 39.46%
the Wizard says the probability of winning any point = 201/495 = 0.406061
https://wizardofodds.com/ask-the-wizard/craps/probability/
that makes 294/495 the probability of not winning any point
so my earlier post is correct for the next 2 shooters NOT hitting a point
Both 7out
if that is what the OP wants
But the OP wants to know something else about how long will it take?
"out how many times is average between back to back loser 7 rolls"
is this the same as back to back point losers?
I think it might be
but he started another thread where it looks like he wants to know how many pass line winners before 2 point losers in a row
https://wizardofvegas.com/forum/gambling/craps/17326-prove-me-wrong/
I guess this leads down a long and winding road?
I see a new post about a betting system!
yea!
Sally
I Heart Vi Hart
March 6th, 2014 at 6:03:22 PM
permalink
A friend of mine has come to me with an idea about a system base solely on the don't pass wager with no odds. I tried to stop him right there but he insisted this was viable.
Now I am looking for math to back up my argument.
He wants to use a version of martingale system.
The betting system he has is 1, 1, 1, 2, 2, 4, 4, 8, 8, ect......
The loss moves you up the system and a win triggers a double up on he next roll.
He thinks the 2 / 3 win and 12 push or 7 / 11 loss on the come out roll just move you through the system the same way.
Here is a sample roll
Bet 1 unit come out roll = 6 point
rolling 4, 8, 8 ,9 6 winner lose 1 unit
Bet 1 unit come out roll = 4 point
rolling 5, 6, 5, 8, 7 out winner 1 unit (so next wager is 2 units)
Bet 2 units come out roll = 9 point
rolling 4,12,4,8,6,5,6,6,8,7 out winner 4 units back to beginning
If 2 or 3 hit on the come out roll it is a win, and you either move to double or back to beginning if it finishes a session.
12 on come out is a push not blood
7 or 11 on the come out roll is a loss and move to next level of the system.
His argument is he can win by hitting 2 "7's" or even a 7 out followed by a 3 before hitting 10-15 points winners.
I know this is pretty off the wall, and I know in my gut it is a failure, but I was hoping to have some math to back my argument and I am not even sure this will deter him.
Now I am looking for math to back up my argument.
He wants to use a version of martingale system.
The betting system he has is 1, 1, 1, 2, 2, 4, 4, 8, 8, ect......
The loss moves you up the system and a win triggers a double up on he next roll.
He thinks the 2 / 3 win and 12 push or 7 / 11 loss on the come out roll just move you through the system the same way.
Here is a sample roll
Bet 1 unit come out roll = 6 point
rolling 4, 8, 8 ,9 6 winner lose 1 unit
Bet 1 unit come out roll = 4 point
rolling 5, 6, 5, 8, 7 out winner 1 unit (so next wager is 2 units)
Bet 2 units come out roll = 9 point
rolling 4,12,4,8,6,5,6,6,8,7 out winner 4 units back to beginning
If 2 or 3 hit on the come out roll it is a win, and you either move to double or back to beginning if it finishes a session.
12 on come out is a push not blood
7 or 11 on the come out roll is a loss and move to next level of the system.
His argument is he can win by hitting 2 "7's" or even a 7 out followed by a 3 before hitting 10-15 points winners.
I know this is pretty off the wall, and I know in my gut it is a failure, but I was hoping to have some math to back my argument and I am not even sure this will deter him.
March 6th, 2014 at 6:14:10 PM
permalink
Quote: mustangsallyhow can that be correct?
You are right, I messed up adding the fractions at the very end. I've edited my post and my math now agrees with your post.
March 6th, 2014 at 9:44:44 PM
permalink
There is no being system that will defeat the house edge other than the Martingale with an unlimited bankroll and a no limit table.
March 6th, 2014 at 10:16:02 PM
permalink
Quote: TerribleTomThere is no being system that will defeat the house edge other than the Martingale with an unlimited bankroll and a no limit table.
even that wont work long term
March 6th, 2014 at 10:48:29 PM
permalink
Quote: vegasrvpA friend of mine has come to me with an idea about a system base solely on the don't pass wager with no odds. I tried to stop him right there but he insisted this was viable.
Now I am looking for math to back up my argument.
He wants to use a version of martingale system.
The betting system he has is 1, 1, 1, 2, 2, 4, 4, 8, 8, ect......
The loss moves you up the system and a win triggers a double up on he next roll.
I thought of the same thing, except the progression was: 1 22 333 4444 -- you get the idea. I wrote a program to simm this, and it looked like it was the real deal.
That was until I took a good look at the results and saw how odd the data looked. Turned out that Python's randint function doesn't work right until the system's been on long enough to develop enough entropy. Simms done later in the day showed the expected results: lots of small wins and a few horrendous losses. Actual results with good data were right about a fraction of a percentage point within known expectation for the Don't Pass.
Any Martingale, even a "soft" one, is headed for disaster. This is especially true for Craps, as long hands, or even a series of shooters with a few passes between them, are not all that uncommon. Best way to play is bet the Don't, lay odds, take what you can and get out if you lose two in a row.
Depending on how frequently he plays, he might get away with it for a good long while, but the Day of Reckoning will come.
March 7th, 2014 at 12:34:44 PM
permalink
My thoughts exactly.......now that being said let's look at this potential option......I cannot believe i just said that. LOL
Based on his method of 1,1,1,2,2,4,4,8,8,16,16,32,32 & 64. This would fit within all table limits even with the double down.
It would also leave a total loss maximum of 191 units (@ $10 that is $1910).
The question is can you win small ones enough times to cover the few large losses.
With the dice game no history matters so trends are pure luck either good or bad depending on your side of the wager.
All math states odds are in our favor for no point vs point being achieved.
Do you believe that more times then not you could win 191 units between the big losses?
You can do things like never wager on a shooter that hits more then one number. You can change tables after every win or loss to eliminate a hit shooter (as if there is a real thing).
The two things I like about what he has proposed is there is a win on every session and also if you hit the two in a row in the right place it could be a multi-unit win which means your progress is increased exponentially.
If I were to try to argue the other side I am starting to see some small validity based on the knowledge that many small wins can and most likely will eventually get wasted by the big loss.
I messed around a little last night online and made 50 units in 16 sessions which in table time may have been about 2-3 hours. I had one session go to the second 8 unit wager and 2 times to the first 8. Otherwise 12 of the 16 wins came in the first 5 wager options.
If I were to build in stop losses and go at this I would probable do so with a stop loss after the first 32. That is a total loss of 95 units. Based on what I just did last night I won 50 of the 95 units needed to build a second bank.
Lastly, can you tell me why you would use a progression like the one you mentioned (1,2,2,3,3,3,4,4,4,4,5,5,5,5,5)? This to me makes no sense based on what I am looking at as once you pass the 3's you are now playing to achieve a loss? Unless I am not understanding your playing?
Based on his method of 1,1,1,2,2,4,4,8,8,16,16,32,32 & 64. This would fit within all table limits even with the double down.
It would also leave a total loss maximum of 191 units (@ $10 that is $1910).
The question is can you win small ones enough times to cover the few large losses.
With the dice game no history matters so trends are pure luck either good or bad depending on your side of the wager.
All math states odds are in our favor for no point vs point being achieved.
Do you believe that more times then not you could win 191 units between the big losses?
You can do things like never wager on a shooter that hits more then one number. You can change tables after every win or loss to eliminate a hit shooter (as if there is a real thing).
The two things I like about what he has proposed is there is a win on every session and also if you hit the two in a row in the right place it could be a multi-unit win which means your progress is increased exponentially.
If I were to try to argue the other side I am starting to see some small validity based on the knowledge that many small wins can and most likely will eventually get wasted by the big loss.
I messed around a little last night online and made 50 units in 16 sessions which in table time may have been about 2-3 hours. I had one session go to the second 8 unit wager and 2 times to the first 8. Otherwise 12 of the 16 wins came in the first 5 wager options.
If I were to build in stop losses and go at this I would probable do so with a stop loss after the first 32. That is a total loss of 95 units. Based on what I just did last night I won 50 of the 95 units needed to build a second bank.
Lastly, can you tell me why you would use a progression like the one you mentioned (1,2,2,3,3,3,4,4,4,4,5,5,5,5,5)? This to me makes no sense based on what I am looking at as once you pass the 3's you are now playing to achieve a loss? Unless I am not understanding your playing?
March 7th, 2014 at 12:41:23 PM
permalink
With an unlimited bankroll and a no limit table then martingale works. The issue is that in real life there are no tables without limits and an unlimited bankroll doesn't exist.Quote: sodawatereven that wont work long term
March 7th, 2014 at 12:58:32 PM
permalink
Quote: geoffWith an unlimited bankroll and a no limit table then martingale works. The issue is that in real life there are no tables without limits and an unlimited bankroll doesn't exist.
in a negative game, it still doesn't work long term.
March 7th, 2014 at 1:11:43 PM
permalink
this information is useless to you because you said you (your friend) bet on the don't pass and that can lose when a point is not established and most time it does lose is on the come out roll.Quote: vegasrvpWith the dice game no history matters so trends are pure luck either good or bad depending on your side of the wager.
All math states odds are in our favor for no point vs point being achieved.
me too but not online ;)Quote: vegasrvpI messed around a little last night online
I programmed a file to be run in WinCraps Classic and ran it 5000 times
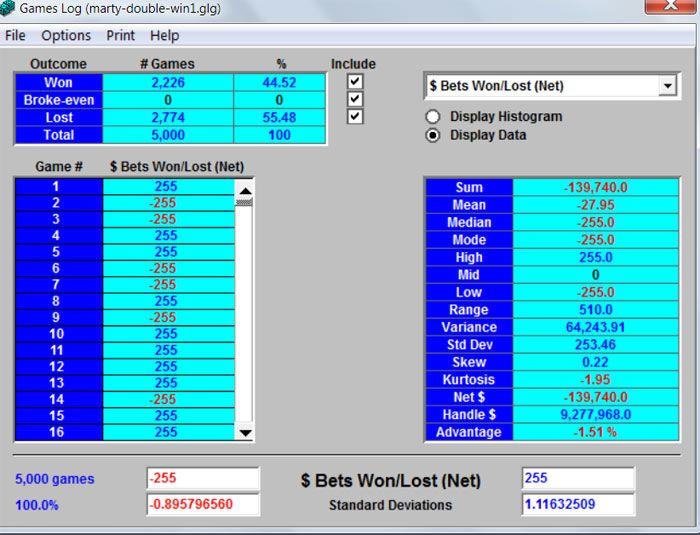
a snap of the game log window
the file I used
When . . .
Initializing Auto-Bet
then . . .
Bet $ 1 on Chip-Stack # 0
Bet $ 1 on Chip-Stack # 1
Bet $ 1 on Chip-Stack # 2
Bet $ 1 on Chip-Stack # 3
Bet $ 2 on Chip-Stack # 4
Bet $ 2 on Chip-Stack # 5
Bet $ 4 on Chip-Stack # 6
Bet $ 4 on Chip-Stack # 7
Bet $ 8 on Chip-Stack # 8
Bet $ 8 on Chip-Stack # 9
Bet $ 16 on Chip-Stack # 10
Bet $ 16 on Chip-Stack # 11
Bet $ 32 on Chip-Stack # 12
Bet $ 32 on Chip-Stack # 13
Bet $ 64 on Chip-Stack # 14
Bet $ 64 on Chip-Stack # 15
Bet 100 % of Chip-Stack ref # 0 on Don't Pass
Go to "end"
While . . .
Don't Pass has lost each time
then . . .
Go to "loss"
While . . .
Don't Pass has won each time
then . . .
Go to "win"
else . . .
Go to "end"
loss
While . . .
Don't Pass has lost each time
Chip-Stack # 0 is less than $ 15
then . . .
Add $ 1 to Chip-Stack # 0
Bet 100 % of Chip-Stack ref # 0 on Don't Pass
Go to "status"
While . . .
Don't Pass has lost each time
Chip-Stack # 0 is not less than $ 15
then . . .
Add $ 1 to Chip-Stack # 0
Bet 100 % of Chip-Stack # 15 on Don't Pass
Go to "status"
win
While . . .
Don't Pass has won 1 time
then . . .
Bet 200 % of the last Don't Pass on Don't Pass
Go to "status"
While . . .
Don't Pass has won 2 times
then . . .
Bet $ 1 on Chip-Stack # 0
Bet 100 % of Chip-Stack ref # 0 on Don't Pass
Reset wins / losses on Don't Pass
status
While . . .
Bankroll is equal to $ 0
or while . . .
Bankroll is not less than $ 510
then . . .
Add $ 1 to Chip-Stack # 19
Bet $ 1 on Chip-Stack # 0
Bet 100 % of highest bankroll on Chip-Stack # 17
Reset table (preserve Chip-Stacks)
Bet $ 0 on Chip-Stack # 17
Bet 100 % of Chip-Stack ref # 0 on Don't Pass
When . . .
Chip-Stack # 19 is equal to $ 5000
then . . .
Stop Auto-Rolling / Hyper-Drive
end
'adjust dpass to hit target
While . . .
Don't Pass has lost each time
or while . . .
Don't Pass has won each time
then . . .
Bet 100 % of bankroll on Chip-Stack # 18
Add 100 % of Don't Pass to Chip-Stack # 18
Subtract $ 510 from Chip-Stack # 18
While . . .
Chip-Stack # 18 is greater than $ 0
then . . .
Subtract 100 % of Chip-Stack # 18 from Don't Pass
Bet $ 0 on Chip-Stack # 18
Initializing Auto-Bet
then . . .
Bet $ 1 on Chip-Stack # 0
Bet $ 1 on Chip-Stack # 1
Bet $ 1 on Chip-Stack # 2
Bet $ 1 on Chip-Stack # 3
Bet $ 2 on Chip-Stack # 4
Bet $ 2 on Chip-Stack # 5
Bet $ 4 on Chip-Stack # 6
Bet $ 4 on Chip-Stack # 7
Bet $ 8 on Chip-Stack # 8
Bet $ 8 on Chip-Stack # 9
Bet $ 16 on Chip-Stack # 10
Bet $ 16 on Chip-Stack # 11
Bet $ 32 on Chip-Stack # 12
Bet $ 32 on Chip-Stack # 13
Bet $ 64 on Chip-Stack # 14
Bet $ 64 on Chip-Stack # 15
Bet 100 % of Chip-Stack ref # 0 on Don't Pass
Go to "end"
While . . .
Don't Pass has lost each time
then . . .
Go to "loss"
While . . .
Don't Pass has won each time
then . . .
Go to "win"
else . . .
Go to "end"
loss
While . . .
Don't Pass has lost each time
Chip-Stack # 0 is less than $ 15
then . . .
Add $ 1 to Chip-Stack # 0
Bet 100 % of Chip-Stack ref # 0 on Don't Pass
Go to "status"
While . . .
Don't Pass has lost each time
Chip-Stack # 0 is not less than $ 15
then . . .
Add $ 1 to Chip-Stack # 0
Bet 100 % of Chip-Stack # 15 on Don't Pass
Go to "status"
win
While . . .
Don't Pass has won 1 time
then . . .
Bet 200 % of the last Don't Pass on Don't Pass
Go to "status"
While . . .
Don't Pass has won 2 times
then . . .
Bet $ 1 on Chip-Stack # 0
Bet 100 % of Chip-Stack ref # 0 on Don't Pass
Reset wins / losses on Don't Pass
status
While . . .
Bankroll is equal to $ 0
or while . . .
Bankroll is not less than $ 510
then . . .
Add $ 1 to Chip-Stack # 19
Bet $ 1 on Chip-Stack # 0
Bet 100 % of highest bankroll on Chip-Stack # 17
Reset table (preserve Chip-Stacks)
Bet $ 0 on Chip-Stack # 17
Bet 100 % of Chip-Stack ref # 0 on Don't Pass
When . . .
Chip-Stack # 19 is equal to $ 5000
then . . .
Stop Auto-Rolling / Hyper-Drive
end
'adjust dpass to hit target
While . . .
Don't Pass has lost each time
or while . . .
Don't Pass has won each time
then . . .
Bet 100 % of bankroll on Chip-Stack # 18
Add 100 % of Don't Pass to Chip-Stack # 18
Subtract $ 510 from Chip-Stack # 18
While . . .
Chip-Stack # 18 is greater than $ 0
then . . .
Subtract 100 % of Chip-Stack # 18 from Don't Pass
Bet $ 0 on Chip-Stack # 18
I used the 64 unit bet as tops for a 255 unit bankroll
I wanted to see what this could do with a nice bankroll
It can double that about 44% of the time (44 out of 100 or 56 times losing all 255 units)
the other times it lost all 255 units
so the math bears out (from simulations) another losing system but may be fun to play and should gain some nice comps.
This one looks to lose on average $28 per session played, again an average over time for each session played
there are systems that do way worse and some better
I would think a progression on the odds bet for the don't pass would be more fun, thrilling and more profitable than
what you have explained.
Sally
I Heart Vi Hart
March 7th, 2014 at 1:20:52 PM
permalink
Sally,
Thanks, that is so nice of you to do this.
I'm a little unsure about what you said regarding
"this information is useless to you because you said you (your friend) bet on the don't pass and that can lose when a point is not established and most time it does lose is on the come out roll."
Is this simulation based on playing the Pass or the Don't?
Thanks, that is so nice of you to do this.
I'm a little unsure about what you said regarding
"this information is useless to you because you said you (your friend) bet on the don't pass and that can lose when a point is not established and most time it does lose is on the come out roll."
Is this simulation based on playing the Pass or the Don't?
March 7th, 2014 at 1:25:34 PM
permalink
Quote: vegasrvpCan someone tell me the odds of back to back crap outs after points are established?
Need a little help with this one. Money on the line!!!!!
Simple answer to a simple question.
back to back = 3:14
back to back to back = 3:28
(Don't ask how I know, I just know).
Sorry I just read title "back to back 7's" I thought the question was back to back craps numbers.
carry on... :0
8 more years till retirement.
March 7th, 2014 at 1:36:02 PM
permalink
Quote: vegasrvpClearification:
I'm looking to compare 7 out 7 out versus hitting the point.
Sorry the misleading initial post.
Easy answer.
look around the table for random shooters and your answer will be:
per table round of random shooters
11:14 will 7-out before a point is made.
2:14 will make a point or two before 7 out
1:14 will make enough points to win back a majority of losses incurred from the previous shooters.
(Sometimes photographic memory with 15+ years of live table craps experience is better than math)
Another good question would be:
How many numbers rolled between the "point" and "7-out"
if DI is the shooter then the answer is 4 both ways.
Again don't ask how I get these figures, but they are extremely accurate. :)
8 more years till retirement.
March 7th, 2014 at 3:07:19 PM
permalink
You are welcome. I said I was also fooling around too.Quote: vegasrvpSally,
Thanks, that is so nice of you to do this.
I'm a little unsure about what you said regarding
"this information is useless to you because you said you (your friend) bet on the don't pass and that can lose when a point is not established and most time it does lose is on the come out roll."
Is this simulation based on playing the Pass or the Don't?
The sim was for the don't pass and can seen in the code I also posted
(I am sure the same results would also be with the pass line bet too)
now, I meant to say something different instead of
"... does lose is on the come out roll."
I say now
"... does lose is after the come out roll on average.
8/36 / 976/1980 = 55/122 or about 45.08197% of the times the don't pass has lost has lost on the come out roll
67/122 during the point round (54.91803%)"
But a system that can double a bankroll in 45% of its sessions can be fun for some, not for all who try
still has the short end of the stick
Sally
I Heart Vi Hart
March 7th, 2014 at 4:28:37 PM
permalink
I disagree. The first point-7 doesn't count because you can't have a second point-7 until the first is established. 1 in 9 is the correct answer.Quote: hwccdealerIf you mean "point, 7, point, 7," one in 81. A point-7 is one in 9, happening back-to-back would happen once in 81 such scenarios.
Someday, joor goin' to see the name of Googie Gomez in lights and joor goin' to say to joorself, "Was that her?" and then joor goin' to answer to joorself, "That was her!" But you know somethin' mister? I was always her yuss nobody knows it! - Googie Gomez
March 7th, 2014 at 4:47:55 PM
permalink
Quote: sodawaterin a negative game, it still doesn't work long term.
Please explain.
Martingale is simple. Double your bet if you lose.
Craps, roulette, flipping coins - the game does not matter.
Bet 1, lose
Bet 2, lose
Bet 4, lose
Bet 8, win = net gain of 1, start over.
Whether you're betting black/red, pass/don't pass, head or tails, it matters not. If your bankroll is unlimited and there is no limit to the betting, eventually you're going to win and when you do you're going to be up by the original bet.
I guess one could theoretically flip a coin and get tails every time from here until eternity, but in reality you are eventually going to win and when you do you're going to be up $1.
Even with roulette, the green won't matter. Bet on black every time and eventually it's going to come up black. When it does, start over at 1.
Of course nobody has an infinite bankroll and even no limit tables will eventually have limits when the casino realizes you're ready to wager $5M to win $1...
If I'm missing something, please enlighten me.
March 7th, 2014 at 5:19:14 PM
permalink
Isn't that chance 1/infinity and that limit is 0?Quote: TerribleTomI guess one could theoretically flip a coin and get tails every time from here until eternity, but in reality you are eventually going to win and when you do you're going to be up $1.
Interesting concept
eventually you will win with unlimited casino credit and no max table limits
why?
because the chance of winning (or probability) is 1/the largest number you can make
still higher than 0
is it?
http://www.mathsisfun.com/calculus/limits-infinity.html
or is that still 1/infinity = 0 or is it?
so the probability of losing every bet over infinity = 0
the probability of winning just 1 time in infinity is also 0 (1/infinity)
coins are so dirty
TITO
Sally
I Heart Vi Hart
March 7th, 2014 at 7:09:34 PM
permalink
Maybe it's -1/12Quote: mustangsallyor is that still 1/infinity = 0 or is it?
Someday, joor goin' to see the name of Googie Gomez in lights and joor goin' to say to joorself, "Was that her?" and then joor goin' to answer to joorself, "That was her!" But you know somethin' mister? I was always her yuss nobody knows it! - Googie Gomez
March 7th, 2014 at 7:42:27 PM
permalink
Sally,
I was reviewing this info again and came up with another questions.
You stated in this run:
"It can double that about 44% of the time (44 out of 100 or 56 times losing all 255 units)
the other times it lost all 255 units"
Are you stating the in 100 rounds you would double up 44% of the time and 56% of the time lose all 255 units?
That means based on what I was questioning that 56% of the time we will hit 14 points without rolling a 7 out? Or are you stating in 5000 rounds there were 255 times you lost it all?
I was reviewing this info again and came up with another questions.
You stated in this run:
"It can double that about 44% of the time (44 out of 100 or 56 times losing all 255 units)
the other times it lost all 255 units"
Are you stating the in 100 rounds you would double up 44% of the time and 56% of the time lose all 255 units?
That means based on what I was questioning that 56% of the time we will hit 14 points without rolling a 7 out? Or are you stating in 5000 rounds there were 255 times you lost it all?
March 7th, 2014 at 7:54:35 PM
permalink
Quote: mustangsallyIsn't that chance 1/infinity and that limit is 0?
Interesting concept
eventually you will win with unlimited casino credit and no max table limits
why?
because the chance of winning (or probability) is 1/the largest number you can make
still higher than 0
is it?
http://www.mathsisfun.com/calculus/limits-infinity.html
or is that still 1/infinity = 0 or is it?
so the probability of losing every bet over infinity = 0
the probability of winning just 1 time in infinity is also 0 (1/infinity)
coins are so dirty
TITO
Sally
I don't understand. 1/infinity is never zero. It's undefined so it's never anything.
March 7th, 2014 at 9:55:58 PM
permalink
yes, per 100 sessions of playQuote: vegasrvp"It can double that about 44% of the time (44 out of 100 or 56 times losing all 255 units)
the other times it lost all 255 units"
Are you stating the in 100 rounds you would double up 44% of the time and 56% of the time lose all 255 units?
double up or bust out trying
Quote: vegasrvpThat means based on what I was questioning that 56% of the time we will hit 14 points without rolling a 7 out?
where do you get 14 points from?
the don't pass loses 45% of the time on average, sometimes higher sometimes lower,
on the come out roll on a 7 or an 11
the photo shows that in 5000 roundsQuote: vegasrvpOr are you stating in 5000 rounds there were 255 times you lost it all?
2226 sessions ended by turning a 255 unit bankroll into 510 units
2774 sessions lost all 255 units - busted.
I did not track how many losses came on the come out roll and during the point round
I am sure that ratio on average is about 45/55%
when one bets the don't pass on the come out roll, a 7 or an 11 rolled right there causes the don't pass to lose and your progression to move up one step.
That can happen 3-4 times in a row before a point is ever established.
And if you do not win your parlay bet, another loss and a move up to the next step
so if you go a bunch of bets without ever winning 2 in a row, you end up losing
unless I did not understand what you wrote about playing this method.
Sally
I Heart Vi Hart
March 8th, 2014 at 1:02:49 AM
permalink
Quote: geoffI don't understand. 1/infinity is never zero. It's undefined so it's never anything.
Exactly. The results of Martingale with an infinite bankroll are also undefined and therefore also never anything.
Here is a good rule of thumb: if you add up a bunch of numbers that are all negative, and you get a positive number (or vice versa) your math is wrong.
March 8th, 2014 at 11:38:01 AM
permalink
To me the most important part is what you are considering a loss vs what I am considering a loss.
In order to bust out and lose 255 units you will have to lose on either a 7 / 11 on the come out roll of the player will have to make their point.
in order to get 255 units lost you will have to lose the wager based on the following sequence:
1, 1, 1, 2, 2, 4, 4, 8, 8, 16, 16, 32, 32, 64, 64.
That is 15 losses with hitting back to back 7 once point is established.
Roll example:
point come out roll is 6
Rolls of 2,5,9,8,8,5,4,11,12,6 winner means lose bet 1 move to next level
point come out roll is 7
Lose bet 1
move to next level
point come out roll is 11
lose bet 1
move to next level
point come out roll is 5
rolls of 4,8,9,3,8,6,6,5 pint winner
lose bet 2
move to next level
point come out roll is 3
winner win bet 2
move to next level double 2 (4)
point come out roll is 9
rolls of 4,6,5,10,3,5,2,7 out
winner of 8 units (less bets of 1,1,1,2 = 8-7=+1 unit for session)
Session complete move back to beginning
Based on the sequence of 1, 1, 1, 2, 2, 4, 4, 8, 8, 16, 16, 32, 32, 64, 64.
If you win you double down and if you win again you start over.
If you lose you move forward in the sequence
on the come out roll you will win with 2 / 3 lose on 7 / 11 and push on 12.
Based on win or loss move forward of double accordingly.
Based on this methodology you will have to either hit 7 / 11 on the come out roll or win 15 point (or some combination).
BEFORE
You hit 2/3 on the come out roll back to back, 7 out on the point (or some combination).
Is this what you thought? Also is this more clear?
In order to bust out and lose 255 units you will have to lose on either a 7 / 11 on the come out roll of the player will have to make their point.
in order to get 255 units lost you will have to lose the wager based on the following sequence:
1, 1, 1, 2, 2, 4, 4, 8, 8, 16, 16, 32, 32, 64, 64.
That is 15 losses with hitting back to back 7 once point is established.
Roll example:
point come out roll is 6
Rolls of 2,5,9,8,8,5,4,11,12,6 winner means lose bet 1 move to next level
point come out roll is 7
Lose bet 1
move to next level
point come out roll is 11
lose bet 1
move to next level
point come out roll is 5
rolls of 4,8,9,3,8,6,6,5 pint winner
lose bet 2
move to next level
point come out roll is 3
winner win bet 2
move to next level double 2 (4)
point come out roll is 9
rolls of 4,6,5,10,3,5,2,7 out
winner of 8 units (less bets of 1,1,1,2 = 8-7=+1 unit for session)
Session complete move back to beginning
Based on the sequence of 1, 1, 1, 2, 2, 4, 4, 8, 8, 16, 16, 32, 32, 64, 64.
If you win you double down and if you win again you start over.
If you lose you move forward in the sequence
on the come out roll you will win with 2 / 3 lose on 7 / 11 and push on 12.
Based on win or loss move forward of double accordingly.
Based on this methodology you will have to either hit 7 / 11 on the come out roll or win 15 point (or some combination).
BEFORE
You hit 2/3 on the come out roll back to back, 7 out on the point (or some combination).
Is this what you thought? Also is this more clear?
March 8th, 2014 at 11:55:34 AM
permalink
Here is some info I gathered on this site from other locations. Does this fit into what you are seeing?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
What is the average number of points hit by a craps shooter before he sevens out?
— JimmyMac
Given that a point is established, the probability that the shooter makes the point is pr(point is 4 or 10) ×pr(making 4 or 10) + pr(point is 5 or 9) × pr(making 5 or 9) + pr(point is 6 or 8) ×pr(making 6 or 8) = (6/24) × (3/9) + (8/24) × (4/10) + (10/24) × (5/11) = 201/495 = 0.406061.
If the probability of an event is p, then the expected number of times it will happen before failure is p/(1-p). So, the expected number of points per shooter is 0.406061/(1-0.406061) = 0.683673.
This question was raised and discussed in the forum of my companion site Wizard of Vegas .
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I had run a sim (not me this is on the site) of 8,522,945 million dice rolls. Here are those results:
1,000,000/shooters
682796/total points wins
count points wins % or more or less
594110 0 0.5941100000
241267 1 0.2412670000 0.4058900000 0.8353770000
97983 2 0.0979830000 0.1646230000 0.9333600000
39547 3 0.0395470000 0.0666400000 0.9729070000
16136 4 0.0161360000 0.0270930000 0.9890430000
6535 5 0.0065350000 0.0109570000 0.9955780000
2596 6 0.0025960000 0.0044220000 0.9981740000
1067 7 0.0010670000 0.0018260000 0.9992410000
425 8 0.0004250000 0.0007590000 0.9996660000
188 9 0.0001880000 0.0003340000 0.9998540000
91 10 0.0000910000 0.0001460000 0.9999450000
55 11+ 0.0000550000 0.0000550000 1.0000000000
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
If I am reading this right based on 1 million shooters 55 times a shooter hit 11 or more points?
This seems like a much more realistic number.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
What is the average number of points hit by a craps shooter before he sevens out?
— JimmyMac
Given that a point is established, the probability that the shooter makes the point is pr(point is 4 or 10) ×pr(making 4 or 10) + pr(point is 5 or 9) × pr(making 5 or 9) + pr(point is 6 or 8) ×pr(making 6 or 8) = (6/24) × (3/9) + (8/24) × (4/10) + (10/24) × (5/11) = 201/495 = 0.406061.
If the probability of an event is p, then the expected number of times it will happen before failure is p/(1-p). So, the expected number of points per shooter is 0.406061/(1-0.406061) = 0.683673.
This question was raised and discussed in the forum of my companion site Wizard of Vegas .
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I had run a sim (not me this is on the site) of 8,522,945 million dice rolls. Here are those results:
1,000,000/shooters
682796/total points wins
count points wins % or more or less
594110 0 0.5941100000
241267 1 0.2412670000 0.4058900000 0.8353770000
97983 2 0.0979830000 0.1646230000 0.9333600000
39547 3 0.0395470000 0.0666400000 0.9729070000
16136 4 0.0161360000 0.0270930000 0.9890430000
6535 5 0.0065350000 0.0109570000 0.9955780000
2596 6 0.0025960000 0.0044220000 0.9981740000
1067 7 0.0010670000 0.0018260000 0.9992410000
425 8 0.0004250000 0.0007590000 0.9996660000
188 9 0.0001880000 0.0003340000 0.9998540000
91 10 0.0000910000 0.0001460000 0.9999450000
55 11+ 0.0000550000 0.0000550000 1.0000000000
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
If I am reading this right based on 1 million shooters 55 times a shooter hit 11 or more points?
This seems like a much more realistic number.
March 8th, 2014 at 11:56:27 AM
permalink
The above chart can be found here:
https://wizardofvegas.com/forum/questions-and-answers/gambling/3146-average-number-of-points-hit-per-shooter-in-craps/#post33406
https://wizardofvegas.com/forum/questions-and-answers/gambling/3146-average-number-of-points-hit-per-shooter-in-craps/#post33406
March 8th, 2014 at 12:01:51 PM
permalink
59.39% shooter will not hit his point.
40.6% shooter will hit 1 or more points
16.1% shooter will hit 2 or more points
6.66% shooter will hit 3 or more points
If I take the opposite:
40.61% shooter will his his point
59.4% shooter will not hit 1 or more points
83.9% shooter will not hit 2 or more points
93.34% shooter will not hit 3 or more points
40.6% shooter will hit 1 or more points
16.1% shooter will hit 2 or more points
6.66% shooter will hit 3 or more points
If I take the opposite:
40.61% shooter will his his point
59.4% shooter will not hit 1 or more points
83.9% shooter will not hit 2 or more points
93.34% shooter will not hit 3 or more points
March 9th, 2014 at 6:19:22 PM
permalink
Quote: vegasrvpTo me the most important part is what you are considering a loss vs what I am considering a loss.
agreed
I went by what you posted earlier
"The loss moves you up the system and a win triggers a double up on he next roll."
my bet progression I used
bet # unit bet
1 1
2 1
3 1
4 2
5 2
6 4
7 4
8 8
9 8
10 16
11 16
12 32
13 32
14 64
15 64
Bet#1Quote: vegasrvpRoll example:
point come out roll is 6
Rolls of 2,5,9,8,8,5,4,11,12,6 winner means lose bet 1 move to next level
1
-1 net total
bet#2Quote: vegasrvppoint come out roll is 7
Lose bet 1
move to next level
1
-1 (-2 total)
bet#3Quote: vegasrvppoint come out roll is 11
lose bet 1
move to next level
1
-1 (-3 total)
bet#4Quote: vegasrvppoint come out roll is 5
rolls of 4,8,9,3,8,6,6,5 pint winner
lose bet 2
move to next level
2
-2 (-5 total)
Quote: vegasrvppoint come out roll is 3
winner win bet 2
move to next level double 2 (4)
*** Here I think you may not be following the rule below***
"The loss moves you up the system and a win triggers a double up on he next roll."
Only move to next level or bet after a loss
after a win double your last bet (parlay bet)
bet#5
2
+2 (-3 total)
*still at bet#5 (a win (last roll) triggers a double up on he next roll)
*unit bet = 4 (the double up or parlay bet)
I agree except I was on bet#5Quote: vegasrvppoint come out roll is 9
rolls of 4,6,5,10,3,5,2,7 out
winner of 8 units (less bets of 1,1,1,2 = 8-7=+1 unit for session)
Session complete move back to beginning
+4 (1 unit gain)
start over
it looks like I followed your rules perfectlyQuote: vegasrvpIs this what you thought? Also is this more clear?
the only event that you did not take into consideration is what happens after you make the 2nd and last 64unit bet and lose and you have, say, 84 units left?
I would just make another 64 unit - the max bet as I do not have enough to go to a 128 unit bet and that might be over the table limit too ($10 table max bet of $1000) and not just start over as that would give the lowest chance of getting back up and hitting my target I set at 510 units and dinner and dancing.
setup WinCraps and use my code and play your system
the average number of rolls to win or lose is about 1200
1700 on a win
800 on a loss
when you think on how a system can win or lose you need to consider every possible sequence of events
this is where a simulation comes in handy
how often do you think you should double a 255 starting bankroll?
It can never be greater than 50%
Sally
I Heart Vi Hart
March 10th, 2014 at 9:55:07 AM
permalink
Something just doesn't sit right in the over all numbers that are being thrown around.
I am in full agreement that long term this cannot and will not work, however, if there is a 59% chance that when a point is established I will be a winner playing the don't side.
How do I calculate hitting back to back don't winners? I'm guessing it is in the 34-35% range? This is eliminating both the 7/11 and 2/3 on the come out roll.
What I think is we may be looking at this backwards.
What are the odds of hitting 15 points out of 29 points established? (If we hit 15 points and go with the max rolls we would also hit 14 7outs in that same time)
Once we know that we could be calculate:
15 of 28
15 of 27
15 of 26 ect....thru 15 of 17.
Again.....over 1 million rolls this will bust like any other system based on the odds.
But, to go to a casino and win 10 units, bounce around tables and have some fun, I think you could do this for a good amount of time without a bust of -255 units. Can you hit 10 units 25+ times without a bust more then not.....who knows. Math probably says no and sitting for 1 million consecutive rolls will probably prove that conclusively. I personally do not have 50 hours a month for 10+ years to work out that kinda proof nor do I want to.
It is fun to play with the ideas though.
I am in full agreement that long term this cannot and will not work, however, if there is a 59% chance that when a point is established I will be a winner playing the don't side.
How do I calculate hitting back to back don't winners? I'm guessing it is in the 34-35% range? This is eliminating both the 7/11 and 2/3 on the come out roll.
What I think is we may be looking at this backwards.
What are the odds of hitting 15 points out of 29 points established? (If we hit 15 points and go with the max rolls we would also hit 14 7outs in that same time)
Once we know that we could be calculate:
15 of 28
15 of 27
15 of 26 ect....thru 15 of 17.
Again.....over 1 million rolls this will bust like any other system based on the odds.
But, to go to a casino and win 10 units, bounce around tables and have some fun, I think you could do this for a good amount of time without a bust of -255 units. Can you hit 10 units 25+ times without a bust more then not.....who knows. Math probably says no and sitting for 1 million consecutive rolls will probably prove that conclusively. I personally do not have 50 hours a month for 10+ years to work out that kinda proof nor do I want to.
It is fun to play with the ideas though.
March 10th, 2014 at 5:08:15 PM
permalink
why are you only looking at how the don't pass wins once a point is established? what is that fixation all about? 2 wins will never cancel out a 7/11 on the come out roll.Quote: vegasrvpSomething just doesn't sit right in the over all numbers that are being thrown around.
I am in full agreement that long term this cannot and will not work, however, if there is a 59% chance that when a point is established I will be a winner playing the don't side.
How do I calculate hitting back to back don't winners? I'm guessing it is in the 34-35% range? This is eliminating both the 7/11 and 2/3 on the come out roll.
What I think is we may be looking at this backwards.
What are the odds of hitting 15 points out of 29 points established? (If we hit 15 points and go with the max rolls we would also hit 14 7outs in that same time)
Once we know that we could be calculate:
15 of 28
15 of 27
15 of 26 ect....thru 15 of 17.
Again.....over 1 million rolls this will bust like any other system based on the odds.
you need to show better math to convince most that you are correct there.
look at every possible outcome and you will see why that 59% value is meaningless as I pointed out a few times before. I mean totally.
Here is data for the don't pass. The ways it wins, loses and pushes.
| Event | Freq. |
|---|---|
| Natural | 440 |
| Craps2,3 | 165 |
| Push 12 | 55 |
| 4 Made | 55 |
| 4 Not | 110 |
| 5 Made | 88 |
| 5 Not | 132 |
| 6 Made | 125 |
| 6 Not | 150 |
| 8 Made | 125 |
| 8 Not | 150 |
| 9 Made | 88 |
| 9 Not | 132 |
| 10 Made | 55 |
| 10 Not | 110 |
| Totals - | 1980 |
we add the events up and get this data
| event | prob |
|---|---|
| Natural | 0.222222222 |
| Craps2,3 | 0.083333333 |
| Push 12 | 0.027777778 |
| lose on point | 536 |
| win on point | 784 |
| lose on point | 0.270707071 |
| win on point | 0.395959596 |
| total | 1 |
| prob win | 0.479292929 |
| prob push | 0.027777778 |
| prob loss | 0.492929293 |
| prob win no push | 0.492987013 |
| prob loss no push | 0.507012987 |
If you use a 255 unit bankroll and want to win 10 units and quit playing and starting with a new 255unit bankroll at a future time your chance of winning is just under 96.2% (255/265)Quote: vegasrvpBut, to go to a casino and win 10 units, bounce around tables and have some fun,
I think you could do this for a good amount of time without a bust of -255 units.
I simulated this (you can do the same with WinCraps and my code) and it come in at 95.8% to win 1 session 1 time.
Now you want to win 25 times in a row to win 250 units
try 26 times in a row so a loss will only wipe out your total winnings
95.8%^26 = ?
That is your chance to win 26 sessions in a row without busting out your 255 bankroll
not impressive enough?
just playing with the 255 bankroll and trying to double while never using any of the winnings you have accumulated is about 45% success from my earlier simulation. 4 out of 9 or 1 out of 3? tough choice!
you should know now. But I think you must prove this to yourself.Quote: vegasrvpCan you hit 10 units 25+ times without a bust more then not.....who knows. Math probably says no
your current system wins on a first win or needs 2 wins in a row to win and start the progression over.
sometimes (55%) it can not do that with a 255 unit bankroll
maybe you should risk more to lose and win a few more times.
so true.Quote: vegasrvpIt is fun to play with the ideas though
and no fun being bummed out from the results from your ideas played many times
Have fun
see you in Las Vegas at the end of this month!
Sally
I Heart Vi Hart
March 16th, 2014 at 8:00:47 AM
permalink
Wanna mess with some new stuff?
Can I ask you to run another SIM?
I want to see a Sim on the don't pass and the don't come.
Initial bet 1 unit on the don't pass. (2x3x4)
5 base = 12 odds on 6/8
5 base = 15 odds on 5/9
5 base = 20 odds on 4/10
7, 11, 2, 3 ,12 just rebet
Once point is established use same betting strategy with up to four don't come wagers with same odds
Upon 7 out start over
If any or all don't come wagers lose we do not exceed a total of 4 don't comes per one 7 out.
I hope this makes some sense and if you have any need for clarification please ask.
Can I ask you to run another SIM?
I want to see a Sim on the don't pass and the don't come.
Initial bet 1 unit on the don't pass. (2x3x4)
5 base = 12 odds on 6/8
5 base = 15 odds on 5/9
5 base = 20 odds on 4/10
7, 11, 2, 3 ,12 just rebet
Once point is established use same betting strategy with up to four don't come wagers with same odds
Upon 7 out start over
If any or all don't come wagers lose we do not exceed a total of 4 don't comes per one 7 out.
I hope this makes some sense and if you have any need for clarification please ask.
March 16th, 2014 at 8:22:47 PM
permalink
Quote: vegasrvpWanna mess with some new stuff?
Can I ask you to run another SIM?
I want to see a Sim on the don't pass and the don't come.
Initial bet 1 unit on the don't pass. (2x3x4)
5 base = 12 odds on 6/8
5 base = 15 odds on 5/9
5 base = 20 odds on 4/10
7, 11, 2, 3 ,12 just rebet
Once point is established use same betting strategy with up to four don't come wagers with same odds
Upon 7 out start over
If any or all don't come wagers lose we do not exceed a total of 4 don't comes per one 7 out.
I hope this makes some sense and if you have any need for clarification please ask.
Those bets are straight 2X odds.
March 17th, 2014 at 12:49:24 PM
permalink
You're right:
I would like to know about starting with 200 units and how many times you will bust out vs doubling your 200?
I would like to know about starting with 200 units and how many times you will bust out vs doubling your 200?
March 18th, 2014 at 12:36:49 PM
permalink
do you mean a $200 bankroll or a $1000 bankrollQuote: vegasrvpI would like to know about starting with 200 units and how many times you will bust out vs doubling your 200?
You are flat betting at $5 (before odds) so $200 = 40 unit bankroll
$1000 = 200 unit bankroll
easier to double 40 units than 200 units
45% vs 37%
(this assumes that as the bankroll grows you do not take any away until you have hit your target bankroll. if you do your risk of ruin goes up and up and up)
now you are interested in don't come losing at most 4 times with odds by one shooter
but you do not count the number of times you lose the don't pass with odds? this could get messy when a "hot" shooter
starts out like this
7,11,7,4,4,6,11,6,8,3,8
you now have lost 3 dpass bets with odds and have 3 dcome bets with odds
you are not at all concerned about the hot shooter wiping out multiple dpass with odds bets?
maybe remove all the dcome bets with odds and chicken out. This shooter is causing you to lose too much.
got to feel better now, but
next roll 7 win
lost another dpass but won 3 dcomes with odds, oh no
still a loss to show for from one hot shooter
the code I used for WinCraps is a simple adjustment to the popular "risk of ruin" file that is free from the WC site
maybe you should get WinCraps and run these yourself
that way you can play with max 3 bets lost, then max 2 bets lost, then max4 bets lost with odds for both dpass-dcome
and as many combination of systems as you can think of
Sally
I Heart Vi Hart
March 18th, 2014 at 6:59:32 PM
permalink
The 7/11 on the don't line, and the don't come are just played as they do not exist.
The don't line initial bet is also counted as one of the four potential losses in a session so I guess I worded it wrong. It would be a max of 3 don't come bets with double odds along with the don't line initial come out.
I am looking to double 200 units so on a flat bet of $5 that would be $1000.
I have no doubt that there will be occasional losses. The max loss per shooter would be $90 with a flat $5 bet.
Example: Point 10 with $20 odds. Don't come 9 with $15 odds, Don't come 4 with $20 odds and Don't come 5 with $15.
$20+$20+$15+$15+$5base (4) = $90.
This is the max.
If I take the total units down to 100 vs 200 and with the don't come max at three will this change a lot in my favor.
On more thing. If I have a come out roll of 9 followed by a 4 then followed by another 9 and finally a 8 there will be no more don't come wagers as the four bets have posted. It is 4 total don't / don't come wager not four that actually go up.
Example:
5 point followed by 6, 9 6, 8,6,10,7out will be a winner on the 5, 9 and second 6 and a loss on the first 6.
5= winner of $15 (5 base plus 15 odds)
6 = loss of $17 (5 base plus 12 odds)
9=winner of $15 (5 base plus 15 odds)
6=winner of $15 (5 base plus 12 odds)
Total win = $28 (4 total bets with 3 wins and 1 loss)
YOU SAID:
now you are interested in don't come losing at most 4 times with odds by one shooter
but you do not count the number of times you lose the don't pass with odds? this could get messy when a "hot" shooter
starts out like this
7,11,7,4,4,6,11,6,8,3,8
7= -5
11= -5
7= -5
4 = don't point with 20 odds
4 = -25 (LOSS 1)
6 = don't come point
11= -5
8= don't come point
3= +5
8= -17 (LOSS 2)
if 7 comes now I lose another 5 for don't come and win the 6 for =15
total for shooter = -47 or just under 10 units
I agree this is a bad scenario but a 10 unit swing is not the end of the world.
I hope this clarifies a little.
Thanks,
Adam
The don't line initial bet is also counted as one of the four potential losses in a session so I guess I worded it wrong. It would be a max of 3 don't come bets with double odds along with the don't line initial come out.
I am looking to double 200 units so on a flat bet of $5 that would be $1000.
I have no doubt that there will be occasional losses. The max loss per shooter would be $90 with a flat $5 bet.
Example: Point 10 with $20 odds. Don't come 9 with $15 odds, Don't come 4 with $20 odds and Don't come 5 with $15.
$20+$20+$15+$15+$5base (4) = $90.
This is the max.
If I take the total units down to 100 vs 200 and with the don't come max at three will this change a lot in my favor.
On more thing. If I have a come out roll of 9 followed by a 4 then followed by another 9 and finally a 8 there will be no more don't come wagers as the four bets have posted. It is 4 total don't / don't come wager not four that actually go up.
Example:
5 point followed by 6, 9 6, 8,6,10,7out will be a winner on the 5, 9 and second 6 and a loss on the first 6.
5= winner of $15 (5 base plus 15 odds)
6 = loss of $17 (5 base plus 12 odds)
9=winner of $15 (5 base plus 15 odds)
6=winner of $15 (5 base plus 12 odds)
Total win = $28 (4 total bets with 3 wins and 1 loss)
YOU SAID:
now you are interested in don't come losing at most 4 times with odds by one shooter
but you do not count the number of times you lose the don't pass with odds? this could get messy when a "hot" shooter
starts out like this
7,11,7,4,4,6,11,6,8,3,8
7= -5
11= -5
7= -5
4 = don't point with 20 odds
4 = -25 (LOSS 1)
6 = don't come point
11= -5
8= don't come point
3= +5
8= -17 (LOSS 2)
if 7 comes now I lose another 5 for don't come and win the 6 for =15
total for shooter = -47 or just under 10 units
I agree this is a bad scenario but a 10 unit swing is not the end of the world.
I hope this clarifies a little.
Thanks,
Adam
March 19th, 2014 at 9:36:44 AM
permalink
four potential losses per shooterQuote: vegasrvpThe 7/11 on the don't line, and the don't come are just played as they do not exist.
The don't line initial bet is also counted as one of the four potential losses in a session so I guess I worded it wrong. It would be a max of 3 don't come bets with double odds along with the don't line initial come out.
I am looking to double 200 units so on a flat bet of $5 that would be $1000.
so after 4 total odds bets are made are you finished betting for the current shooter's hand? or
do you wait until you see how many bets you actually win/lose before making any more bets?
9,4,9,7,8 would be 4 bets with odds made but a 7 winner on the come out roll
lost a DP9
won two bets with odds (DC4,DC9), lost a DP and have only a DP8 with odds
do you make another don't come?
Quote: vegasrvpIf I take the total units down to 100 vs 200 and with the don't come max at three will this change a lot in my favor.
it is always easier to double a smaller number of units than a larger number of units if the betting unit stays the same.
here is how I see this exampleQuote: vegasrvpOn more thing. If I have a come out roll of 9 followed by a 4 then followed by another 9 and finally a 8 there will be no more don't come wagers as the four bets have posted. It is 4 total don't / don't come wager not four that actually go up.
New game started
Beginning bankroll: $1000
------New shooter coming out----------
$5 bet on Don't Pass
Roll #1: 9 (5.4) from manual roll pad
Point established
$15 bet on Don't Pass Odds <<<<#1
$5 bet on Don't Come
Roll #2: 4 (3.1) from manual roll pad
$5 Don't Come bet moved to Don't Come 4
$20 bet on Don't Come 4 Odds <<<<#2
$5 bet on Don't Come
Roll #3: 9 (5.4) from manual roll pad
Pass (point rolled)
Don't Pass bet lost $5
Don't Pass Odds bet lost $15
$5 Don't Come bet moved to Don't Come 9
Bankroll decreased to $980 ($20 loss)
$15 bet on Don't Come 9 Odds <<<<#3
Roll #4: 8 (5.3) from manual roll pad
Point established
$12 bet on Don't Pass Odds <<<<#4 last bet made until 7outI do not agree you win $28.Quote: vegasrvpExample:
5 point followed by 6, 9 6, 8,6,10,7out will be a winner on the 5, 9 and second 6 and a loss on the first 6.
5= winner of $15 (5 base plus 15 odds)
6 = loss of $17 (5 base plus 12 odds)
9=winner of $15 (5 base plus 15 odds)
6=winner of $15 (5 base plus 12 odds)
Total win = $28 (4 total bets with 3 wins and 1 loss)
I see your example as this. You say you stop making don't come bets after 4 total odds bets are made
New game started
Beginning bankroll: $1000
------New shooter coming out----------
$5 bet on Don't Pass
Roll #1: 5 (4.1) from manual roll pad
Point established
$15 bet on Don't Pass Odds <<<<#1
$5 bet on Don't Come
Roll #2: 6 (4.2) from manual roll pad
$5 Don't Come bet moved to Don't Come 6
$12 bet on Don't Come 6 Odds <<<<#2
$5 bet on Don't Come
Roll #3: 9 (5.4) from manual roll pad
$5 Don't Come bet moved to Don't Come 9
$15 bet on Don't Come 9 Odds <<<<#3
$5 bet on Don't Come
Roll #4: 6 (4.2) from manual roll pad
Don't Come 6 bet lost $5
Don't Come 6 Odds bet lost $12
$5 Don't Come bet moved to Don't Come 6
$12 bet on Don't Come 6 Odds <<<<#4 and no more bets to make until 7out
Bankroll decreased to $983 ($17 loss)
Roll #5: 8 (5.3) from manual roll pad
Roll #6: 6 (4.2) from manual roll pad
Don't Come 6 bet lost $5
Don't Come 6 Odds bet lost $12
Bankroll decreased to $966 ($17 loss)
Roll #7: 10 (5.5) from manual roll pad
Roll #8: 7 (4.3) from manual roll pad
Miss (seven-out)
Don't Pass bet won $5
Don't Pass Odds bet won $10
Don't Come 9 bet won $5
Don't Come 9 Odds bet won $10
Bankroll increased to $996 ($30 gain)
------New shooter coming out----------Net $4 Loss on last shooter and not a $28 win
I show a loss of only $32Quote: vegasrvpYOU SAID:
now you are interested in don't come losing at most 4 times with odds by one shooter
but you do not count the number of times you lose the don't pass with odds? this could get messy when a "hot" shooter
starts out like this
7,11,7,4,4,6,11,6,8,3,8
7= -5
11= -5
7= -5
4 = don't point with 20 odds
4 = -25 (LOSS 1)
6 = don't come point
11= -5
8= don't come point
3= +5
8= -17 (LOSS 2)
if 7 comes now I lose another 5 for don't come and win the 6 for =15
total for shooter = -47 or just under 10 units
I agree this is a bad scenario but a 10 unit swing is not the end of the world.
New game started
Beginning bankroll: $1000
------New shooter coming out----------
$5 bet on Don't Pass
Roll #1: 7 (5.2) from manual roll pad
Pass (natural)
Don't Pass bet lost $5
Bankroll decreased to $995 ($5 loss)
Roll #2: 11 (6.5) from manual roll pad
Pass (natural)
Don't Pass bet lost $5
Bankroll decreased to $990 ($5 loss)
Roll #3: 7 (5.2) from manual roll pad
Pass (natural)
Don't Pass bet lost $5
Bankroll decreased to $985 ($5 loss)
Roll #4: 4 (3.1) from manual roll pad
Point established
$20 bet on Don't Pass Odds <<<<#1
$5 bet on Don't Come
Roll #5: 4 (3.1) from manual roll pad
Pass (point rolled)
Don't Pass bet lost $5
Don't Pass Odds bet lost $20
$5 Don't Come bet moved to Don't Come 4
Bankroll decreased to $960 ($25 loss)
$20 bet on Don't Come 4 Odds <<<<#2
Roll #6: 6 (4.2) from manual roll pad
Point established
$12 bet on Don't Pass Odds <<<<#3
$5 bet on Don't Come
Roll #7: 11 (6.5) from manual roll pad
Don't Come bet lost $5
Bankroll decreased to $955 ($5 loss)
Roll #8: 6 (4.2) from manual roll pad
Pass (point rolled)
Don't Pass bet lost $5
Don't Pass Odds bet lost $12
$5 Don't Come bet moved to Don't Come 6
Bankroll decreased to $938 ($17 loss)
$12 bet on Don't Come 6 Odds <<<<#4 no more bets until 7out
Roll #9: 8 (5.3) from manual roll pad
Point established
Roll #10: 3 (2.1) from manual roll pad
Roll #11: 8 (5.3) from manual roll pad
Pass (point rolled)
Roll #12: 7 (4.3) from manual roll pad
Pass (natural)
Don't Come 4 bet won $5
Don't Come 4 Odds bet won $10
Don't Come 6 bet won $5
Don't Come 6 Odds bet won $10
Bankroll increased to $968 ($30 gain)Sally
I Heart Vi Hart
March 19th, 2014 at 10:21:39 AM
permalink
First off Sally, can I tell you that this is fun. I love this stuff.
Now for the details.
There are 4 total odds bets made per shooter max. If they run us all the way off the board eliminating all our wagers we wait for the next shooter.
YOU:
9,4,9,7,8 would be 4 bets with odds made but a 7 winner on the come out roll
lost a DP9
won two bets with odds (DC4,DC9), lost a DP and have only a DP8 with odds
do you make another don't come?
In this case we would have 9 point (1), DC 4(2), 9 don't loser replace the 9 from the DC(3), 7 winner pay the DC's, 8 point on the come out(4) no more bets on this shooter.
Shorter answer is NO. LOL
YOU:
Net $4 Loss on last shooter and not a $28 win
You are correct.....I did the math in my head and missed the second 6.
YOU:
I show a loss of only $32
You are also correct. I didn't account for replacing the 4.
So with these rules and looking to double vs lose a 100 unit bank roll are we still at 45% ish?
Second question, if after a losing session (100 unit loss) we then used a 200 unit and double base with a goal to only achieve returning the original 100 units are those odds improved?
Thanks again and please let me know when I get annoying.
Now for the details.
There are 4 total odds bets made per shooter max. If they run us all the way off the board eliminating all our wagers we wait for the next shooter.
YOU:
9,4,9,7,8 would be 4 bets with odds made but a 7 winner on the come out roll
lost a DP9
won two bets with odds (DC4,DC9), lost a DP and have only a DP8 with odds
do you make another don't come?
In this case we would have 9 point (1), DC 4(2), 9 don't loser replace the 9 from the DC(3), 7 winner pay the DC's, 8 point on the come out(4) no more bets on this shooter.
Shorter answer is NO. LOL
YOU:
Net $4 Loss on last shooter and not a $28 win
You are correct.....I did the math in my head and missed the second 6.
YOU:
I show a loss of only $32
You are also correct. I didn't account for replacing the 4.
So with these rules and looking to double vs lose a 100 unit bank roll are we still at 45% ish?
Second question, if after a losing session (100 unit loss) we then used a 200 unit and double base with a goal to only achieve returning the original 100 units are those odds improved?
Thanks again and please let me know when I get annoying.
