i bring $1500 to the table.
lets say it's a great roll and the amount of chips on my rail is up +$2000. There's also $300 in total odds and $500 Place bets on the 6/8 each on the table.
I've exceeded my win goal of double my buy-in and the same shooter is still shooting.
i hate it when the 7 comes and wipes out all that $ on the table.
How to minimize the $ on the table when the 7 eventually comes?
Better question, should i bother minimizing the $ lost?
i don't know when the 7 will come. it might be the next roll, or it might be 20 #s from now.
Accept the fact that leaving lots of $ on the table after a hot roll is part of the game???
The alternative to regressing is to stop pressing and just let the existing bets stay and hopefully pay.
If only we knew which number would hit next. If only we knew when the devil would show.
Quote: 100xOddsi hate it when the 7 comes and wipes out all that $ on the table.
Well, I think we forget that we made the come bet and have a point to resolve; the bet has become less likely to win, and there we have maybe stacked up a bunch of that. What makes us forget is the free odds, which we think of in a positive way but are also supposed to lose most of the time [just paying better than even to make up for it]. I also hate the dramatic way the 7-out clears it all out, so many times just as it looked like we might be on our way to a nice win. But I think drama is all it is.
Yes.Quote: 100xOddsAccept the fact that leaving lots of $ on the table after a hot roll is part of the game???
A few years ago, my wife found me at the craps table. She knows enough to know which chips were mine based on position and saw over $400 get wiped out when the next roll was a 7. (I generally start each shooter with just $12 each on 6 and 8.)
She started to say something about how much money I just lost. I merely pointed to the full rail in front of me and she shut up real quick.
So, yeah, in craps, a big loss, at the end of a great shooter, is not merely part of the game, but in a bizarre sense, a desired part of the game. I.E. I'd love to have $400 working for EVERY shooter when they 7-out!
Quote: DJTeddyBearYes.
A few years ago, my wife found me at the craps table. She knows enough to know which chips were mine based on position and saw over $400 get wiped out when the next roll was a 7. (I generally start each shooter with just $12 each on 6 and 8.)
She started to say something about how much money I just lost. I merely pointed to the full rail in front of me and she shut up real quick.
So, yeah, in craps, a big loss, at the end of a great shooter, is not merely part of the game, but in a bizarre sense, a desired part of the game. I.E. I'd love to have $400 working for EVERY shooter when they 7-out!
I know the feeling... But I changed my tune when I found a little chart that I believe 7craps put up... It was about the tendency of the seven to show after certain amount of rolls. When you get to 20 plus rolls... The risk versus reward has flipped (think of it like a polar shift in science) back to the beginning...
1. If you for some reason have worked your way to 2400 across with 400 on each number, You would need at least 4 hits to recoup that. There is another place that this happens... It is when you have your initial bet!!! Alot if you might not agree with his but This means you have reached the end of a cyle. The amount of money on the table has went over the risk... Why not just take the 2k off the table and start with 400 on whatever number you see fit... You will still have bets out
Quote: TheWolf713If you for some reason have worked your way to 2400 across with 400 on each number, You would need at least 4 hits to recoup that.
Hopefully you've already won more than this, so you are not really recouping it - just hoping for an even bigger win.
Sometimes when my bankroll is in decent shape I play very aggressively - pressing early and often hoping I've got good timing and hit some long rolls. I realized I was pressing too aggressively and on rolls where most numbers hit 2 or 3 times I was leaving almost as much on the table as I'd added on the rail. it was a nice win, but too much of a loss in my mind. I came up with a couple of tweaks to my strategy. One is to skip the press every so often. Another is a form of regression: stop making continuous come bets and when a number hits, replace it with a smaller place bet - so $10 + $50 odds on a six is replaced with a $30 place bet when it hits.
This is true at every point in the cycle. And if you ignore the advice to cut back, and instead win a little more and press a little more, this statement will be true again.Quote: TheWolf713You would need at least 4 hits to recoup that. There is another place that this happens... It is when you have your initial bet!!! A lot of you might not agree with this, but this means you have reached the end of a cycle.
My advise is once you get over the initial hump, keep going. Just don't get crazy. Wanna be conservative? Fine. Take a few without pressing.
Quote: DJTeddyBearThis is true at every point in the cycle. And if you ignore the advice to cut back, and instead win a little more and press a little more, this statement will be true again.
My advise is once you get over the initial hump, keep going. Just don't get crazy. Wanna be conservative? Fine. Take a few without pressing.
I have to agree with DJ on this one.
If you don't press and the shooter hits 4 of your numbers, you just covered everything that was on the table (rough estimate). If the shooter hits 5 of your numbers, you will have 'lost' bigger gains. I have noted this before, but for my style of play, I need to win big on those big rolls, or I will most likely have a losing session.
However, if your style is to grind out a win, then money management and minimizing chip loss to a 7 out is important.
If you're looking for a major win, you leave it in play and keep pressing at times.
If you're looking to have a winning session every time, then when you get ahead on a shooter, play so that you cannot lose money on that shooter.
What you can't do is mix styles. A grinder playing for the big score, or 'the go big go home' player trying to grind all of a sudden usually doesn't work. It will leave you regretting many of your decisions later.
Quote: AlanMendelsonIf I ever get lucky enough to have multiple chips (bets) on the place numbers, I would use the strategy of regressing back to the table minimum and then slowly press the numbers up again. I have the plan. I just need a chance to put it into action.
I used to feel the same way, but then I got paid a few times with $100+ on a number, and there is just something so sweet about putting black and green chips in the rack when one of your numbers rolls. I think I may have tried regressing one time, but all I could do was count the number of box numbers that came up AFTER I regressed, and decided I had given up a few hundred in potential wins.
As has been said so many times......... the only way to play craps successfully is to know what the next roll will be.
Quote: 100xOdds3/4/5x odds, $10min
i bring $1500 to the table.
lets say it's a great roll and the amount of chips on my rail is up +$2000. There's also $300 in total odds and $500 Place bets on the 6/8 each on the table. I've exceeded my win goal of double my buy-in and the same shooter is still shooting. i hate it when the 7 comes and wipes out all that $ on the table.
I can't believe what you've just said. Everyone else has kindly suggested minimizing. Maybe I misunderstand your situation. You say your rail is "up +$2000." Does that mean that's in addition to your $1,500 buy-in? If so, you have $3,500 in the rack. And, you have $1300 on the table? You're foolish to make that $1300 bet. Your total value at that point is $4800. Color up. $4800 - 1500 = $3300 profit. What more can you want? Color up, go for a beer for an hr., then come back.
Maybe my math is way off & I misunderstand you completely, but to me, some of you guys get too greedy & of course, the 7 hits. Don't push your luck. The dice always take back what they give. Leave a session feeling good, if you can. FWIW.
not IQuote: 100xOddsi hate it when the 7 comes and wipes out all that $ on the table.
Make Lay bets only.
I do not hate it when the 7 rolls, any 7, out or winner
Lay bets have the highest winning probability at Craps for any one number bet
and are favored to win more than they lose the longer one makes them.
Alan M says playing craps is all about winning as I recall. Only winning matters.
does it matter about what KIND of winning?
I say how many times you win is good and not really how much you win, bet big to win big, do not play scared.
maybe I did not understand what he (AlanM) said, exactly.
We play short run sessions.
so IMO, make the individual bets that have the highest probability of winning.
Greater the 50%.
66.7% and 60% and 54.5%
anything less, you are gambling and
still playing scared
right?
screw the place6 or place8
it (yuk) wins at a rate of 5/11 (45.45%)
and that is ever so slightly better than
the sucker Field bet (yuk) that wins at a rate of 16/36 (44.44%)
not much of a difference between those two bets.
I love playing Craps scared
I love playing Craps
I love playing
I love
I
Quote: Sonny44I can't believe what you've just said. Everyone else has kindly suggested minimizing. Maybe I misunderstand your situation. You say your rail is "up +$2000." Does that mean that's in addition to your $1,500 buy-in? If so, you have $3,500 in the rack. And, you have $1300 on the table? You're foolish to make that $1300 bet. Your total value at that point is $4800. Color up. $4800 - 1500 = $3300 profit. What more can you want? Color up, go for a beer for an hr., then come back.
Maybe my math is way off & I misunderstand you completely, but to me, some of you guys get too greedy & of course, the 7 hits. Don't push your luck. The dice always take back what they give. Leave a session feeling good, if you can. FWIW.
yep 3500 in the rack plus $1300 on the table
the thing that stops me from picking everything up is that I cant pick up the flat bets.
I thought about just leaving the flat bets to dealer as tip, pick up everything else, walk to the cashier and not look back
Quote: 100xOddsyep 3500 in the rack plus $1300 on the table. The thing that stops me from picking everything up is that I cant pick up the flat bets. I thought about just leaving the flat bets to dealer as tip and pick up everything else.
A good idea. (I don't know what your flats amount to, but at least take down any odds. Probably better not to make the final bet in the first place.) "Take the money and run," as they say.
Quote:Long rolls: How to prevent lots of $ from sitting on the table when the 7 comes?
Simple answer.
Let it ride.
After a long roll you should have at least doubled your place bets and made some profit.
Let it ride all the way to max bet.
Long rolls don't happen all the time so take advantage of the opportunity.
There are some days when I have probably 1000 + in chips on the table, but when a 100/4 or 10 comes in and you press to make 400, it doesn't take long to get up to 1k in bets.
I don't like leaving all that money on the table either, but my only thought, if you are 20+ rolls for this shooter?
Maybe take down some of your odds bets, and move them to the Don't Come?
The contract bets are still playing, and at risk, but if the seven comes after a couple of rolls, the DC pays and minimizes the losses.
Otherwise, its hope for the best...
SFB
It was a $5 table, and the shooter made four passes (no fire bet, unfortunately) and I had the inside numbers pressed up to $25, $30, $30, $25 with $5 on both the 4 and ten.
He rolled another repeater point, so I regressed to the table minimum $27 across with double odds. He hit that point (now five passes, but still no fire) and he established another repeater point. I removed all my bets and said "just make this pass and get the fire." (I had $5 on the fire, which was the maximum). He rolled two more box numbers and it was over.
The shooter colored up and left with about $2600 in all, but he left on the table what appeared to be another $900. (He was a green chip player from the start.)
If you can't mentally stand the loss then you need win limits.
Quote: SFB100X:
I don't like leaving all that money on the table either, but my only thought, if you are 20+ rolls for this shooter?
Maybe take down some of your odds bets, and move them to the Don't Come?
The contract bets are still playing, and at risk, but if the seven comes after a couple of rolls, the DC pays and minimizes the losses.
Otherwise, its hope for the best...
SFB
Let the fire bet control what and when to bet on the dark side. if I'm already up in chips from my place bets and shooter is on his 4th point, start hedging and lay that 120 against the 4th point or even wait and lay 600 on the 5th or even 2000 against the 6th.
DC betting is not a good idea, but laying the point in fact will ensure a profit from both sides.
Quote: kenarmanYou can never make big money unless you are willing to take the big hit on the seven out. I usually play a $5 table and buy in with no more than $200 and often only $100. The thrill of filling my rack with green and black chips overides the fact that the 7 out might have cost me the few grand that was on the table.
If you can't mentally stand the loss then you need win limits.
If you can't mentally stand the loss then you need win limits.
Amen to that.
Quote: ontariodealeryou got to leave money to make money. A couple of weeks ago from $450 start I was down to 46 bucks playing 66 and 44 inside.....some old bag got the dice and i said to hell with it, 44 inside and press like crazy.....well doesn't she go off for 20 minutes, i had $1800 in my rack and $700 on the table when the seven came....was I suppoed to be unhappy???
I ran a wincraps simulation with a Inside bet file, using multiple methods including:
Press 1 unit, Double, and Parley. After thousands of sessions run on hyperdrive, all methods failed.
Re-did simulations using a 1 point regress (120 inside, after 1 hit, take bets down to 44 inside using Press 1 unit) huge change in results and positive outcome. (Minimum $500 bank roll needed for this type of betting)
Here is a good bet to introduce anyone to early pressing with slight hedging and last come get some. Great for the long roll shooters. Starting recommended bankroll $300 - $500. Come bets will limit your aggressive styles and control your chip stacks.
wincraps classic file:
When . . .
Initializing Auto-Bet
then . . .
Name Chip-Stack # 1 as "Number of rolls after point established"
Set Auto-Handle Winning Bets to "Same Bet - Take Winnings"
While . . .
A point is established on any number
then . . .
Add $ 1 to Chip-Stack # 1
else . . .
Bet $ 0 on Chip-Stack # 1
While . . .
Next roll is a come-out roll
then . . .
Bet $ 5 on Pass Line
Bet $ 5 on Field
When . . .
A point is established on any number
then . . .
Set Auto-Take Full Odds to True
Bet $ 15 on all Place bets
Bet $ 0 on Place (shooter's point)
Bet $ 5 on Come
When . . .
On each roll
then . . .
Bet $ 5 on Come
Bet $ 5 on Field
"Game > Configure > Probabilities > Unlock all cells (Change the 7 to 10.000) and Check "Use the probabilities..." to give you a more live table feel for the dice.
"Game > Configure > Bankroll > Start bankroll with 0 and Check "Allow negative..."
I've also tested a more advanced version in the wincraps pro with the help of 7craps to allow a slightly aggressive progression as your chip stack grows taking this simple betting style into 7 figure incomes running a full "1 year simulation"
wincraps pro file available for those interested.
Quote: 100xOdds3/4/5x odds, $10min
i bring $1500 to the table.
lets say it's a great roll and the amount of chips on my rail is up +$2000. There's also $300 in total odds and $500 Place bets on the 6/8 each on the table.
I've exceeded my win goal of double my buy-in and the same shooter is still shooting.
i hate it when the 7 comes and wipes out all that $ on the table.
How to minimize the $ on the table when the 7 eventually comes?
Better question, should i bother minimizing the $ lost?
i don't know when the 7 will come. it might be the next roll, or it might be 20 #s from now.
Accept the fact that leaving lots of $ on the table after a hot roll is part of the game???
This kind of choice is faced constantly in playing craps; only the dollar magnitudes of the numbers are different.
Suppose you bet $100 on pass, get a point of 8, bet $500 on odds and win the bet. You've won $700. Do you take the money and run? Depends on how much you value that $700, or how great it will feel to leave the table a winner, as all the money-management gurus advise. Your chance of winning more is the same as it was before that first bet. If you bet again (same flat bet, point and odds) and lose, you lost $600 of your $700, but if you win you've won $1400. Is the lure of another $700 enough to overcome the fear of losing $600 of what you've won?
In 100xOdds' situation, is the difference between the current $$ in the rail and that amount minus $800 more important than the chance to win some more? Go back one shooter; why did you decide to keep betting then?
Suppose you've got money on the inside numbers. You can take them down. But you just won one of those bets. What if you had pulled your bets before that? You would have missed out. I'm sure we've all had the experience of cashing out, or pulling down bets and then seeing that that/those bet(s) would have won. Or the opposite; you leave the money out there and, "seven out, line away!".
BTW, the seven does NOT become any more or less likely after different numbers of rolls without one. The probability of x rolls before a 7 only applies before the series begins.
At some point, the money in your rail is more important than the money you might win. Only one person (or one's wife >:-) can make that decision.
Telling someone he/she "should" leave the money out there until the seven out, or he/she "should" regress or pull the bets down is kind of arrogant, isn't it? There's no one "should" for everyone. The important thing is to understand what will happen either way, then decide for yourself.
This is the same kind of decision as whether to flat bet, progress or regress.
Cheers,
Alan Shank
1) not enough bankroll left to make the next bet
2) reached the win goal
3) reached the number of resolved bets
It only handles relatively simple situations, pass or don't pass with various odds multiples, a single place bet, field bets, etc., and only constant bet amounts.
An interesting feature, which is relevant to this thread, is that it can set a further win goal instead of stopping when the original win goal is reached. You input the percentage of the win goal you are willing to risk. It saves the rest and continues to play until you have lost the amount risked or you have reached the 2nd win goal. It keeps doing this until you "bust", i.e. lose the amount you are risking. An example will make this more clear.
bankroll $500
win goal $250
percentage to risk 20%
maximum number of bets 60
$5 pass, 5x odds
With the "debug" variable set, it outputs data whenever a win goal is reached.
Reached win goal of $ 250.0000, number 1 bankroll now $763.0000
New win goal is $885.0000, floor $713.0000
Here, the player "overshot" the win goal, which often happens when taking odds. Now, the new win goal is the current bankroll plus 1/2 of the original win goal. 20% of $250 is $50, so we will only risk that much, making the "floor" $713. This means that if the bankroll gets down to or below the floor, the session is over. Only risking 20% of the win goal means you don't have much to continue playing, but if you keep winning that doesn't matter.
Reached win goal of $ 250.0000, number 1 bankroll now $776.0000
New win goal is $900.0000, floor $726.0000
Reached win goal of $ 400.0000, number 2 bankroll now $910.0000
New win goal is $1035.0000, floor $860.0000
Now, the player has reached (and overshot) the 2nd win goal. The new win goal is another $125, with the "floor" $50 below the current bankroll, or $860.
In this trial of this simulation, the player did not reach the $1035, so the session ended.
Reached win goal of $ 250.0000, number 1 bankroll now $751.0000
New win goal is $875.0000, floor $701.0000
Reached win goal of $ 375.0000, number 2 bankroll now $915.0000
New win goal is $1040.0000, floor $865.0000
Reached win goal of $ 540.0000, number 3 bankroll now $1058.0000
New win goal is $1180.0000, floor $1008.0000
That time, the player made the 2nd win goal and went on to a 3rd, another $125 up with a "floor" $50 below current. This can go on indefinitely, of course. Here's one where the player got to #4:
Reached win goal of $ 250.0000, number 1 bankroll now $793.0000
New win goal is $915.0000, floor $743.0000
Reached win goal of $ 415.0000, number 2 bankroll now $945.0000
New win goal is $1070.0000, floor $895.0000
Reached win goal of $ 570.0000, number 3 bankroll now $1071.0000
New win goal is $1195.0000, floor $1021.0000
Reached win goal of $ 695.0000, number 4 bankroll now $1195.0000
New win goal is $1320.0000, floor $1145.0000
For that run of just 1000 sessions, the most win goals set were five (four reached).
The program keeps track of the ending bankroll for all the sessions that reached the first win goal. In a run of 100,000 sessions, same data, the win goal was reached 25.2% of the time. The average net win for these sessions was $266.11, with a standard deviation of $94.73, with six the most win goals reached. Since the win goal is often "overshot", the $266 figure probably means that there was a small net loss, on average, after the first win goal, but a lot of variation.
You can also think about it this way: having reached the goal, you are now playing with between $50 and $100, depending on by how much you "overshot" the first win goal, trying to win $125. When I simulated that, the $50 was busted 68.6% of the time, the $125 reached 23%.
Every time you get to one of these goals, the future expectation is negative, just as it always is, but you've "locked away" most of your winnings each time.
BTW, the program never quits on a loss, and I don't, either. I think that was one of the "Dice Doctor's" maxims: "Never quit after a win." So, if the trial has reached the maximum number of bets, it keeps going until a bet is lost.
Of course, you could fool around with the size of the future win goals. The program always add half of the original win goal to the current bankroll. I may modify this so that you can input a different fraction or percentage. This way, you could control the relative sizes of the new win goal and the amount to risk.
Cheers,
Alan Shank
now that I have your attention
hehe
I can?Quote: goatcabin<SNIP> Of course, you could fool around with the size of the future win goals.
I mean, in other words,
I like to fool around
It has been proven a number of times in the pastQuote: goatcabinThe program always add half of the original win goal to the current bankroll. I may modify this so that you can input a different fraction or percentage. This way, you could control the relative sizes of the new win goal and the amount to risk.
Cheers,
Alan Shank
that going past the win goal instead of hitting it exactly or as close as possible
actually decreases the probability of hitting that win goal
decrease is not good
SN Ethier paper on
IMPROVING ON BOLD PLAY AT CRAPS
is a fun read and has great craps math too
Sally
Quote: mustangsally
It has been proven a number of times in the past
that going past the win goal instead of hitting it exactly or as close as possible
actually decreases the probability of hitting that win goal
decrease is not good
SN Ethier paper on
The "overshots" are only because of the odds bets. IOW, you are ahead $240 (WG is $250), and you have $5 pass w/$25 odds on 4. When you win that bet, you have $275. When you are taking or laying odds, it's often not possible to hit a particular figure exactly.
Cheers,
Alan Shank
the choice should be either bet $10 pass no odds or $5 flat with $5 odds. I think the $10 flat would be the best (highest success probability)Quote: goatcabinThe "overshots" are only because of the odds bets. IOW, you are ahead $240 (WG is $250),
that is going way overQuote: goatcabinand you have $5 pass w/$25 odds on 4. When you win that bet, you have $275. When you are taking or laying odds, it's often not possible to hit a particular figure exactly.
Cheers,
Alan Shank
that is not good when it comes to hitting win goals
I have lots on craps win targets transition matrices about this
sometimes they are not intutive, the results that is
Sally
Quote: mustangsallythe choice should be either bet $10 pass no odds or $5 flat with $5 odds. I think the $10 flat would be the best (highest success probability)
that is going way over
that is not good when it comes to hitting win goals
I have lots on craps win targets transition matrices about this
sometimes they are not intutive, the results that is
Sally
The point of this program is not to maximize the probability of reaching a win goal; it's to examine the probability of reaching a win goal (or busting), given a particular bet, which is constant. In these runs, I was simulating $5 pass, 5x odds. In the situation above, you're asking, "How can I win exactly $10." As we have examined in other threads, the probability of reaching some win goal is most dependent on variance.
Cheers,
Alan Shank
did you give "this" program a name?Quote: goatcabinThe point of this program
maybe Rose 1, has a nice sound to it
yes, I figured out that partQuote: goatcabinis not to maximize the probability of reaching a win goal;
I would still like to know the highest probability of hitting a win goal, but that is just me, that is Sally
yes sirQuote: goatcabinit's to examine the probability of reaching a win goal (or busting), given a particular bet, which is constant.
very niceQuote: goatcabinIn these runs, I was simulating $5 pass, 5x odds.
well, I see it as I have $240 and I want (need) $250Quote: goatcabinIn the situation above, you're asking, "How can I win exactly $10."
so I ask myself
"Sally?"
yes
"what would give me the best chance to get $250 having just $240 (a girl's worst nightmare!)
and the answer I give is to bet $10 on the pass
no, $10 on the don't pass.
Oh, wait, the condition was pass line bets only
Damn, Sally says
Hmmm,Quote: goatcabinAs we have examined in other threads, the probability of reaching some win goal is most dependent on variance.
Cheers,
Alan Shank
I say it is Bold Play, meaning I want the best chance, not just a whim or superstition chance,
in other words
betting what it takes to hit the win goal on the very next bet, even if that means all I gots!
Yes, Mary Ann, I like you and Ginger
of course the odds bet for the pass and dpass change that as proven by SN Ethier
you two seem to look a like, except for the white hair, and are about the same age also
wow I say
Sally
why so many dups
Sally
I usually flat bet, and press by making come bets [or the DC if on that side]. Since this pressing is purely playing hunches, it doesnt work to try to make a Wincraps file to do it. I freely admit that playing hunches cannot be defended, except that I will say that there is a certain amount of action I want to put into play and that is how I like to do it. As long as I keep the amount of the action the same, this superstition IMO is harmless.
As far as the OP goes regarding that deadly build up of points to make, with the seven-sided sword hanging over them ... let me add that I have concluded that to limit one's action is just prudent in an obvious way for rightside play, but I've learned the hard way that the same holds for darkside play. You really need to limit your action either way, or pay the price [most times], on either side of things. This is intuitive for rightside play, counter-intuitive for darkside play [what with a number of points to make 'looking good'], yet true either way.
Quote: mustangsallydid you give "this" program a name?
maybe Rose 1, has a nice sound to it
Actually, it is called ruinodds, so named after I added the ability to do odds bets into it. I believe I got the basic structure from a Basic program somebody posted; can't remember whether this was in the old Usenet days, here, or on Craps Forum.
"As we have examined in other threads, the probability of reaching some win goal is most dependent on variance."
Quote: mustangsallyHmmm,
I say it is Bold Play, meaning I want the best chance, not just a whim or superstition chance,
in other words
betting what it takes to hit the win goal on the very next bet, even if that means all I gots!
Sally
Well, and that maximizes variance, right? The SD of one $250 pass bet is $249.98, of 25 $10 pass bets just $50. The more different outcomes, the less variance, all other things being equal.
The original intent of this program was to help people decide how much bankroll they needed to have a low probability of busting with a certain type of play. Over the years, I have added lots of other stuff, and it's gone from Basic (maybe even originally Fortran) to C to C++.
Cheers,
Alan Shank
Quote: goatcabinActually, it is called ruinodds, so named after I added the ability to do odds bets into it. I believe I got the basic structure from a Basic program somebody posted; can't remember whether this was in the old Usenet days, here, or on Craps Forum.
"As we have examined in other threads, the probability of reaching some win goal is most dependent on variance."
Well, and that maximizes variance, right? The SD of one $250 pass bet is $249.98, of 25 $10 pass bets just $50. The more different outcomes, the less variance, all other things being equal.
Just curious, but how do you calculate the standard deviation for one bet?
Quote: ConcinnityJust curious, but how do you calculate the standard deviation for one bet?
https://wizardofvegas.com/forum/gambling/craps/15844-come-bets-are-a-3-hedge-against-the-7/2/#post428645
Quote: goatcabinhttps://wizardofvegas.com/forum/gambling/craps/15844-come-bets-are-a-3-hedge-against-the-7/2/#post428645
I read what you posted at the above link. thank you (and disagree with your explanations as to reasons, but I don't work as a statistician, so perhaps one of the statisticians on the list can address those issues -- for example, we don't square and then take the square root to eliminate the minus sign -- really, we'd find using absolute value enormously easier). I suppose you didn't understand my question. My fault. Sorry. I'll rephrase.
If you define standard deviation as the square root of the variance, then how can you have a variance with only one sample (bet)? And therefore, if you have no variance, then how can you have a standard deviation?
Quote: Concinnity
If you define standard deviation as the square root of the variance, then how can you have a variance with only one sample (bet)? And therefore, if you have no variance, then how can you have a standard deviation?
Well, any bet has more than one outcome; the variance measure the differences from the ev of those outcomes, weighted by their probabilities.
I illustrated that with the 12.
The SD of one bet is not that helpful, but when you make lots of bets, it (increased by the square root of the number of bets), shows you the likely distribution of outcomes.
Cheers,
Alan Shank
Quote: goatcabinWell, any bet has more than one outcome; the variance measure the differences from the ev of those outcomes, weighted by their probabilities.
I illustrated that with the 12.
I saw your illustration using the 12. While I understand it, you've also totally lost me. :) When not using any actual samples (as in: someone threw the dice, made the bets, etc.), the "difference" from the expected value must always equal zero. The expected value doesn't change, just like the probability of a seven occurring doesn't change. Which you know, of course. In other worse, I have a suspicion you've create a tautology which reduces back to the simple probabilities involved.
You've also totally lost me on what you mean by weighting the difference in expected value by their probabilities. Expected values already have a probability associated with them. After all, we use that to calculate them. See my comments about the tautology.
Now, I know we want to investigate the variability of a particular betting system in terms of bankroll (duh!). In such a case we can *never* figure that out, precisely. Ever. (Well, aside from trivial cases which, I think, wouldn't interest anyone.) Because it depends on totally random chance over a significant amount of time (not too many of us want to make one bet and then leave the table. or something equally simple). However, to do this properly we can assign a nice confidence interval and then figure out what sort of bankroll a bettor using such-and-such a system would require, within that confidence interval. For example, "if you use the X betting system, then you have a 95% chance of not running out of money within such-and-such number of rolls/bets." (N.B.: quite a different statement than one involving only simple probabilities, such as "how many rolls will occur, on average, before I hit that feature bet?")
But I would not call that variance.
In fact, I'd go so far as to say that we should only use the statistical tools of variance and standard deviation for things that have already happened (actual samples).
(It also wouldn't hurt to understand why we use root-mean-square to emphasize the impact of outliers, but I digress.)
Quote: goatcabinThe SD of one bet is not that helpful, but when you make lots of bets, it (increased by the square root of the number of bets), shows you the likely distribution of outcomes.
Yes, I know that. I would go so far as to say that the standard deviation of one bet seems a lot worse than helpful.
In fact, unless we set up a proper confidence interval for a betting system, then I don't see why we should bother with standard deviation at all. Presuming, of course, that we don't run a casino (in that case I would want really good analytics for lots of reasons).
By the way, for some reason no one uses the term "variance" when they win a hell of a lot. :) I guess it only counts when you lose. :)
Quote: ConcinnityI saw your illustration using the 12. While I understand it, you've also totally lost me. :) When not using any actual samples (as in: someone threw the dice, made the bets, etc.), the "difference" from the expected value must always equal zero. The expected value doesn't change, just like the probability of a seven occurring doesn't change. Which you know, of course. In other worse, I have a suspicion you've create a tautology which reduces back to the simple probabilities involved.
No, the difference from the ev is for each possible outcome, as shown in that example.
Quote: ConcinnityYou've also totally lost me on what you mean by weighting the difference in expected value by their probabilities. Expected values already have a probability associated with them. After all, we use that to calculate them. See my comments about the tautology.
Once again, it's the outcomes (and their differences from the ev) that are weighted by their probabilities.
Quote: ConcinnityNow, I know we want to investigate the variability of a particular betting system in terms of bankroll (duh!). In such a case we can *never* figure that out, precisely. Ever. (Well, aside from trivial cases which, I think, wouldn't interest anyone.) Because it depends on totally random chance over a significant amount of time (not too many of us want to make one bet and then leave the table. or something equally simple). However, to do this properly we can assign a nice confidence interval and then figure out what sort of bankroll a bettor using such-and-such a system would require, within that confidence interval. For example, "if you use the X betting system, then you have a 95% chance of not running out of money within such-and-such number of rolls/bets." (N.B.: quite a different statement than one involving only simple probabilities, such as "how many rolls will occur, on average, before I hit that feature bet?")
That's exactly what the standard deviation is good for. Suppose you are going to play $5 pass with 3, 4, 5x odds for 60 bets. The ev is about -$4 and the SD is $190. 95% chance corresponds to about 1.6 standard deviations (on one tail); 1.6 x $190 is $304, so $300-$325 in starting bankroll would give you about a 95% chance of your bankroll lasting 6 bets.
Quote: ConcinnityIn fact, unless we set up a proper confidence interval for a betting system, then I don't see why we should bother with standard deviation at all. Presuming, of course, that we don't run a casino (in that case I would want really good analytics for lots of reasons).
But the whole concept of confidence intervals is based on standard deviation!
Cheers,
Alan Shank
Quote: goatcabin
That's exactly what the standard deviation is good for. Suppose you are going to play $5 pass with 3, 4, 5x odds for 60 bets. The ev is about -$4 and the SD is $190. 95% chance corresponds to about 1.6 standard deviations (on one tail); 1.6 x $190 is $304, so $300-$325 in starting bankroll would give you about a 95% chance of your bankroll lasting 60 bets.
I have to backtrack a bit on that number, because the calculation assumes all 60 bets are resolved. A session with a larger bankroll that ended down $305 could have been down farther than that and come back. Still, it's a "quick-and-dirty", "back-of-the-cocktail-napkin" way to estimate it. More accurately, simulate 10 or 20,000 sessions starting with a target bankroll and see how many of them bust. This is easy to do in WinCraps.
Cheers,
Alan Shank
Don't put more money on the table than you're comfortable with.
Don't want to lose more than $200 to a 7 out?
Simple, stop placing more wagers once you have $200 on the table.
Quote: sc15There's a real simple answer to this:
Don't put more money on the table than you're comfortable with.
That is basically my only money-management principle. The rest is, as the Wizard says on his wizardofodds site, "mathematical voodoo".
Cheers,
Alan Shank
not many here ever thinking about variance as far as I (eye) can see (C).Quote: goatcabinSuppose you are going to play $5 pass with 3, 4, 5x odds for 60 bets.
The ev is about -$4 and the SD is $190.
95% chance corresponds to about 1.6 standard deviations (on one tail); 1.6 x $190 is $304, so $300-$325 in starting bankroll would give you about a 95% chance of your bankroll lasting 6 bets.
But the whole concept of confidence intervals is based on standard deviation!
Cheers,
Alan Shank
All the experts talk about is the ev and you should lose the ev or be close to it, so ev only and no sd, and so on
and sd has no meaning for most and never will, it is the public perception and it keeps all math easy, so says the experts too.
Your SD for bankroll ruin is Ok but ruin is actually about 2X that of 60 bets (using $300 bankroll)
this is easy to calculate btw in Excel, as I love Markov chains
but a quick sim shows this also
Simulation of Craps Pass Line Wagers
Odds Multiplier . . . . = 3x, 4x, 5x
Session Bankroll . . . = 60.00
Session will not quit at any win goal
Max. Decisions to quit = 60
No. Sessions simulated = 1000000
Starting Random seed . = 4321017
------------------------------------
All bets are a single unit
------------------------------------
Simulation Results per Session
------------------------------------
Avg. No. games played . = 58.35
Avg. No. games won . . = 28.77
Avg. No. games lost . . = 29.59
Avg. No. dice rolls . . = 196.99
Avg. Total amount bet . = 58.35
Avg. amount bet on Odds = 160.43
Bankroll was busted . . = 9.963% of the time ( 99630) <<<< abouts 2X 5% (neat)
Win goal was met . . . = 0.000% of the time ( 0)
Bankroll decreased . . = 50.698% of the time
Bankroll increased . . = 48.254% of the time
it (sd for ruin) works because 60 is a lot of bets (yes) with 345x odds and the distribution is quite normal looking too
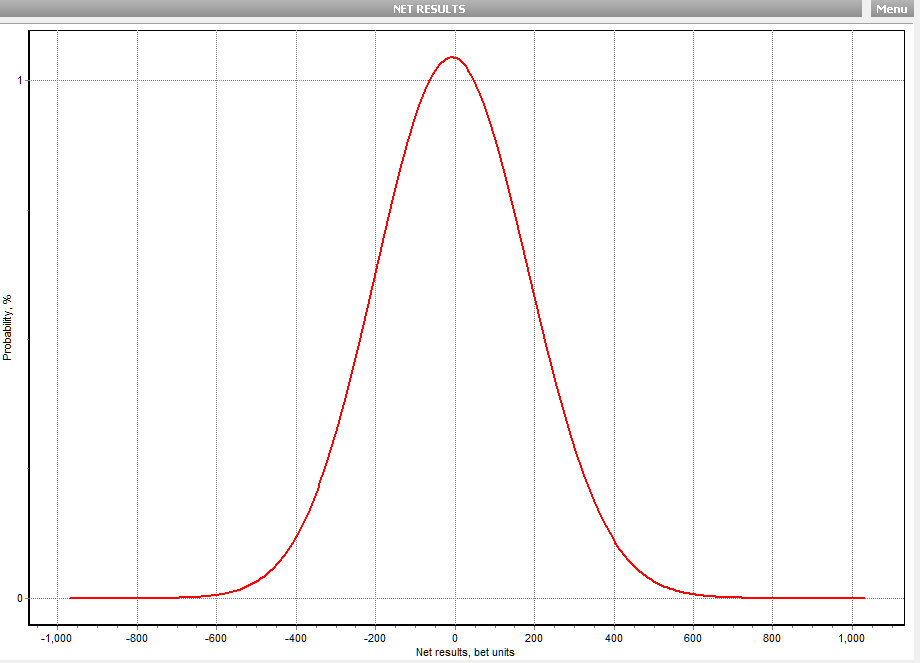
here is 3 bets (what a mess)

how about 6 bets
Oh, looks like the shape is showing to be normal too

happy BDay
Sally
Quote: mustangsally
happy BDay
Sally
Good stuff, Mustang Sally, and thanks. Unfortunately, I am sick and not going anywhere, which is why I was posting here on my birthday.
Cheers,
Alan Shank
Quote: goatcabinNo, the difference from the ev is for each possible outcome, as shown in that example.
Once again, it's the outcomes (and their differences from the ev) that are weighted by their probabilities.
That's exactly what the standard deviation is good for. Suppose you are going to play $5 pass with 3, 4, 5x odds for 60 bets. The ev is about -$4 and the SD is $190. 95% chance corresponds to about 1.6 standard deviations (on one tail); 1.6 x $190 is $304, so $300-$325 in starting bankroll would give you about a 95% chance of your bankroll lasting 6 bets.
But the whole concept of confidence intervals is based on standard deviation!
Cheers,
Alan Shank
Oh my!
Well . . . good luck to you!


